Казахский Университет Международных Отношений и Мировых Языков СРС

Казахский Университет Международных Отношений и Мировых Языков СРС На тему: Законы Булевой алгебры и упрощение логических выражений Выполнила: студентка факультета Востоковедения; китайский язык; р/о; 114 гр Абдурахманова К.

Содержание. 1. Историческая справка. 2. Булева алгебра. 3 Логические выражения. 3. 1 Логическое отрицание. 3. 2 Логическое сложение. 3. 3 Логическое умножение. 3. 4 Логическое следование. 3. 5 Эквивалентность. 4. Упрощение лог. выр-ий.

Историческая справка. Немецкий ученый Лейбниц первым (в 1666 году) попытался перевести законы мышления (формальную логику) из словесного царства, полного неопределенностей, в царство математики, где отношения между объектами или высказываниями определяются в виде математических соотношений. Уже после смерти Лейбница В 1847 году Буль написал важную статью на тему «Математический анализ логики» , а в 1854 году развил свои идеи в работе «Исследование законов мышления» .

Буль изобрёл своеобразную алгебру – систему обозначений и правил, применимую ко всевозможным объектам, от чисел и букв до предложений. Основополагающим законом булевой алгебры является то что логические переменные могут принимать только два значения { «да» , «нет» }, { «истинно» , «ложно» } и т. д. Переменные обычно обозначаются, как и двоичные цифры, символами 0 и 1.

Булева функция может быть задана: n n n n словесным описанием таблицей истинности формулой, состоящей из букв, знаков логических операций и скобок координатным способом (картой Карно) диаграммой Венна геометрическим способом (гиперкубами) диаграммой двоичного решения

Логические выражения 1. Логические 2. Предикаты. утверждения – это конкретные частные утверждения, заведомо истинные или ложные. иначе говоря, это логические переменые.

Способы задания булевых функций n Матричный способ При матричном способе булева функция f(x 1, . . . , xn) задается таблицей истинности, в левой части которой представлены все возможные двоичные наборы длины n, а в правой указывается значение функции на этих наборах.

Способы задания булевых функций n Геометрический способ При геометрическом способе булева функция f(х1, . . . , xn) задается с помощью n-мерного куба. Отмечая точками вершины куба, в которых функция принимает единичные (либо нулевые) значения, получим геометрическое представление функции. а) n=1 б) n=2 в) n=3 Рисунок 1 - Геометрическое задание булевой функции: а) одной переменной: б) двух переменных; в) трех переменных.

Способы задания булевых функций n Аналитический способ При аналитическом способе булева функция задается формулами, т. е. аналитическими выражениями, построенными на основе операций булевой алгебры. Аналитический способ задания булевых функций занимает особое место в проектировании цифровых автоматов

Логическое отрицание. Логическое отрицание или Инверсия, определяется над одним аргументом (простым или сложным логическим выражением) следующим образом: если исходное выражение истинно, то результат его отрицания будет ложным, и наоборот. Операция означает, что к исходному логическому выражению добавляют частицу НЕ или слова НЕВЕРНО, ЧТО. Обозначается значком А 0 1 ┐А 1 0

Логическое сложение. Логическое сложение или Дизъюнкция, определяет логическое соединение двух логических выражений (высказываний) с помощью союза ИЛИ. Обозначается значком ۷ Сложное логическое выражение будет истинным тогда и только тогда, когда истинно хотя бы одно из исходных (простых) логических выражений. А В А۷ В ☺ запомни знак! Пример: для сдачи экзамена необходимы знания или везение. 0 0 1 1 1 0 1

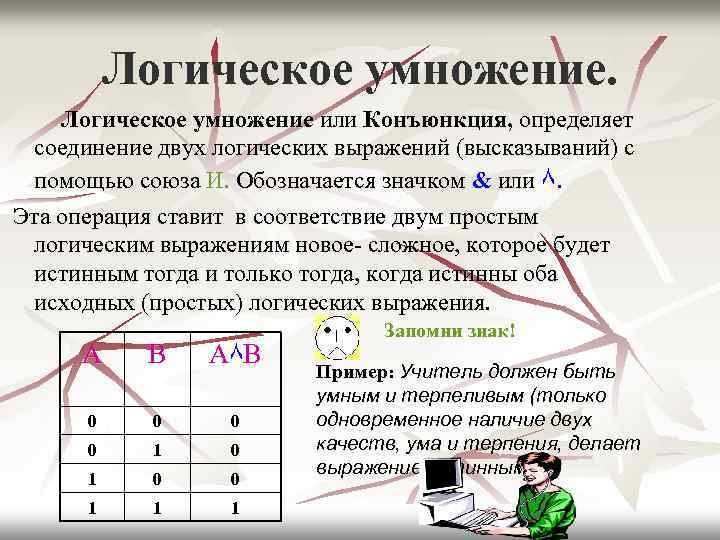Логическое умножение или Конъюнкция, определяет соединение двух логических выражений (высказываний) с помощью союза И. Обозначается значком & или ٨. Эта операция ставит в соответствие двум простым логическим выражениям новое- сложное, которое будет истинным тогда и только тогда, когда истинны оба исходных (простых) логических выражения. А В А٨ В 0 0 1 1 1 Запомни знак! Пример: Учитель должен быть умным и терпеливым (только одновременное наличие двух качеств, ума и терпения, делает выражение истинным).

Логическое следование или Импликация. Эта операция связывает два простых логических выражения, из которых первое является условием, а второе- следствием из этого условия. Выражается словами ЕСЛИ…, ТО… Обозначается значком Результатом импликации является ложь тогда и только тогда, когда (А) истинно, а следствие (В) ложно. А В 0 0 1 1 1 Например: Если выучишь материал, то сдашь зачет (высказывание ложно только тогда, когда материал выучен, а зачет не сдан, ведь сдать зачет можно и случайно, например если попался единственный знакомый вопрос или удалось воспользоваться шпаргалкой.

Эквивалентность или Равнозначность. Определяет результат сравнения двух простых логических выражений А и В, обозначается значком Результат – новое логическое выражение, которое является истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны. А В 0 0 1 0 1 0 0 1 1 1 Пример: Когда в зимний день светит солнце и «кусает» мороз, это значит, что атмосферное давление высокое.

Порядок выполнения логических операций. 1. Инверсия - ┐ 2. Конъюнкция - & или ٨ 3. Дизъюнкция – ۷ 4. Импликация – 5. Эквивалентность - Для изменения указанного порядка выполнения логических операций используются круглые скобки. Например: А ^ В v ¬ (А v В)

Упрощение логических выражений n n Привести правую часть равенства к левой, или наоборот; Привести обе части равенства к единому выражению. Эти действия называются преобразованием. Если в результате преобразования уменьшилось количество операций, то говорят об упрощении. И преобразования и упрощения осуществляются на основе разобранных на уроке законов логики

Упрощение логических выражений Пример: (Для наглядности можно заменить операции логического сложения и умножения знаками «+» и «*» ) (А v ¬ В ) ^ (¬ А v В) = (А + ¬ В) * (¬ А + В) n

Последовательно выполним действия: n Раскрываем скобки по распределительному закону: А ^ (¬ А) v А ^ В v (¬ В) ^ (¬ А) v (¬ В) ^ В; n Заменяем А ^ (¬ А) на 0 по закону противоречия; n Заменяем (¬ В) ^ В на 0 по закону противоречия; n Заменяем (¬ В) ^ (¬ А) на ¬ (А v В) по закону де Моргана и получаем выражение, содержащее 4 простые операции. А ^ В v ¬ (А v В)

Основные законы логики. 1. Отсутствие степеней и коэффициентов (идемпотентность): А ٨ А= А; А ۷ А= А 2. Двойное отрицание (инволюция): ¬(¬А) = А 3. Закон исключения третьего: А۷¬ А=1(всегда истина) 4. Закон противоречия: А ٨ ¬ А= 0 (всегда ложь) 5. Независимость от перестановки мест (коммутативность): А۷ В= В ۷ А; А ٨ В = В ٨ А 6. Независимость от порядка выполнения однотипных действий (ассоциативность): (А۷В) ۷ С = А ۷ (В۷С); (А٨В) ٨ С = А ٨ (В٨С).

7. Дистрибутивность (распределение): Умножения(А۷В) ٨ С = (А٨С) ۷ (В٨С) и наоборот: (А٨В) ۷ (В٨С) = В ٨ (А۷С). Сложения- А۷В٨С = (А۷В) ٨ (А۷С). 8. Законы де Моргана: а) Отрицание одновременной истинности: ¬(А٨В)= ¬А۷¬В б) Отрицание вариантов: ¬ (А۷В) = ¬А ٨¬В

а) Отрицание одновременной истинности: ¬(А٨В)= ¬А۷¬В А В ¬(А٨В) ¬А۷¬ В 0 0 0 1 1 1 1 0 1 0 б) Отрицание вариантов: ¬ (А۷В) = ¬А ٨¬В А В ¬ (А۷В) ¬А٨¬ В 0 0 0 1 1 0 1 0 0

Какое логическое выражение равносильно выражению ¬ (A / B) / ¬C? ¬A / B / ¬C n (¬A / ¬B) / C n ¬A / ¬B / ¬C Применим закон де Моргана. ¬ (A / B) = ¬A / ¬B Раскрывая скобки получаем n (¬A / ¬B) / ¬C = (¬A / ¬B) / ¬C Ответ: верный ответ № 2