Казанский Приволжский федеральный университет СОВРЕМЕННЫЕ ТЕОРИИ ХИМИЧЕСКОЙ СВЯЗИ

Казанский (Приволжский) федеральный университет СОВРЕМЕННЫЕ ТЕОРИИ ХИМИЧЕСКОЙ СВЯЗИ Теория симметрии в применении к проблемам химической связи: Геометрический подход Казань - 2013

2

3 Понятие симметрии

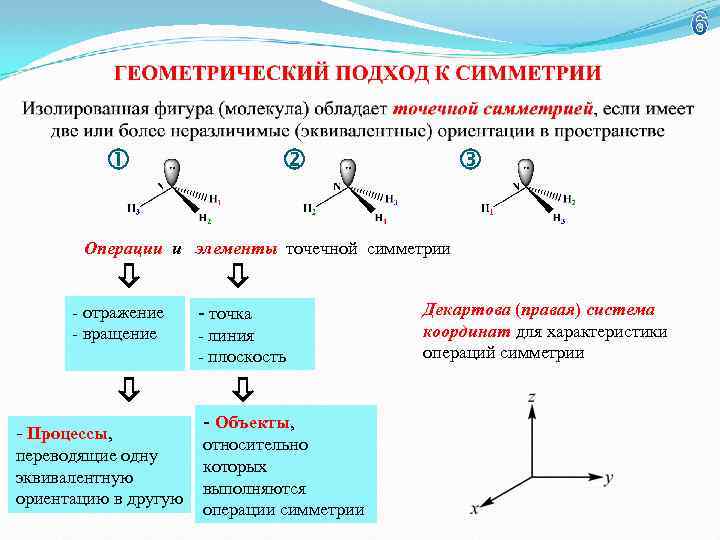6 Операции и элементы точечной симметрии - отражение - вращение - Процессы, переводящие одну эквивалентную ориентацию в другую - точка - линия - плоскость - Объекты, относительно которых выполняются операции симметрии Декартова (правая) система координат для характеристики операций симметрии

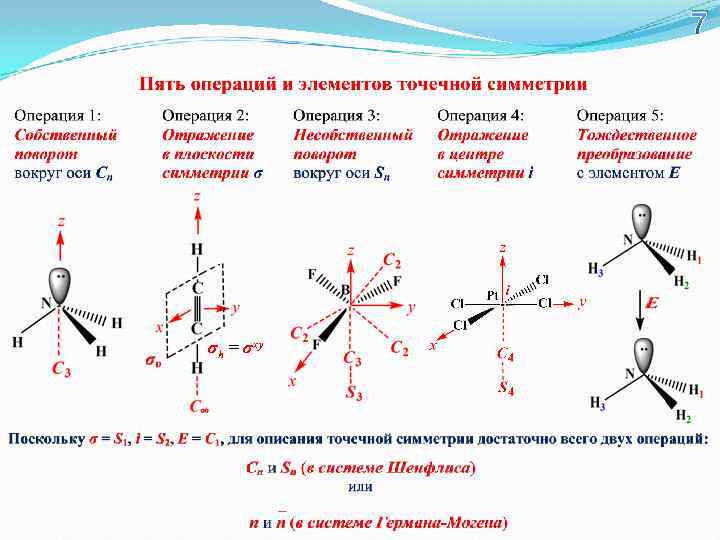7 σh = σxy

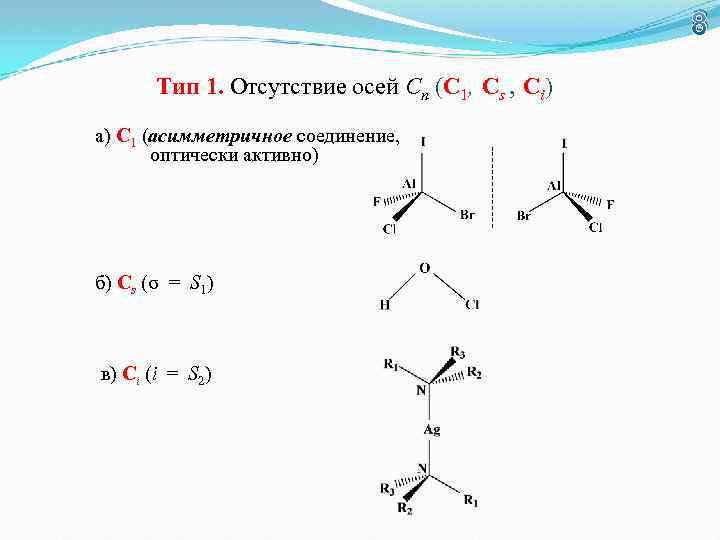8 Тип 1. Отсутствие осей Сn (С 1, Сs , Сi) а) С 1 (асимметричное соединение, оптически активно) б) Сs (σ = S 1) в) Сi (i = S 2)

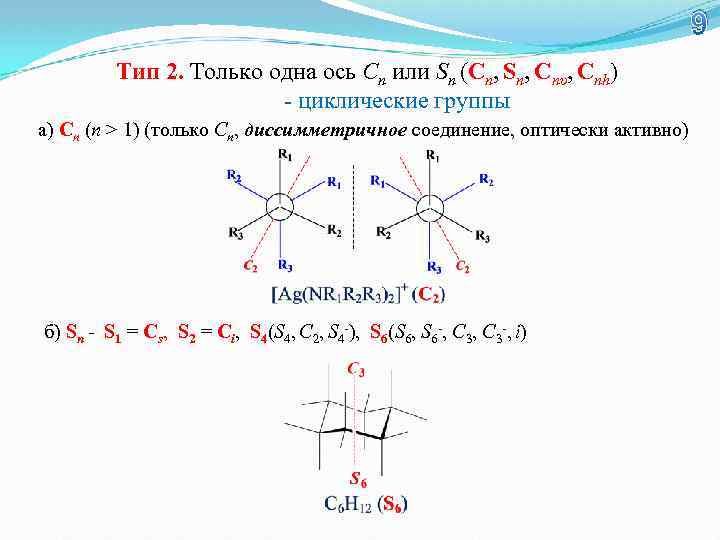9 Тип 2. Только одна ось Сn или Sn (Сn, Sn, Сnυ, Сnh) - циклические группы а) Сn (n > 1) (только Сn, дисcимметричное соединение, оптически активно) б) Sn - S 1 = Cs, S 2 = Сi, S 4(S 4, C 2, S 4 -), S 6(S 6, S 6 -, C 3 -, i)

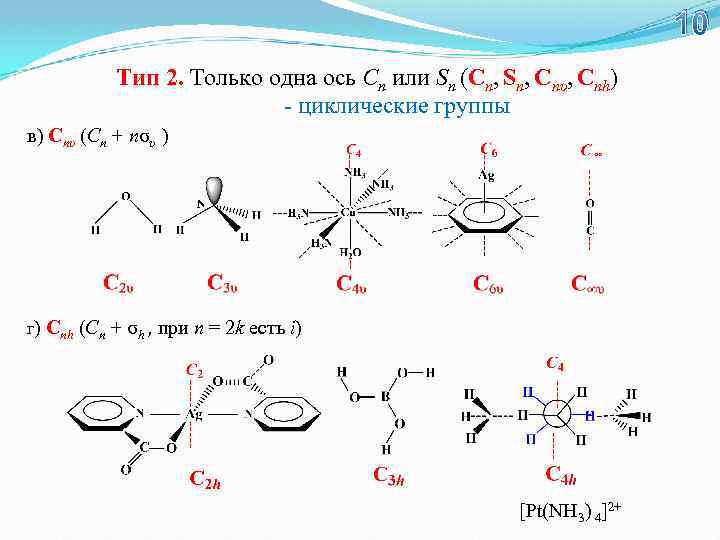10 Тип 2. Только одна ось Сn или Sn (Сn, Sn, Сnυ, Сnh) - циклические группы в) Сnυ (Cn + nσυ ) г) Сnh (Cn + σh , при n = 2 k есть i) [Pt(NH 3) 4]2+

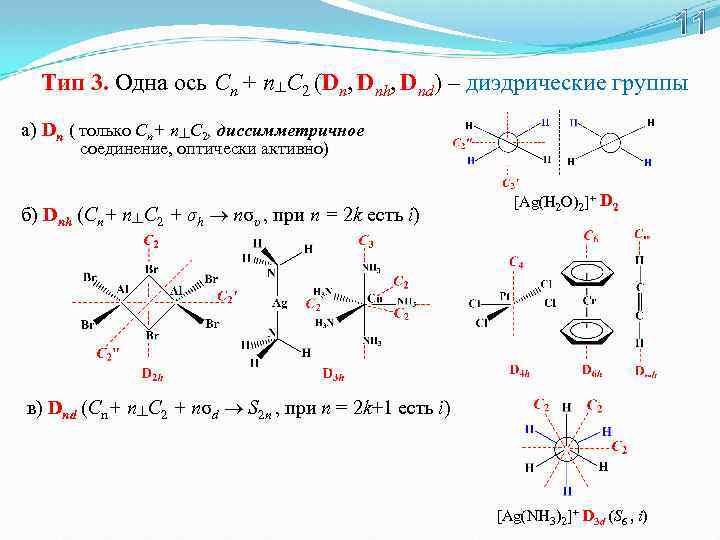11 Тип 3. Oдна ось Cn + n┴С 2 (Dn, Dnh, Dnd) – диэдрические группы а) Dn ( только Cn+ n┴С 2, диссимметричное соединение, оптически активно) б) Dnh (Cn+ n┴С 2 + σh nσυ , при n = 2 k есть i) [Ag(Н 2 О)2]+ D 2 в) Dnd (Cn+ n┴С 2 + nσd S 2 n , при n = 2 k+1 есть i) [Ag(NН 3)2]+ D 3 d (S 6 , i)

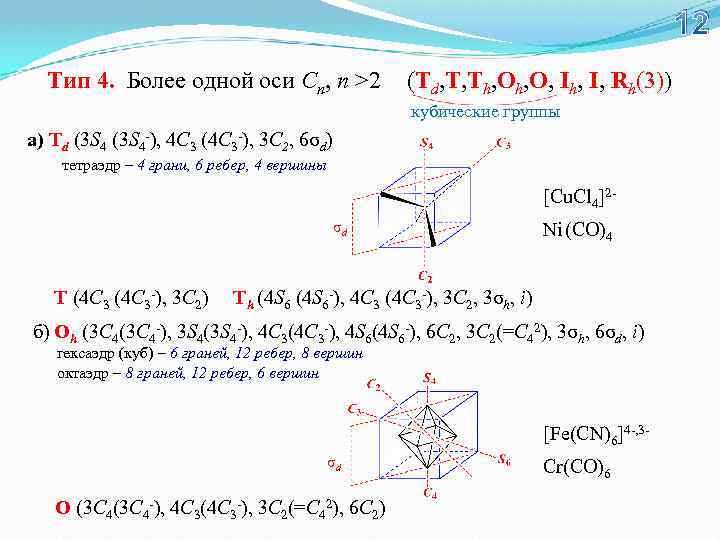12 Тип 4. Более одной оси Сn, n >2 (Td, T, Th, O, Ih, I, Rh(3)) кубические группы а) Td (3 S 4 -), 4 C 3 (4 C 3 -), 3 C 2, 6σd) тетраэдр – 4 грани, 6 ребер, 4 вершины [Cu. Cl 4]2σd T (4 C 3 -), 3 C 2) Ni (CO)4 Th (4 S 6 -), 4 C 3 (4 C 3 -), 3 C 2, 3σh, i) б) Oh (3 C 4 -), 3 S 4(3 S 4 -), 4 C 3(4 C 3 -), 4 S 6(4 S 6 -), 6 C 2, 3 C 2(=C 42), 3σh, 6σd, i) гексаэдр (куб) – 6 граней, 12 ребер, 8 вершин октаэдр – 8 граней, 12 ребер, 6 вершин [Fe(CN)6]4 -, 3σd O (3 C 4 -), 4 C 3(4 C 3 -), 3 C 2(=C 42), 6 C 2) Cr(CO)6

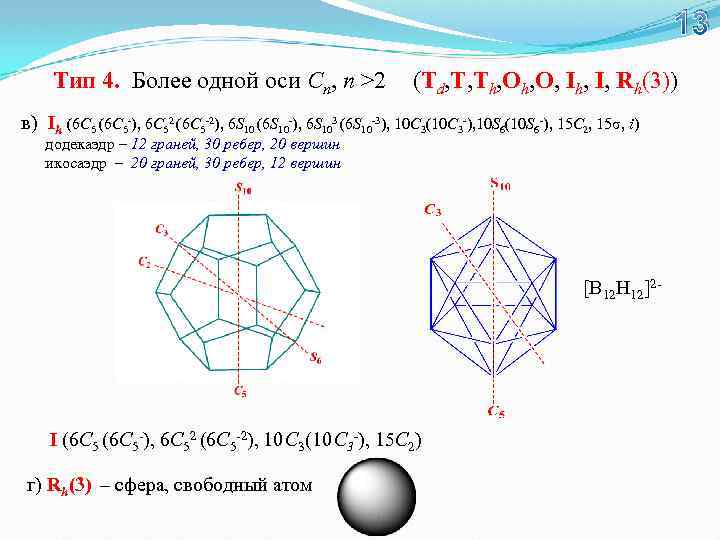13 Тип 4. Более одной оси Сn, n >2 (Td, T, Th, O, Ih, I, Rh(3)) в) Ih (6 C 5 -), 6 C 52 (6 C 5 -2), 6 S 10 (6 S 10 -), 6 S 103 (6 S 10 -3), 10 C 3(10 C 3 -), 10 S 6(10 S 6 -), 15 C 2, 15σ, i) додекаэдр – 12 граней, 30 ребер, 20 вершин икосаэдр – 20 граней, 30 ребер, 12 вершин [B 12 H 12]2 - I (6 C 5 -), 6 C 52 (6 C 5 -2), 10 C 3(10 C 3 -), 15 C 2) г) Rh(3) – сфера, свободный атом

14 Архимедовы и каталановы тела (1)

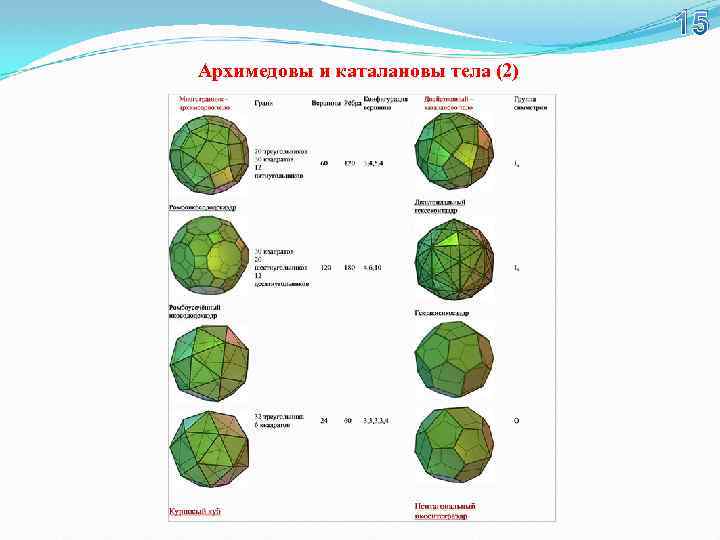15 Архимедовы и каталановы тела (2)

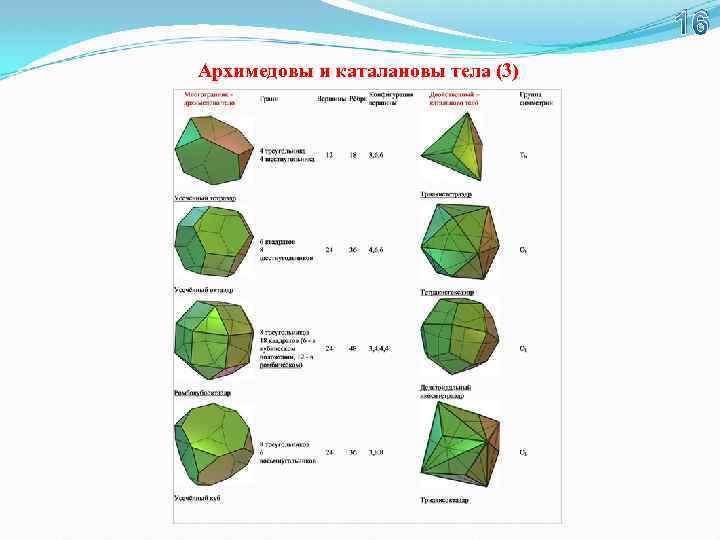16 Архимедовы и каталановы тела (3)

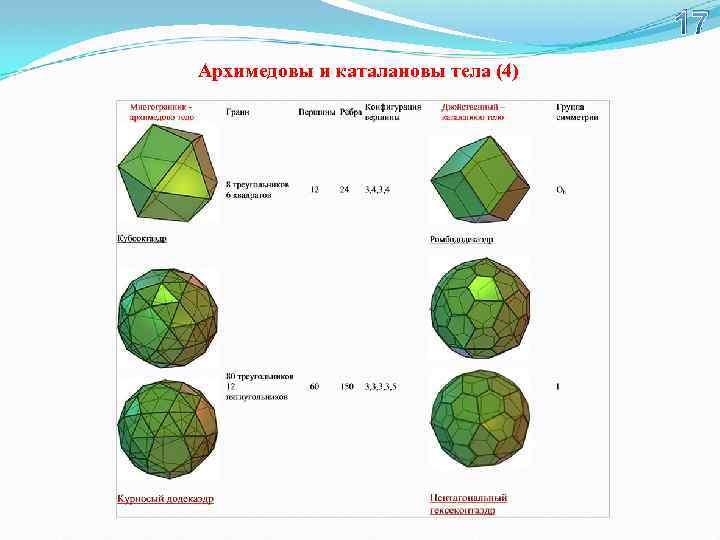17 Архимедовы и каталановы тела (4)

18 Некоторые проблемы строения молекул, решаемые геометрическим подходом к теории симметрии