Канонические уравнения частных видов движения плоскости Введем

Канонические уравнения частных видов движения плоскости

Введем на плоскости прямоугольную декартовую систему координат Oxy: O – начала координат, - единичные точки. 1. Параллельный перенос Пусть - параллельный перенос, определяемый вектором - произвольная точка плоскости, данном параллельном переносе. - ее образ при ,

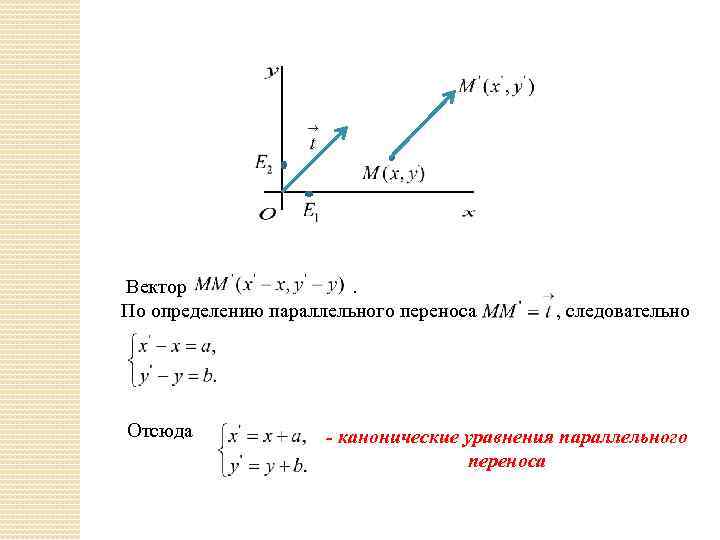Вектор. По определению параллельного переноса Отсюда , следовательно - канонические уравнения параллельного переноса

2. Симметрия относительно прямой Пусть - симметрия плоскости относительно оси - произвольная точка плоскости, ,

Так как точка оси Ox, симметрична точке M (x, y) относительно следовательно она имеет координаты (x, -y). Отсюда - канонические уравнения симметрии относительно прямой

3. Симметрия относительно точки Пусть - произвольная точка плоскости, - точка, симметрическая точке М относительно начала координат О. Так как точка координат, симметрична точке М, относительно начала Следовательно, она имеет координаты (-x, -y). Тогда

4. Поворот Пусть - поворот вокруг начала координат на ориентированный угол , - произвольная точка плоскости, - ее образ при данном повороте. Обозначим через - угол между Ox и OM. Тогда или .

Обозначим длину отрезка ОМ через r. Тогда: Итак, - канонические уравнения поворота