be57904b00b2a0f1da4ae79c1c402b92.ppt
- Количество слайдов: 18
 Kahnemann and Tversky Prospect Theory Economics 328 Spring 2005
Kahnemann and Tversky Prospect Theory Economics 328 Spring 2005
 Basic Definitions n n Definition: Imagine a situation with many possible outcomes where the outcome is determined randomly. We refer to this situation as a gamble or a lottery. We refer to the list of possible outcomes as events. Suppose we were able to repeat the gamble an infinite number of times. The frequency with which an event occurs is its probability. Example: Suppose I have a bingo cage with 60 red balls and 40 green balls in it. I draw one ball from the bingo cage at random. What are the possible events? What is the probability of each event? Events = {Red, Green} p(Red) = 60/100 =. 6 p(Green) = 40/100 =. 4
Basic Definitions n n Definition: Imagine a situation with many possible outcomes where the outcome is determined randomly. We refer to this situation as a gamble or a lottery. We refer to the list of possible outcomes as events. Suppose we were able to repeat the gamble an infinite number of times. The frequency with which an event occurs is its probability. Example: Suppose I have a bingo cage with 60 red balls and 40 green balls in it. I draw one ball from the bingo cage at random. What are the possible events? What is the probability of each event? Events = {Red, Green} p(Red) = 60/100 =. 6 p(Green) = 40/100 =. 4
 Expected Value n n Definition: Suppose we associate a monetary payoff with each possible event in a gamble. The expected value of the gamble is the weighted average of the payoffs where the weight for each event is its probability. More formally, let there be n events, let pi be the probability of event i, and let i be the payoff associated with event i. The following formula gives the expected value of the gamble. Example: Continuing the previous example, suppose you earn $3 if a red ball is drawn and $1 if a green ball is drawn. What is the expected value of the gamble?
Expected Value n n Definition: Suppose we associate a monetary payoff with each possible event in a gamble. The expected value of the gamble is the weighted average of the payoffs where the weight for each event is its probability. More formally, let there be n events, let pi be the probability of event i, and let i be the payoff associated with event i. The following formula gives the expected value of the gamble. Example: Continuing the previous example, suppose you earn $3 if a red ball is drawn and $1 if a green ball is drawn. What is the expected value of the gamble?
 Expected Utility n n Definition: Suppose we consider an individual as having a utility function over possible payoffs from a gamble, u( ). (Technically, we consider a utility function over wealth. Why is the distinction important and what does it imply about individuals’ decision making? ) The expected utility of a gamble is the expected value of the utility. Definition: We say that an individual whose marginal utility of wealth decreases as his/her wealth rises has decreasing marginal utility from wealth. If an individual strictly prefers a sure thing to a gamble with the same expected value, we call this individual risk adverse. If an individual has decreasing marginal utility from wealth and maximizes his/her expected utility, he/she must be risk adverse.
Expected Utility n n Definition: Suppose we consider an individual as having a utility function over possible payoffs from a gamble, u( ). (Technically, we consider a utility function over wealth. Why is the distinction important and what does it imply about individuals’ decision making? ) The expected utility of a gamble is the expected value of the utility. Definition: We say that an individual whose marginal utility of wealth decreases as his/her wealth rises has decreasing marginal utility from wealth. If an individual strictly prefers a sure thing to a gamble with the same expected value, we call this individual risk adverse. If an individual has decreasing marginal utility from wealth and maximizes his/her expected utility, he/she must be risk adverse.
 Expected Utility Example n Example: Suppose I offer you the choice between the following two gambles: Gamble A: 100% Gamble B: n Win $240 Win $400 Win $100 50% Show that an expected value maximizer will choose Gamble B. Show that an expected utility maximizer with u( ) = 1/2 will choose Gamble A. EVA = 240
Expected Utility Example n Example: Suppose I offer you the choice between the following two gambles: Gamble A: 100% Gamble B: n Win $240 Win $400 Win $100 50% Show that an expected value maximizer will choose Gamble B. Show that an expected utility maximizer with u( ) = 1/2 will choose Gamble A. EVA = 240
 Kahnemann and Tversky Prospect Theory (1979) n Research Questions n Expected utility theory embodies a number of strong assumptions. n n Expected utility is linear in probabilities Preferences are over wealth (asset integration) rather than gains and losses. Kahnemann and Tversky aim to illustrate a number of violations of expected utility theory and to develop a set of empirical regularities that inform the development of prospect theory. Initial Hypotheses n n Kahnemann and Tversky expected for find strong violations of EUT. Kahnemann and Tversky also expected to find a series of empirical regularities in the data. n n n certainty effects reflection effects isolation effects
Kahnemann and Tversky Prospect Theory (1979) n Research Questions n Expected utility theory embodies a number of strong assumptions. n n Expected utility is linear in probabilities Preferences are over wealth (asset integration) rather than gains and losses. Kahnemann and Tversky aim to illustrate a number of violations of expected utility theory and to develop a set of empirical regularities that inform the development of prospect theory. Initial Hypotheses n n Kahnemann and Tversky expected for find strong violations of EUT. Kahnemann and Tversky also expected to find a series of empirical regularities in the data. n n n certainty effects reflection effects isolation effects
 Kahnemann and Tversky Prospect Theory (1979) n n Experimental Design: The experiments reported in this paper rely on a series of hypothetical questions asked to Israeli students. In each problem, the students were asked to choose between two pairs of gambles. Their choices over the various pairs are then used to generate violations. Methodological Questions n n n Are results generated without monetary payoffs as reliable as results with real payoffs? Does the magnitude of the (hypothetical) stakes play a large role in generating the results? Without any method of pricing the gambles, how large are the violations?
Kahnemann and Tversky Prospect Theory (1979) n n Experimental Design: The experiments reported in this paper rely on a series of hypothetical questions asked to Israeli students. In each problem, the students were asked to choose between two pairs of gambles. Their choices over the various pairs are then used to generate violations. Methodological Questions n n n Are results generated without monetary payoffs as reliable as results with real payoffs? Does the magnitude of the (hypothetical) stakes play a large role in generating the results? Without any method of pricing the gambles, how large are the violations?
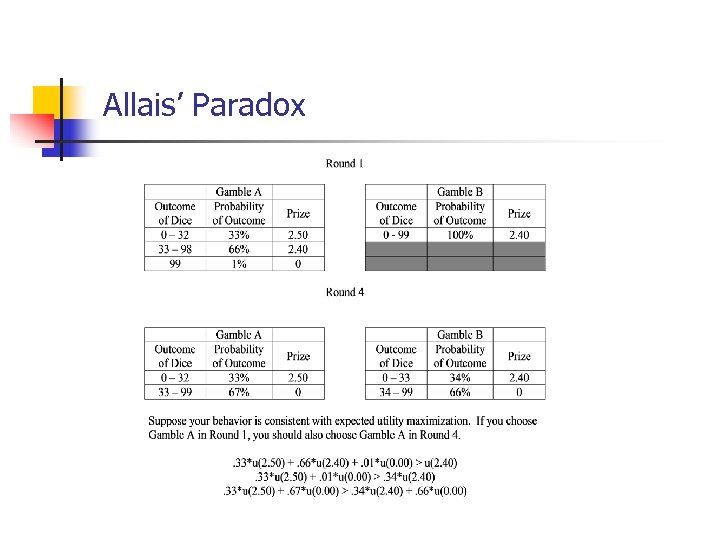 Allais’ Paradox
Allais’ Paradox
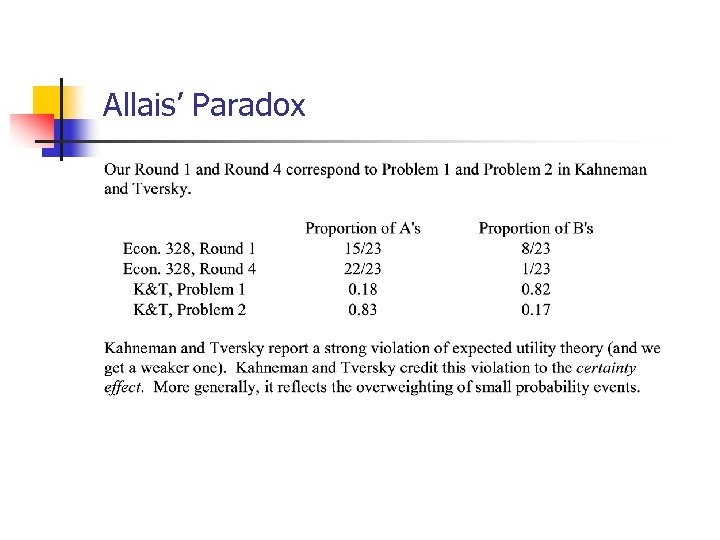 Allais’ Paradox
Allais’ Paradox
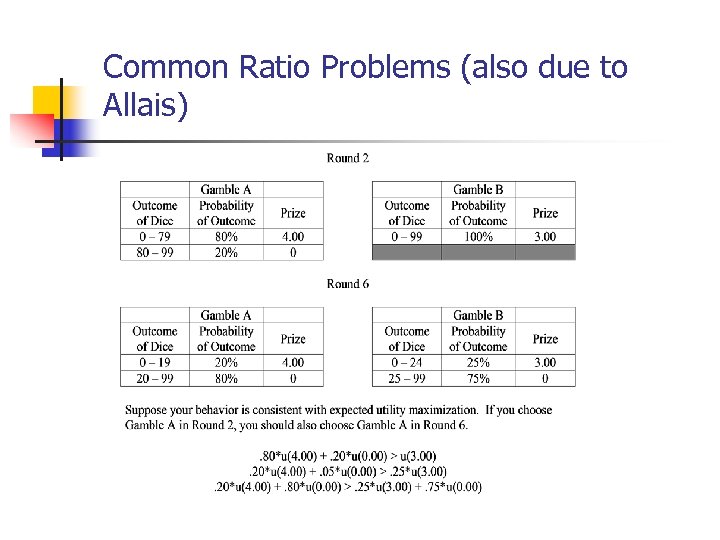 Common Ratio Problems (also due to Allais)
Common Ratio Problems (also due to Allais)
 Common Ratio Problems (also due to Allais)
Common Ratio Problems (also due to Allais)
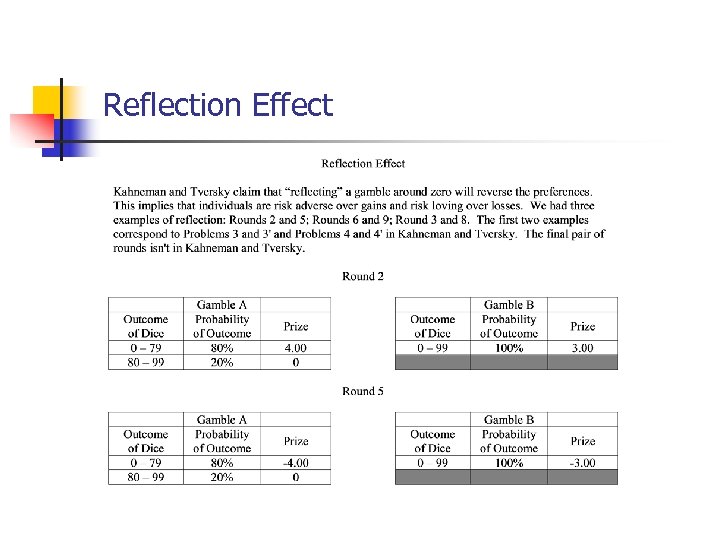 Reflection Effect
Reflection Effect
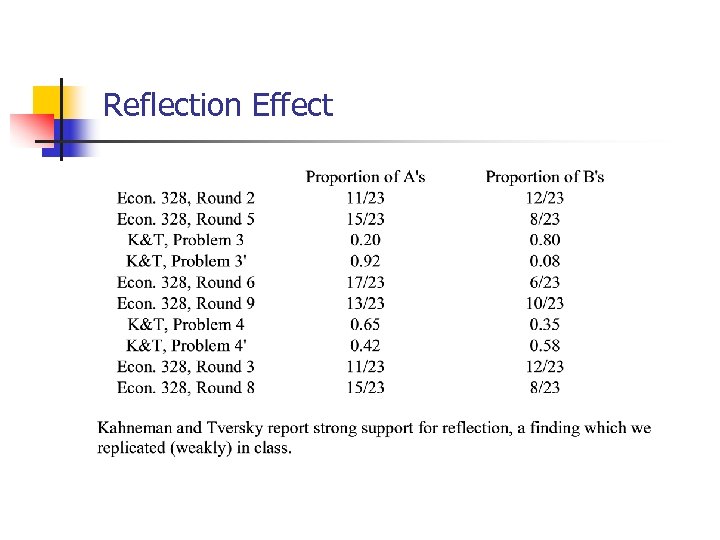 Reflection Effect
Reflection Effect
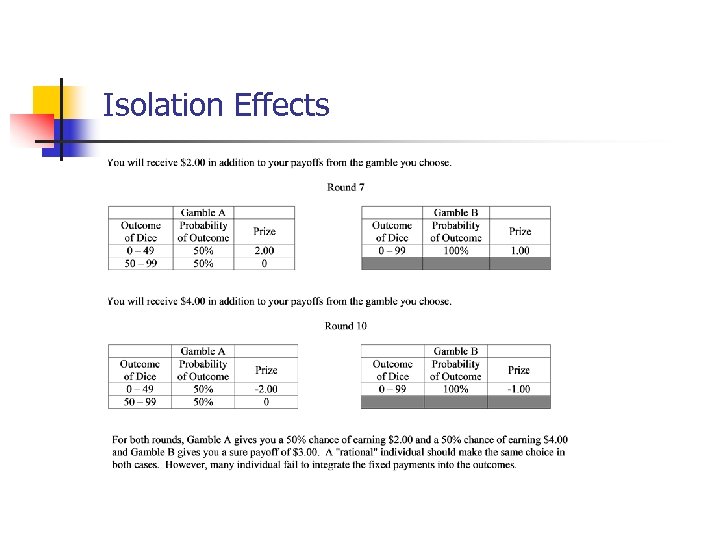 Isolation Effects
Isolation Effects
 Isolation Effects
Isolation Effects
 The Theory of Prospect Theory n Editing Phase n Coding: Outcomes are coded as gains or losses. The reference point can be sensitive to presentation effects and expectations of the decision maker. n Combination: Prospects with identical outcomes can be combined. n Segregation: In some cases, the riskless proportion will be ignored is decision making. n Cancellation: Common components will be discarded in the editing phase. This drives many isolation effects.
The Theory of Prospect Theory n Editing Phase n Coding: Outcomes are coded as gains or losses. The reference point can be sensitive to presentation effects and expectations of the decision maker. n Combination: Prospects with identical outcomes can be combined. n Segregation: In some cases, the riskless proportion will be ignored is decision making. n Cancellation: Common components will be discarded in the editing phase. This drives many isolation effects.
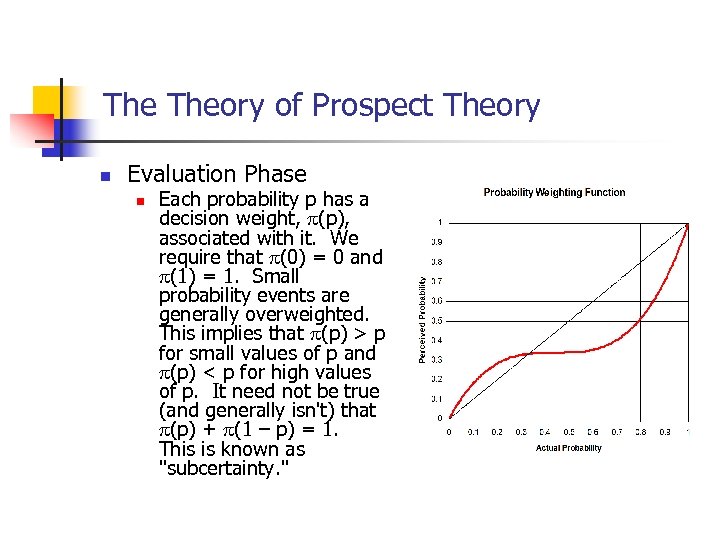 The Theory of Prospect Theory n Evaluation Phase n Each probability p has a decision weight, (p), associated with it. We require that (0) = 0 and (1) = 1. Small probability events are generally overweighted. This implies that (p) > p for small values of p and (p) < p for high values of p. It need not be true (and generally isn't) that (p) + (1 – p) = 1. This is known as "subcertainty. "
The Theory of Prospect Theory n Evaluation Phase n Each probability p has a decision weight, (p), associated with it. We require that (0) = 0 and (1) = 1. Small probability events are generally overweighted. This implies that (p) > p for small values of p and (p) < p for high values of p. It need not be true (and generally isn't) that (p) + (1 – p) = 1. This is known as "subcertainty. "
 The Theory of Prospect Theory n Evaluation Phase n n The outcome is evaluated via a "value function. " This serves much the same role as a utility function. The value function is generally concave for gains and convex for losses. This gives us reflection – risk aversion over gains and risk loving over losses. The value function is steeper for losses than for gains, giving us "loss aversion. " The overall value of a gamble is given by the following equation for a "regular prospect. " In spite of its apparent similarity to expected utility, this differs from expected utility in how probabilities are handles and how outcomes are valued.
The Theory of Prospect Theory n Evaluation Phase n n The outcome is evaluated via a "value function. " This serves much the same role as a utility function. The value function is generally concave for gains and convex for losses. This gives us reflection – risk aversion over gains and risk loving over losses. The value function is steeper for losses than for gains, giving us "loss aversion. " The overall value of a gamble is given by the following equation for a "regular prospect. " In spite of its apparent similarity to expected utility, this differs from expected utility in how probabilities are handles and how outcomes are valued.


