Кафедра холодильных машин и низкопотенциальной энергетики Машины низкотемпературной

Скачать презентацию Кафедра холодильных машин и низкопотенциальной энергетики Машины низкотемпературной

Маш.низкотемп. техн_часть_2.ppt

Количество слайдов: 174

Кафедра холодильных машин и низкопотенциальной энергетики Машины низкотемпературной техники часть 2 1. 2. 2. 3. Учебная литература Холодильные машины Учебник под ред. Тимофеевского Л. С. СПб. : «Политехника» , 1997. 992 с. Холодильные машины Учебник под ред. Тимофеевского Л. С. СПб. : «Политехника» , 2006. 944 с. 3. Тепловые и конструктивные расчёты холодильных машин. Учебное пособие под ред. Сакуна И. А. - Л. : Машиностроение, 1987. 423 с. Машины низкотемпературной техники часть 2 1 26. 12. 06

Холодильные компрессоры динамического принципа действия Преимущества перед объёмными компрессорами : 1. Меньшие габариты и масса. 2. Высокая надёжность в работе. 3. Практически полная уравновешенность. 4. Равномерность подачи сжатого вещества. 5. Отсутствие загрязнения вещества смазочным маслом. 6. Возможность получения значительно более высокой производительности. 7. Возможность непосредственного соединения с высокооборотным приводным двигателем Машины низкотемпературной техники часть 2 2 26. 12. 06

Недостатки динамических компрессоров : 1. Трудность выполнения эффективных компрессоров малой производительности. 2. Узкий диапазон устойчивой работы. 3. Трудность получения высоких отношений давления. 4. Зависимость характеристик от термодинамических свойств рабочего вещества. Машины низкотемпературной техники часть 2 3 26. 12. 06

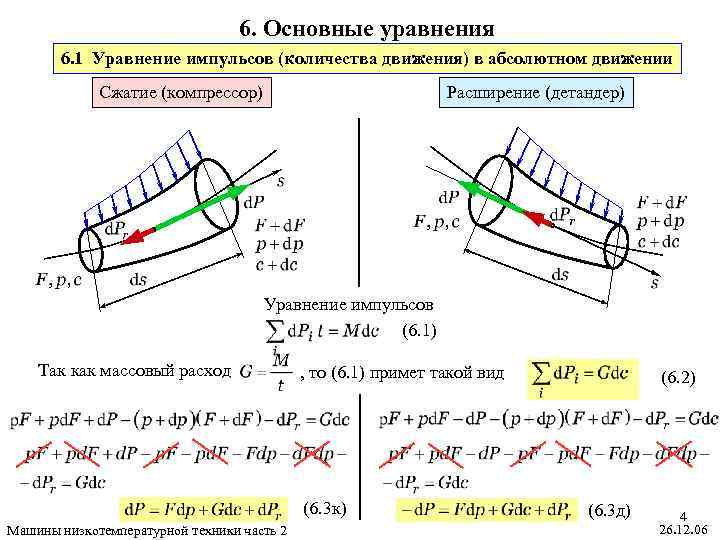6. Основные уравнения 6. 1 Уравнение импульсов (количества движения) в абсолютном движении Сжатие (компрессор) Расширение (детандер) Уравнение импульсов (6. 1) Так как массовый расход , то (6. 1) примет такой вид (6. 3 к) Машины низкотемпературной техники часть 2 (6. 2) (6. 3 д) 4 26. 12. 06

Сжатие (компрессор) Расширение (детандер) Массовый расход После подстановки массового расхода и деления на в обоих случаях находим : (6. 4 к) (6. 4 д) Внешняя сила, действующая на поток вызвана удельной массовой силой , Н/кг. – удельная работа, подведенная к рабочему веществу или отведенная от него. Удельное касательное напряжение трения при движении рабочего вещества (6. 5) Тогда сила сопротивления Удельная работа, затраченная на преодоление сопротивлений – эквивалентный диаметр канала, м. Машины низкотемпературной техники часть 2 5 26. 12. 06

Сжатие (компрессор) В итоге получим : Расширение (детандер) Чтобы не иметь дело с отрицательными значениями работы, множим всё на -1 : (6. 5 к) (6. 5 д) При отсутствии подвода или отвода энергии от потока (изоэнергетическое течение) (6. 6) Изоэнергетическое течение без трения (без потерь) (6. 7) Уравнения (6. 5÷ 6. 7) получены Д. Бернулли и носят его имя. Машины низкотемпературной техники часть 2 6 26. 12. 06

Сжатие (компрессор) Расширение (детандер) После интегрирования (6. 8 к) (6. 8 д) При отсутствии подвода или отвода энергии от потока (изоэнергетическое течение) (6. 9 к) (6. 9 д) Изоэнергетическое течение без трения (без потерь) (6. 10 к) Машины низкотемпературной техники часть 2 (6. 10 д) 7 26. 12. 06

6. 1 Уравнение импульсов (количества движения) в относительном движении Выделенный элемент вращается вместе с колесом и на него действуют кроме сил давления силы : Центробежная сила (6. 11) , ортогональная оси Кориолисова сила Сила сопротивления. Угол потока в относительном движении определяется выражением Сумма проекций сил на ось s (6. 12) Преобразуем левую часть (6. 12) с помощью (6. 11) Подставим уравнение расхода , после чего (6. 12) примет вид (6. 13) Машины низкотемпературной техники часть 2 8 26. 12. 06 .

Разделив обе части равенства на , и заменив , из (6. 13) получим окончательно уравнение импульсов в относительном движении : (6. 13) Сжатие (компрессор) Расширение (детандер) , а при При движении к центру ; чтобы получаемые расширении величины работ были положительны, множим обе части равенства на – 1 и меняем пределы интегрирования Машины низкотемпературной техники часть 2 9 26. 12. 06

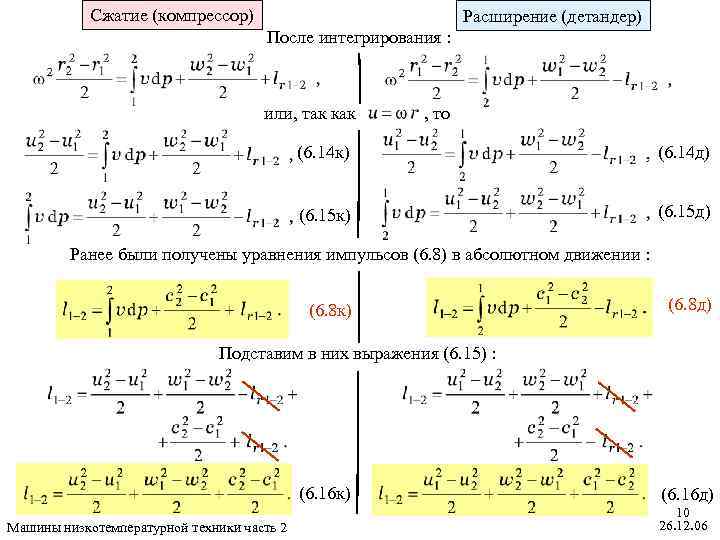Сжатие (компрессор) Расширение (детандер) После интегрирования : или, так как , то (6. 14 к) (6. 14 д) (6. 15 к) (6. 15 д) Ранее были получены уравнения импульсов (6. 8) в абсолютном движении : (6. 8 к) (6. 8 д) Подставим в них выражения (6. 15) : (6. 16 к) Машины низкотемпературной техники часть 2 (6. 16 д) 10 26. 12. 06

Сжатие (компрессор) Расширение (детандер) Без потерь (6. 17 к) (6. 18 к) (6. 17 д) (6. 18 д) Уравнение энергии Уравнение 1 -го закона термодинамики (6. 19) Количество подводимой теплоты Техническая работа (6. 20) Неадиабатные процессы с потерями (6. 21 к) Машины низкотемпературной техники часть 2 (6. 21 д) 11 26. 12. 06

Сжатие (компрессор) Расширение (детандер) (6. 22 к) (6. 23 к) (6. 22 д) (6. 23 д) Адиабатные процессы с потерями (6. 24 к) (6. 25 к) (6. 24 д) (6. 25 д) Адиабатные процессы без потерь (6. 26 к) (6. 26 д) После интегрирования Неадиабатные процессы с потерями (6. 27 к) (6. 27 д) (6. 28 к) (6. 28 д) (6. 29 к) (6. 29 д) Машины низкотемпературной техники часть 2 12 26. 12. 06

Сжатие (компрессор) Расширение (детандер) Адиабатные процессы с потерями (6. 30 к) (6. 30 д) (6. 31 к) (6. 31 д) (6. 32 к) (6. 32 д) Адиабатные процессы без потерь (6. 33 к) (6. 33 д) (6. 34 к) (6. 34 д) Адиабатные процессы без потерь, или внутренне обратимые адиабатные процессы – это изоэнтропные процессы Машины низкотемпературной техники часть 2 13 26. 12. 06

Уравнение состояния Идеальный газ (6. 35) (6. 36) Реальный газ (6. 37) (6. 38) Уравнение Боголюбова-Майера. (6. 39) Метод условных температур Произведение коэффициента сжимаемости и температуры объединяются в один комплекс, называемый условной температурой : (6. 40) После этого уравнение состояния принимает форму уравнения идеального газа (6. 41) (6. 42) Газ, подчиняющийся уравнению (1. 32), называется идеализированным газом. Машины низкотемпературной техники часть 2 14 26. 12. 06

У идеального газа – полный дифференциал, а энтропия – функция состояния. При этом не является функцией состояния и не является полным дифференциалом, так количество теплоты, подводимой к газу, зависит от характера процесса. Термодинамическая температура является интегрирующим делителем количества теплоты. У идеализированного газа будет полным дифференциалом, если . Это значит, что вдоль линий будет и. В идеализированном газе ( «идеальном паре» по определению В. Траупеля) будет : и все параметры можно определять по зависимостям, полученным для идеального газа с заменой термодинамической температуры на условную температуру. Это позволяет упростить расчёты и использовать весь математический аппарат газодинамических функций. 15 Машины низкотемпературной техники часть 2 26. 12. 06

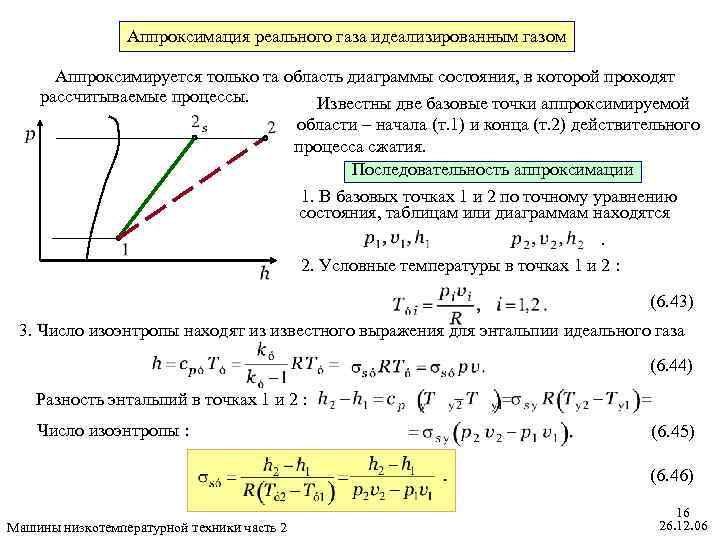Аппроксимация реального газа идеализированным газом Аппроксимируется только та область диаграммы состояния, в которой проходят рассчитываемые процессы. Известны две базовые точки аппроксимируемой области – начала (т. 1) и конца (т. 2) действительного процесса сжатия. Последовательность аппроксимации 1. В базовых точках 1 и 2 по точному уравнению состояния, таблицам или диаграммам находятся. 2. Условные температуры в точках 1 и 2 : (6. 43) 3. Число изоэнтропы находят из известного выражения для энтальпии идеального газа (6. 44) Разность энтальпий в точках 1 и 2 : Число изоэнтропы : (6. 45) (6. 46) Машины низкотемпературной техники часть 2 16 26. 12. 06

Показатель изоэнтропы (6. 47) При расчётах процессов близких к изоэнтропному можно применять зависимость (6. 48) Уравнение процесса Политропный процесс – процесс с постоянной теплоёмкостью (6. 49) Так как то после интегрирования найдём Отсюда теплоёмкость политропного процесса (6. 50) (6. 51) Машины низкотемпературной техники часть 2 17 26. 12. 06

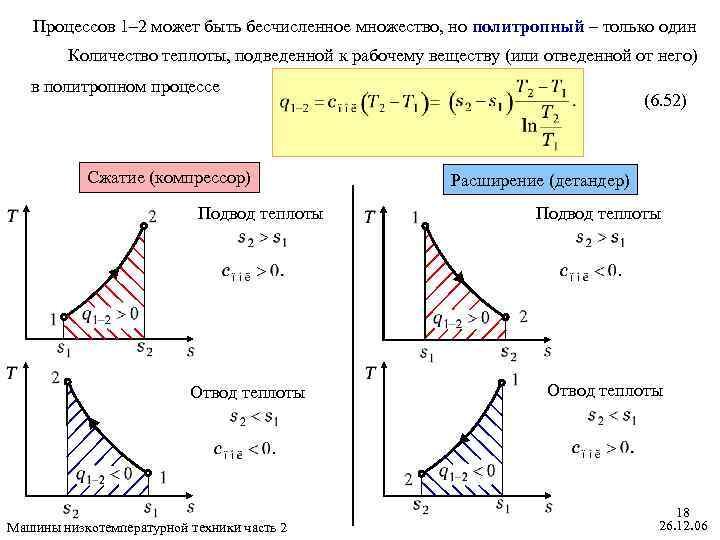Процессов 1– 2 может быть бесчисленное множество, но политропный – только один Количество теплоты, подведенной к рабочему веществу (или отведенной от него) в политропном процессе Сжатие (компрессор) Подвод теплоты Отвод теплоты Машины низкотемпературной техники часть 2 (6. 52) Расширение (детандер) Подвод теплоты Отвод теплоты 18 26. 12. 06

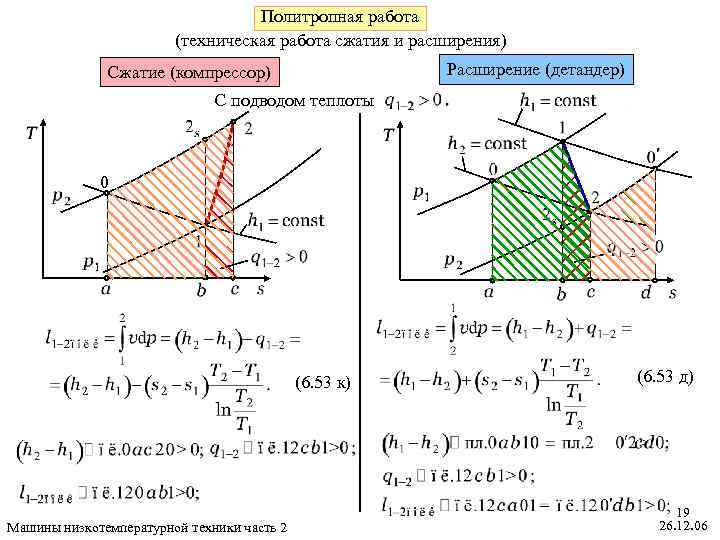Политропная работа (техническая работа сжатия и расширения) Расширение (детандер) Сжатие (компрессор) С подводом теплоты 0 (6. 53 к) Машины низкотемпературной техники часть 2 (6. 53 д) 19 26. 12. 06

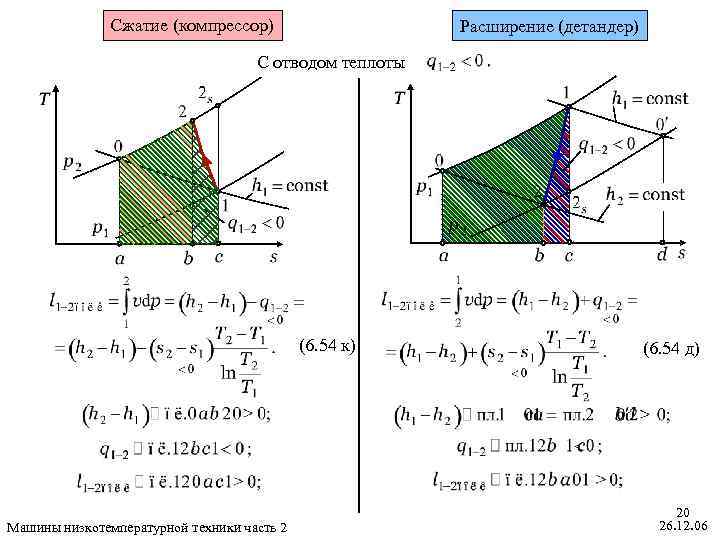Сжатие (компрессор) Расширение (детандер) С отводом теплоты (6. 54 к) Машины низкотемпературной техники часть 2 (6. 54 д) 20 26. 12. 06

Параметры торможения Сумма энтальпии движущегося потока и его кинетической энергии называется энтальпией торможения или полной энтальпией : (6. 55) здесь – статическая энтальпия, вычисленная по статическим давлению и и температуре, измеренными приборами, движущимися вместе с потоком. – скорость потока. Основные методы расчёта в прикладной газовой динамике разработаны применительно к воздуху или продуктам сгорания авиационного топлива, подчиняющихся при умеренных давлениях уравнению состояния идеального газа (1. 28) Энтальпия идеального газа (6. 56) Особенность энтальпии, определяемой таким образом, состоит в том, что при T=0 она равна нулю и значит равна нулю и постоянная энтальпии. Из этого следует, что значение энтальпии, определяемой по формуле (1. 47), можно рассматривать как разность энтальпий между в начале отсчёта при T = 0 и её значением при некоторой температуре T. Машины низкотемпературной техники часть 2 21 26. 12. 06

Отмеченная особенность позволяет определить температуру газа по формуле (6. 57) В расчётных зависимостях прикладной газодинамики идеального газа используют не энтальпию а температуру, поэтому на основании зависимости (1. 48) температуру торможения находят по формуле (6. 58) При прямолинейном движении газа в трубе со скоростью статическое давление может быть измерено непосредственно на стенке канала приёмником А, а давление торможения – с помощью специального приёмника B, входное отверстие которого направлено против движения потока. Температура, измеряемая термометром C, близка к к температуре торможения, так как газ замедляется в пограничном слое до полного торможения у поверхности. Однако, вследствие излучения и теплопроводности газа, часть теплоты теряется и измеренная температура оказывается ниже её точного значения. Машины низкотемпературной техники часть 2 22 08. 12. 06

Измеренная температура (6. 59) Коэффициент восстановления температуры торможения тем меньше, чем выше скорость потока. При дозвуковых скоростях (6. 60) При сверхзвуковых скоростях При малых дозвуковых скоростях можно пользоваться. Для неэкранированных приёмников обычно зависимостью Если применить параметры торможения, то уравнения энергии (6. 32) и (6. 34) можно преобразовать так : Сжатие (компрессор) (6. 32 к), (6. 34 к) Расширение (детандер) (6. 32 д), (6. 34 д) Таким образом внешняя удельная работа, подводимая к компрессору, или отводимая от детандера, если они не обмениваются теплотой с внешними источниками, т. е. являются адиабатными машинами, всегда равна разности энтальпий торможения при входе и выходе машины. 23 Машины низкотемпературной техники часть 2 09. 12. 06

Энтальпия торможения в относительном движении (6. 61) здесь – скорость потока в относительном движении. Знаком «тильда» – змейка, расположенным над символом, будут в дальнейшем обозначаться параметры в относительном движении. Ранее были получены уравнения : (6. 32 к) (6. 32 д) (6. 16 к) (6. 16 д) Приравняв их, сократив разности кинетических энергий и сгруппировав параметры с: одинаковыми индексами найдём : (6. 62 д) (6. 62 к) Постоянная Бернулли в относительном движении (ротальпия). всегда одинакова в любой точке вращающегося колеса. (6. 63) С учётом (6. 61) для обоих случаев компрессора и детандера из (6. 62) найдём : или (6. 64) Значит энтальпия торможения в относительном движении при движении по поверхности цилиндра постоянного радиуса всегда одна и та же и изменяется только при переходе с одного радиуса на другой. 24 Машины низкотемпературной техники часть 2 26. 12. 06

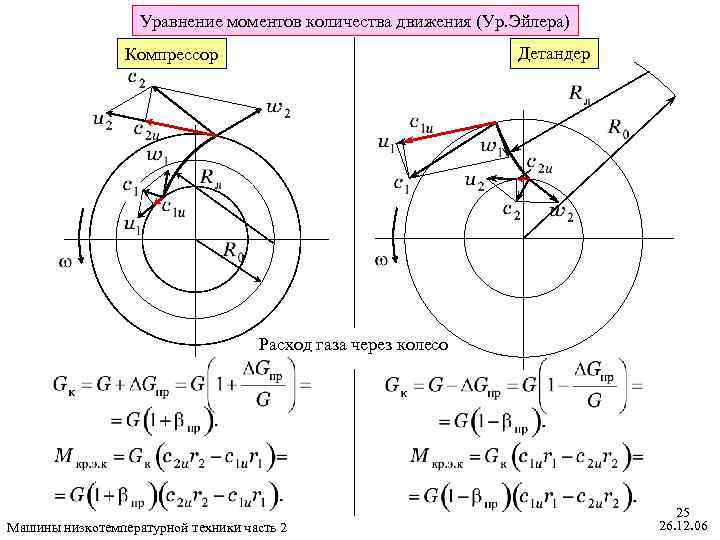Уравнение моментов количества движения (Ур. Эйлера) Детандер Компрессор Расход газа через колесо Машины низкотемпературной техники часть 2 25 26. 12. 06

Компрессор Детандер (6. 65 д) (6. 65 к) При тогда (6. 66 к) (6. 67 к) Частный случай (6. 68 к) Машины низкотемпературной техники часть 2 (6. 68 к) 26 26. 12. 06

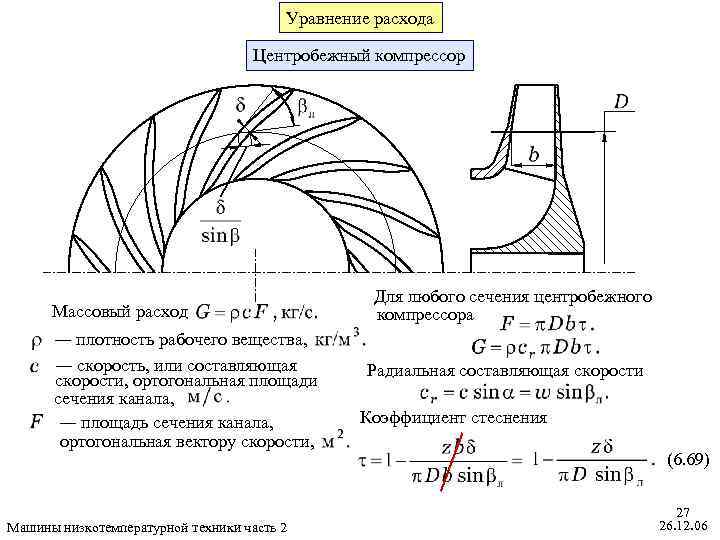Уравнение расхода Центробежный компрессор Массовый расход ― плотность рабочего вещества, ― скорость, или составляющая скорости, ортогональная площади сечения канала, ― площадь сечения канала, ортогональная вектору скорости, Машины низкотемпературной техники часть 2 Для любого сечения центробежного компрессора Радиальная составляющая скорости Коэффициент стеснения (6. 69) 27 26. 12. 06

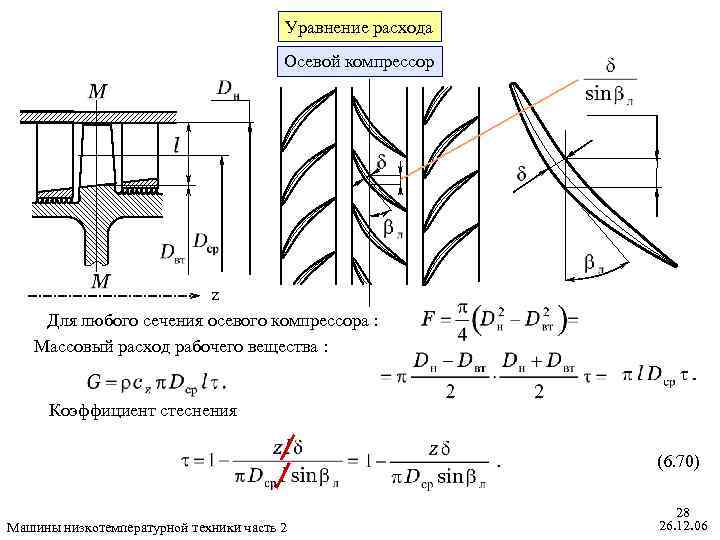Уравнение расхода Осевой компрессор z Для любого сечения осевого компрессора : Массовый расход рабочего вещества : Коэффициент стеснения (6. 70) Машины низкотемпературной техники часть 2 28 26. 12. 06

Компрессор Понятие о к. п. д. Первый подход к определению к. п. д. Детандер Вытекает непосредственно из уравнения импульсов Бернулли и позволяет оценить значение потерянной мощности, затраченной на преодоление сопротивлений. (6. 71 к) Полезная часть внутренней работы компрессора. (6. 71 д) Располагаемая работа детандера Внутренний к. п. д. (6. 72 к) Машины низкотемпературной техники часть 2 (6. 72 д) 29 26. 12. 06

Компрессор Детандер При (6. 73 к) (6. 73 д) При аппроксимации действительного процесса политропным Произвольный реальный газ Считаем (6. 74 к) Машины низкотемпературной техники часть 2 (6. 74 д) 30 26. 12. 06

Компрессор Идеальный или идеализированный газ Обозначим число изоэнтропы (6. 75 к) Машины низкотемпературной техники часть 2 Детандер и политропы (6. 75 к) 31 26. 12. 06

Второй подход к определению к. п. д. состоит в том, что к. п. д. определяют как отношение мощности или работы теоретической машины, в которой осуществляется некоторый эталонный процесс, к мощности или работе действительной машины (для компрессора) или, наоборот, мощности или работы действительной машины к мощности или работе теоретической машины, осуществляющей эталонный процесс ( для детандера). Компрессор Эталонные процессы : Детандер для адиабатных машин – изоэнтропный. для охлаждаемых компрессоров – – изотермный. Произвольный реальный газ (6. 76 к) Машины низкотемпературной техники часть 2 (6. 76 д) 32 26. 12. 06

Идеальный и идеализированный газ Компрессор Детандер (6. 77 к) Машины низкотемпературной техники часть 2 (6. 77 д) 33 26. 12. 06

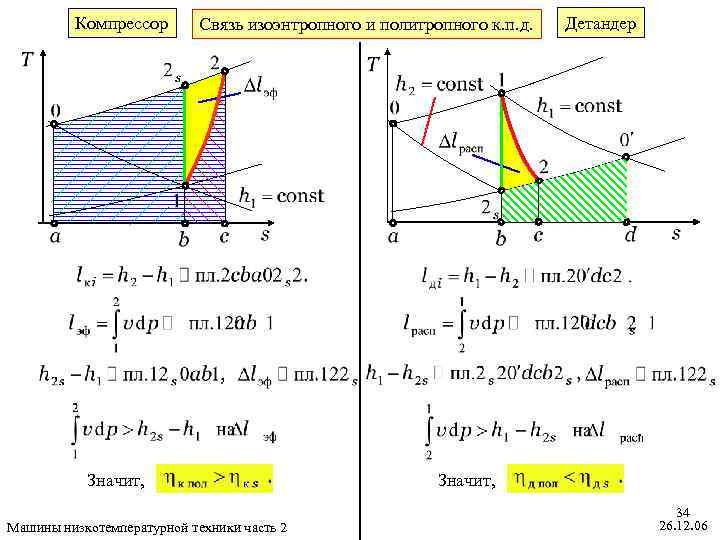Компрессор Связь изоэнтропного и политропного к. п. д. Значит, Машины низкотемпературной техники часть 2 Детандер Значит, 34 26. 12. 06

Связь изоэнтропного и политропного к. п. д. Детандер Компрессор Знаменатели в формулах обоих к. п. д. равны значит, Числители в формулах обоих к. п. д. равны значит, (6. 78 к) (6. 78 д) Идеальный и идеализированный газ (6. 79 к) Машины низкотемпературной техники часть 2 (6. 79 д) 35 26. 12. 06

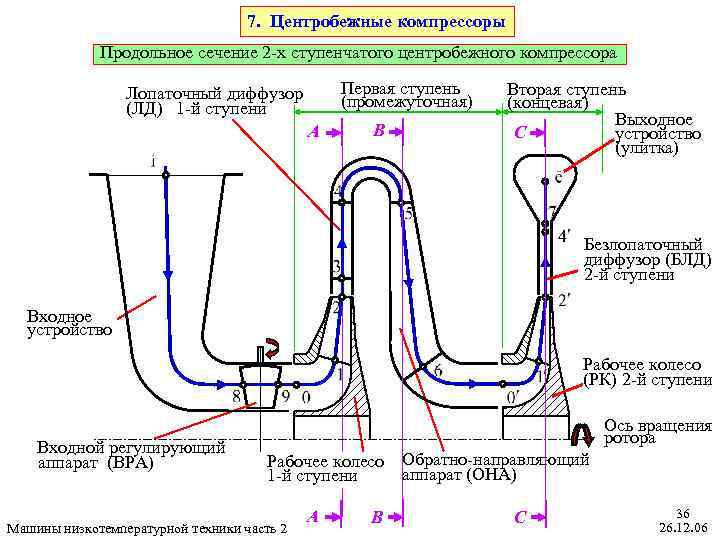7. Центробежные компрессоры Продольное сечение 2 -х ступенчатого центробежного компрессора Первая ступень (промежуточная) Лопаточный диффузор (ЛД) 1 -й ступени A B Вторая ступень (концевая) Выходное C устройство (улитка) Безлопаточный диффузор (БЛД) 2 -й ступени Входное устройство Рабочее колесо (РК) 2 -й ступени Входной регулирующий аппарат (ВРА) Ось вращения ротора Рабочее колесо Обратно-направляющий аппарат (ОНА) 1 -й ступени Машины низкотемпературной техники часть 2 A B C 36 26. 12. 06

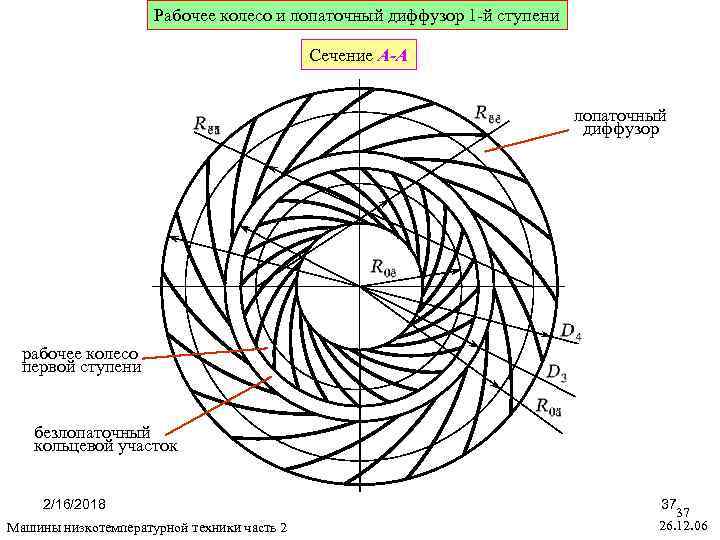Рабочее колесо и лопаточный диффузор 1 -й ступени Сечение А-А лопаточный диффузор рабочее колесо первой ступени безлопаточный кольцевой участок 2/16/2018 Машины низкотемпературной техники часть 2 37 37 26. 12. 06

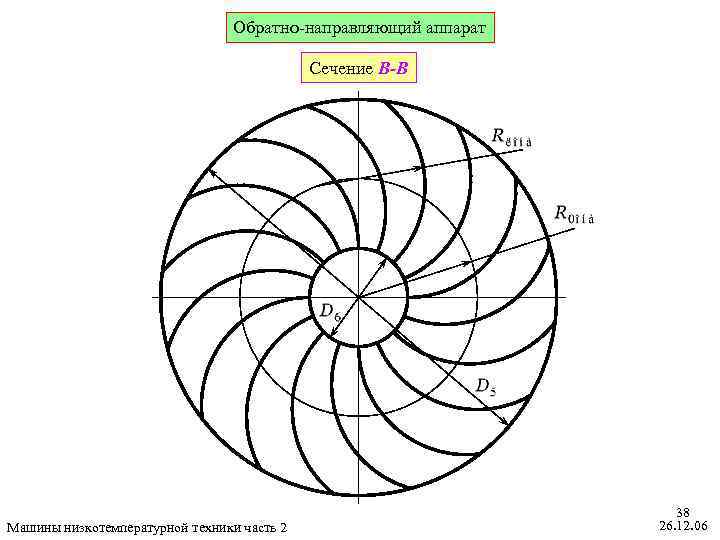Обратно-направляющий аппарат Сечение B-B Машины низкотемпературной техники часть 2 38 26. 12. 06

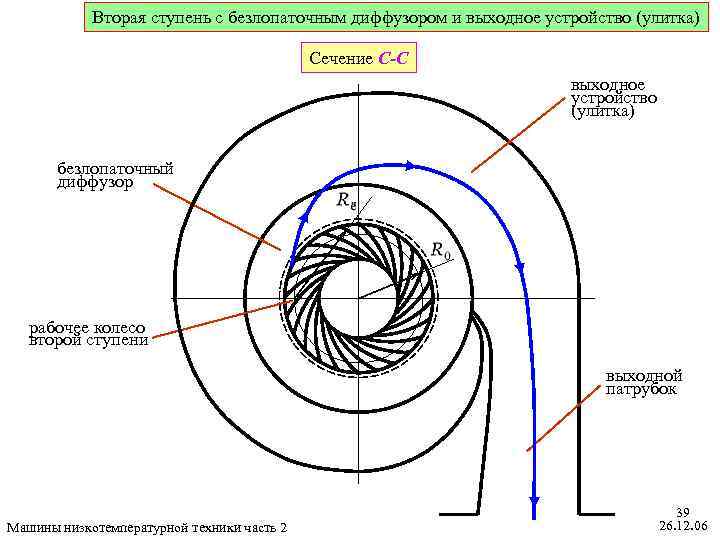Вторая ступень с безлопаточным диффузором и выходное устройство (улитка) Сечение C-C выходное устройство (улитка) безлопаточный диффузор рабочее колесо второй ступени выходной патрубок Машины низкотемпературной техники часть 2 39 26. 12. 06

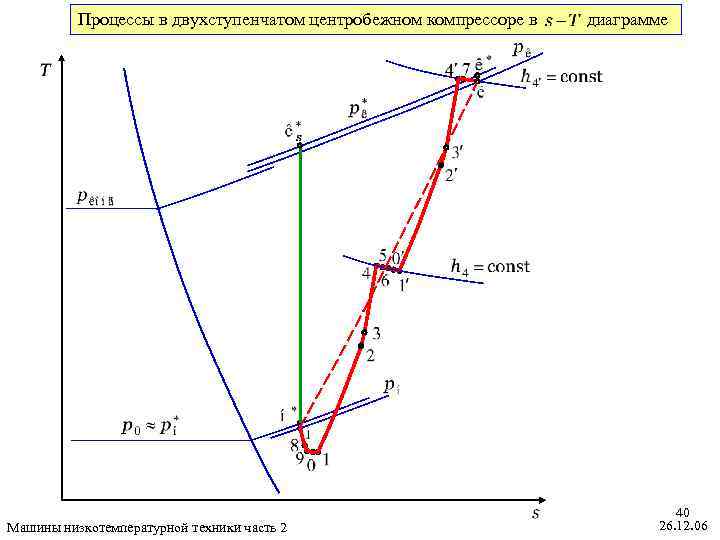Процессы в двухступенчатом центробежном компрессоре в Машины низкотемпературной техники часть 2 диаграмме 40 26. 12. 06

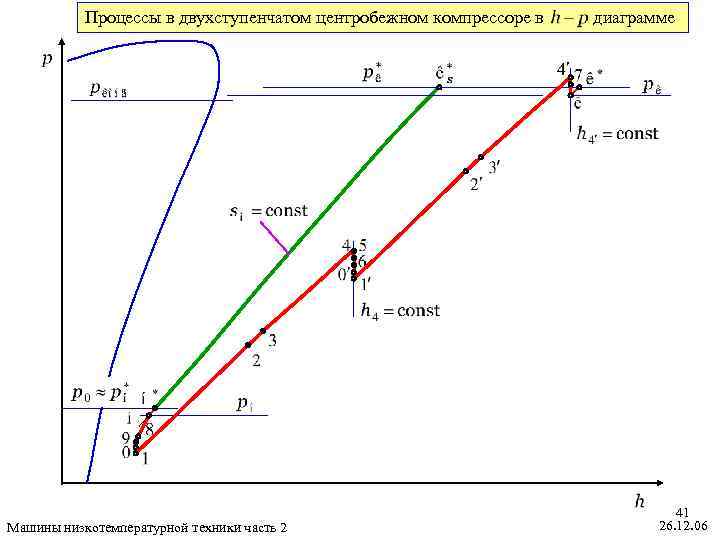Процессы в двухступенчатом центробежном компрессоре в Машины низкотемпературной техники часть 2 диаграмме 41 26. 12. 06

Безразмерные параметры центробежного компрессора Безразмерные параметры – это фактические геометрические размеры или скорости отнесённые к некоторым характерным параметрам, имеющим ту же размерность. Геометрические параметры Характерный размер – наружный диаметр колеса Диаметры Линейные размеры . (7. 1) (7. 2) Скорости Характерная скорость – окружная скорость на наружном диаметре колеса (7. 3) Здесь – частота вращения ротора компрессора, 1/с. Абсолютные скорости (7. 4) Относительные скорости (7. 5) Например : Машины низкотемпературной техники часть 2 и т. п. 42 26. 12. 06 .

Подобие потоков в центробежном компрессоре Газодинамически подобными являются потоки с одинаковыми числами Маха. Кинематически подобными являются потоки, у которых треугольники скоростей подобны. входные кромки Оценка параметров подобия необходима потому, лопаток что компрессоры могут работать при различных давлениях и температурах при всасывании, а также на различных рабочих веществах. Газодинамическое подобие Уравнение расхода в сечении 0 -0 (7. 6) Число Маха в сечении 0 -0 Подставляя это в (7. 6), находим При работе на иных рабочих веществах и при других условиях всасывания На подобных режимах Машины низкотемпературной техники часть 2 43 26. 12. 06

Отсюда условие подобия значит, (7. 7) Если нужно привести расход к стандартным начальным условиям, то (7. 8) здесь – фактический расход при условиях на всасывании – расход, приведенный к стандартным условиям на всасывании . Кинематическое подобие Чтобы обеспечить подобие треугольников скоростей необходимо, чтобы было соблюдено равенство или Перевернув последнее соотношение, что не изменяет равенства, получим При равенстве Но будет или (7. 9) связаны соотношением Подставив это выражение в (7. 8), найдём новое число подобия или Машины низкотемпературной техники часть 2 (7. 10) 44 26. 12. 06

Так как скорости потока во входном устройстве или при входе в колесо невелики, то можно допустить Тогда необходимые условия газодинамического (7. 11) и кинематического подобия примут такой вид (7. 12) В случае, идеального газа с постоянным показателем изоэнтропы и скоростью звука, зависящей только от температуры, режимы работы с одинаковыми числами подобия (7. 7, 7. 9) или (7. 11 и 7. 12) обеспечивает кинематическое подобие потока и при выходе колеса независимо от значений начального давления и температуры. При сжатии одного и того же реального газа при различных начальных условиях будет обеспечиваться приближённое подобие потока при выходе колеса, если значения показателя изоэнтропы и коэффициента сжимаемости газа не будут сильно отличаться. При сжатии разных реальных газов газодинамическое подобие при входе в колесо не гарантирует подобия потоков при выходе колеса. Особенно сильное различие в числах Маха и кинематике потока при выходе колеса будет наблюдаться при сжатии высокомолекулярных и низкомолекулярных газов, с сильно отличающимися значениями показателей изоэнтропы и коэффициента сжимаемости. Машины низкотемпературной техники часть 2 45 26. 12. 06

Для идеального или идеализированного газа Скорость звука в заторможенном потоке при входе в компрессор Условие подобия (7. 11) (7. 13) Чтобы обеспечить подобие при работе на газе ( ) (7. 14) нужно выдерживать окружную скорость При работе на одном и том же газе из (7. 13) и Число подобия (7. 12) представим так Машины низкотемпературной техники часть 2 (7. 15) (7. 16) 46 26. 12. 06

Тогда условие подобия (7. 12) Для обеспечения подобия при работе на газе ( ) нужен расход (7. 17) (7. 18) При работе на одном и том же газе (7. 19) Машины низкотемпературной техники часть 2 47 26. 12. 06

На практике применяются такие числа подобия Условное число Маха по окружной скорости на наружном диаметре колеса (7. 20) Условное число Маха по скорости во входном сечении колеса (7. 21) Условное число Маха по скорости во входном сечении компрессора (7. 22) Два режима работы компрессора динамического действия подобны, если для них одинаковы пары чисел подобия и или и Значит, одновременно должны выдерживаться равенства. или Машины низкотемпературной техники часть 2 (7. 23) 48 26. 12. 06

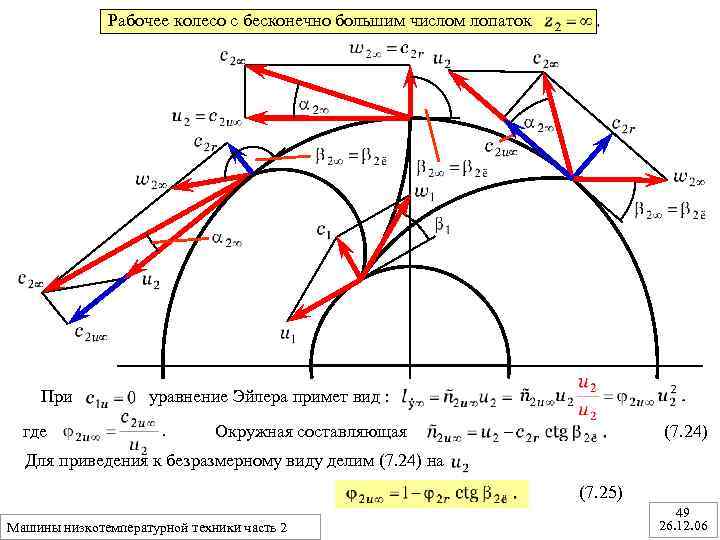Рабочее колесо с бесконечно большим числом лопаток При где уравнение Эйлера примет вид : (7. 24) Окружная составляющая Для приведения к безразмерному виду делим (7. 24) на (7. 25) Машины низкотемпературной техники часть 2 49 26. 12. 06

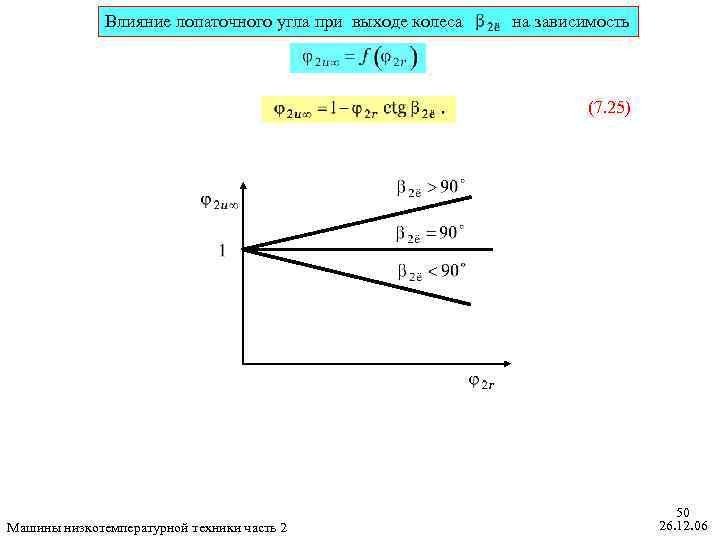Влияние лопаточного угла при выходе колеса на зависимость (7. 25) Машины низкотемпературной техники часть 2 50 26. 12. 06

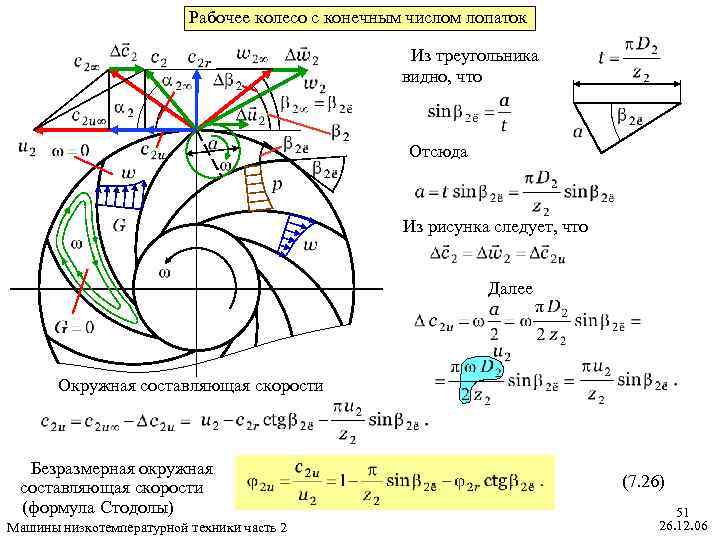Рабочее колесо с конечным числом лопаток Из треугольника видно, что Отсюда Из рисунка следует, что Далее Окружная составляющая скорости Безразмерная окружная составляющая скорости (формула Стодолы) Машины низкотемпературной техники часть 2 (7. 26) 51 26. 12. 06

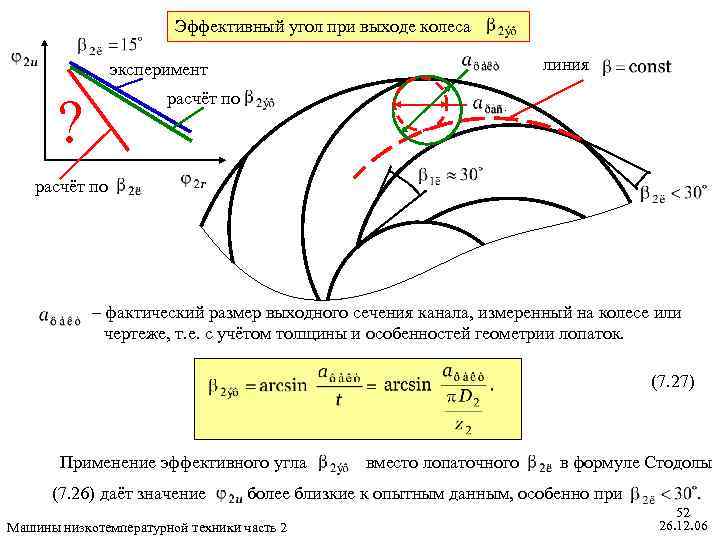Эффективный угол при выходе колеса линия эксперимент расчёт по ? расчёт по – фактический размер выходного сечения канала, измеренный на колесе или чертеже, т. е. с учётом толщины и особенностей геометрии лопаток. (7. 27) Применение эффективного угла (7. 26) даёт значение вместо лопаточного в формуле Стодолы более близкие к опытным данным, особенно при Машины низкотемпературной техники часть 2 52 26. 12. 06

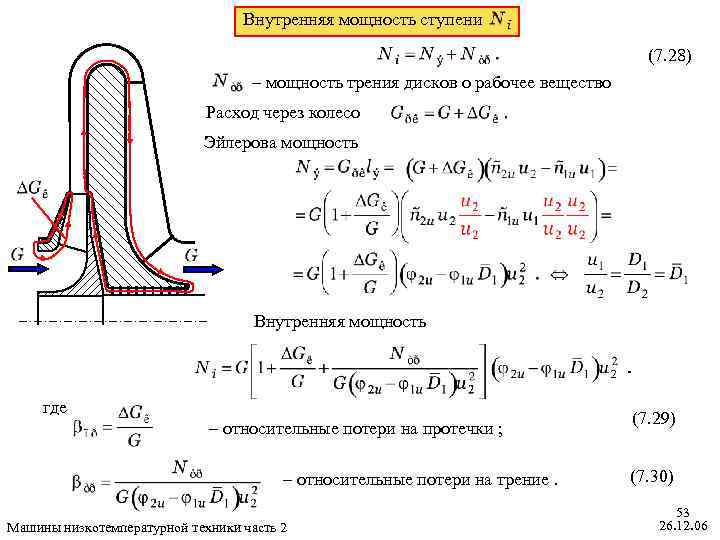Внутренняя мощность ступени (7. 28) – мощность трения дисков о рабочее вещество Расход через колесо Эйлерова мощность Внутренняя мощность где – относительные потери на протечки ; – относительные потери на трение. Машины низкотемпературной техники часть 2 (7. 29) (7. 30) 53 26. 12. 06

Окончательно (7. 31) Коэффициент мощности (7. 32) При отсутствии закрутки потока при входе колеса (7. 33) Внутренняя удельная работа ступени (7. 34) или где Эйлерова работа (7. 35) Машины низкотемпературной техники часть 2 54 26. 12. 06

Из первого закона термодинамики было получено (6. 71) Отсюда обычно определяют . (7. 36) При примерном равенстве скоростей при входе и выходе машины (7. 37) Эффективная работа ступени в случае, когда внутренний к. п. д. определяется как политропный. (7. 38) Коэффициент эффективной работы (7. 39) Отсюда коэффициент мощности (7. 40) Внутренний (политропный) к. п. д. учитывает все потери в ступени, включая потери на протечки и трение дисков. Машины низкотемпературной техники часть 2 55 26. 12. 06

Гидравлический к. п. д. (7. 41) Гидравлический к. п. д. учитывает только потери, связанные с движением рабочего вещества в проточной части. Коэффициент реактивности ступени центробежного компрессора – это отношение теплоперепада, срабатываемого в колесе, к теплоперепаду всей ступени (7. 42) Внутренняя работа ступени (7. 43) Отсюда теплоперепад в колесе (7. 44) Машины низкотемпературной техники часть 2 56 26. 12. 06

Подставив (7. 44) в (7. 42), найдём Разделив числитель дроби на , находящийся в знаменателе, окончательно найдём (7. 45) Для практических расчётов при проектировании компрессоров удобнее использовать коэффициент реактивности, у которого в числителе находится теплоперепад от состояния торможения при входе, т. е. без учёта кинетической энергии при входе колеса (7. 46) Машины низкотемпературной техники часть 2 57 26. 12. 06

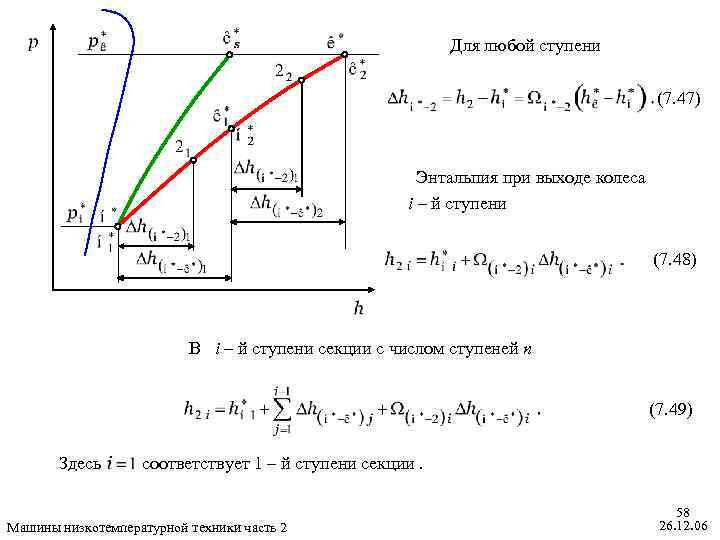Для любой ступени (7. 47) Энтальпия при выходе колеса i – й ступени (7. 48) В i – й ступени секции с числом ступеней n (7. 49) Здесь соответствует 1 – й ступени секции. Машины низкотемпературной техники часть 2 58 26. 12. 06

Для идеального (идеализированного) газа Температура торможения при входе i – ю ступень компрессора или секции (7. 50) Числа изоэнтропы и политропы Статическая температура при выходе колеса i – ступени Плотность при выходе колеса i – й ступени Коэффициент увеличения плотности Машины низкотемпературной техники часть 2 (7. 51) (7. 52) (7. 53) 59 26. 12. 06

Определение размеров рабочего колеса Уравнение расхода при входе и выходе колеса : (7. 54) Переходим к безразмерным параметрам : (7. 55) или (7. 56) Коэффициенты стеснения (7. 57) (7. 58) Здесь безразмерная толщина лопатки Коэффициент 0, 5 учитывает заострение лопатки Машины низкотемпературной техники часть 2 (7. 59) 60 26. 12. 06

Определение размеров радиального рабочего колеса, когда известна окружная скорость. Определив (7. 53) как показано выше, из уравнения расхода (7. 56) находим : (7. 60) находят либо по графику 9. 7 учебника, либо находят Коэффициент расхода по формуле (7. 61) Здесь – угол выхода потока из колеса, обычно соответствующий наибольшей эффективности колеса и ступени в целом. Для первой ступени Так как у всех ступеней в компрессоре или секции наружные диаметры всех колёс делают одинаковыми , то для второй и последующих ступеней из того-же уравнения расхода находят : (7. 62) Машины низкотемпературной техники часть 2 61 26. 12. 06

Безразмерная высота лопатки при выходе колеса может изменяться в пределах Уменьшение её ниже 0, 02 приводит к снижению к. п. д. ступени. Наружный диаметр колеса должен быть ступени. Определение диаметров и , чтобы не снизить к. п. д. . Увеличение свыше 0, 30 приводит к снижению к. п. д. Значение диаметра зависит от диаметра вала, на котором расположено колесо. По опыту Невского завода средний диаметр вала приближённо находят исходя из критической частоты вращения по формуле : (7. 63) Здесь – среднее арифметическое из трёх наибольших диаметров вала, м. – среднее арифметическое наружных диаметров колёс всех ступеней, м. – число ступеней. Первая критическая частота вращения должна быть выше рабочей на 20÷ 30%. (7. 64) Машины низкотемпературной техники часть 2 62 26. 12. 06

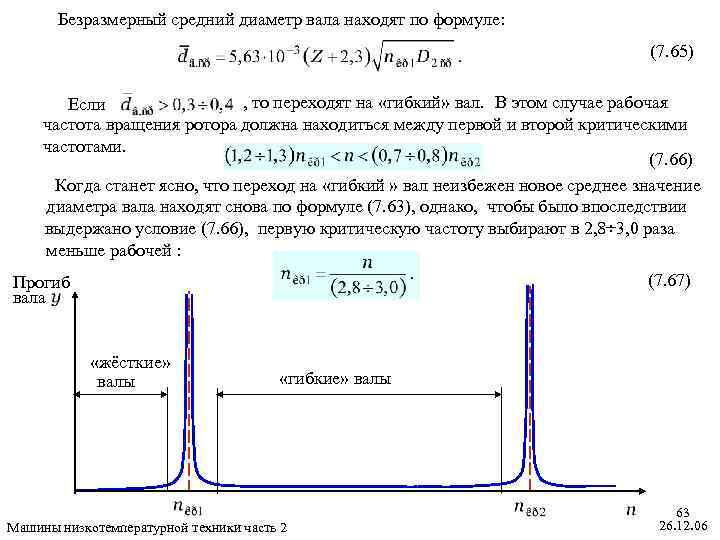Безразмерный средний диаметр вала находят по формуле: (7. 65) , то переходят на «гибкий» вал. В этом случае рабочая Если частота вращения ротора должна находиться между первой и второй критическими частотами. (7. 66) Когда станет ясно, что переход на «гибкий » вал неизбежен новое среднее значение диаметра вала находят снова по формуле (7. 63), однако, чтобы было впоследствии выдержано условие (7. 66), первую критическую частоту выбирают в 2, 8÷ 3, 0 раза меньше рабочей : (7. 67) Прогиб вала «жёсткие» валы «гибкие» валы Машины низкотемпературной техники часть 2 63 26. 12. 06

определяется из условия минимума относительной скорости при входе на лопатки по формуле : (7. 68) Здесь – коэффициент ускорения потока на участке осерадиального поворота потока 0 -1. – коэффициент увеличения диаметра. Оптимальные значения по опытам В. Е. Евдокимова находятся в пределах : (7. 69) Высота лопатки при входе в колесо : (7. 70) Машины низкотемпературной техники часть 2 64 26. 12. 06

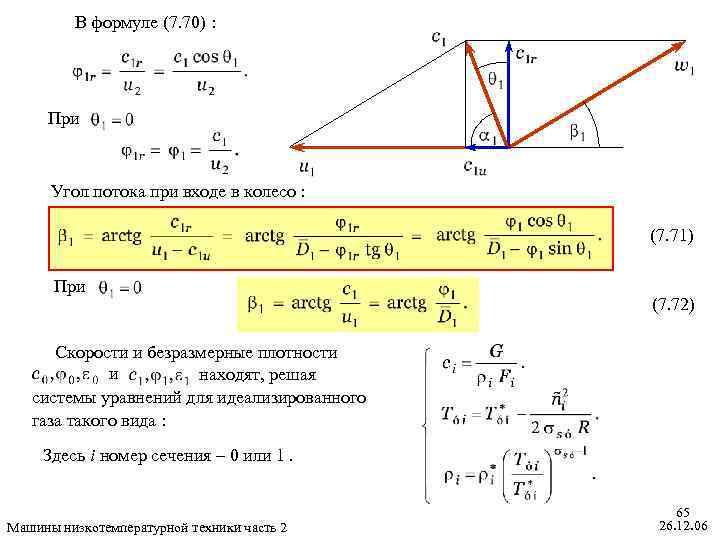В формуле (7. 70) : При Угол потока при входе в колесо : (7. 71) При (7. 72) Скорости и безразмерные плотности и находят, решая системы уравнений для идеализированного газа такого вида : Здесь i номер сечения – 0 или 1. Машины низкотемпературной техники часть 2 65 26. 12. 06

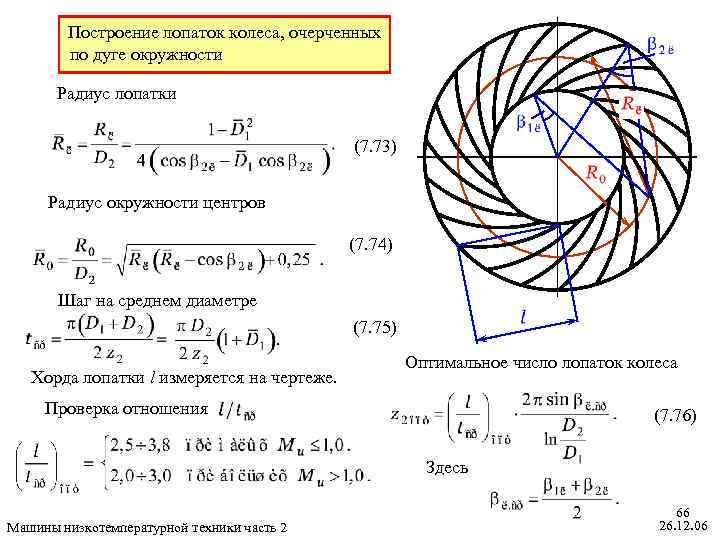Построение лопаток колеса, очерченных по дуге окружности Радиус лопатки (7. 73) Радиус окружности центров (7. 74) Шаг на среднем диаметре (7. 75) Хорда лопатки l измеряется на чертеже. Оптимальное число лопаток колеса Проверка отношения (7. 76) Здесь Машины низкотемпературной техники часть 2 66 26. 12. 06

Определение размеров радиального рабочего колеса, когда известна частота вращения. Из уравнения расхода (7. 56) с учётом того, что находим : (7. 77) Отсюда (7. 78) – заранее неизвестна, поэтому вначале задаётся, а затем проверяется. Далее расчёт проводится в такой последовательности : Окружная скорость (7. 79) Удельная работа ступеней (здесь считается, что все колёса одинаковы, т. е. одинаковы ) (7. 80) Число ступеней (округляется) (7. 81) Уточнение окружной скорости (7. 82) Машины низкотемпературной техники часть 2 67 26. 12. 06

Далее находится и уточняется колеса 1 – й ступени, для чего в уравнение расхода (7. 77) подставляется новое, уточнённое значение (7. 83) При необходимости получить требуемое значение – возврат к (7. 78) и итерация. После этого расчёт проводится так же, как и при известной Диффузоры холодильных центробежных компрессоров кинетическая энергия при выходе У ступеней с колёсами колеса составляет от 25 до 45% от внутренней работы ступени. Кинетическая энергия преобразуется в энергию давления в диффузоре, скорость потока в котором уменьшается за счёт увеличения площади сечения. Увеличение эффективной работы диффузора сдерживается сопроти- влением на преодоления которого затрачивается часть срабатываемого в диффузоре телоперепада. Машины низкотемпературной техники часть 2 68 26. 12. 06

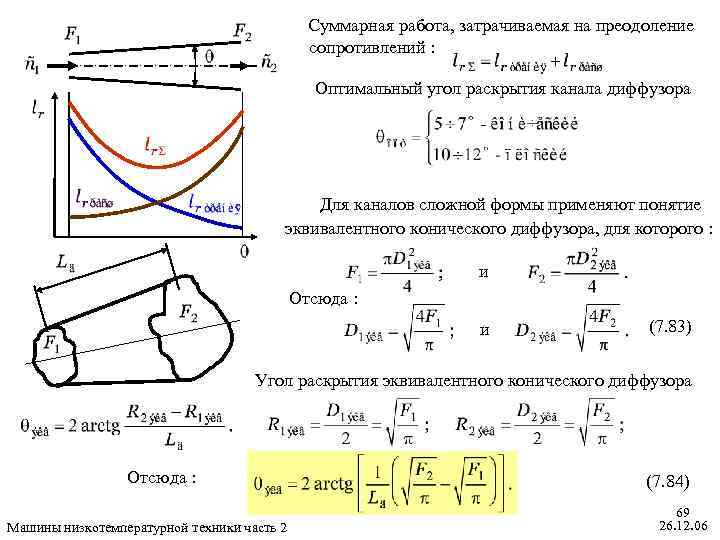Суммарная работа, затрачиваемая на преодоление сопротивлений : Оптимальный угол раскрытия канала диффузора Для каналов сложной формы применяют понятие эквивалентного конического диффузора, для которого : и Отсюда : и (7. 83) Угол раскрытия эквивалентного конического диффузора Отсюда : Машины низкотемпературной техники часть 2 (7. 84) 69 26. 12. 06

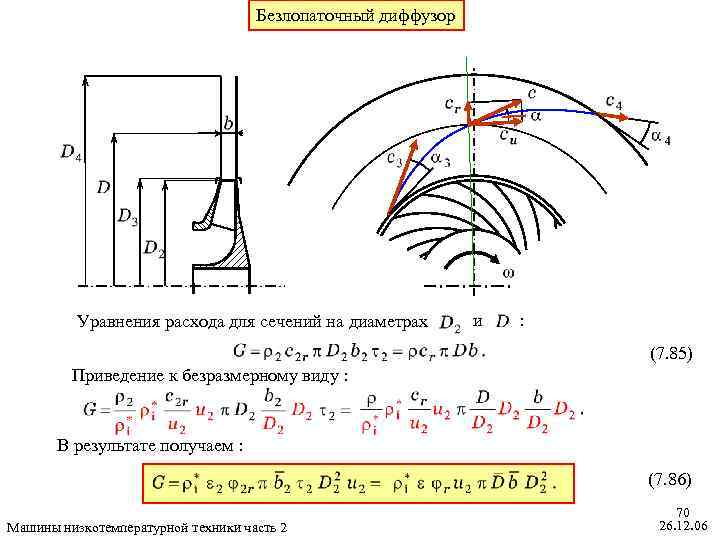Безлопаточный диффузор Уравнения расхода для сечений на диаметрах и : (7. 85) Приведение к безразмерному виду : В результате получаем : (7. 86) Машины низкотемпературной техники часть 2 70 26. 12. 06

Из (7. 86) находим коэффициент расхода на произвольном диаметре : (7. 87) Уравнение сохранения момента количества движения : (7. 88) Здесь – коэффициент, учитывающий потерю момента количества движения из-за трения потока о стенки диффузора. (7. 89) Коэффициент трения находится по данным Никурадзе. Эквивалентный диаметр безлопаточного диффузора Из (7. 88) находим и сразу же приводим к безразмерному виду : (7. 90) Машины низкотемпературной техники часть 2 71 26. 12. 06

Угол потока на произвольном радиусе БЛД (7. 91) Иногда полагают, что трение и сжимаемость компенсируют друга, т. е. считают, что Тогда (7. 92) При Безразмерная скорость на произвольном диаметре из (7. 87) и (7. 90) : (7. 93) Известно, что Тогда из уравнения расхода находим на произвольном диаметре : (7. 94) Машины низкотемпературной техники часть 2 72 26. 12. 06

Для того, чтобы уменьшить потери, поток в ОНА рекомендуют незначительно ускорять. Для этого принимают (7. 95) Коэффициент уменьшения скорости в диффузоре (7. 96) Безразмерный диаметр при выходе диффузора находим из (7. 94) : (7. 97) В противном случае нужно переходить Рекомендованные значения к лопаточному диффузору. Основы расчёта БЛД Реальный газ Энтальпия при выходе БЛД (7. 98) Удельная работа, затраченная на преодоление сопротивлений находится в предположении, что Машины низкотемпературной техники часть 2 (7. 99) 73 26. 12. 06

Температуру при выходе БЛД находят из выражения где теплоёмкость политропного процесса в компрессоре была определена ранее : Плотность при выходе БЛД находится из уравнения состояния, таблиц или диаграммы состояния : Безразмерная плотность при выходе БЛД : (7. 100) (6. 51) (7. 102) Идеальный (идеализированный) газ. Температура при выходе БЛД : (7. 103) Число политропы процесса в компрессоре (7. 104) Безразмерная плотность при выходе БЛД находится в предположении, что параметры при выходе колеса уже определены (7. 105) Машины низкотемпературной техники часть 2 74 26. 12. 06

Зависимость отношения плотностей от безразмерной скорости на произвольном диаметре БЛД может быть получена из следующих соображений : Температура торможения при выходе колеса компрессора : (7. 106) Далее Аналогично для любого сечения после колеса : Отношение плотностей находится из уравнения политропы : (7. 107) Машины низкотемпературной техники часть 2 75 26. 12. 06

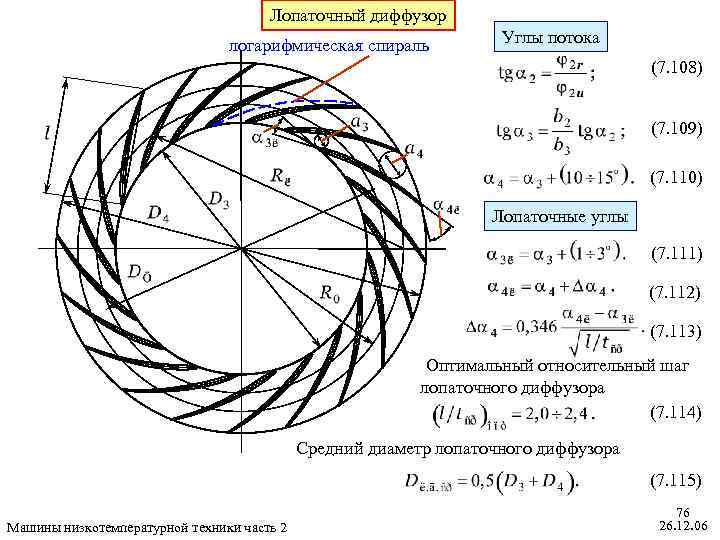Лопаточный диффузор логарифмическая спираль Углы потока (7. 108) (7. 109) (7. 110) Лопаточные углы (7. 111) (7. 112) (7. 113) Оптимальный относительный шаг лопаточного диффузора (7. 114) Средний диаметр лопаточного диффузора (7. 115) Машины низкотемпературной техники часть 2 76 26. 12. 06

Основные размеры Так как число лопаток выбирают по оптимальному значению густоты решётки, сначала неизвестен, то, совместно решая (7. 112) и (7. 113), находим а угол (7. 116) Диаметр расположения входных кромок лопаток диффузора находят из уравнения подобного (7. 97) (7. 117) Здесь Рекомендуется Радиусы лопаток и окружности центров (7. 118) Машины низкотемпературной техники часть 2 (7. 119) 77 26. 12. 06

Пересчёт безразмерных величин в физические размеры ведётся по общим формулам Число лопаток диффузора находится по формуле (7. 120) Толщина лопаток находится в пределах и может сильно повлиять на характеристику. Формально она не влияет ни на , ни на углы , но изменение толщины лопатки вызывает изменение площади входных сечений, определяемой размером. Соответственно изменяется и суммарная площадь входных сечений и коэффициент диффузорности косого среза (7. 121) Оптимальное значение Увеличение приводит к сдвигу характеристик в область более высоких расходов, уменьшение – в область более низких расходов. Машины низкотемпературной техники часть 2 78 26. 12. 06

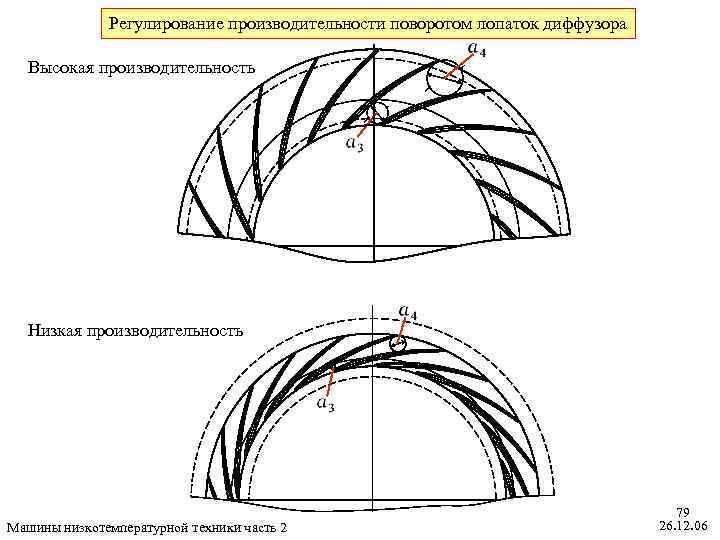Регулирование производительности поворотом лопаток диффузора Высокая производительность Низкая производительность Машины низкотемпературной техники часть 2 79 26. 12. 06

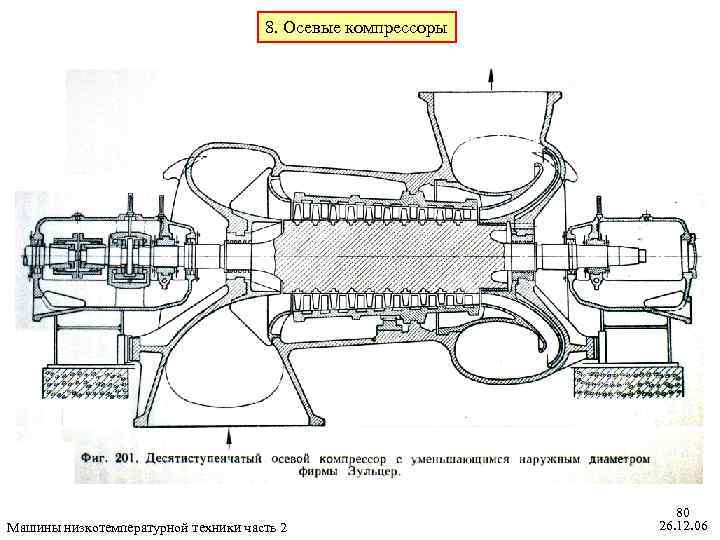8. Осевые компрессоры Машины низкотемпературной техники часть 2 80 26. 12. 06

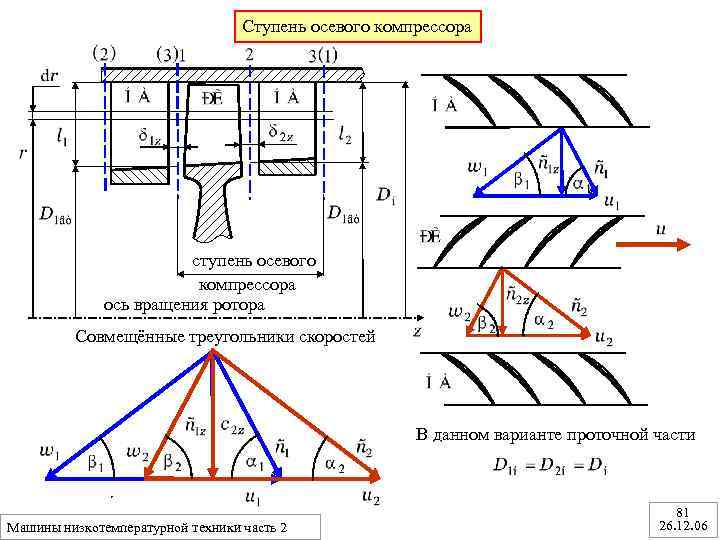Ступень осевого компрессора ступень осевого компрессора ось вращения ротора Совмещённые треугольники скоростей В данном варианте проточной части Машины низкотемпературной техники часть 2 81 26. 12. 06

Основные уравнения для элементарной ступени Уравнение импульсов (Бернулли) Для рабочего колеса (в относительном движении) (8. 1) Для направляющего аппарата (8. 2) Уравнение энергии Для рабочего колеса (в относительном движении) (8. 3) Для направляющего аппарата (8. 4) Уравнение момента количества движения (8. 5) Для ступени в целом (8. 6) (8. 7) Машины низкотемпературной техники часть 2 82 26. 12. 06

или так как Энтальпия торможения в относительном движении но так как , поэтому то (8. 8) Безразмерные параметры осевого компрессора Характерный размер – Характерная скорость – – скорость на радиусе Для элементарной ступени Для ступени – наружный диаметр ступени ; – на наружном диаметре. где (8. 9) (8. 10) Коэффициенты теоретической и изоэнтропной работ Элементарная ступень (8. 11) (8. 12) Ступень в целом (8. 13) (8. 14) Машины низкотемпературной техники часть 2 83 26. 12. 06

Коэффициент реактивности ступени Реальная ступень (8. 15) Для элементарной ступени, когда будет : Окончательно кинематический коэффициент реактивности (8. 16) Этот коэффициент реактивности элементарной ступени полностью определяется треугольниками скоростей, потому и назван «кинематическим» . Машины низкотемпературной техники часть 2 84 26. 12. 06

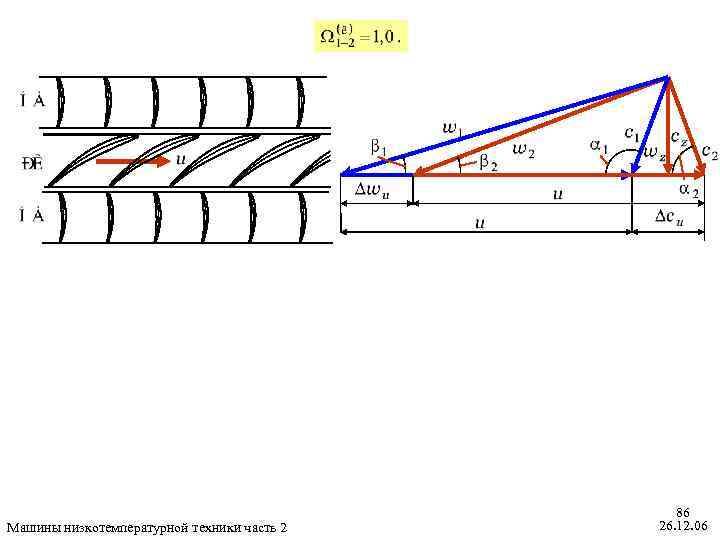
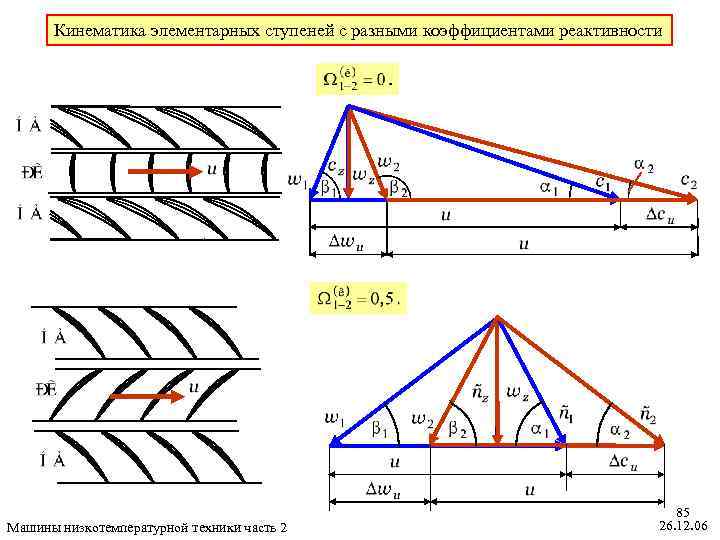Кинематика элементарных ступеней с разными коэффициентами реактивности Машины низкотемпературной техники часть 2 85 26. 12. 06

Машины низкотемпературной техники часть 2 86 26. 12. 06

Машины низкотемпературной техники часть 2 87 26. 12. 06

Машины низкотемпературной техники часть 2 88 26. 12. 06

Машины низкотемпературной техники часть 2 89 26. 12. 06

Машины низкотемпературной техники часть 2 90 26. 12. 06

9. Расширительные машины для холодильной техники и низкопотенциальной энергетики Существует два класса расширительных машин. Расширительные машины объёмного принципа действия – расширение происходит в в замкнутой полости изменяющегося объёма, периодически заполняемой рабочим веществом в процессе впуска и освобождающейся от него в процессе выталкивания или выхлопа. Энергия давления непосредственно преобразуется в механическую. Все процессы идут в строго определённой последовательности : впуск расширение выталкивание (выхлоп) обратное сжатие. Это поршневые, винтовые, спиральные и ротационные детандеры. Машины низкотемпературной техники часть 2 91 26. 12. 06

Расширительные машины динамического принципа действия – расширение происходит непрерывно от точки к точке по проточной части. Энергия давления преобразуется сначала в кинетическую энергию, а затем – в механическую. Преобразование энергии происходит в каналах неподвижных и вращающихся лопаточных решеток, расположенных друг за другом. В неподвижной решётке часть энергии давления преобразуется в кинетическую энергию, которая передаётся вращающемуся колесу, где и преобразуется в механическую энергию. Оставшаяся часть энергии давления преобразуется в колесе практически одновременно в кинетическую и механическую энергию. Это осевые и радиальные расширительные машины (детандеры) Машины низкотемпературной техники часть 2 92 26. 12. 06

Машины низкотемпературной техники часть 2 93 26. 12. 06

Машины низкотемпературной техники часть 2 94 26. 12. 06

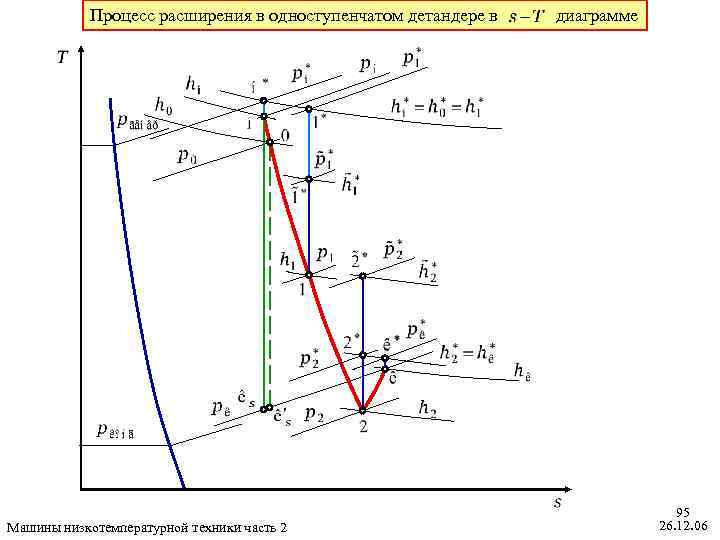Процесс расширения в одноступенчатом детандере в Машины низкотемпературной техники часть 2 диаграмме 95 26. 12. 06

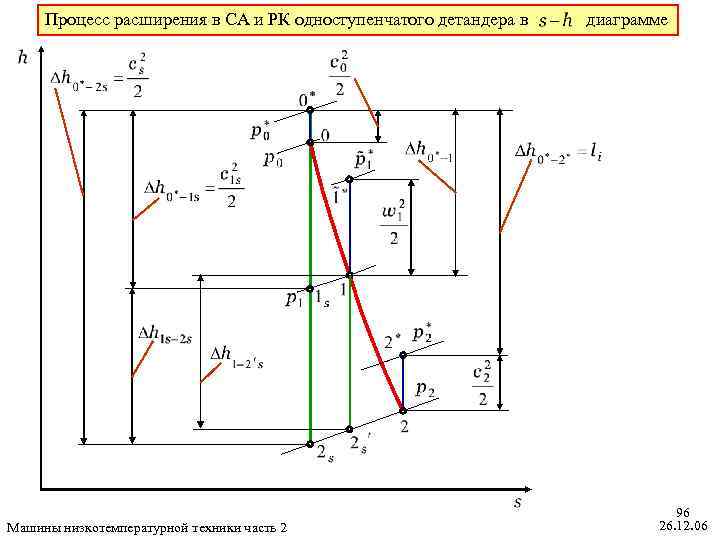Процесс расширения в СА и РК одноступенчатого детандера в Машины низкотемпературной техники часть 2 диаграмме 96 26. 12. 06

Безразмерные параметры расширительных турбомашин Характерный геометрический размер ● для осевых турбомашин – наружный диаметр при входе колеса ; – наружный диаметр колеса. ● для радиальных турбомашин Характерная скорость ● для осевых и диагональных турбомашин (9. 1) Здесь ● для радиальных турбомашин (9. 2) (9. 3) Коэффициент радиальности осевые и диагональные (9. 4) радиально – осевые (9. 5) радиальные (9. 6) Машины низкотемпературной техники часть 2 97 26. 12. 06

Безразмерные кинематические параметры осевые и диагональные (9. 7) (9. 8) радиальные и радиально – осевые (9. 9) (9. 10) Коэффициенты расхода осевые и диагональные радиальные и радиально – осевые Машины низкотемпературной техники часть 2 (9. 11) (9. 12) 98 26. 12. 06

Условные числа Маха По окружной скорости (9. 13) По расходной скорости ● в сечении «н» при входе в машину (9. 14) ● в сечении « 0» при входе в сопловой аппарат (9. 15) При испытаниях одной и той же машины на одном и том же рабочем веществе множитель из рассмотрения исключают и используют только комплекс – параметр расхода, который для идеального газа имеет вид Машины низкотемпературной техники часть 2 99 26. 12. 06

Внутренняя мощность ступени расширительной турбомашины (9. 16) Эйлерова работа (9. 17) Здесь Для осевых и диагональных турбин Коэффициент эйлеровой работы (9. 18) При Значит Эйлерова мощность С учётом протечек в ступени (9. 19) Машины низкотемпературной техники часть 2 100 26. 12. 06

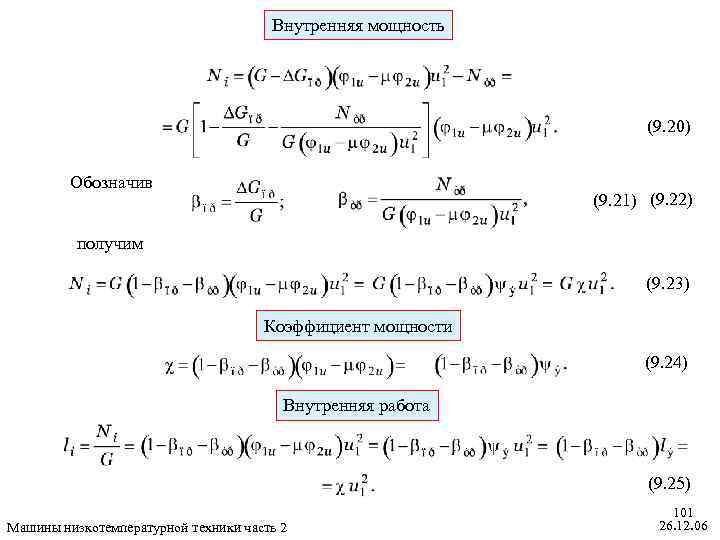Внутренняя мощность (9. 20) Обозначив (9. 21) (9. 22) получим (9. 23) Коэффициент мощности (9. 24) Внутренняя работа (9. 25) Машины низкотемпературной техники часть 2 101 26. 12. 06

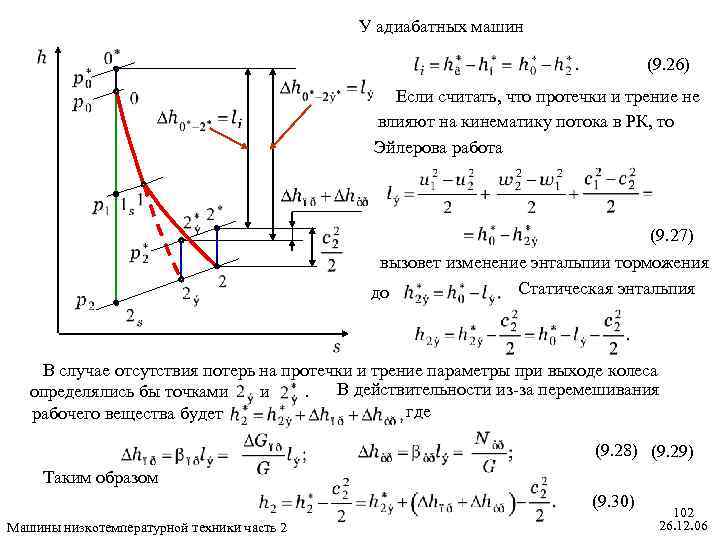У адиабатных машин (9. 26) Если считать, что протечки и трение не влияют на кинематику потока в РК, то Эйлерова работа (9. 27) вызовет изменение энтальпии торможения Статическая энтальпия до В случае отсутствия потерь на протечки и трение параметры при выходе колеса В действительности из-за перемешивания определялись бы точками и. где рабочего вещества будет (9. 28) (9. 29) Таким образом (9. 30) Машины низкотемпературной техники часть 2 102 26. 12. 06

Внутренняя работа (9. 31) При расчётах рекомендуется принимать (9. 32) Машины низкотемпературной техники часть 2 103 26. 12. 06

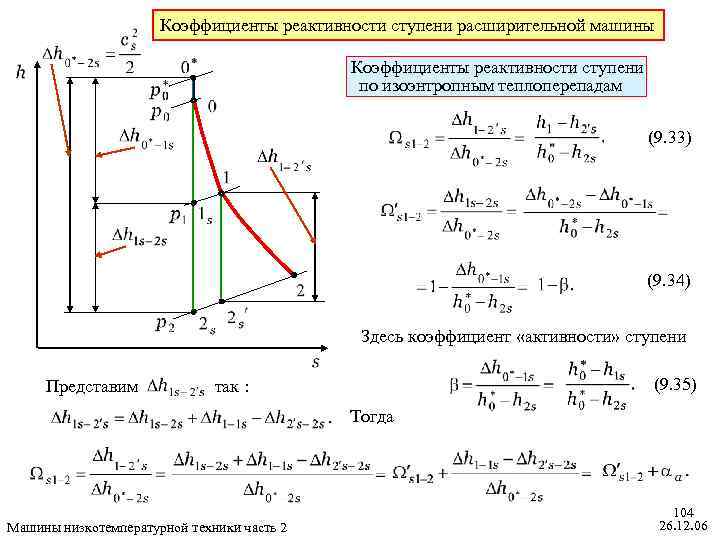Коэффициенты реактивности ступени расширительной машины Коэффициенты реактивности ступени по изоэнтропным теплоперепадам (9. 33) (9. 34) Здесь коэффициент «активности» ступени Представим (9. 35) так : Тогда Машины низкотемпературной техники часть 2 104 26. 12. 06

Окончательно (9. 36) Коэффициент возврата теплоты (9. 37) Обычно при небольших отношениях давления не учитывать. Это значит, можно полагать, что и его можно не (9. 38) Это позволяет упростить определение теплоперепада в сопловом аппарате (9. 39) Машины низкотемпературной техники часть 2 105 26. 12. 06

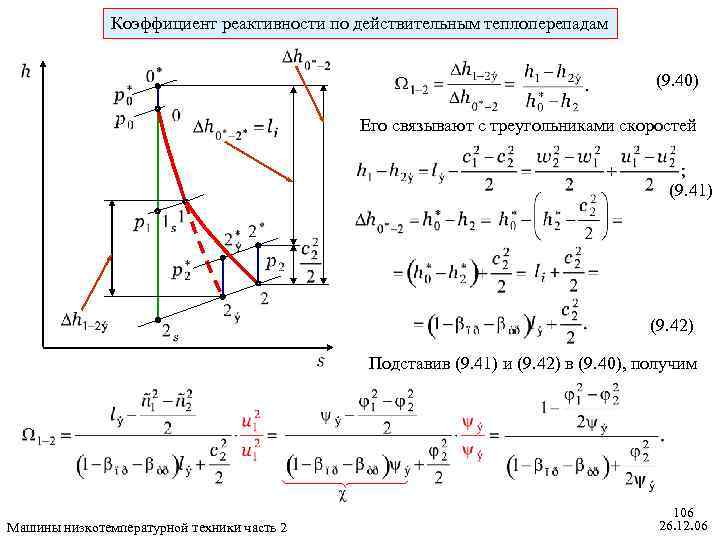Коэффициент реактивности по действительным теплоперепадам (9. 40) Его связывают с треугольниками скоростей (9. 41) (9. 42) Подставив (9. 41) и (9. 42) в (9. 40), получим Машины низкотемпературной техники часть 2 106 26. 12. 06

Окончательно коэффициент реактивности по действительным теплоперепадам принимает такой вид : (9. 43) Кинематический коэффициент реактивности (9. 44) Связь между и . Рассмотрим только числитель в формуле (9. 43) для : (9. 45) Машины низкотемпературной техники часть 2 107 26. 12. 06

Подставив (9. 45) в (9. 43), находим (9. 46) Обычно знаменатель (9. 46) близок к единице Поэтому (9. 46) можно записать так (9. 47) В частном случае при равенстве меридианных составляющих (9. 48) Машины низкотемпературной техники часть 2 108 26. 12. 06

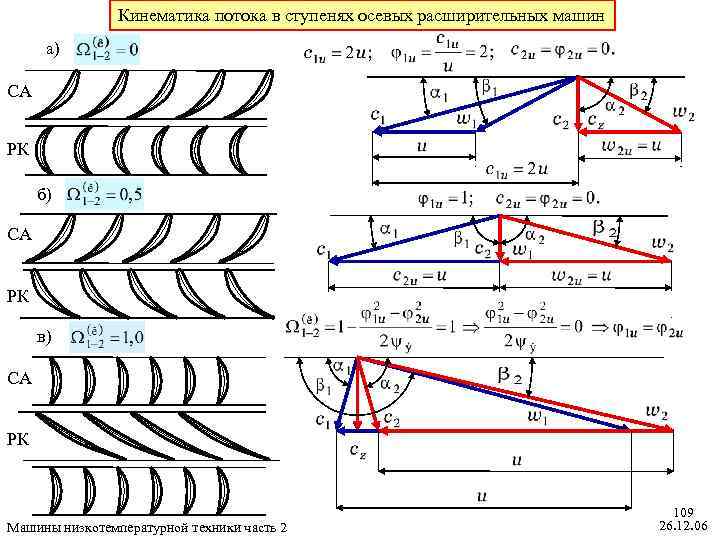Кинематика потока в ступенях осевых расширительных машин а) СА РК б) СА РК в) СА РК Машины низкотемпературной техники часть 2 109 26. 12. 06

Применение ступеней с различными коэффициентами реактивности Машины низкотемпературной техники часть 2 . 110 26. 12. 06

Кинематика потока в реальных ступенях Машины низкотемпературной техники часть 2 111 26. 12. 06

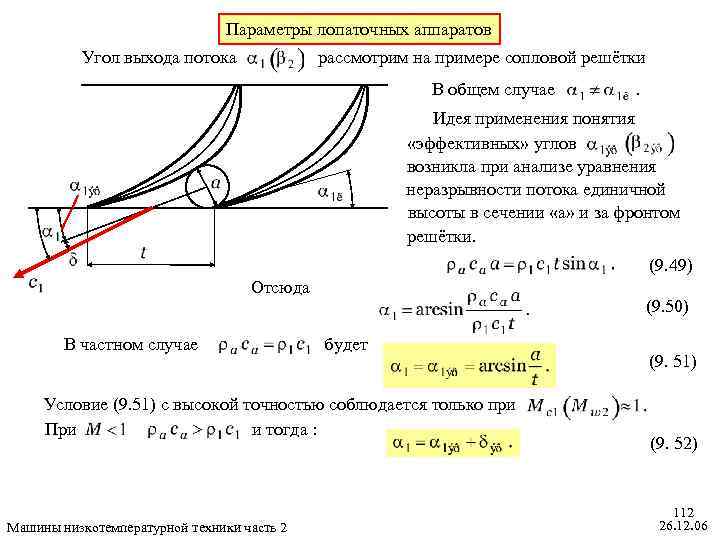Параметры лопаточных аппаратов Угол выхода потока рассмотрим на примере сопловой решётки В общем случае . Идея применения понятия «эффективных» углов возникла при анализе уравнения неразрывности потока единичной высоты в сечении «а» и за фронтом решётки. (9. 49) Отсюда В частном случае (9. 50) будет Условие (9. 51) с высокой точностью соблюдается только при При и тогда : Машины низкотемпературной техники часть 2 (9. 51) (9. 52) 112 26. 12. 06

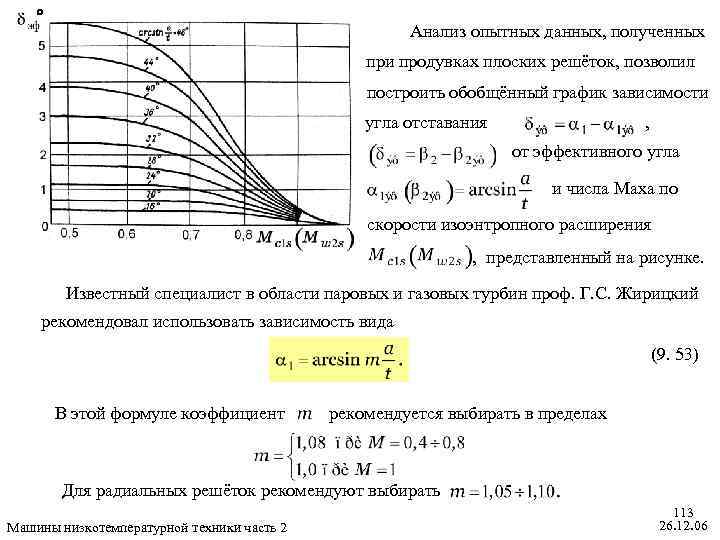Анализ опытных данных, полученных при продувках плоских решёток, позволил построить обобщённый график зависимости угла отставания , от эффективного угла и числа Маха по скорости изоэнтропного расширения , представленный на рисунке. Известный специалист в области паровых и газовых турбин проф. Г. С. Жирицкий рекомендовал использовать зависимость вида (9. 53) В этой формуле коэффициент рекомендуется выбирать в пределах Для радиальных решёток рекомендуют выбирать Машины низкотемпературной техники часть 2 113 26. 12. 06

Расширение потока в косом срезе при сверхкритических перепадах давления При больших перепадах давления скорость в самом узком сечении канала достигает скорости звука и сечение становится критическим. В этом случае уравнение (9. 50) остаётся справедливым, но в числителе должны быть подставлены критические плотность и скорость звука (9. 54) Скорость звука в критическом сечении (9. 55) Как известно из закона обращения воздействия при сверхкритических перепадах давления переход к сверхзвуковым скоростям в геометрическом сопле Лаваля возможен только при увеличении площади потока. Так как площадь потока при выходе из косого среза зависит только от угла выхода , то в зависимости от отношения давлений поток самопроизвольно отклоняется на требуемый угол. Машины низкотемпературной техники часть 2 114 26. 12. 06

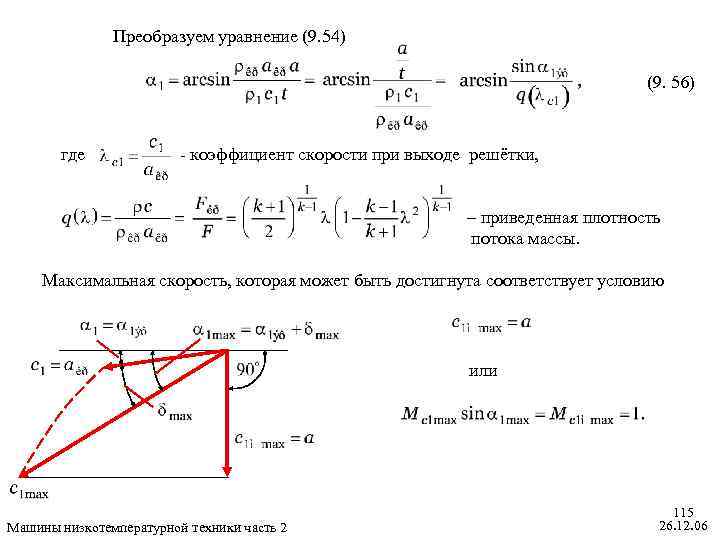Преобразуем уравнение (9. 54) (9. 56) где - коэффициент скорости при выходе решётки, – приведенная плотность потока массы. Максимальная скорость, которая может быть достигнута соответствует условию или Машины низкотемпературной техники часть 2 115 26. 12. 06

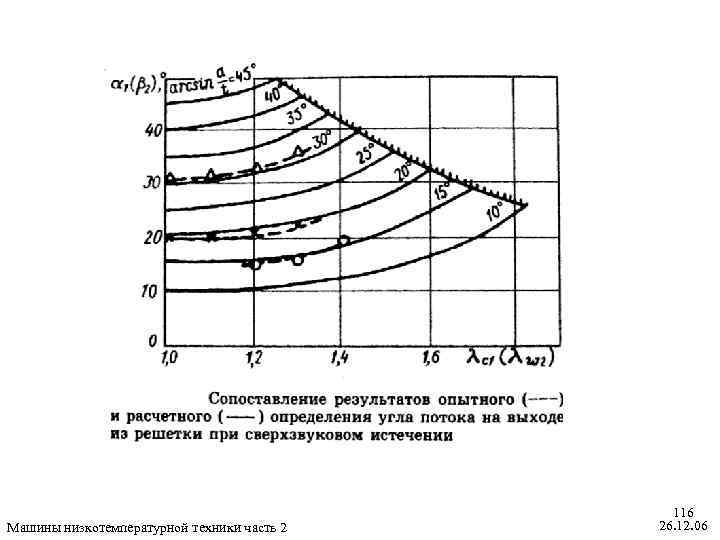Машины низкотемпературной техники часть 2 116 26. 12. 06

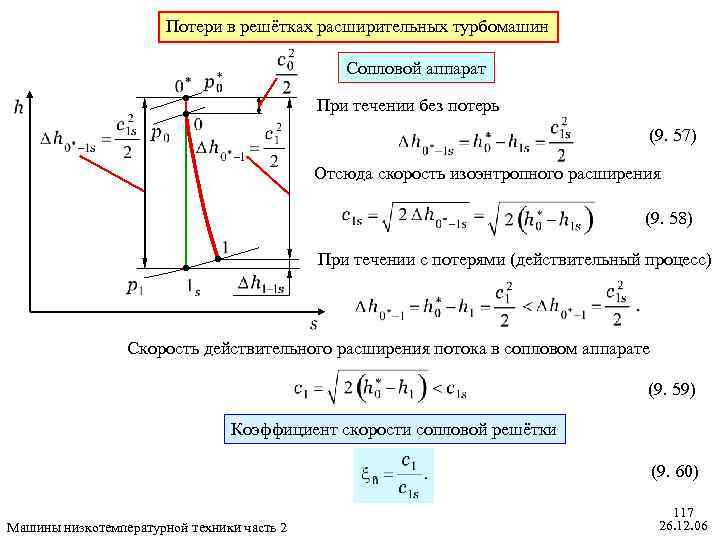Потери в решётках расширительных турбомашин Сопловой аппарат При течении без потерь (9. 57) Отсюда скорость изоэнтропного расширения (9. 58) При течении с потерями (действительный процесс) Скорость действительного расширения потока в сопловом аппарате (9. 59) Коэффициент скорости сопловой решётки (9. 60) Машины низкотемпературной техники часть 2 117 26. 12. 06

Потерянный в сопловой решётке перепад энтальпий (9. 61) Коэффициент потерь сопловой решётки (9. 62) Сопоставляя два последних выражения из (9. 61), найдём соотношение (9. 63) Изоэнтропный к. п. д. сопловой решётки (9. 64) Машины низкотемпературной техники часть 2 118 26. 12. 06

По известным можно найти : и принятых, или найденных из опыта или (9. 65) Для идеального (идеализированного) газа. (9. 66) Изоэнтропный к. п. д. определяется не только энтальпиями, но и температурами Отсюда (9. 67) Статические температура и давление при входе соплового аппарата (9. 68) (9. 69) Показатель политропы расширения в сопловом аппарате (9. 70) Машины низкотемпературной техники часть 2 119 26. 12. 06

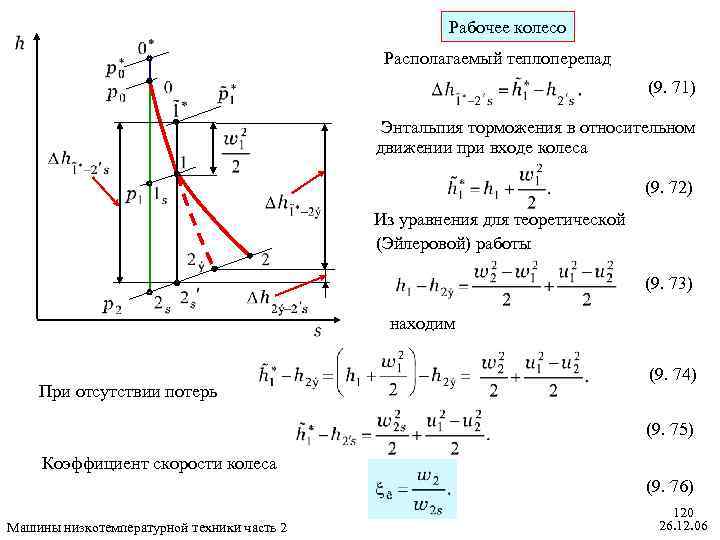Рабочее колесо Располагаемый теплоперепад (9. 71) Энтальпия торможения в относительном движении при входе колеса (9. 72) Из уравнения для теоретической (Эйлеровой) работы (9. 73) находим При отсутствии потерь (9. 74) (9. 75) Коэффициент скорости колеса (9. 76) Машины низкотемпературной техники часть 2 120 26. 12. 06

Потерянный в колесе перепад энтальпий (9. 77) Из двух последних выражений в (9. 77) видим (9. 78) (9. 79) Изоэнтропный к. п. д. колеса Окончательно (9. 80) Из (9. 80) видно, что только для чисто осевых машин, когда равенство Машины низкотемпературной техники часть 2 , справедливо 121 26. 12. 06

В общем случае из (9. 80) найдём или Отсюда (9. 81) Для осевых ступеней Для радиальных ступеней При расчёте находят (9. 72) (9. 82) Машины низкотемпературной техники часть 2 122 26. 12. 06

Для идеального (идеализированного) газа Располагаемый изоэнтропный перепад энтальпий в колесе (9. 83) Изоэнтропный к. п. д. колеса (9. 84) Температуры в начале и конце действительного процесса расширения в колесе (9. 85) (9. 86) Давление торможения при входе колеса в относительном движении (9. 87) Показатель политропы расширения в рабочем колесе (9. 88) Машины низкотемпературной техники часть 2 123 26. 12. 06

Потери в решётках расширительных турбомашин Профильные потери – включают потери на трение в пограничном слое около профиля и кромочные потери из-за конечной толщины выходной кромки профиля. Вторичные потери – включают : ● потери от парного вихря, возникающего из-за взаимодействия пограничных слоёв около профиля и на торцовых стенках ; ● потери от перетекания пограничных слоёв со стороны высокого давления на сторону низкого ; ● потери от нестационарности, вызванной неравномерностью распределения давлений по шагу наличием закромочных следов от лопаток, расположенных выше по потоку ; Волновые потери – из-за скачков уплотнения в сверхзвуковых потоках. Местное превышение скорости звука возникает уже при Коэффициент потерь в решётке (9. 89) Коэффициент профильных потерь Машины низкотемпературной техники часть 2 (9. 90) 124 26. 12. 06

Потери в решётках расширительных турбомашин Машины низкотемпературной техники часть 2 – 2 из 3 125 26. 12. 06

Потери в решётках расширительных турбомашин Машины низкотемпературной техники часть 2 – 3 из 3 126 26. 12. 06

Профилирование лопаточных аппаратов – 1 из 3 ХМ 2006 – параграф 11. 6 стр. 672 -679. ХМ 1997 – параграф 10. 6 стр. 725 -732. Машины низкотемпературной техники часть 2 127 26. 12. 06

Профилирование лопаточных аппаратов Машины низкотемпературной техники часть 2 – 2 из 3 128 26. 12. 06

Профилирование лопаточных аппаратов Машины низкотемпературной техники часть 2 – 3 из 3 129 26. 12. 06

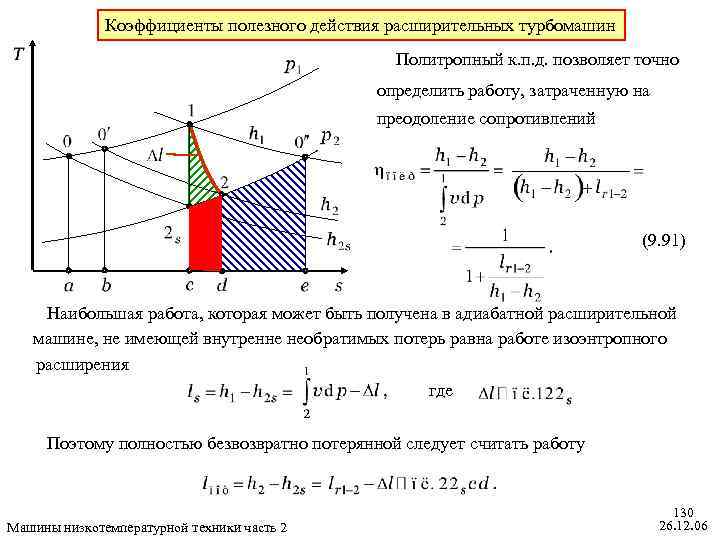Коэффициенты полезного действия расширительных турбомашин Политропный к. п. д. позволяет точно определить работу, затраченную на преодоление сопротивлений (9. 91) Наибольшая работа, которая может быть получена в адиабатной расширительной машине, не имеющей внутренне необратимых потерь равна работе изоэнтропного расширения где Поэтому полностью безвозвратно потерянной следует считать работу Машины низкотемпературной техники часть 2 130 26. 12. 06

Машины низкотемпературной техники часть 2 130 26. 12. 06

Машины низкотемпературной техники часть 2 105 26. 12. 06

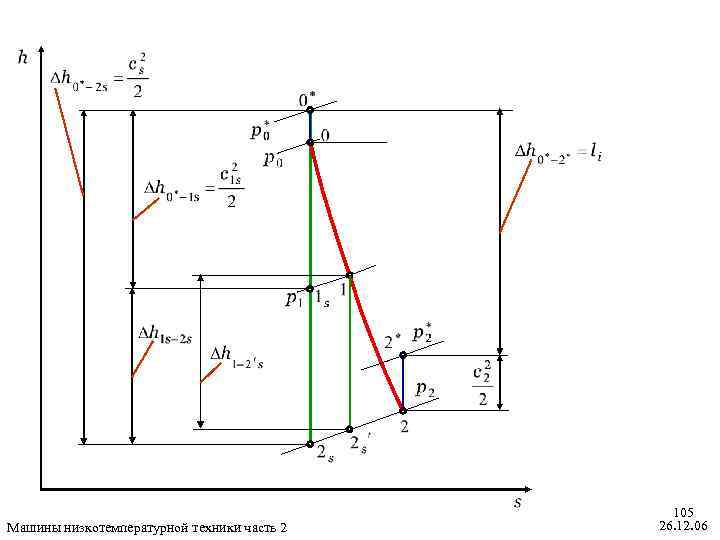Машины низкотемпературной техники часть 2 41 26. 12. 06