Кафедра системного анализа и антикризисного управления УЧЕБНАЯ ДИСЦИПЛИНА

Зарегистрируйтесь, чтобы просмотреть полный документ!

Кафедра системного анализа и антикризисного управления УЧЕБНАЯ ДИСЦИПЛИНА «МОДЕЛИРОВАНИЕ СИСТЕМ» для обучающихся по направлению подготовки (специальности) 230401. 65 - «Прикладная математика»

Тема 2. Моделирование систем на ЭВМ

Лекция 2. 1. Методология имитационного моделирования на ЭВМ Учебные вопросы: 1. 2. 3. 4. 5. 6. Системы массового обслуживания как средство описания элементов вычислительных систем Методы моделирования систем массового обслуживания Основные проблемы реализации метода имитационного моделирования Общая характеристика системы имитационного моделирования Лингвистические средства системы Структура программной модели

Вопросы по планированию эксперимента 1. 2. 3. 4. Вариант 1 Классификация планов по способу перебора факторов. Нарисовать область определения кодированных факторов при двухфакторном эксперименте. Формула для нахождения кодированного значения фактора. Свойство ортогональности матриц ПФЭ. Вариант 2 Классификация планов по цели эксперимента. Нарисовать область определения двухфакторного эксперимента (натуральные факторы). Формула для расчёта интервала варьирования. Свойство симметричности матриц ПФЭ.

1. Системы массового обслуживания как средство описания элементов вычислительных систем

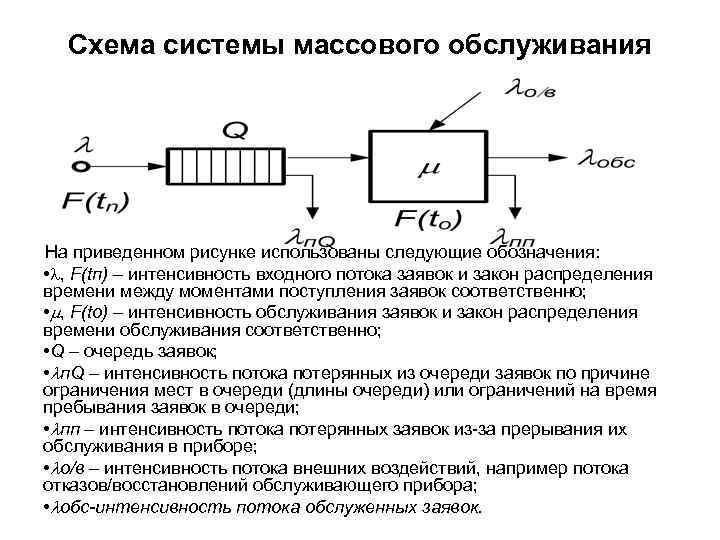
Схема системы массового обслуживания На приведенном рисунке использованы следующие обозначения: • , F(tп) – интенсивность входного потока заявок и закон распределения времени между моментами поступления заявок соответственно; • , F(tо) – интенсивность обслуживания заявок и закон распределения времени обслуживания соответственно; • Q – очередь заявок; • п. Q – интенсивность потока потерянных из очереди заявок по причине ограничения мест в очереди (длины очереди) или ограничений на время пребывания заявок в очереди; • пп – интенсивность потока потерянных заявок из-за прерывания их обслуживания в приборе; • о/в – интенсивность потока внешних воздействий, например потока отказов/восстановлений обслуживающего прибора; • обc-интенсивность потока обслуженных заявок.

Краткая характеристика элементов системы массового обслуживания Входящий (входной) поток заявок. Этот поток представляет собой множество заявок, требующих обслуживания и поступающих на вход СМО в моменты времени ti. Очередь заявок. Она представляет собой множество заявок, ожидающих обслуживания в приборах. Обычно ожидание обусловлено тем, что приборы либо заняты обслуживанием другой заявки, либо находятся в состоянии отказа. Обслуживающий прибор. Это устройство или совокупность устройств, выполняющих операции по обслуживанию заявок. Устройство обслуживания также называют каналом. Принято считать, что в конкретный момент времени канал может быть свободным или обслуживать только одну заявку. Выходной поток. Это поток заявок, покидающих СМО в обслуженном состоянии, или заявок, не получивших обслуживания по некоторым причинам (в силу ограничений на длину или время пребывания в очереди, из-за реализации абсолютных приоритетов в обслуживании заявок и др. ). Поток внешних воздействий. Им называют поток заявок, имитирующих события отказов и восстановлений каналов обслуживания по причине конечной надежности технических устройств, воздействия помех и т. п. Устройство управления (на рисунке не показано). Это устройство обеспечивает поддержание заданного режима функционирования СМО. В его функции входит реализация различных алгоритмов управления, характерных для моделируемых объектов, например, порядок выбора маршрута на сети.

Характеристики входящего потока заявок • интенсивность поступления заявок ; • закон распределения времени поступления заявок F(tп); • приоритет заявок Pr; • параметры заявок, определяющие длительность их обслуживания tо; • адрес источника заявок Аи; • адрес получателя заявок Ап и др.

Интенсивность поступления заявок определяется средним числом заявок в единицу времени. Если входящий поток - стационарный, то =Const (интенсивность является постоянной величиной и не изменяется во времени); - не стационарный, то =f(t) (интенсивность может изменяться во времени).

Виды (законы) распределения времени между моментами поступления заявок t 1) регулярное, при котором t=Const, т. е. заявки поступают через одинаковые промежутки времени; 2) равномерное в диапазоне [a, b]; 3) экспоненциальное; 4) нормальное.

Функция плотности равномерного распределения

Функция плотности экспоненциального распределения

Функция плотности нормального распределения где m-математическое ожидание t; -среднеквадратическое отклонение этой величины от математического ожидания.

Наибольшее практическое применение при моделировании входящего потока заявок нашел экспоненциальный закон в силу следующих причин: 1. он создает наиболее тяжелый режим обслуживания заявок в СМО и Се. МО; 2. при большом числе источников заявок суммарный поток стремится к простейшему, имеющему экспоненциальное распределение вне зависимости от законов распределения, свойственных отдельным источникам. В общем случае в СМО и Се. МО поступает неоднородный поток заявок. В таком потоке заявки различаются по приоритетам, длине или времени обслуживания, адресам источников и получателей и другим параметрам.

Свойства простейшего (пуассоновского) потока 1. Стационарность означает, что вероятность поступления определенного количества заявок в течение определенного интервала времени зависит лишь от величины этого интервала и не зависит от его положения на оси времени. Стационарность наблюдается при неизменности условий, порождающих поток заявок. В частности, интенсивность стационарного потока должна быть постоянной, т. е. в среднем на интервалах равной длины должно быть одинаковое количество заявок. 2. Ординарность означает, что вероятность одновременного поступления двух и более заявок равна нулю. 3. Отсутствия последействия означает независимость поступления заявок друг от друга. Это свойство потока заявок вытекает из независимости числа заявок, поступивших за некоторый интервал времени, от того, как они поступали до этого времени.

Характеристики очереди заявок • максимальная длина очереди; • допустимое время пребывания заявки в очереди; • дисциплина постановки заявок в очередь и выбора из нее (FIFO, LIFO, Pr). FIFO- «первым пришел-первым обслужен» ; LIFO - «последним пришел-первым обслужен» ; Pr- приоритет.

Характеристики обслуживающего прибора • число каналов (одноканальные и многоканальные СМО); • надежность каналов (абсолютно надежные и с конечной надежностью); • интенсивность обслуживания (число заявок в единицу времени); • закон распределения времени обслуживания заявок F(t 0); • дисциплина обслуживания (без прерываний, с прерываниями).

2. Методы моделирования систем массового обслуживания

Постановка задачи исследования реальной системы с помощью СМО Дано (известно): 1. Структура реальной системы. 2. Параметры элементов. 3. Порядок функционирования системы. Требуется оценить: Эффективность функционирования системы в заданном интервале времени T.

Методы, используемые для построения моделей, базирующихся на использовании СМО аналитические статистические (имитационные) При аналитическом моделировании используется математический аппарат теории вероятностей, дифференциальных уравнений, производящих функций, марковских случайных процессов и другие. При этом следует отметить, что с помощью аналитических методов удается построить только модели простых систем. Аналитическое моделирование сложных систем требует введения существенных ограничений и допущений, что в итоге снижает адекватность моделей. Имитационное моделирование основано на следующей идее. Для случайных величин (параметров исследуемой системы и среды) по жребию, в соответствии с законами их распределения, выбираются их значения. При полученных значениях строится модель детерминированного процесса (что существенно проще построения модели случайного процесса). На этой модели вычисляется значение интересующего показателя. Такое однократное воспроизведение (имитация) функционирующей системы, называется статистическим испытанием. Эта процедура многократно повторяется. После проведения серии испытаний результирующие данные подвергаются статистической обработке.

Постановка задачи исследования одноканальной СМО Дано: одноканальная СМО, для которой известны: плотность распределения времени ожидания заявки в очереди f 1(tож); плотность распределения времени обслуживания заявки прибором f 2(tобс). Требуется определить среднее время пребывания заявки в СМО.

Аналитическая модель где tобс=tпр-tож

Имитационная модель 1) строится модель детерминированного процесса в виде tпрi=tожi+tобсi, i=1, 2, …, n. 2) по жребию в соответствии с законами распределения f 1(tож) и f 2(tобс) n раз выбираются значения tожi и tобсi и вычисляются значения tпрi. Получается последовательность значений tпр1, tпр2, …, tпрn. 3) на основе полученных статистических данных вычисляется искомая величина

3. Основные проблемы реализации метода имитационного моделирования

Основные проблемы реализации метода имитационного моделирования 1) формирование случайных чисел, распределенных по заданному закону распределения; 2) определение числа испытаний, обеспечивающих заданные точность и достоверность моделирования; 3) построение алгоритмов, реализующих процесс моделирования.

Формирование случайных чисел, распределенных по заданному закону распределения Функция плотности ДСЧ с равномерным распределением

Формирование случайных чисел, распределенных по экспоненциальному закону

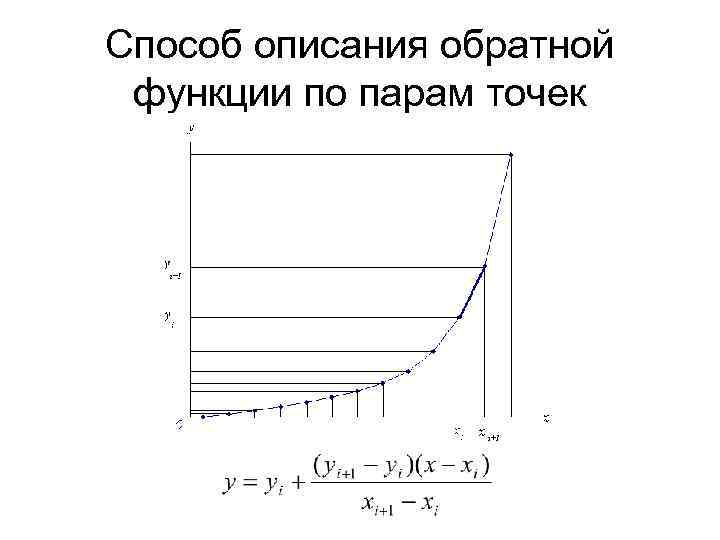
Способ описания обратной функции по парам точек

Определение числа испытаний, обеспечивающих заданные точность и достоверность моделирования Задача определения числа испытаний решается на основе предельной теоремы, согласно которой отклонение среднего значения случайной величины x от его математического ожидания распределено по нормальному закону с математическим ожиданием m(x)=0 и дисперсией где (x) – среднеквадратичное отклонение случайной величины x, N – число испытаний. В результате статистических испытаний находится оценка требуемого параметра. В силу случайных причин эта оценка отличается от истинного значения. Это отличие определяется точностью и достоверностью оценки.

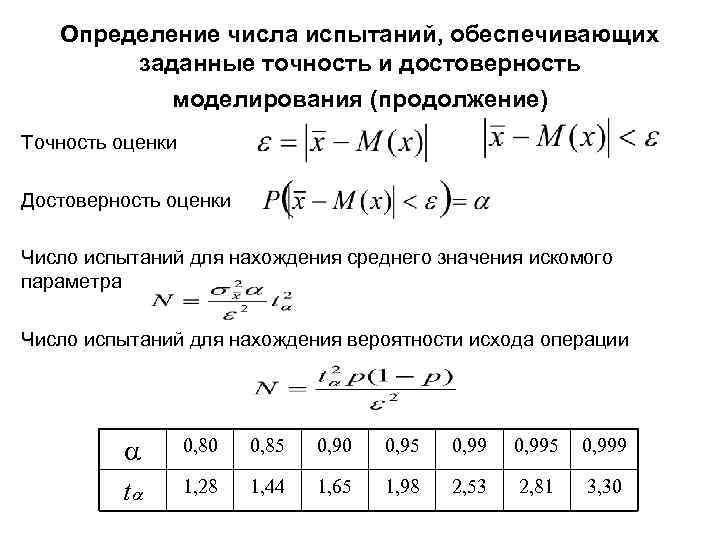
Определение числа испытаний, обеспечивающих заданные точность и достоверность моделирования (продолжение) Точность оценки Достоверность оценки Число испытаний для нахождения среднего значения искомого параметра Число испытаний для нахождения вероятности исхода операции t 0, 80 0, 85 0, 90 0, 95 0, 995 0, 999 1, 28 1, 44 1, 65 1, 98 2, 53 2, 81 3, 30

Определение числа испытаний, обеспечивающих заданные точность и достоверность моделирования (продолжение) Выражение для достоверности характеризует устойчивость результатов эксперимента и трактуется следующим образом: если для оценки параметра М(x) систематически использовать величину , то в среднем на каждый N применений этого правила в Nα случаях случайная величина будет отличаться от M(x) меньше чем на , в N(1 -α) случаях разность между и М(x) будет больше или равна . - оценка математического ожидания искомого параметра; M(x) – математическое ожидание искомого параметра; - среднеквадратическое отклонение математического ожидания искомого параметра; tα -значение аргумента функции Лапласа, при котором вероятность попадания случайной величины в интервал (- tα , tα ) равна α.

Определение числа испытаний, обеспечивающих заданные точность и достоверность моделирования (окончание) При определении необходимого числа испытаний . Величина должна быть известна, хотя бы ориентировочно. Если это требование не выполняется, то можно воспользоваться следующими приемами: 1) по определенному значению размаха колебаний случайной величины как 2) по пробной серии испытаний находится оценка среднеквадратичного отклонения Тогда Если целью моделирования является нахождение вероятности исхода операции, то требуемое число испытаний должно быть , где p – априорное значение вероятности, которое можно определить предварительным испытанием на модели. Для случая, когда значение p вычислить не удается, можно воспользоваться упрощенной формулой для наихудшего случая (p=0, 5). Тогда.

Построение алгоритмов, реализующих процесс моделирования Алгоритм моделирования по принципу особых состояний (событий) Алгоритм моделирования по принципу t

Алгоритм моделирования по принципу особых состояний (событий). В качестве особых событий выделяют: - поступление заявки в систему; - освобождение элемента после обслуживания заявки; - завершение моделирования и т. п. В общем случае в системе могут быть выделены события и других типов, например возникновение отказа устройства в процессе обслуживания заявки и завершение восстановления устройства после отказа. Процесс имитации функционирования системы развивается во времени с использованием управляющих последовательностей, определяемых по функциям распределения вероятностей исходных данных путем проведения случайных испытаний.

Алгоритм моделирования по принципу особых состояний (событий) 1) определяется событие с минимальным временем – наиболее раннее событие; 2) модельному времени присваивается значение времени наступления наиболее раннего события; 3) определяется тип события; 4) в зависимости от типа события предпринимаются действия, направленные на загрузку устройств и продвижение заявок в соответствии с алгоритмами их обработки, и вычисляются моменты наступления будущих событий; эти действия называют реакцией модели на события; 5) перечисленные действия повторяются до истечения времени моделирования.

Алгоритм моделирования по принципу особых состояний (событий) (окончание) Цикл повторяется до достижения конца моделирования, после чего завершается обработка статистики, и выводятся результаты. На этом заканчивается модельный эксперимент. В системе-оригинале могут протекать одновременно несколько процессов. Это приводит к тому, что в один и тот же момент времени в системе может возникнуть несколько особых событий. При моделировании на однопроцессорной ЭВМ эти ситуации разрешаются таким образом: последовательно в установленном порядке реализуются реакции на все одновременно возникшие ситуации без продвижения модельного времени. Это называется псевдопараллельной имитацией нескольких процессов.

Алгоритм моделирования по принципу t. Основные операции, с помощью которых имитируется функционирование системы, выполняются в цикле. Функционирование системы отслеживается по последовательной смене состояний zi (t). Для этого модельному времени дается некоторое приращение t. Затем по вектору текущих состояний определяются новые состояния zi(t+ t), которые становятся текущими. Для определения новых состояний по текущим в формализованном описании системы должны существовать необходимые математические зависимости. Такой цикл продолжается до тех пор, пока текущее модельное время меньше заданного времени моделирования Тm. По ходу имитации измеряются, фиксируются и обрабатываются требуемые выходные характеристики. При t>=Тm завершается обработка измерений и выводятся результаты моделирования. При моделировании стохастических систем вместо новых состояний вычисляются распределения вероятностей для возможных состояний. Конкретные значения вектора текущего состояния определяются по результатам случайных испытаний. В результате проведения имитационного эксперимента получается одна из возможных реализаций случайного многомерного процесса в заданном интервале времени (t 0, Tm). Моделирующий алгоритм, основанный на принципе t, применим для более широкого круга систем, чем алгоритм, построенный по принципу особых состояний. Однако при его реализации возникают проблемы с определением величины t.

4. Общая характеристика системы имитационного моделирования

Имитационная модель представляет собой систему, отображающую структуру и функционирование исходного объекта в виде алгоритма, связывающего входные и выходные переменные, принятые в качестве характеристик исследуемого объекта. Имитационные модели реализуются программно с использованием различных языков. Одним из наиболее распространенных языков, специально предназначаемых для построения имитационных моделей, является GPSS (General Purpose Simulation System –система имитационного моделирования общего назначения). В состав GPSS входят следующие типы объектов: транзакты, блоки, списки, устройства, памяти, логические ключи, очереди, таблицы, ячейки, функции, переменные.

Любую модель на языке GPSS можно представить в виде комбинации компонентов, взятых из числа названных объектов. Модель имеет три уровня представления: 1) верхний уровень, определяемый комбинацией основных функциональных объектов устройств, памятей, ключей, очередей; 2) средний уровень, представляемый схемой из типовых блоков, между которыми перемещаются транзакты; 3) нижний уровень – уровень физической реализации GPSS в виде программ и наборов данных, составляющих основу симулятора GPSS. Разработчик конструирует модель из блоков, прибегая, как правило, к наглядной форме ее отображения в виде блок-схемы. Для удобства графического представления модели каждый блок GPSS имеет принятое стандартное обозначение. Построенная схема является одновременно программой на языке GPSS.

Категории и типы объектов GPSS Категории объектов Типы объектов Операционная Блоки (операторы) Аппаратная Памяти (накопители, многоканальные устройства) Динамическая Транзакты (заявки) Вычислительная Переменные (арифметические и булевы) и функции Статистическая Очереди, таблицы Запоминающая Ячейки памяти Группирующая Группы (семейства) транзактов, списки, создаваемые пользователями

5. Лингвистические средства системы

Алфавит GPSS состоит из: - латинских букв (A–Z, a–z); - цифр (0– 9) и специальных символов. (Буквы кириллицы могут использоваться лишь в комментариях). Типы используемых чисел: целые и действительные. Лексика языка состоит из: - кодов операций, - идентификаторов; - стандартных числовых атрибутов (СЧА). Идентификаторы используются для формирования имен объектов. Они могут задаваться либо в виде целого числа, либо в виде последовательности алфавитно-цифровых символов (3 -5 символов, из них три первые – буквы). В процессе моделирования автоматически регистрируется информация о различных объектах модели. Доступ к этой информации осуществляется с помощью СЧА. Для указания объекта, о котором необходимо получить информацию, за каждым СЧА указывается числовое или символическое имя объекта.

Формат операторов GPSS [Метка] _ Операция _ Операнды [; Комментарии] Поле операндов: A, B, C, D, E, F, G

Метка (если она имеется) должна размещаться с первой колонки и содержать не более пяти алфавитно-цифровых символов, начинающихся с буквы. Звездочка (*) в первой колонке означает строку комментария. Поле операции содержит название блока или служебного оператора (карты). Это поле может начинаться со второй колонки и должно быть отделено от метки пробелом. Длина поля операции не менее четырех символов (начальные символы блоков или карт). Поле операндов отделяют от поля операции пробелом. Между операндами должны стоять запятые. В поле операндов может размещаться до 7 позиционных операндов с условными именами A, B, C, D, E, F, G. Если один или несколько операндов отсутствуют, то это отмечается соответствующим количеством запятых. При отсутствии операнда выполняются действия, предусмотренные механизмом умолчания. Точка с запятой означает начало комментария в строке.

6. Структура программной модели

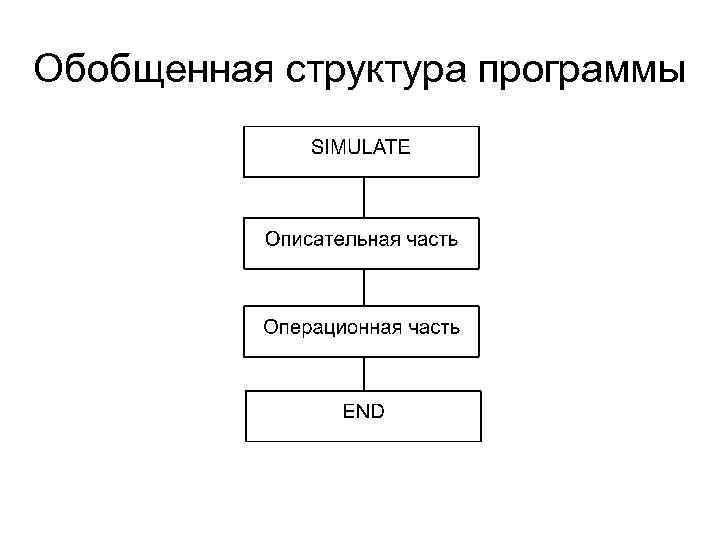
Обобщенная структура программы

В описательной части представляются следующие описания объектов модели: - функции; - памяти; - таблицы; - переменные. Такие типы объектов, как устройства, транзакты, ячейки памяти, списки, в описательной части не присутствуют, т. к. для них определены строго фиксированные участки оперативной памяти. В операционной части располагаются блоки, такие как источники динамических объектов (транзактов) и операторы, задающие логику функционирования модели, т. е. определяющие траекторию движения транзактов между объектами других категорий. Каждый блок GPSS имеет входы и выходы, с помощью которых осуществляется их связь в модели. Существуют два особых блока: GENERATE, имеющий только выход, и TERMINATE, имеющий только вход. Через блок GENERATE транзакты вводятся в модель. Блок TERMINATE удаляет транзакты из модели.

Пример построения модели на языке GPSS SIMULATE 1 FUNCTION RN$1, C 13 0, 0/0. 1, 0. 104/0. 2, 0. 222/0. 3, 0. 357/0. 4, 0. 511/ 0. 5, 0. 693/0. 6, 0. 915/0. 7, 1. 304/0. 8, 1. 610/ 0. 9, 2. 303/0. 97, 3. 507/0. 995, 5. 298/0. 999, 7 1 VARIABLE 3600000/X$1 2 FVARIABLE P$1*FN$1*1000/X$3 1 TABLE M$1, 0, 1000, 20 GENERATE V$1, FN$1 ASSIGN 1, X$2 QUEUE 1 SEIZE 1 DEPART 1 ADVANCE V$2 RELEASE 1 TABULATE 1 TERMINATE 1 INITIAL X$1, 1000, X$2, 30000 INITIAL X$3, 56000 START 1000 END

FUNCTION RN$1, C 13 RN-генератор равномерно распределенных случайных чисел; $-символическое имя; С 13, С- непрерывная функция, 13 - число значений случайной величины; VARIABLE-фиксированная точка; FVARIABLE- плавающая точка; n TABLE A, B, C, D -n –номер (имя) таблицы; -А- табулируемый (СЧА) стандартный числовой атрибут (аргумент таблицы); -В- верхняя граница первого интервала; -С- ширина интервала; -D- число интервалов. Блок TABLE является описательным, через него транзакты не проходят. Для заполнения таблицы необходимо, чтобы транзакты прошли блок TABULATE А, В -А- номер (имя) таблицы; -В- число добавляемых соответствующий интервал единиц (по умолчанию -1)

Через блок GENERATE транзакты вводятся в модель; Блок TERMINATE удаляет транзакты из модели; ASSIGN A, B ASSIGN - назначить Данные из операнда В фиксируются в параметре, имя которого задается в А. В результате предыдущее значение параметра меняется на новое; ASSIGN 1, X$2 - значение первого параметра транзакта становиться равным X$2; QUEUE А, В DEPART A, B QUEUE - встать в очередь DEPART- покинуть очередь -А –имя регистратора (по умолчанию-ошибка); -В – число элементов, на которое изменяется значение счетчика содержимого очереди (по умолчанию-ошибка). Блоки QUEUE, DEPART – определяют только необходимость сбора статистики по данной очереди: их отсутствие не влияет на реальное существование и динамику очереди.

SEIZE A SEIZE –занять прибор А – символическое или числовое имя занимаемого прибора; RELEASE A RELEASE-освободить прибор А - символическое или числовое имя освобождаемого прибора; ADVANCE А, В ADVANCE – задержка заявки в устройстве, захваченном заявкой А – среднее время задержки (константа, если В не задано) В- разброс относительно среднего значения, должен быть меньше или равен А; INITIAL A, B (Пример: INITIAL X$3, 56000 –ячейки с именем 3, присваивается начальное значение 56000) INITIAL – инициализировать А – имя сохраняемой величины В- начальное значение (по умолчанию -1); Оператор START- обычно находится в конце программы, после обнаружение этого оператора интерпретатором начинается моделирование (например: START 1000 - задание числа заявок)

Скачать презентацию Кафедра системного анализа и антикризисного управления УЧЕБНАЯ ДИСЦИПЛИНА

Моделирование систем. Слайды к лекции 03 (Л4).ppt

Количество слайдов: 52