Кафедра медицинской и биологической физики Тема Элементы теории

Кафедра медицинской и биологической физики Тема: Элементы теории вероятностей. Законы распределения случайных величин. лекция № 2 для студентов 1 курса, обучающихся по специальности 060103 - Педиатрия К. п. н. , доцент Шилина Н. Г. Красноярск, 2012

План лекции 1. Случайное событие. Вероятность события. 2. Теоремы сложения и умножения вероятностей. Формула полной вероятности. Формула Байеса. 3. Законы распределения случайных величин 4. Основные характеристики дискретных и непрерывных случайных величин 5. Правила группировки данных

Понятие случайного события События (явления) подразделяют на три вида: oдостоверные, oневозможные, oслучайные.

Достоверное событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий. Примером достоверных событий может быть и наступление времени 15. 00 после 14. 59, и образование кристаллов солей после испарения соленой воды и др.

Невозможное событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий. В качестве невозможных событий можно назвать и образование устойчивого следа в воздухе после полета птицы, и самопроизвольное преобразование гранита в воду, и притяжение магнитом полиэтилена и др.

Случайное событие, которое при осуществлении совокупности условий может либо произойти, либо не произойти. Примерами случайных событий являются выбор конкретной конфеты из коробки, содержащей одинаковые конфеты, перемещение броуновской частицы, бросание монетки с целью получить на верхней стороне “орел” или “решка” и т. д.

Несовместные события если появление одного из них исключает появление других событий в одном и том же испытании. В качестве примера несовместных событий укажем розыгрыш в лотерею, где событие выигрыша всегда несовместно с проигрышем.

Независимые события если появление одного события не изменяет вероятности другого события. В качестве примера независимых событий укажем бросание подряд 2 монеток с целью получить на верхней стороне “орел” или “решка”.

Полная группа событий Несколько случайных несовместных событий образуют полную группу, если в результате испытания появится только одно из них. Примером полной группы - выбор случайной цифры в забытом телефонном номере, который состоит из 10 несовместных событий - десятичных цифр 0, 1, 2, 3 … 9.

Противоположные события Если полная группа состоит только из двух событий, то такие события обычно называют противоположными и обозначают A - исходное событие, А противоположное. Например, стрелок выстрелил по мишени. Обязательно произойдет одно из двух событий: попадание, промах.

Классическое определение вероятности события Вероятностью события A называют отношение числа благоприятствующих этому событию элементарных событий к общему числу всех равновозможных несовместных элементарных событий, образующих полную группу. где m- число элементарных событий, благоприятствующих событию A, n- число всех возможных элементарных событий.

Числовые значения вероятностей o вероятность достоверного события равна P(A)=n/n=1. o вероятность невозможного события равна P(A)=0/n=0. o вероятность случайного события заключена в пределах 0<P(A)<1.

Относительная частота события A отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. m - число испытаний, где проявилось событие A, n - число всех испытаний.

Статистическое определение вероятности события Вероятностью события A называют число, к которому стремиться относительная частота события A при увеличении количества испытаний.

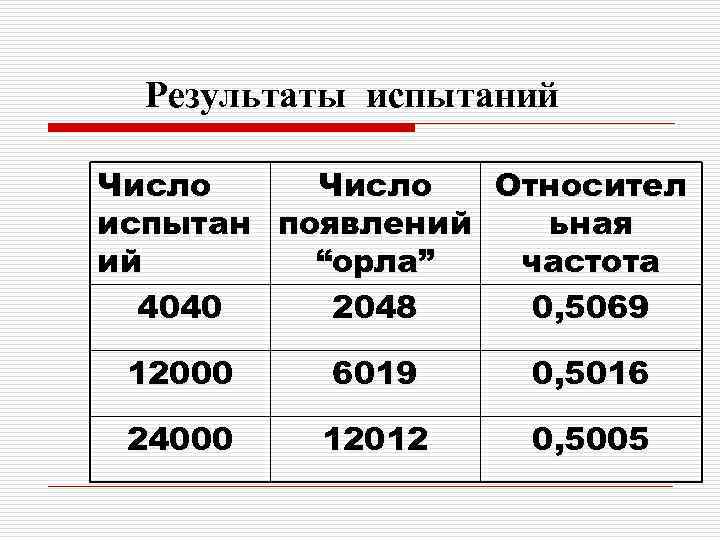
Результаты испытаний Число Относител испытан появлений ьная ий “орла” частота 4040 2048 0, 5069 12000 6019 0, 5016 24000 12012 0, 5005

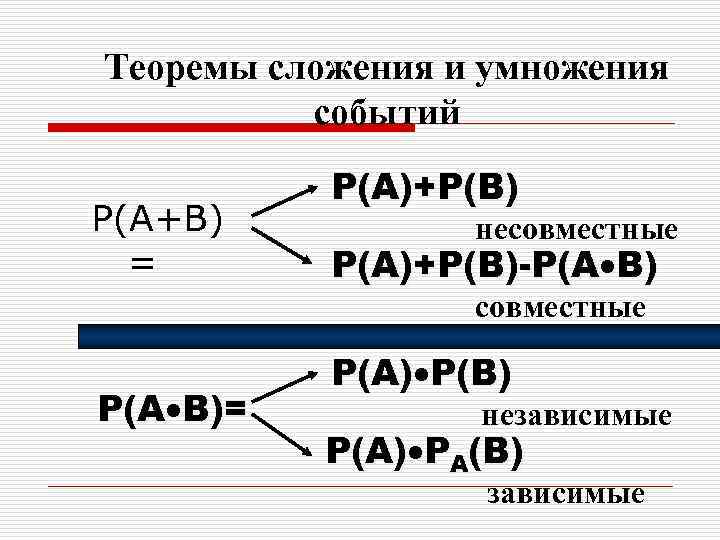
Теоремы сложения и умножения событий P(A+B) = P(A)+P(B) несовместные P(A)+P(B)-P(A B) совместные P(A B)= P(A) P(B) независимые P(A) PA(B) зависимые

Теорема сложения несовместных событий Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: P(A+B)=P(A)+P(B) Следствие. сумма вероятностей несовместных событий, образующих полную группу, равна 1. Для двух противоположных событий P(A)+P(A)=1

Теорема сложения совместных событий Вероятность появления одного из двух совместных событий, безразлично какого, равна сумме вероятностей этих событий минус вероятность их совместного появления: P(A+B)=P(A)+P(B)-P(A B)

Теорема умножения независимых событий Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий: P(A B)=P(A) P(B)

Теорема умножения независимых событий (пример) Найти вероятность совместного появления “орла” при одном бросании двух монет. Решение. Вероятность появления “орла” для первой монеты P(A)=0, 5. Вероятность появления “орла” для второй монеты P(B)=0, 5. Так как события A и B независимые, то: P(A·B)=P(A) · P(B)=0, 5 · 0, 5=0, 25.

Теорема умножения зависимых событий Вероятность совместного появления двух зависимых событий равна произведению вероятности одно из них на условную вероятность другого события, вычисленную в предположении, что первое событие уже произошло: P(A B)=P(A) PA(B)

Условная вероятность PA(B) вероятность события B, вычисленную в предположении, что событие A уже наступило.

Теорема умножения зависимых событий (пример) В коробке имеется две израсходованные и восемь новых ампул. Найдите вероятность того, что подряд будут взяты одна новая и одна израсходованная ампула. Решение. Вероятность события A (извлечь новую ампулу) равна P(A)=8/10=0, 8. Вероятность события B (извлечь пустую ампулу после извлечения новой) равна PA(B)=2/9 0, 222. Искомая вероятность P(A · B)=P(A) · PA(B) = 0, 8· 0, 222 0, 178.

Формула полной вероятности Вероятность события A, которое может наступить лишь при условии появления одного из несовместных событий B 1, B 2 , B 3, … , Bn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A: P(A)=P(B 1)PB 1(A)+ P(B 2)PB 2(A)+… +P(Bn)PBn(A)

Формула полной вероятности P(A)=P(B 1)PB 1(A)+ P(B 2)PB 2(A)+… +P(Bn)PBn(A) краткая запись

Формула Байеса (переоценки вероятности) Пусть событие A может наступить лишь при условии появления одного из несовместных событий B 1, B 2 , B 3, … , Bn , образующих полную группу. Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами. Произведено испытание, в результате которого появилось событие A. Как же изменились вероятности гипотез (в связи с тем, что событие A уже наступило)?

Формула Байеса i=1, 2, …, n

Формула Бернулли Вероятность одного события B, состоящего в том, что в n независимых испытаниях событие A наступит k раз и не наступит n-k раз, по теореме умножения вероятностей независимых событий равна pk(1 -p)n-k. Но таких событий B может быть столько, сколько существует вариантов выбора k элементов из n ( или число сочетаний) q=1 -p

Формула Бернулли (пример) Требуется узнать какова вероятность выпадения “орла” ровно 4 раза при подбрасывании монеты 6 раз? Решение. Считаем каждое подбрасывание монеты независимым. Очевидно, что p=0, 5, а q=0, 5:

Виды случайных величин Случайная величина – это такая величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее какое именно. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ ДИСКРЕТНЫЕ НЕПРЕРЫВНЫЕ

Дискретная и непрерывная случайные величины (понятие) Дискретная случайная величина – это такая величина, которая может принимать только конечное или счетное множество значений. Непрерывная случайная величина – это такая величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка.

Закон распределения случайной величины всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Может задаваться в виде: • таблицы • графика • формулы (аналитически).

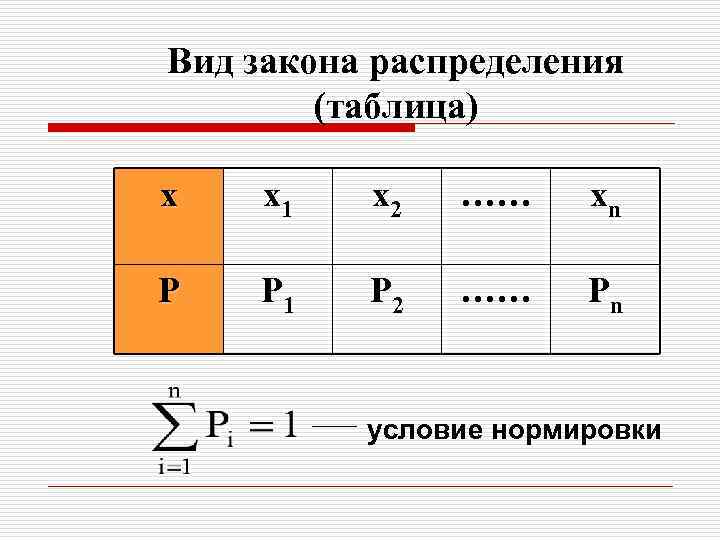
Вид закона распределения (таблица) х х1 х2 …… хn Р Р 1 Р 2 …… Рn условие нормировки

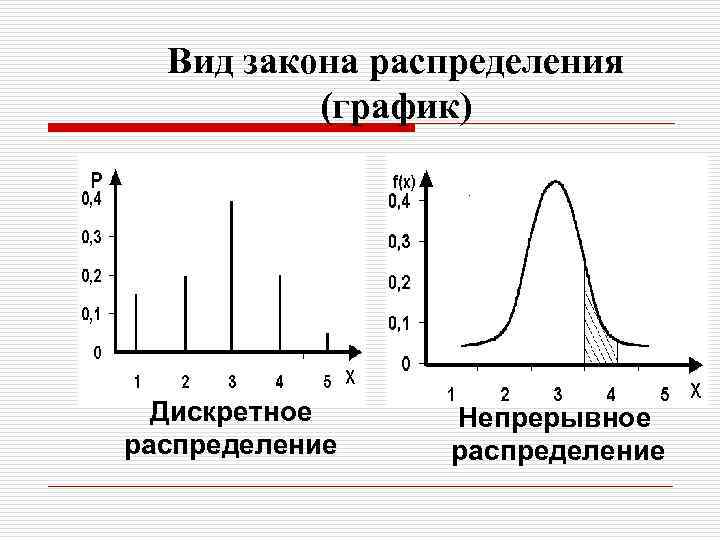
Вид закона распределения (график) Дискретное распределение Непрерывное распределение

Вид закона распределения (формула) Функция плотности вероятностей распределения частоты пульса у студентов 1 курса Крас. ГМУ

Основные характеристики дискретных случайных величин • Математическое ожидание • Дисперсия • Среднее квадратическое отклонение

Математическое ожидание дискретной случайной величины (среднее значение) равно сумме произведений значений, принимаемых этой величиной, на соответствующие им вероятности: М(x)=x 1 Р 1 + x 2 Р 2 +. . . + xn. Pn =

Дисперсия дискретной случайной величины это математическое ожидание квадрата соответствующего отклонения случайной величины x от ее математического ожидания: D(x) = M [x – M(x)]2 или

Среднее квадратическое отклонение

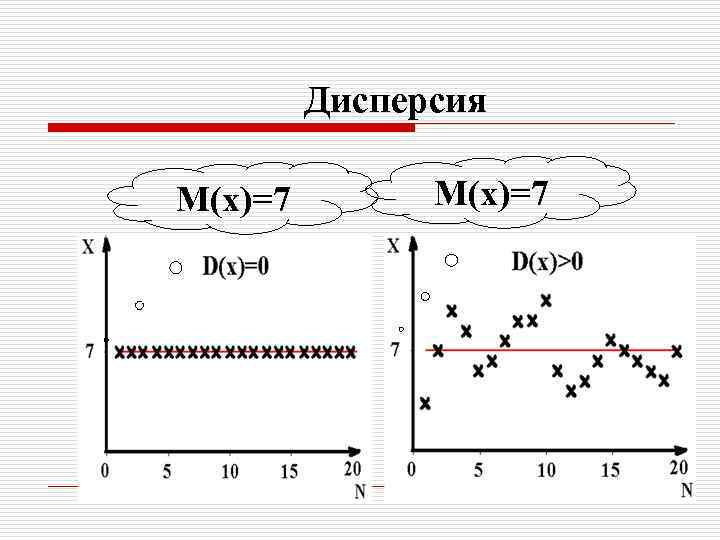
Дисперсия M(x)=7

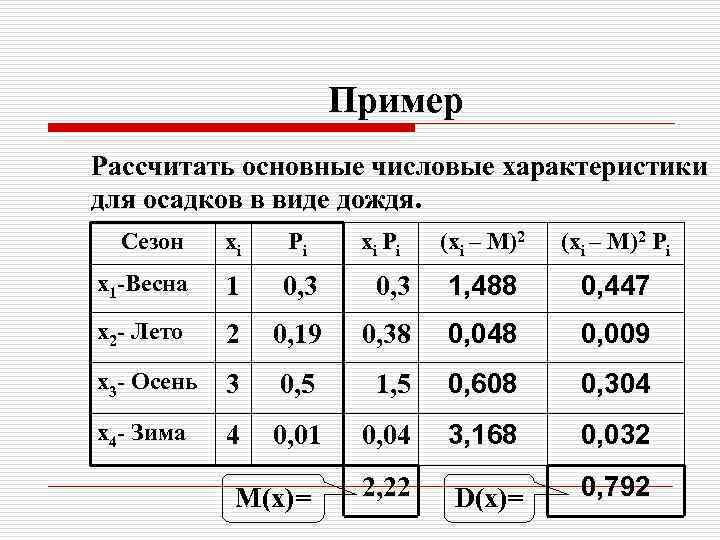
Пример Рассчитать основные числовые характеристики для осадков в виде дождя. Сезон xi Pi x 1 -Весна 1 0, 3 x 2 - Лето 2 x 3 - Осень x 4 - Зима (xi – M)2 Pi 0, 3 1, 488 0, 447 0, 19 0, 38 0, 048 0, 009 3 0, 5 1, 5 0, 608 0, 304 4 0, 01 0, 04 3, 168 0, 032 2, 22 D(x)= 0, 792 M(x)= xi Pi

Расчет примера o М(x)=1 0, 3+2 0, 19+3 0, 5+4 0, 01=2, 22 o D(x)=(1 -2, 22)2∙ 0, 3+(2 -2, 22)2∙ 0, 19+ (3 -2, 22)2∙ 0, 5+(4 -2, 22)2∙ 0, 01= 0, 792 o (x)= =0, 890

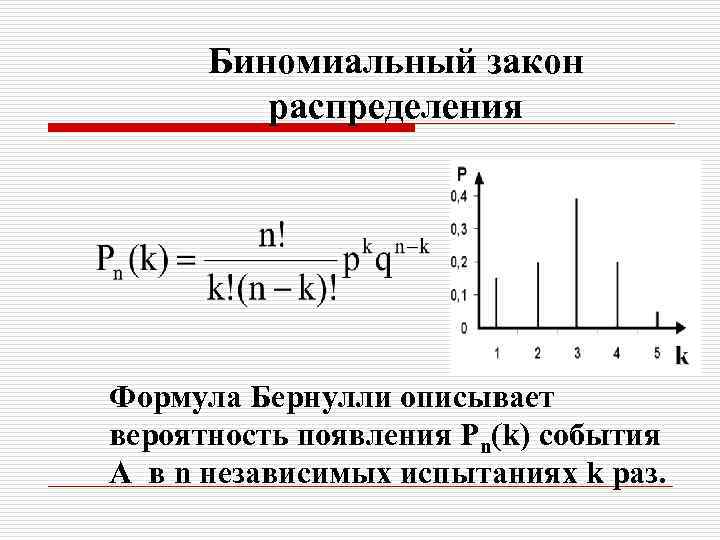
Биномиальный закон распределения Формула Бернулли описывает вероятность появления Рn(k) события А в n независимых испытаниях k раз.

Распределение Пуассона Предельный случай биномиального распределения при n , когда вероятность ожидаемого события А очень мала (p 0, а вероятность альтернативы q 1). Часто распределение Пуассона называют законом редких явлений. характеризуется средней арифметической =np и дисперсией σ2 = D причем D np

Основные характеристики непрерывных случайных величин • Функция F(х) распределения вероятностей • Функция f(x) плотности распределения вероятностей f(x)=F (x)

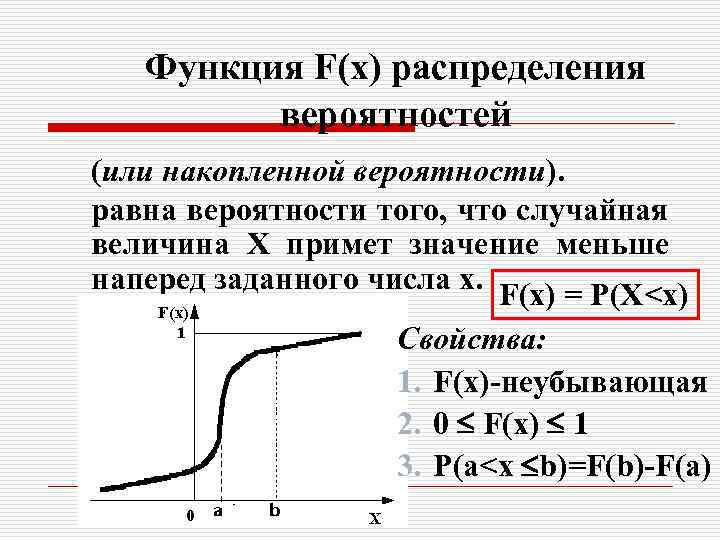
Функция F(х) распределения вероятностей (или накопленной вероятности). равна вероятности того, что случайная величина Х примет значение меньше наперед заданного числа x. F(x) = P(Х<x) Свойства: 1. F(x)-неубывающая 2. 0 F(x) 1 3. P(a<x b)=F(b)-F(a)

Плотность распределения вероятностей отношение вероятности Р(a<x<b) попадания случайной величины x в тот или иной интервал x ее значений к величине этого интервала: или при x 0:

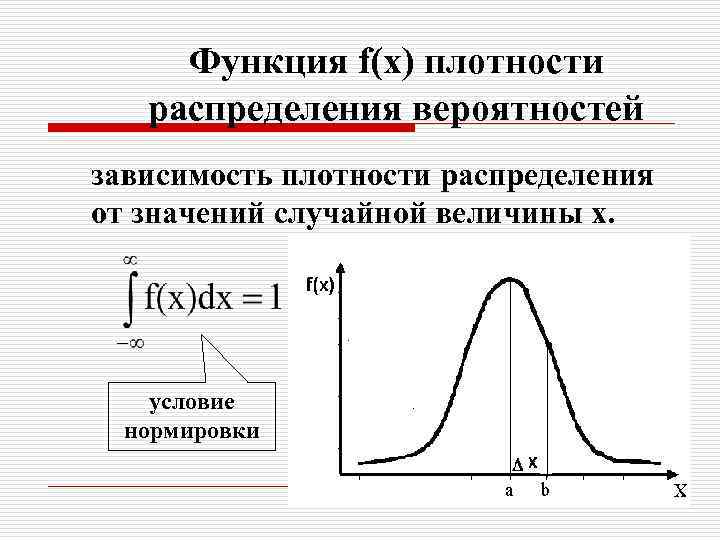
Функция f(х) плотности распределения вероятностей зависимость плотности распределения от значений случайной величины x. условие нормировки

Основные числовые характеристики непрерывных случайных величин Математическое ожидание Дисперсия Среднее квадратическое отклонение

Пример: Задана функция распределения вероятностей непрерывной случайной величины: Найти: а )функцию плотности распределения вероятностей f(Х), б) вероятность попадания случайной величины Х в интервал (0; 1). Построить графики функций F(Х) и f(Х).

Решение: Так как f(x)=F'(x), находим производные в каждом интервале:

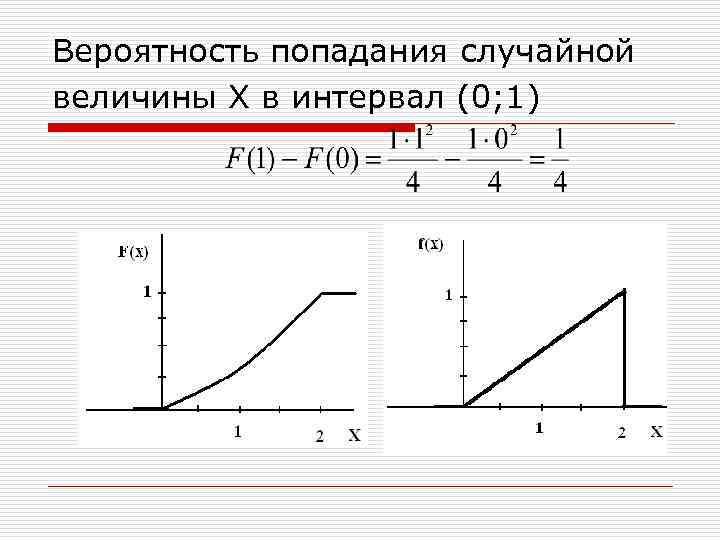
Вероятность попадания случайной величины Х в интервал (0; 1)

Распределение Максвелла распределение газовых молекул по скоростям. В равновесном состоянии макроскопические параметры газа (Р, V, Т) остаются постоянными, а микросостояния меняются. функция плотности распределения вероятности наиболее вероятная скорость молекул средняя скорость молекул

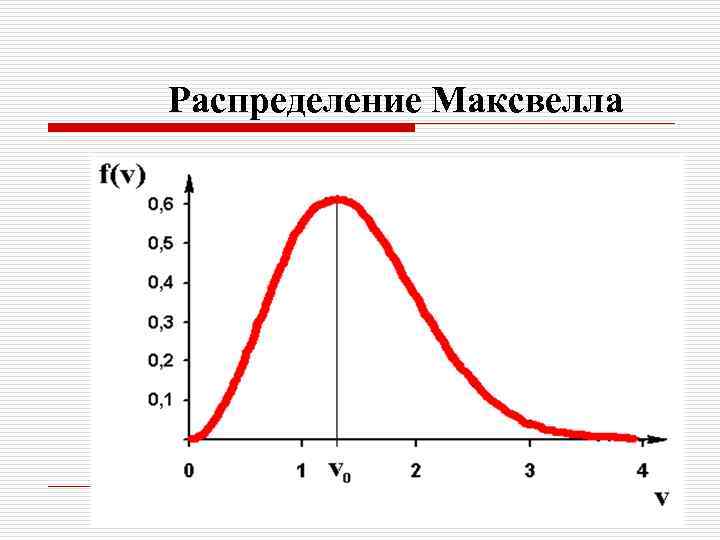
Распределение Максвелла

Распределение Больцмана распределение Больцмана – это распределение частиц в силовых полях (гравитационном, электромагнитном и т. п. ) При сравнении распределений Больцмана и Максвелла видно, что это распределения частиц по энергиям (потенциальной и кинетической)

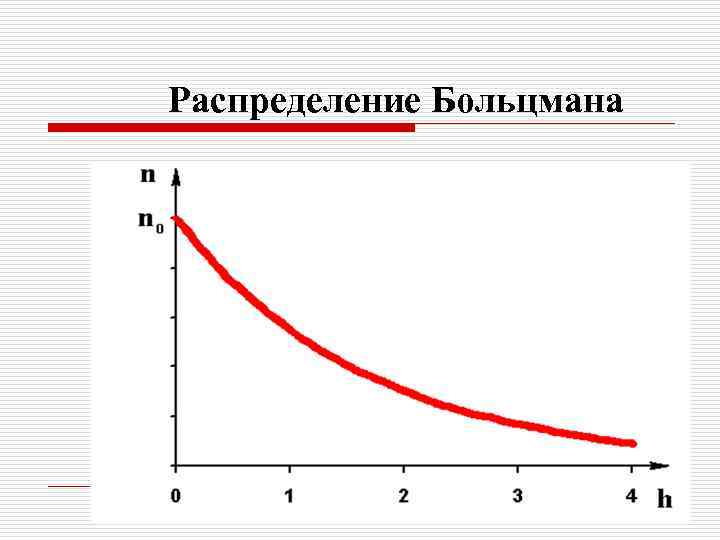
Распределение Больцмана

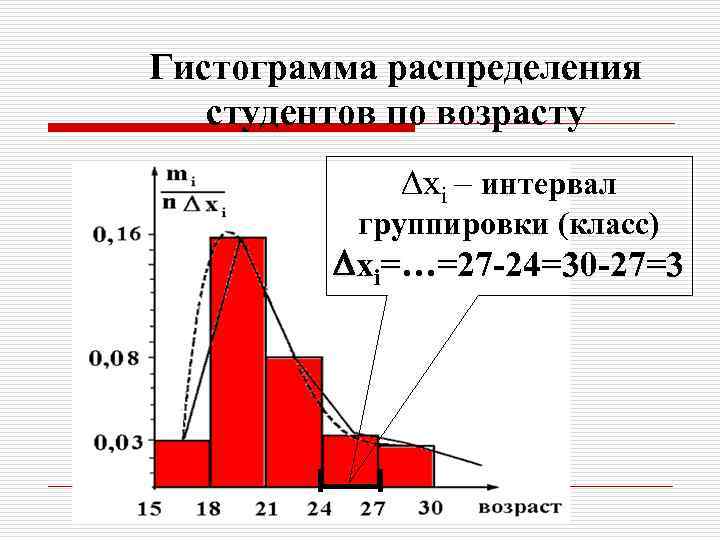
Гистограмма распределения студентов по возрасту xi – интервал группировки (класс) xi=…=27 -24=30 -27=3

Правила группировки данных 1. Из имеющихся значений признака x выбрать наименьшее (xmin), наибольшее (xmax), т. о. определяют размах распределения (xmax – xmin). 2. Определить число классов группировки: k=1+3, 32·lgn, где n – число измерений. Величину k округляют до целых чисел.

Правила группировки данных 3. Определить оптимальную величину класса (интервала группировки) 4. Выбрать границы классов. Границы первого класса следует выбрать так, чтобы он содержал наименьшее значение, но не начинался с него. Последующие классы образуются добавлением величины интервала xi. 5. Определить середину интервала <xi>.

Заключение Нами определены: o основные характеристики случайных величин (дискретных и непрерывных) и рассмотрены теоремы теории вероятностей; o Законы распределения и правила группировки данных

Тест-контроль На столе находятся 15 ампул с новокаином, 25 – с пенициллином и 10 – с лидокаином. Вероятность того, что наугад выбранная ампула окажется ампулой с пенициллином, равна: 1. 0, 1 2. 0, 15 3. 0, 25 4. 0, 5

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА Обязательная: 1. Павлушков И. В. Основы высшей математики и математической статистики: учебник для мед. вузов. - М. : ГЭОТАР-Медиа, 2007. Дополнительная: 1. Математика в примерах и задачах: учебное пособие /Л. Н. Журбенко, Г. А. Никонова, Н. В. Никонова и др. - М. : ИНФРА-М, 2010. 2. Шаповалов К. А. Основы высшей математики: учебное пособие. Красноярск: Печатные технологии, 2004 3. Математика: метод. указания к внеаудит. работе для студ. по спец. – педиатрия /сост. Л. А. Шапиро и др. - Красноярск: тип. Крас. ГМУ, 2009. Электронные ресурсы: 1. ЭБС Крас. ГМУ 2. Ресурсы интернет

Благодарю за внимание!