Кафедра фотоники и оптоинформатики. Санкт-Петербургский государственный университет информационных

Кафедра фотоники и оптоинформатики. Санкт-Петербургский государственный университет информационных технологий, механики и оптики А. В. Павлов Обработка информации оптическими методами Тема 1. 1 Отношение сигнал // помеха при корреляционном сравнении изображений. Санкт-Петербург,

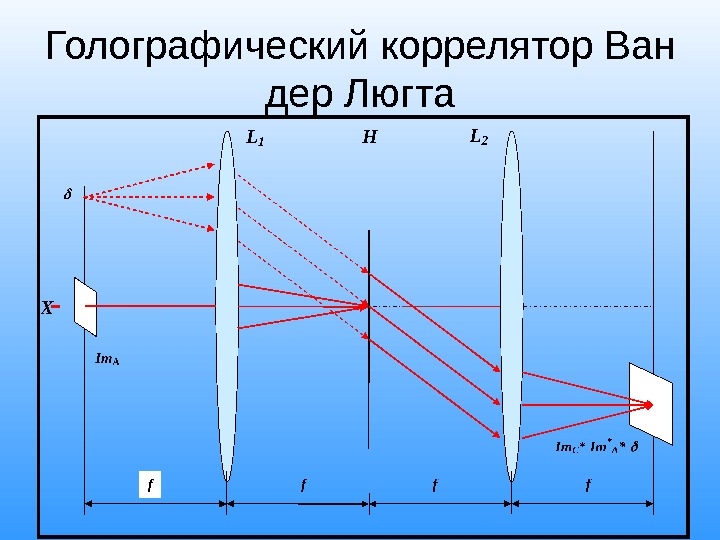
Голографический коррелятор Ван дер Люгта

Автокорреляционные функции

АКФ и ВКФ

Эталон Объектное изображение при вычислении кросс-корреляции

x y R x y. K , c x , y E x , y dxdy Опознавание осуществляется на основании вычисления функции взаимной корреляции средняя величина отношения сигнал/помеха по энергии 2 02 0 0 K , V

x y R x y K , c x , y E x , y dxdy R , c x , y dxdy S R , Математическое ожидание функции взаимной корреляции по множеству реализаций случайного поля 2 0 0 RK , R , c x , y dxdy S W максимальное значение в среднем

Средний по ансамблю квадрат помехи 2 1 1 2 2 2 1 1 2 2 2 1 1 1 2 2 2 R R R x y x y c x , y E x , y dx dy c x , y R x x , y y dx dy R , d d R E x , y RE x , y

r L

2 2 2 0 4 2 2 0 0 0 2 2 c R x y k R R , R , d d c x , y dxdy r. R r dr S S r r dr k. S r k. W S 0 1 2 R k S V k S

Строчный коррелятор 2 x c x Re ct L Кадровое окно 2 2 x c x. R L L Функция автокорреляции кадрового окна Корреляционная функция поля 2 x x. R exp r

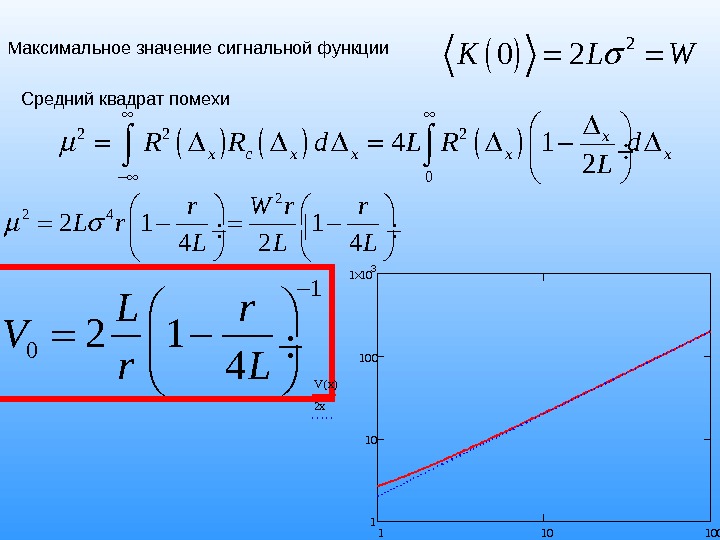
2 0 2 K L W Максимальное значение сигнальной функции Средний квадрат помехи 2 2 2 0 4 1 2 x x c x x. R R d L 2 2 4 2 1 1 4 2 4 r W r r L L L 1 0 2 1 4 L r V r L 1 10 1001101001 10 3 V x( ) 2 x x

Площадной коррелятор. Прямоугольная апертура 2 2 x y c x , y Re ct L L Максимальное значение сигнальной функци и 2 0 0 4 x y. K , L L W средний квадрат помехи 2 2 16 1 1 2 2 yx x y x y L L R , d d L L

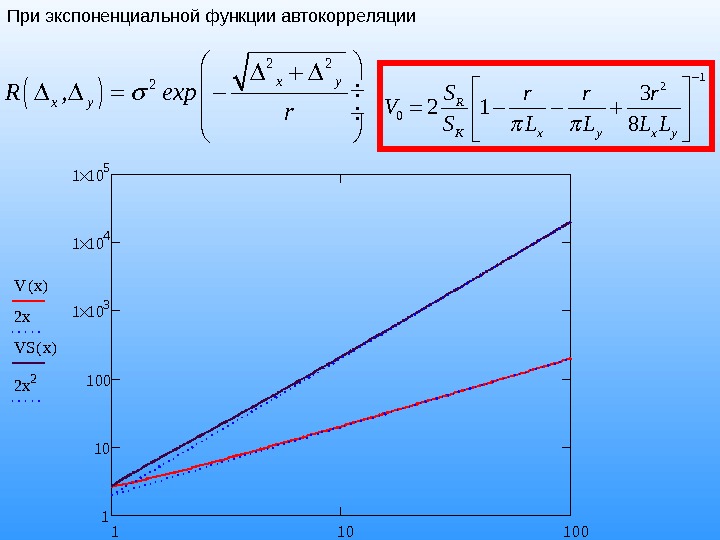
При экспоненциальной функции автокорреляции 2 2 2 x y x y. R , exp r 12 0 3 2 1 8 R K x y S r r r V S L L 1 10 1001101001 10 31 10 41 10 5 V x( ) 2 x VS x( ) 2 x