Кафедра физики ЛЕКЦИЯ 6 ПЛАН ЛЕКЦИИ 1 Модель

Кафедра физики ЛЕКЦИЯ 6 ПЛАН ЛЕКЦИИ 1. Модель атома водорода в квантовой физике. 2. Одномерное уравнение водородоподобного атома. Шредингера для 3. Квантовые числа. 4. Классификация стационарных состояний электрона в водородоподобном атоме. Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ 1

Кафедра физики КАЧЕСТВЕННАЯ МОДЕЛЬ АТОМА ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ. Нильс Бор - первая попытка построить квантовую теорию атома. Но: теория Бора имела ряд внутренних противоречий, которые ограничивали ее применение. Модель атома. В центре атома неподвижный точечный заряд (ядро), создающий вокруг себя стационарное электростатическое поле. В этом поле - отрицательный точечный заряд (электрон). Поле ядра - потенциальная яма для электрона. В связи с этим энергетический спектр электрона в поле является дискретным (квантованным). Наиболее устойчивым для электрона является состояние с минимумом энергии (основное стационарное состояние). Электрон находится в основном стационарном состоянии до тех пор, пока в поле ядра не появится какое-то сильное возмущение (например, столкновение). Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ 2

Кафедра физики КАЧЕСТВЕННАЯ МОДЕЛЬ АТОМА ВОДОРОДА В результате возмущения возбужденный уровень. электрон перескакивает на Возбужденное состояние электрона неустойчиво. Через некоторое время электрон вернется на основной уровень. Его энергия уменьшается. Освобождающуюся энергию забирает рождающийся при переходе фотон. Фотон уносит с собой порцию (квант) энергии, равную разности между возбужденным и основным уровнями энергии. Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ 3

Кафедра физики Одномерное уравнение Шредингера для водородоподобного атома. Квантование энергии Выберем систему координат, начало которой совмещено с центром атома. Это сферическая система. В такой координатной системе поле, в котором движется электрон, является центрально-симметричным. Потенциальная энергия взаимодействия электрона с ядром задается законом Кулона: Z·e – заряд ядра. Для атома водорода Z=1, для водородоподобных атомов Z > 1. Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ 4

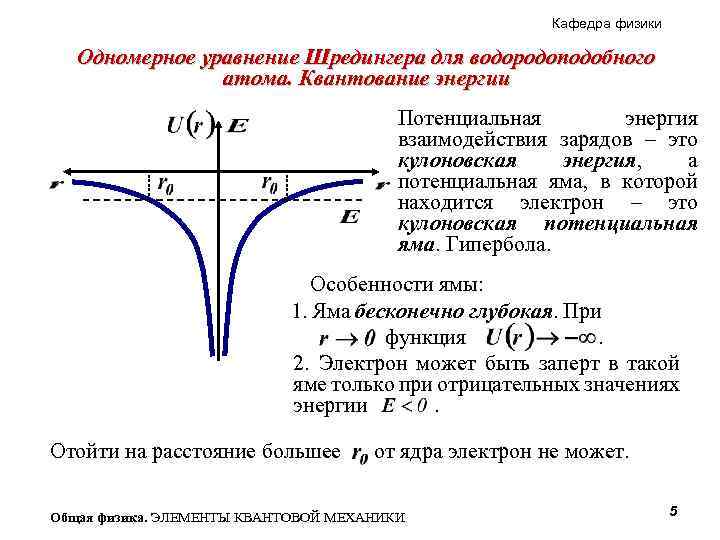Кафедра физики Одномерное уравнение Шредингера для водородоподобного атома. Квантование энергии Потенциальная энергия взаимодействия зарядов – это кулоновская энергия, а потенциальная яма, в которой находится электрон – это кулоновская потенциальная яма. Гипербола. Особенности ямы: 1. Яма бесконечно глубокая. При. функция. 2. Электрон может быть заперт в такой яме только при отрицательных значениях энергии. . Отойти на расстояние большее от ядра электрон не может. Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ 5

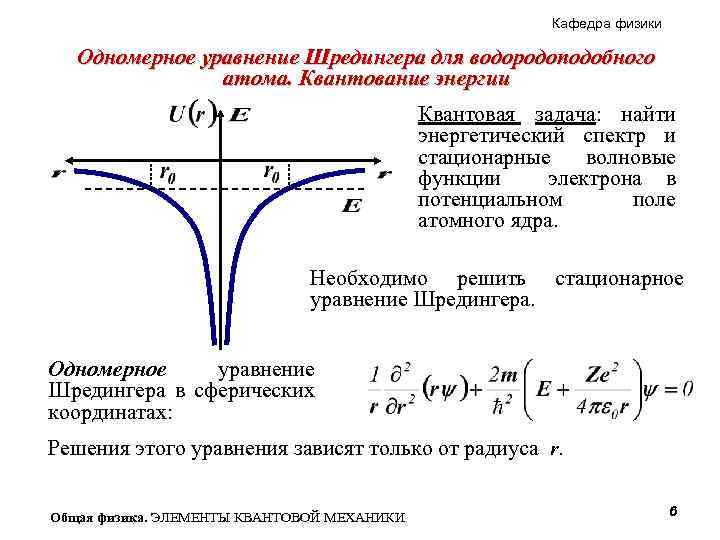Кафедра физики Одномерное уравнение Шредингера для водородоподобного атома. Квантование энергии Квантовая задача: найти энергетический спектр и стационарные волновые функции электрона в потенциальном поле атомного ядра. Необходимо решить стационарное уравнение Шредингера. Одномерное уравнение Шредингера в сферических координатах: Решения этого уравнения зависят только от радиуса r. Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ 6

Кафедра физики Одномерное уравнение Шредингера для водородоподобного атома. Квантование энергии Из теории дифференциальных уравнений: решения, удовлетворяющие условиям однозначности, конечности и непрерывности волновой функции, получаются только при собственных значениях энергии вида (n = 1, 2, 3, …), В теории Бора – то же решение. Но: Бору пришлось вводить постулаты. В квантовой механике это получается естественно из решения уравнения Шредингера. Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ 7

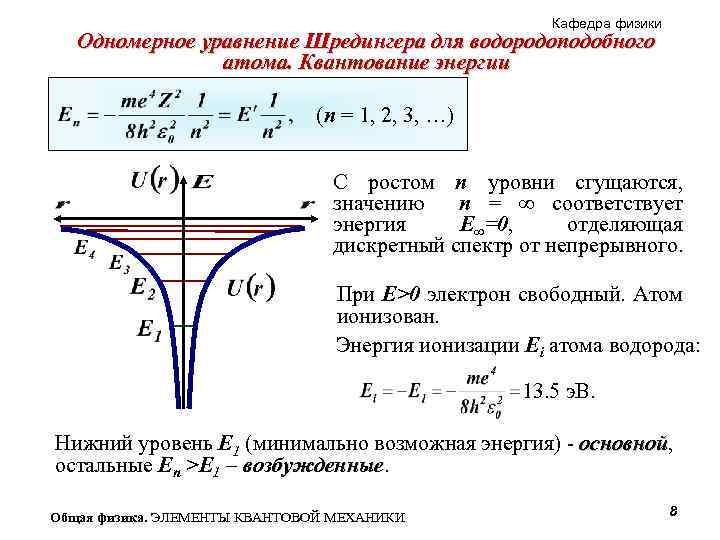Кафедра физики Одномерное уравнение Шредингера для водородоподобного атома. Квантование энергии (n = 1, 2, 3, …) С ростом n уровни сгущаются, значению n = ∞ соответствует энергия E∞=0, отделяющая дискретный спектр от непрерывного. При E>0 электрон свободный. Атом ионизован. Энергия ионизации Ei атома водорода: 13. 5 э. В. Нижний уровень E 1 (минимально возможная энергия) - основной, основной остальные En >E 1 – возбужденные Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ 8

Кафедра физики Общее решение уравнения Шредингера для водородоподобного атома. Квантовые числа. Общее решение уравнения Шредингера, зависящее от всех трех сферических координат , находят методом разделения переменных. При этом волновая функция представляется в виде произведения двух сомножителей, один из которых зависит только от r, а другой – только от углов. Но: теперь имеющие физический смысл решения уравнения Шредингера при E < 0 содержат уже не одно квантовое число n, а четыре: n, l, m, ms. Определим смысл квантовых чисел. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 9

Кафедра физики Общее решение уравнения Шредингера для водородоподобного атома. Квантовые числа. Из квантовомеханических представлений: состояние электрона в атоме водорода полностью определяется значениями четырех физических величин: - энергии E, - орбитального момента импульса L, - проекции Lz орбитального момента импульса на произвольно выбранное направление z, - проекции Lsz спинового момента импульса электрона на то же направление. Энергия. Возможные значения энергии электрона En в атоме (энергетические уровни) определяются главным квантовым числом n = 1, 2, 3, … Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 10

Кафедра физики Общее решение уравнения Шредингера для водородоподобного атома. Квантовые числа. Орбитальный (механический) момент импульса L. Всякая частица, совершающая движение по траектории (в классической механике), обладает моментом импульса Это вектор , где - радиус-вектор частицы, - ее импульс. В квантовой механике вводятся четыре параметра, связанных с моментом импульса: квадрат момента и три проекции момента импульса на координатные оси. Правило: одновременно могут иметь определенные значения лишь квадрат момента и одна из проекций момента импульса. Это означает, что вектор момента импульса не имеет определенного направления и не может изображаться, как в классической механике, отрезком прямой. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 11

Кафедра физики Общее решение уравнения Шредингера для водородоподобного атома. Квантовые числа. Из решения уравнения Шредингера: механический орбитальный момент импульса электрона квантуется, т. е. принимает только квантуется определенные дискретные значения. Эти значения определяются формулой где l – орбитальное квантовое число, которое при заданном n число принимает значения l = 0, 1, …, (n - 1). Таким образом, квантовое число l определяет момент импульса электрона в атоме. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 12

Кафедра физики Общее решение уравнения Шредингера для водородоподобного атома. Квантовые числа. Проекция Lz орбитального момента импульса на координатную ось также величина дискретная и кратная : m – магнитное квантовое число. m = 0, ± 1, ± 2, …, ±l. Видно, что магнитное квантовое число может принимать (2 l+1) значений, следовательно, столько же значений может принимать проекция Lz. Проекция Lsz спинового момента импульса электрона на направление z. Спиновый момент или спин – это параметр частицы, не зависящий от ее состояния. Иначе, это собственный механический момент импульса электрона, не связанный с его орбитальным движением. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 13

Кафедра физики Общее решение уравнения Шредингера для водородоподобного атома. Квантовые числа. Значения проекции спинового момента импульса электрона также квантованы и определяются спиновым квантовым числом ms (спиновое квантовое число часто тоже называют спином): Значения квантовых чисел n, l, m, ms полностью определяют квантовомеханическое состояние электрона в атоме водорода. Квантовые числа n, l, m появляются при решении нерелятивистского уравнения Шредингера, а спиновое квантовое число ms появляется лишь при решении уравнения Дирака, (релятивистское уравнение Шредингера). Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 14

Кафедра физики Классификация стационарных состояний электрона в водородоподобном атоме. Энергия электрона En в атоме зависит только от n, поэтому одной энергии (одному энергетическому уровню) соответствует несколько электронных состояний, отличающихся значениями l, m. Следовательно, можно дополнить квантовую модель атома водорода. Электрон при своем движении как бы размазан по всему объему, образуя электронное облако, плотность которого характеризует вероятность обнаружения электрона в единице объема. Квантовые числа n и l определяют размер и форму электронного облака, а квантовое число m характеризует ориентацию электронного облака в пространстве. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 15

Кафедра физики Классификация стационарных состояний электрона в водородоподобном атоме. Вывод: энергетическому уровню может соответствовать несколько квантовых состояний. Эти состояния необходимо обозначать. Используется система обозначения состояний электрона, заимствованная из спектроскопии. Состояния с различными значениями орбитального квантового числа l обозначают различными латинскими буквами: l = 0 – буквой s (s - состояние); l = 1 – буквой p (p - состояние); l = 2 – буквой d (d - состояние). Далее идут f, g, h – состояния и т. д. по алфавиту. Значение главного квантового числа указывается перед условным обозначением квантового числа l. Пример: электрон в состоянии с n = 3 и l = 1 обозначается как 3 p. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 16