Кафедра физики ЛЕКЦИЯ 5 ПЛАН ЛЕКЦИИ 1 Квантовый

Кафедра физики ЛЕКЦИЯ 5 ПЛАН ЛЕКЦИИ 1. Квантовый ротатор 2. Атом водорода. Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ 1

Кафедра физики КВАНТОВАНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ Аналогия: Ĺz – оператор проекции момента импульса на ось z. Ψ-функция может зависеть не только от (x, y, z), но от любой координаты, например угла φ. Аналогия: При повороте на 2π любой объект возвращается в прежнее состояние. Следовательно: Момент импульса квантуется! 2

Кафедра физики Уравнение Шредингера для водородоподобного атома. Квантование энергии Выберем систему координат, начало которой совмещено с центром атома. В такой координатной системе поле, в котором движется электрон, является центрально-симметричным. Потенциальная энергия взаимодействия электрона с ядром задается выражением: Z·e – это заряд ядра. Для атома водорода, ядро которого состоит из одного протона, Z=1, для водородоподобных атомов Z > 1. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 3

Кафедра физики Уравнение Шредингера для водородоподобного атома. Квантование энергии Водородоподобными называют атомы (ионы) с одним электроном и ядром, содержащим несколько протонов. Примеры: ионы гелия , лития и другие. Потенциальная энергия взаимодействия зарядов – это кулоновская энергия, а потенциальная яма, в которой находится электрон – это кулоновская потенциальная яма. Кулоновская потенциальная яма имеет форму гиперболы. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 4

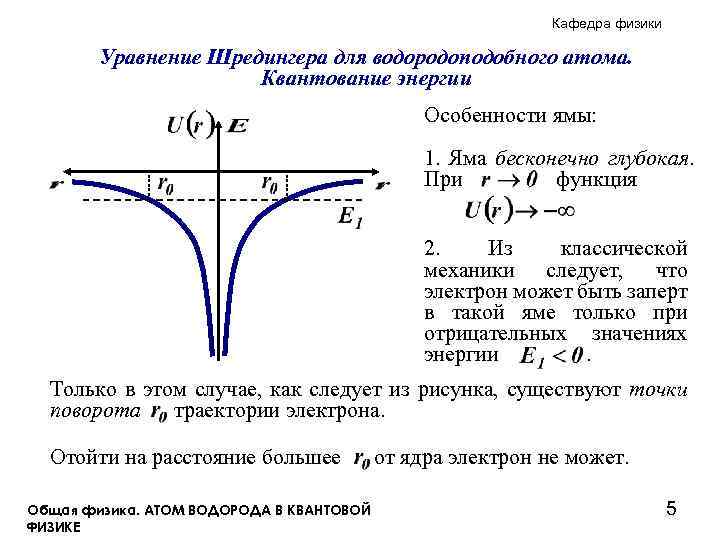Кафедра физики Уравнение Шредингера для водородоподобного атома. Квантование энергии Особенности ямы: 1. Яма бесконечно глубокая. При функция 2. Из классической механики следует, что электрон может быть заперт в такой яме только при отрицательных значениях энергии. Только в этом случае, как следует из рисунка, существуют точки поворота траектории электрона. Отойти на расстояние большее Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ от ядра электрон не может. 5

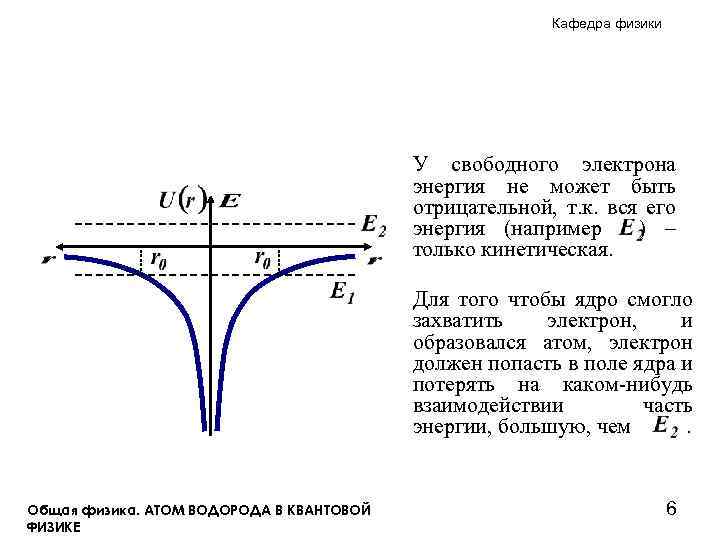Кафедра физики У свободного электрона энергия не может быть отрицательной, т. к. вся его энергия (например ) – только кинетическая. Для того чтобы ядро смогло захватить электрон, и образовался атом, электрон должен попасть в поле ядра и потерять на каком-нибудь взаимодействии часть энергии, большую, чем. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 6

Кафедра физики Рассмотрим водородоподобный атом с позиций квантовой механики. В рамках квантовой механики задача состоит в нахождении стационарных волновых функций и энергетического спектра электрона в потенциальном поле атомного ядра. Для этого необходимо решить стационарное уравнение Шредингера: z x r y Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ Поскольку потенциальная энергия зависит только от r, это уравнение следует решать в сферической системе координат с центром на ядре. 7

Кафедра физики С помощью формул преобразования оператор Лапласа в уравнении Шредингера можно записать в сферической системе координат. Решение уравнения Шредингера ищется в виде произведения двух функций: Уравнение Шредингера распадается на два уравнения. Одно по r, другое по θ, φ. При решении первого уравнения возникает квантовое число n, которое определяет полную энергию электрона. Решение второго уравнения приводит к появлению еще двух чисел l и m. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 8

Кафедра физики Квантование энергии Первое уравнение имеет решения при значениях полной энергии, определяемых формулой: (n = 1, 2, 3, …), т. е. при дискретном наборе отрицательных значений энергии. Квантовая механика приводит к таким же значениям энергии водородоподобного атома, что и теория Бора (см. лекцию 3). Но: Бору для получения такого результата пришлось вводить специальные предположения (постулаты). В квантовой механике это получается естественно из решения уравнения Шредингера. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 9

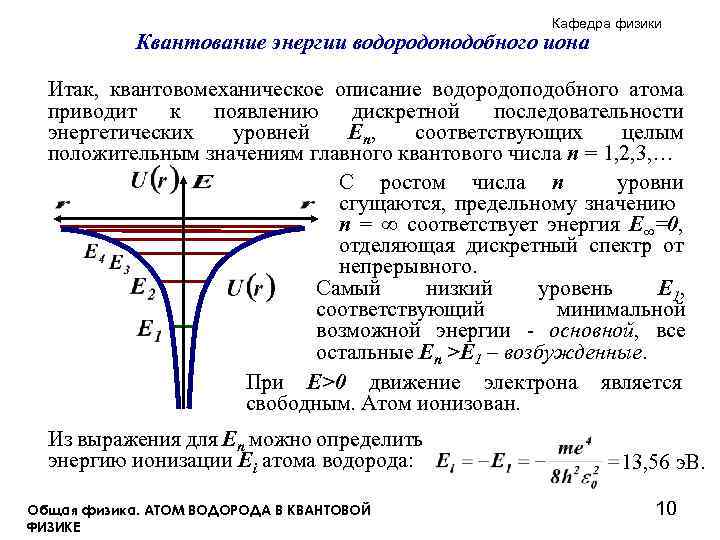Кафедра физики Квантование энергии водородоподобного иона Итак, квантовомеханическое описание водородоподобного атома приводит к появлению дискретной последовательности энергетических уровней E n, соответствующих целым положительным значениям главного квантового числа n = 1, 2, 3, … С ростом числа n уровни сгущаются, предельному значению n = ∞ соответствует энергия E∞=0, отделяющая дискретный спектр от непрерывного. Самый низкий уровень E 1, соответствующий минимальной возможной энергии - основной, все остальные En >E 1 – возбужденные. При E>0 движение электрона является свободным. Атом ионизован. Из выражения для En можно определить энергию ионизации Ei атома водорода: Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 13, 56 э. В. 10

Кафедра физики Общее решение уравнения Шредингера для водородоподобного атома. Квантовые числа. Общее решение уравнения Шредингера, зависящее от всех трех сферических координат , может быть найдено методом разделения переменных. В соответствии с этим методом волновая функция. представляется в виде произведения двух сомножителей, один из которых зависит только от а другой – только от углов. При этом оказывается, что имеющие физический смысл решения уравнения Шредингера при E<0 содержат уже не одно квантовое число n, а три квантовых числа n, l, m. Определим смысл квантовых чисел. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 11

Кафедра физики Общее решение уравнения Шредингера для водородоподобного атома. Квантовые числа. Из квантовомеханических представлений: состояние электрона в атоме водорода полностью определяется значениями трех физических величин: - энергии E, - орбитального момента импульса L, - проекции Lz орбитального момента импульса на произвольно выбранное направление z, Энергия. Возможные значения энергии электрона En в атоме (энергетические уровни) определяются главным квантовым числом n, принимающим целочисленные значения, начиная с единицы: n = 1, 2, 3, … (n = 1, 2, 3, …), Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 12

Кафедра физики Орбитальный (механический) момент импульса L. Всякая частица, совершающая движение по траектории, обладает моментом импульса. Это вектор, который по определению равен , где - радиус -вектор частицы, - ее импульс. В квантовой механике вводятся четыре оператора, касающихся момента импульса: оператор квадрата момента и три оператора проекций момента импульса на координатные оси: Для того, чтобы определить, обладает ли частица в данном состоянии определенными значениями какой-либо величины, нужно решить уравнение квантования: - Оператор, Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ А - величина. 13

Кафедра физики Применим это правило к оператору проекции момента импульса Решим уравнение квантования: Что это означает? Это означает, что в состоянии, описываемом функцией Ψ, Электрон обладает определенным значением Lz Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 14

Кафедра физики Общее решение уравнения Шредингера для водородоподобного атома. Квантовые числа. Применение этого правила для найденной ψ-функции, т. е. решение уравнения: Приводит к результату: или где l – орбитальное квантовое число, которое при заданном n принимает значения l = 0, 1, …, (n - 1). Таким образом, квантовое число l определяет модуль момента импульса электрона в атоме. Этот момент – орбитальный. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 15

Кафедра физики Решение уравнения Дает: m –магнитное квантовое число, которое при заданном l принимать значения m = 0, ± 1, ± 2, …, ±l. может Проекция Lz орбитального момента импульса на координатную ось также величина дискретная и кратная. Магнитное квантовое число может принимать (2 l+1) значений, следовательно, столько же значений может принимать проекция Lz орбитального момента импульса на ось координат. Орбитальное движение электрона означает существование кругового тока, а следовательно, магнитного момента μ гиромагнитное отношение. магнетон Бора. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 16

Кафедра физики Найдем гиромагнитное отношение по модели Бора: Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 17

Спин Кафедра физики Эксперименты, проведенные в 1925 году студентами Геттингенского университета (Голландия) Гаудсмитом и Уленбеком, натолкнули их на мысль о существовании у электрона собственного механического момента, подобного тому, который есть у вращающегося тела. s=1/2 – спиновое квантовое число. Проекция Lsz спинового момента импульса электрона на направление z: Формулы квантования похожи на те, которые использованы для орбитального момента. У электрона есть и собственный магнитный момент: Проекция на ось z равна: 18

Кафедра физики Возможные значения проекции спинового момента импульса электрона также квантованы и определяются спиновым квантовым числом ms (спиновое квантовое число часто тоже называют спином): Значения квантовых чисел n, l, m, ms полностью определяют квантовомеханическое состояние связанного электрона в атоме водорода. Квантовые числа n, l, m появляются при решении нерелятивистского уравнения Шредингера, а спиновое квантовое число ms появляется лишь при решении уравнения Дирака, (релятивистское обобщение уравнения Шредингера). Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 19

Кафедра физики Классификация стационарных состояний электрона в водородоподобном атоме. Энергия электрона En в атоме зависит только от главного квантового числа n, поэтому одному энергетическому уровню с заданным значением n соответствует несколько различных электронных состояний, отличающихся значениями l, m. Энергетический уровень, которому соответствует только одно квантовое состояние, называется невырожденным, а если уровню соответствует несколько квантовых состояний, то он называется вырожденным. Число различных состояний , соответствующих определенному энергетическому уровню, называется кратностью вырождения этого уровня. Вычислим кратность вырождения энергетического уровня En с заданным значением n. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 20

Кафедра физики Классификация стационарных состояний электрона в водородоподобном атоме. Орбитальное квантовое число l может изменяться от 0 до (n – 1). При этом каждому значению l соответствует 2 l+1 различных значений m. Тогда общее число различных состояний при заданном значении n можно определить суммированием по возможным значениям l: без учета спина. Если учесть еще одно квантовое число - спин частицы, то кратность вырождения уровня с заданным n увеличится в два раза (спиновое квантовое число ms принимает два значения): Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 21

Кафедра физики Классификация стационарных состояний электрона в водородоподобном атоме. n 1 l 0 0 2 1 0 3 1 2 m 0 0 0 -1 +1 0 -1 -2 +1 +2 ms ± 1/2 ± 1/2 ± 1/2 ± 1/2 22

Кафедра физики Классификация стационарных состояний электрона в водородоподобном атоме. Дополнительные квантовые числа получаются из решения уравнений Шредингера с учетом ограничительных условий, налагаемых на волновую функцию. Из квантовой механики: каждому энергетическому состоянию электрона в атоме соответствует своя волновая функция, квадрат модуля которой определяет вероятность обнаружения электрона в единице объема. Электрон при своем движении как бы размазан по всему объему, образуя электронное облако, плотность которого характеризует вероятность обнаружения электрона в единице объема. Квантовые числа n и l определяют размер и форму электронного облака, а квантовое число m характеризует ориентацию электронного облака в пространстве. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 23

Кафедра физики Классификация стационарных состояний электрона в водородоподобном атоме. Каждому энергетическому уровню может соответствовать несколько квантовых состояний. Следовательно, эти состояния необходимо каким-то образом обозначать. В атомной физике используется система условных обозначений состояний электрона, заимствованная из спектроскопии. Состояния с различными значениями азимутального квантового числа l различаются значениями момента импульса: s (l=0), p (l=1) Далее идут d, f, g, h – состояния и т. д. по алфавиту. Значение главного квантового числа указывается перед условным обозначением квантового числа l. Пример: электрон в состоянии с n=3 и l=1 обозначается символом 3 p. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 24

Кафедра физики СПЕКТР АТОМА ВОДОРОДА. Спектры излучения электромагнитных волн водородоподобных атомов являются простейшими. Их простота физически связана с наличием в атомах только одного электрона, а математически с тем, что положение энергетических уровней зависит лишь от одного квантового числа n. Многоэлектронные атомы имеют значительно более сложные спектры. Спектр атома водорода состоит из отдельных тонких спектральных линий (линейчатый спектр), положение которых на шкале частот однозначно связано с положением соответствующих энергетических уровней в энергетическом спектре атома. Изобразим схему энергетических уровней атома водорода. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 25

Кафедра физики СПЕКТР АТОМА ВОДОРОДА. Покажем условно на схеме квантовые состояния некоторых вырожденных уровней. Для этого обратимся к квалификации стационарных состояний электрона в атоме водорода и запишем возможные его состояния, например, для четырех первых уровней. Исходя из возможных значений квантовых чисел l и полагая для простоты m=0, запишем возможные состояния электрона: 1 s – электрон находится в состоянии с n = 1 и l = n - 1 = 0. Это s – состояние; 2 s, 2 p – при n = 2 возможны два состояния с l = 0 и l = 1 (соответственно s- и p - состояния); 3 s, 3 p, 3 d – к предыдущим добавляется еще одно возможное состояние с l = 2 - d - состояние; 4 s, 4 p, 4 d, 4 f – добавляется еще одно возможное состояние с l=3 - f – состояние. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 26

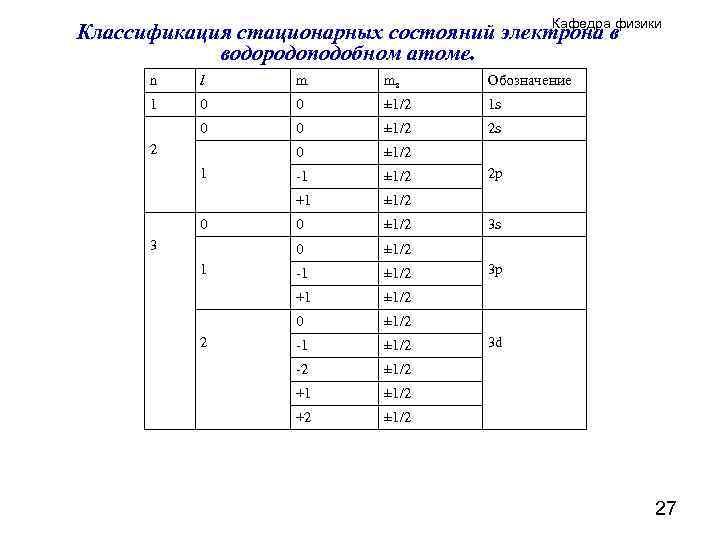Кафедра физики Классификация стационарных состояний электрона в водородоподобном атоме. n l m ms Обозначение 1 0 0 ± 1/2 1 s 0 0 ± 1/2 2 s 0 ± 1/2 -1 ± 1/2 +1 ± 1/2 0 ± 1/2 -1 ± 1/2 -2 ± 1/2 +1 ± 1/2 +2 ± 1/2 2 1 0 3 1 2 2 p 3 s 3 p 3 d 27

Кафедра физики СПЕКТР АТОМА ВОДОРОДА. Вспомним формулу для энергии квантовых состояний электрона (лекции 3, 8): (n = 1, 2, 3, …). После подстановки соответствующих значений величин эту формулу можно представить в виде: постоянных (n = 1, 2, 3, …). С помощью этой формулы рассчитаем энергетические уровни атома водорода. Изобразим некоторые квантовые состояния атома. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ 28

0 -2 -4 n 5 4 3 s l=0 p l=1 d l=2 f l=3 g l=4 2 -6 -8 5 s, 5 p, 5 d, 5 f, 5 g 4 s, 4 p, 4 d, 4 f Кафедра физики СПЕКТР АТОМА ВОДОРОДА. Состояние атома 1 s , в котором электрон находится на нижнем энергетическом уровне En = – 13, 6 э. В, называется основным или нормальным и является стационарным. 3 s, 3 p, 3 d -10 2 s, 2 p -12 1 s -13, 6 1 Энергия, э. В Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ Атом, не подверженный внешнему воздействию, может находиться в основном состоянии неопределенно долго. 29

0 -2 -4 n 5 4 3 s l=0 2 p l=1 d l=2 f l=3 g l=4 Кафедра физики СПЕКТР АТОМА ВОДОРОДА. Энергетический уровень E 1 бесконечно тонким. является Это вытекает из соотношения неопределенностей. -6 -8 -10 Неопределенность полной энергии микрочастицы E в некотором квантовом состоянии связана с неопределенностью времени ее пребывания в этом состоянии соотношением, которое для уровня E 1 можно записать в виде: -12 -13, 6 1 Энергия, э. В Поскольку Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ , то . 30