Кафедра ЕФЭ Презентация по курсам Общая физика и

Кафедра ЕФЭ Презентация по курсам «Общая физика» и «Физика I, II» (постоянный ток) Доц. Курбачев Ю. Ф.

4. 1. Сила тока I есть физическая величина, численно равная заряду, прошедшему через поперечное сечение проводника за единицу времени. Если через поперечное сечение проводника прохо дят заряд Δ за q время, то Δt сила тока равна. (4. 1) 4. 2. Вектор плотности тока (4. 2) где Δq – заряд, прошедший через площадку за время Δt, j– плотность тока.

(4. 3) (4. 4) Отсюда Рис. 4. 1 тогда Из рис 4. 1 видно, что , где проекция j на нормаль к площадке ΔS, откуда имеем: (2. 4) (4. 5)

Из равенства 4. 5 можно определять силу тока через всю площадь сечения проводника (4. 6) 4. 3. Закон Ома для однородного участка цепи. Сопротивление проводников. I=f(U) I=k. U (4. 7) Обозначим сопротивление через R, тогда или (4. 8)

(4. 9) (4. 10) где ρ удельное сопротивление проводника; l длина проводника; S - площадь его поперечного сечения. (4. 11) 4. 4. Закон Ома в дифференциальной форме

Рис. 4. 2 (4. 12) где сопротивление этого участка. Подставляя в равенство (4. 12) последнее равенство, имеем (4. 13) Но так как и или в векторном виде , имеем j=σE (4. 14) (4. 15)

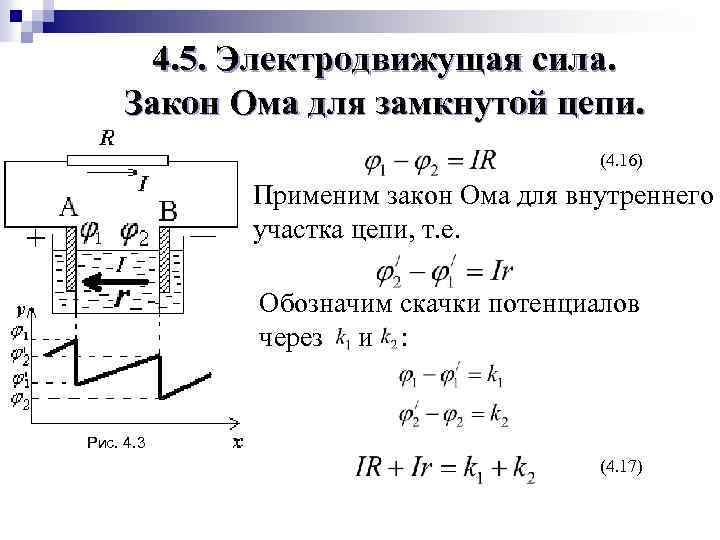
4. 5. Электродвижущая сила. Закон Ома для замкнутой цепи. (4. 16) Применим закон Ома для внутреннего участка цепи, т. е. Обозначим скачки потенциалов через и : Рис. 4. 3 (4. 17)

(4. 18) тогда имеем (4. 19) или (4. 20) Это и есть закон Ома для замкнутой цепи. Заметив, что , получим из формулы (4. 19): (4. 21) Если I=0, т. е. цепь разомкнута, то (4. 22) а это значит, что электродвижущая сила есть величина, численно равная разности потенциалов на зажимах разомкнутого элемента.

(4. 23) (4. 24) Если q=+1, то ε=A, т. е. ЭДС источника есть величина, численно равная работе, совершаемой при перемещении единицы заряда по замкнутой цепи. (4. 25) 4. 6. Закон Ома для неоднородного участка цепи Рис. 4. 4

В местах контактов образуется разность потенциалов: (4. 26) Для каждого проводника в отдельности применим закон Ома: где RA, RB, RC и RD сопротивления проводников соответственно A, B, C и D.

Складывая последние равенства, найдем: (4. 27) (4. 28) Здесь где ε ЭДС, действующая на данном неоднородном участке. Полное сопротивление участка R: (4. 29) R=RA+RB+RC+RD или (4. 30) Это и есть закон Ома для неоднородного участка цепи.

Этот закон является наиболее общим законом Ома, и из него легко получить два других. Для однородного , тогда участка цепи , тогда Для замкнутой цепи. 4. 7. Мощность, выделяемая в цепи. , то Но так как по закону Ома для замкнутой цепи (4. 31)

Т. к. по закону Ома то полную мощность можно выразить через внешнее сопротивление, исходя из формулы(4. 31) (4. 32) Полная мощность имеет наибольшее значение при токе короткого замыкания, т. е. при R=0: Рис. 4. 5

Мощность, выделенная на внешнем участке цепи, Pa равна: (4. 33) R=r (4. 34) Коэффициент полезного действия источника η есть величина, численно равная отношению мощности, выделенной на внешнем участке цепи, к полной мощности: (4. 35)

4. 8. Закон Джоуля-Ленца. Интегральная форма закона. (4. 36) (4. 37) (4. 38) Если I изменяется со временем, то (4. 39)

4. 9. Закон Джоуля-Ленца в дифференциальной форме. Плотность тепловой мощности: (4. 40) Но так как и , то, подставляя последние два равенства в формулу (4. 40), получим: (4. 41) где плотность тока. (4. 42) (4. 43)

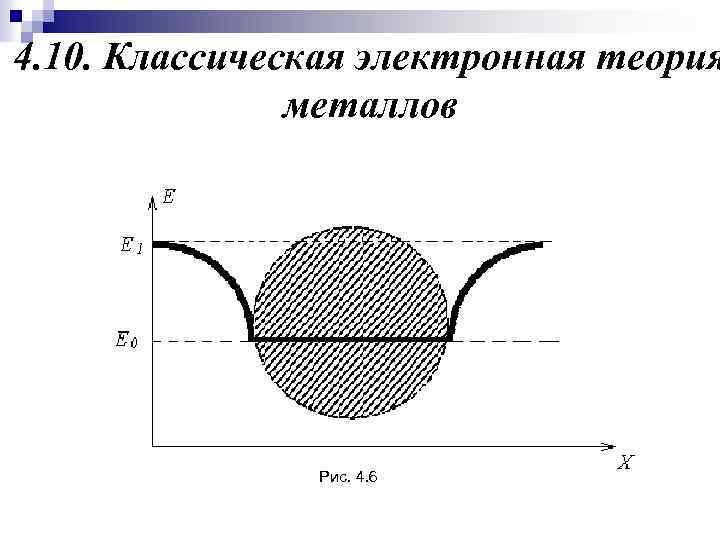
4. 10. Классическая электронная теория металлов Рис. 4. 6

4. 11. Закон Ома с точки зрения классической электронной теории Как мы уже знаем плотность тока (4. 44) где q переносимый заряд; S площадь поперечного сечения проводника; t время переноса заряда. Переносимый заряд равен: (4. 45) где e заряд электрона; n 0 число электронов в единице объема.

Подставляя формулу (4. 45) в (4. 44), получим (4. 46) (4. 47) Между столкновениями электрон движется равноускоренно, т. к. E=const, тогда (4. 48) где a ускорение электрона; t время между двумя столкновениями. По второму закону Ньютона: (4. 49) Здесь m масса электрона.

(4. 50) где - средняя скорость беспорядочного теплового движения, т. к. при обычных плотностях тока Подставляя формулу (4. 49) и (4. 50) в (4. 48), а (4. 48) в (4. 47), получим окончательное выражение для средней скорости направленного движения (4. 51) (4. 52) (4. 53) (4. 54)

Подсчитаем количество теплоты, выделенное в единице объема проводника за единицу времени. (4. 55) К концу свободного пробега электрон приобретает скорость , как было показано выше, равную (4. 56) Следовательно, кинетическая энергия, которую электрон передаст решетке при одном столкновении, будет: (4. 57) За единицу времени электрон столкнется Z раз. Число столкновений:

Плотность тепловой мощности: (4. 58) где , окончательно имеем: , что является законом Джоуля Ленца. (4. 59)