КАЧЕСТВЕННАЯ ОЦЕНКА РЕЗУЛЬТАТОВ ДА НЕТ Пример 1 Пример

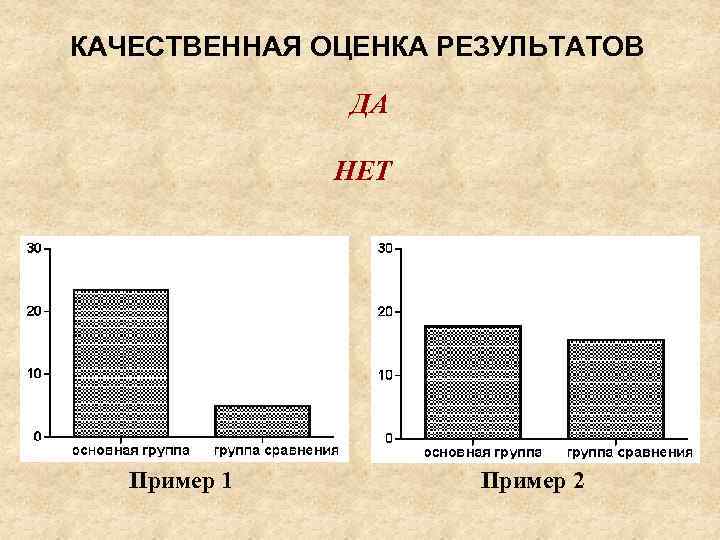КАЧЕСТВЕННАЯ ОЦЕНКА РЕЗУЛЬТАТОВ ДА НЕТ Пример 1 Пример 2

Критерий χ2 - критерий Пирсона Критерий χ2 применяется в двух целях: 1. для сопоставления эмпирического распределения признака с теоретическим - равномерным, нормальным или каким-то иным; 2. для сопоставления двух, трех или более эмпирических распределений одного и того же признака. Критерий χ2 отвечает на вопрос о том, с одинаковой ли частотой встречаются разные значения признака в эмпирическом и теоретическом распределениях или в двух и более эмпирических распределениях. Автоматический расчет: http: //www. psychol-ok. ru/statistics/pearson/

ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ КРИТЕРИЕЯ χ2 Вычисление критерия Хи-квадрат для таблиц сопряженности 2 х2 Данный анализ позволит ответить на вопрос «Можно ли утверждать, исходя из данных выборки, что два исследуемых дискретных, качественных признака независимы друг от друга в генеральной совокупности? » Иными словами, что между этими признаками отсутствует взаимосвязь. Если эта гипотеза будет отвергнута, то с большой долей вероятности мы можем утверждать, что такая зависимость существует.

РАСЧЕТ КРИТЕРИЕЯ χ2 Признак А Наличие A Отсутствие A Всего Признак В Наличие B a c a+c Отсутствие B b d b+d Всего a+b c+d N=a+b+c+d

ПРИМЕР РАСЧЕТА КРИТЕРИЕЯ χ2 Пример. У 33 матерей принимавших таблетки дети болели желтухой, а у 24 матерей также принимавших таблетки дети не болели желтухой. Далее, у 14 матерей которые не принимали таблетки, дети болели желтухой и у 45 матерей не принимавших таблетки, дети не болели желтухой. Наличие заболевания у детей Прием матерью таблеток Есть желтуха Нет желтухи Всего Принимала таблетки 33 24 57 Не принимала таблетки 14 45 59 Всего 47 69 116

ПРИМЕР РАСЧЕТА КРИТЕРИЕЯ χ2 Объем выборки для данного примера равен 116. Обозначим градации по строкам как A 1 (прием таблеток) и A 2 (таблетки не принимались), а градации по столбцам обозначим как B 1 (дети больны желтухой) и B 2 (желтухи нет). Соответствующие комбинации этих градаций между собой будем обозначать как A 1 B 1 (33), A 1 B 2 (24), A 2 B 1 (14) и A 2 B 2 (45). χ2 = 14, 042 Уровни значимости "р" Критические значения p = 0, 000179 p < 0, 005 0, 025 0, 01 0, 005 3, 842 5, 024 6, 635 7, 880

ОГРАНИЧЕНИЯ КРИТЕРИЕЯ χ2 Ожидаемые частоты, которые вычисляются исходя из гипотезы независимости признаков, должны иметь значения не менее 5. Если эти частоты имеют значения менее 5, то появляется соответствующее предупреждение. Оно означает, что ваш результат неустойчив и имеет смысл увеличить объем выборки. В том случае, когда нулевая гипотеза о независимости признаков отвергается (вычисленное значение статистики хи-квадрат больше критического), необходим дальнейший анализ этой таблицы. Такой детальный анализ таблицы сопряженности, особенно для таблиц с числом градаций более двух - 3 х3, 3 х4, 4 х5 и т. д. может провести только опытный биостатистик. Отметим, что результаты такого анализа могут дать очень много полезной информации.

ПОПРАВКА ЙЕТСА ДЛЯ КРИТЕРИЕЯ χ2 Поправка на «непрерывность» связана с тем, что непрерывные распределения хи-квадрат и соответственно нормальное распределение, используются для представления дискретных выборочных частот. С учетом такой поправки данное выражение примет следующий вид: http: //www. biometrica. tomsk. ru/freq 2. htm

ЛИТЕРАТУРА http: //www. machinelearning. ru/wiki/index. php? title=%D 0%9 C%D 0%BE%D 1% 89%D 0%BD%D 0%BE%D 1%81%D 1%82%D 1%8 C_%D 0%BA%D 1%80%D 0% B 8%D 1%82%D 0%B 5%D 1%80%D 0%B 8%D 1%8 F#. D 0. A 1. D 0. B 2. D 0. BE. D 0. B 9. D 1. 81. D 1. 82. D 0. B 0_. D 1. 81. D 1. 82. D 0. B 0. D 1. 82. D 0. B 8. D 1. 81. D 1. 82. D 0. B 8. D 1. 87. D 0. B 5. D 1. 81. D 0. BA. D 0. B 8. D 1. 85_. D 0. BA. D 1. 80. D 0. B 8. D 1. 82. D 0. B 5. D 1. 80. D 0. B 8. D 0. B 5. D 0. B 2 http: //www. biometrica. tomsk. ru/freq 1. htm http: //www. matlab. mgppu. ru/work/0022. htm http: //dic. academic. ru/dic. nsf/ruwiki/989265 http: //www. biometrica. tomsk. ru/freq 2. htm

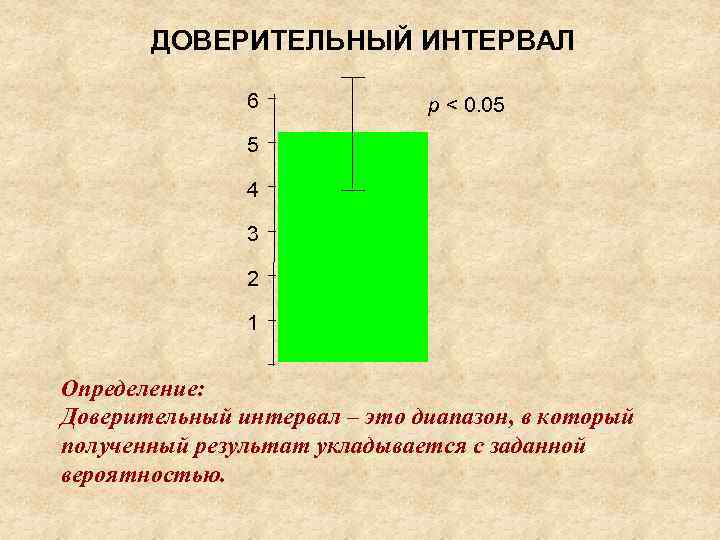ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ 6 p < 0. 05 5 4 3 2 1 Определение: Доверительный интервал – это диапазон, в который полученный результат укладывается с заданной вероятностью.

ВЫЧИСЛЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА р – частота ожидаемого события q – частота противоположного события n – полное число событий в группе Условие применения: np > 5, nq > 5