К. Ю. Поляков Множества и логика в задачах ЕГЭ по информатике Множества и логика в задачах ЕГЭ // Информатика, № 10, 2015, с. 38 -42. К. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
2 Множества и логика в задачах ЕГЭ по информатике Постановка задачи На числовой прямой даны два отрезка: P = [37; 60] и Q = [40; 77]. Укажите наименьшую возможную длину такого отрезка A, что выражение (x P) → (((x Q) ¬(x A)) → ¬(x P)) истинно при любом значении переменной х. Элементами множеств А, P и Q являются натуральные числа, причём P = {2, 4, 6, 8, 10, 12} и Q = {4, 8, 12, 116}. Известно, что выражение (x P) → (((x Q) ¬(x A)) → ¬(x P)) истинно при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A. ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
3 Множества и логика в задачах ЕГЭ по информатике Постановка задачи Для какого наибольшего натурального числа А выражение ¬ДЕЛ(x, А) (ДЕЛ(x, 6) ¬ДЕЛ(x, 4)) тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной х)? Определите наименьшее натуральное число A, такое что выражение (x & 53 0) ((x & 41 = 0) (x & A 0)) тождественно истинно? ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
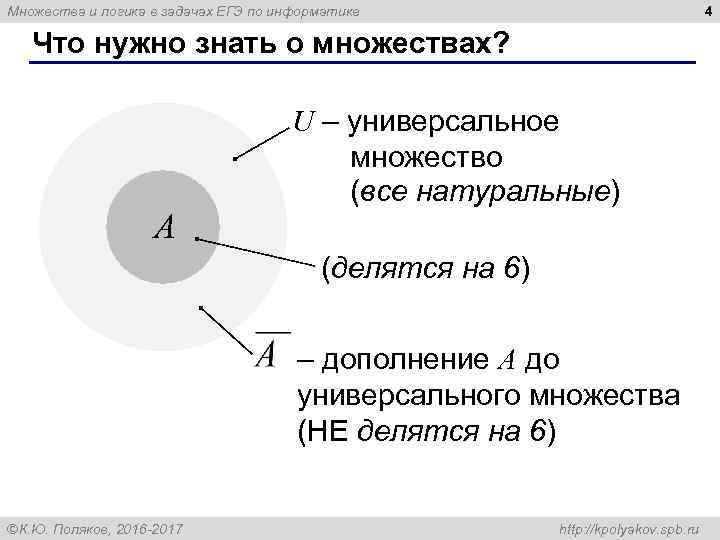4 Множества и логика в задачах ЕГЭ по информатике Что нужно знать о множествах? A U – универсальное множество (все натуральные) (делятся на 6) – дополнение A до универсального множества (НЕ делятся на 6) ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
5 Множества и логика в задачах ЕГЭ по информатике Что нужно знать о множествах? A B A∙B – пересечение (A B) A B A+B – объединение (A B) ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
6 Множества и логика в задачах ЕГЭ по информатике Множества и логические функции Множество задаётся логической функцией A x A A(x) = 1 A A B ÓК. Ю. Поляков, 2016 -2017 x A∙B x A+B http: //kpolyakov. spb. ru
7 Множества и логика в задачах ЕГЭ по информатике Базовые задачи (ЕГЭ) Задача 1. Каким должно быть множество A для того, чтобы множество A + B совпадало с универсальным множеством? Другие решения: ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
8 Множества и логика в задачах ЕГЭ по информатике Базовые задачи (ЕГЭ) Задача 2. Каким должно быть множество A для того, чтобы множество совпадало с универсальным множеством? ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
9 Множества и логика в задачах ЕГЭ по информатике Общий подход к решению 1. Свести задачу к одной из базовых задач Задача 1. Задача 2. Использовать готовое решение: Задача 1. Задача 2. ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
10 Множества и логика в задачах ЕГЭ по информатике Задачи с отрезками На числовой прямой даны два отрезка: P = [37; 60] и Q = [40; 77]. Укажите наименьшую возможную длину такого отрезка A, что выражение (x P) → (((x Q) ¬(x A)) → ¬(x P)) истинно при любом значении переменной х. Вводим утверждения: P = (x P), Q = (x Q), A = (x A) Заданное условие: ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
11 Множества и логика в задачах ЕГЭ по информатике Задачи с отрезками Упрощение выражения: Задача 1 Решение: P = [37; 60], Q = [40; 77] Amin = [40; 60] ÓК. Ю. Поляков, 2016 -2017 длина 20 http: //kpolyakov. spb. ru
12 Множества и логика в задачах ЕГЭ по информатике Задачи с отрезками-II На числовой прямой даны два отрезка: P = [10; 20] и Q = [25; 55]. Укажите наибольшую возможную длину такого отрезка A, что выражение (x A) → ((x P) (x Q)) истинно при любом значении переменной х. Вводим утверждения: P = (x P), Q = (x Q), A = (x A) Заданное условие: ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
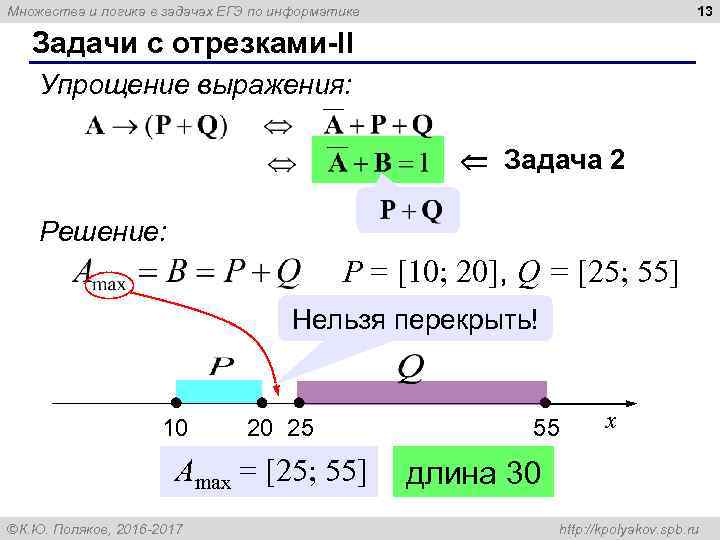13 Множества и логика в задачах ЕГЭ по информатике Задачи с отрезками-II Упрощение выражения: Задача 2 Решение: P = [10; 20], Q = [25; 55] Нельзя перекрыть! 10 20 25 Amax = [25; 55] ÓК. Ю. Поляков, 2016 -2017 55 x длина 30 http: //kpolyakov. spb. ru
14 Множества и логика в задачах ЕГЭ по информатике Множества чисел Элементами множеств А, P и Q являются натуральные числа, причём P = {2, 4, 6, 8, 10, 12} и Q = {4, 8, 12, 116}. Известно, что выражение (x P) → (((x Q) ¬(x A)) → ¬(x P)) истинно при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A. Вводим утверждения: P = (x P), Q = (x Q), A = (x A) Заданное условие: ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
15 Множества и логика в задачах ЕГЭ по информатике Множества чисел Упрощение выражения: Задача 1 Решение: P = {2, 4, 6, 8, 10, 12}, Q = {4, 8, 12, 116} Amin = {4, 8, 12} ÓК. Ю. Поляков, 2016 -2017 сумма 24 http: //kpolyakov. spb. ru
16 Множества и логика в задачах ЕГЭ по информатике Множества чисел-II Элементами множеств А, P и Q являются натуральные числа, причём P = { 2, 4, 6, 8, 10, 12, 14, 16, 18, 20} Q = { 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 }. Известно, что выражение ((x A) → ¬(x P)) (¬(x Q) → ¬(x A)) истинно при любом значении переменной х. Определите наибольшее возможное количество элементов множества A. Вводим утверждения: P = (x P), Q = (x Q), A = (x A) Заданное условие: ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
17 Множества и логика в задачах ЕГЭ по информатике Множества чисел-II Упрощение выражения: Решение: Задача 2 P = { 2, 4, 6, 8, 10, 12, 14, 16, 18, 20} Q = { 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 } Amax = { 3, 9, 15, 21, 24, 27, 30 } ÓК. Ю. Поляков, 2016 -2017 7 шт. http: //kpolyakov. spb. ru
18 Множества и логика в задачах ЕГЭ по информатике Делимость Для какого наибольшего натурального числа a выражение ¬ДЕЛ(x, a) (ДЕЛ(x, 6) ¬ДЕЛ(x, 4)) тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной х)? DN – множество чисел, делящихся на N A = Da – множество чисел, делящихся на a Вводим утверждения: DN = (x DN), A = (x A) Заданное условие: ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
19 Множества и логика в задачах ЕГЭ по информатике Делимость Упрощение выражения: Задача 1 Решение: D 6∙D 4 = D 12 D 6∙D 4 A=Da max 12 Одновременно делятся на 6 и на 4! любой делитель 12! ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
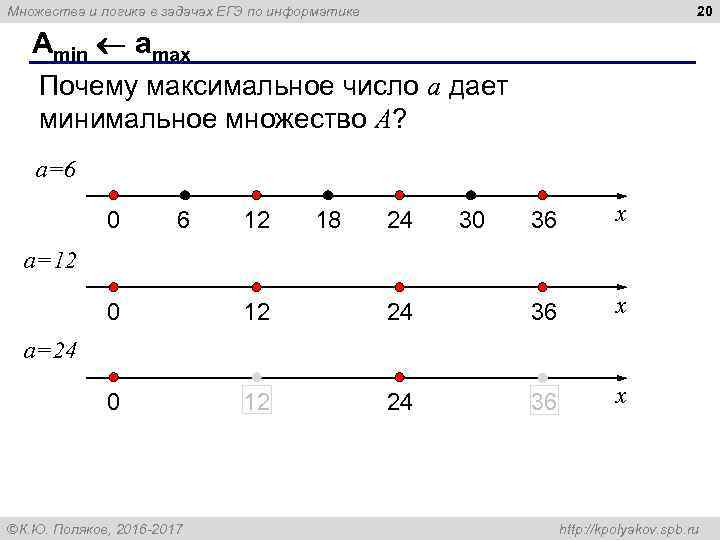20 Множества и логика в задачах ЕГЭ по информатике Amin amax Почему максимальное число a дает минимальное множество A? a=6 0 6 12 18 24 30 36 x a=12 0 12 24 36 x a=24 ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
21 Множества и логика в задачах ЕГЭ по информатике Делимость-II Для какого наибольшего натурального числа a выражение ¬ДЕЛ(x, a) (¬ ДЕЛ(x, 21) ¬ДЕЛ(x, 35)) тождественно истинно? DN – множество чисел, делящихся на N A = Da – множество чисел, делящихся на a Вводим утверждения: DN = (x DN), A = (x A) Заданное условие: ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
22 Множества и логика в задачах ЕГЭ по информатике Делимость-II Упрощение выражения: Задача 1 Решение: D 21+D 35 = Da D 21+D 35 < Da Делятся на 21 или на 35! нет такого a! max Общий делитель 21 и 35! ÓК. Ю. Поляков, 2016 -2017 7 http: //kpolyakov. spb. ru
23 Множества и логика в задачах ЕГЭ по информатике Делимость-III Для какого наименьшего натурального числа a выражение ДЕЛ(x, a) (¬ ДЕЛ(x, 21) ДЕЛ(x, 35)) тождественно истинно? DN – множество чисел, делящихся на N A = Da – множество чисел, делящихся на a Вводим утверждения: DN = (x DN), A = (x A) Заданное условие: ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
24 Множества и логика в задачах ЕГЭ по информатике Делимость-III Упрощение выражения: Задача 2 Решение: нет такого a! ÓК. Ю. Поляков, 2016 -2017 Не делятся на 21 или делятся на 35! http: //kpolyakov. spb. ru
25 Множества и логика в задачах ЕГЭ по информатике Делимость-III Переход к другой импликации: ! Если число делится на a и на 21, оно должно делиться на 35! Делится на A и на 21: k, m – натуральные Делится на 35: Этот сомножитель добавляется с помощью A! ÓК. Ю. Поляков, 2016 -2017 min 5 http: //kpolyakov. spb. ru
26 Множества и логика в задачах ЕГЭ по информатике Делимость-IV Для какого наименьшего натурального числа a выражение (ДЕЛ(x, a) ДЕЛ(x, 21)) ДЕЛ(x, 18) тождественно истинно? DN – множество чисел, делящихся на N A = Da – множество чисел, делящихся на a Вводим утверждения: DN = (x DN), A = (x A) Заданное условие: ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
27 Множества и логика в задачах ЕГЭ по информатике Делимость-IV ! Если число делится на A и на 21, оно должно делиться на 18! Делится на A и на 21: Делится на 18: Эти сомножители добавляются с помощью A! ÓК. Ю. Поляков, 2016 -2017 min 18 http: //kpolyakov. spb. ru
28 Множества и логика в задачах ЕГЭ по информатике Делимость-V Для какого наименьшего натурального числа a выражение ¬ДЕЛ(x, 18) (¬ДЕЛ(x, 21) ¬ДЕЛ(x, a)) тождественно истинно? DN – множество чисел, делящихся на N A = Da – множество чисел, делящихся на a Вводим утверждения: DN = (x DN), A = (x A) Заданное условие: ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
29 Множества и логика в задачах ЕГЭ по информатике Делимость-IV Задача 2 Решение: нет такого a! Делятся на 18 или на 21! Варианты: ! Нельзя перекрывать другие числа! ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
30 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции Определите наименьшее натуральное число a, такое что выражение (x & 53 0) ((x & 41 = 0) (x & a 0)) тождественно истинно. ? Вводим множества: ZN = {x: x & N = 0} Вводим утверждения: ZN = (x ZN), A = (x Za) Заданное условие: ÓК. Ю. Поляков, 2016 -2017 Число a определяет множество Za или условие A. http: //kpolyakov. spb. ru
31 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции Что такое Z 53: биты 5 4 3 2 1 0 53 = 110101 x = abcdef x & 53 = ab 0 d 0 f = 0 Что такое : биты 5 4 3 2 1 0 53 = 110101 x = abcdef x & 53 = ab 0 d 0 f 0 ÓК. Ю. Поляков, 2016 -2017 Биты 5, 4, 2, 0 числа x нулевые! Среди битов 5, 4, 2, 0 числа x есть ненулевые! http: //kpolyakov. spb. ru
32 Множества и логика в задачах ЕГЭ по информатике Главная ошибка После упрощения: биты 5 4 3 2 1 0 21 = 010101 11 = 001011 Вывод: Натуральные числа! ! ? ÓК. Ю. Поляков, 2016 -2017 Логические значения! Это ИНОГДА проходит! Это min или max? http: //kpolyakov. spb. ru
33 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции биты 5 4 3 2 1 0 53 = 110101 Z 53 30 = 011110 Z 30 63 = 111111 = 53 or 30 ÓК. Ю. Поляков, 2016 -2017 Биты 5, 4, 2, 0 числа x нулевые! Биты 4, 3, 2, 1 числа x нулевые! http: //kpolyakov. spb. ru
34 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции биты 5 4 3 2 1 0 53 = 110101 Z 53 30 = 011110 Z 30 20 = 010100 = 53 and 30 Биты 5, 4, 2, 0 числа x нулевые! Биты 4, 3, 2, 1 числа x нулевые! Только в одну сторону! ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
35 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции Двойственность операций И и ИЛИ Доказательство: только для левой части импликации! От противного: ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
36 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции Биты 4, 2 и 0 нулевые! биты 4 3 2 1 0 21 = 10101 ! Биты 4 и 0 нулевые! биты 4 3 2 1 0 17 = 10001 Множество единичных битов c входит во множество единичных битов b! 0 биты 4 3 2 1 0 21 = 10101 ÓК. Ю. Поляков, 2016 -2017 биты 4 3 2 1 0 1 7 = 00111 http: //kpolyakov. spb. ru
37 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции ? Для каких x? Если в числе x не равен 0 хотя бы один бит, который равен 1 в b or c ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
Множества и логика в задачах ЕГЭ по информатике 38 Побитовые логические операции Вариант 1: Вариант 2: ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
39 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции Вариант 1: ! a – любое! Вариант 2: ! Множество единичных битов a входит во множество единичных битов b! ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
40 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции Метод А. В. Здвижковой (г. Армавир): ! Строим импликацию так, чтобы избавиться от всех инверсий! ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
41 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции Биты 5, 3, 0 нулевые! Решение: Логическое ИЛИ между битами! биты 5 4 3 2 1 0 41 = 101001 a = ? ? ? 1 1 53 = 110101 amin = 101002 = 20 ÓК. Ю. Поляков, 2016 -2017 Биты 5, 4, 2, 0 нулевые! ? Другие a? http: //kpolyakov. spb. ru
42 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции-II Определите наибольшее натуральное число a, такое что выражение (x & a 0) ((x & 20 = 0) (x & 5 0)) тождественно истинно. Вводим множества: ZN = {x: x & N = 0} Вводим утверждения: ZN = (x ZN), A = (x Za) Заданное условие: ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
43 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции-II Упрощение выражения (до суммы): Импликация без инверсий: Решение: биты 4 3 2 1 0 Биты 4, 2 нулевые! 20 = 10100 5 = 00101 amax = 101012 = 21 a = 1, 4, 5, 16, 17, 20, 21 Биты 2, 0 нулевые! ? ? Другие a? Сколько? 23 – 1 = 7 ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
44 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции-III Определите наибольшее натуральное число a, такое что выражение (x & a 0) ((x & 12 = 0) (x & 21 = 0)) тождественно истинно. Вводим множества: ZN = {x: x & N = 0} Вводим утверждения: ZN = (x ZN), A = (x Za) Заданное условие: ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
45 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции-III Упрощение выражения: ! От него ничего не зависит! Решение: биты 4 3 2 1 0 12 = 1100 1 21 = 1 10101 ? amax = 11002 = 12 Другие a? a = 4, 8, 12 22 – 1 = 3 ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
46 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции-IV Определите наименьшее натуральное число a, такое что выражение ( (x & 28 0) (x & 45 0)) ((x & 48 = 0) (x & a 0)) тождественно истинно. Вводим множества: ZN = {x: x & N = 0} Вводим утверждения: ZN = (x ZN), A = (x Za) Заданное условие: ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
47 Множества и логика в задачах ЕГЭ по информатике Побитовые операции–IV Упрощение выражения: Решение: биты 5 4 3 2 1 0 28 = 11100 45 = 101101 = 111101 48 = 110000 11 1 a = ? ? ? = 111101 ÓК. Ю. Поляков, 2016 -2017 Логическое ИЛИ между битами! ? Другие a? amin = 11012 = 13 http: //kpolyakov. spb. ru
48 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции (V) (А. Г. Гильдин). Определите наименьшее натуральное число a, такое что выражение (x & 19 = 0) (x & 38 0) ((x & 43 = 0) ((x & a = 0) (x & 43 = 0))) тождественно истинно. Вводим множества: ZN = {x: x & N = 0} Вводим утверждения: ZN = (x ZN), A = (x Za) Заданное условие: ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
49 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции (V) Упрощение выражения: ! Решение: биты 5 4 3 2 1 0 ? 43 = 101011 Какие подходят? Все, у которых единицы только в разрядах 5, 3, 1 и 0! a = 1, 2, 3, 8, 9, 10, 11, 32, 33, 34, 35, 40, 41, 42, 43 ÓК. Ю. Поляков, 2016 -2017 Не влияют на решение! 24 – 1 = 15 http: //kpolyakov. spb. ru
50 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции (VI) (М. В. Кузнецова). Определите наименьшее натуральное число a, такое что выражение (( (x & 13 0) (x & a 0)) (x & 13 0) ((x & a 0) (x & 39 = 0)) тождественно истинно. Вводим множества: ZN = {x: x & N = 0} Вводим утверждения: ZN = (x ZN), A = (x Za) Заданное условие: ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
51 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции (V) Упрощение выражения: Решение: биты 5 4 3 2 1 0 13 = 1101 1 39 = 1 100111 ÓК. Ю. Поляков, 2016 -2017 ! Не влияет на решение! a = 1, 4, 5, 8, 9, 12, 13 http: //kpolyakov. spb. ru
52 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции (V) Вариант с другими числами: Решение: биты 5 4 3 2 1 0 53 = 110101 21 = 10101 ! ! Всегда 1! a – любое! Множество единичных битов числа 21 входит во множество единичных битов числа 53! ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
53 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции (VI) Определите наименьшее натуральное число a, такое что выражение ((x & 23 0) (x & 45 0)) ((x & a 0) (x & 23 0)) тождественно истинно. Вводим множества: ZN = {x: x & N = 0} Вводим утверждения: ZN = (x ZN), A = (x Za) Заданное условие: ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
54 Множества и логика в задачах ЕГЭ по информатике Побитовые логические операции (V) Упрощение выражения: или ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru
55 Множества и логика в задачах ЕГЭ по информатике Нерешаемая задача Попытка решения: биты 5 4 3 2 1 0 43 = 101011 a = ? ? ? 1 48 = 110000 ! ÓК. Ю. Поляков, 2016 -2017 Логическое ИЛИ между битами! С помощью a можно добавить биты, но нельзя убрать! http: //kpolyakov. spb. ru
56 Множества и логика в задачах ЕГЭ по информатике Конец фильма ПОЛЯКОВ Константин Юрьевич д. т. н. , учитель информатики ГБОУ СОШ № 163, г. Санкт-Петербург kpolyakov@mail. ru ÓК. Ю. Поляков, 2016 -2017 http: //kpolyakov. spb. ru