К лекции 5. Проведение эксперимента и обработка его результатов.
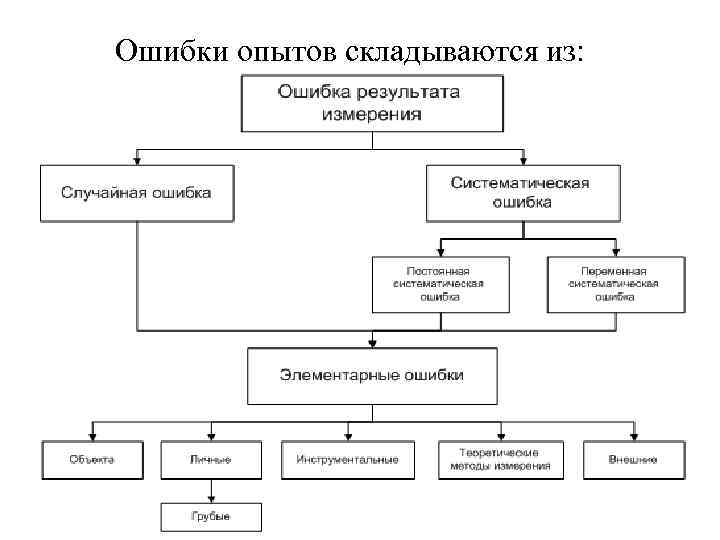
Ошибки опытов складываются из:
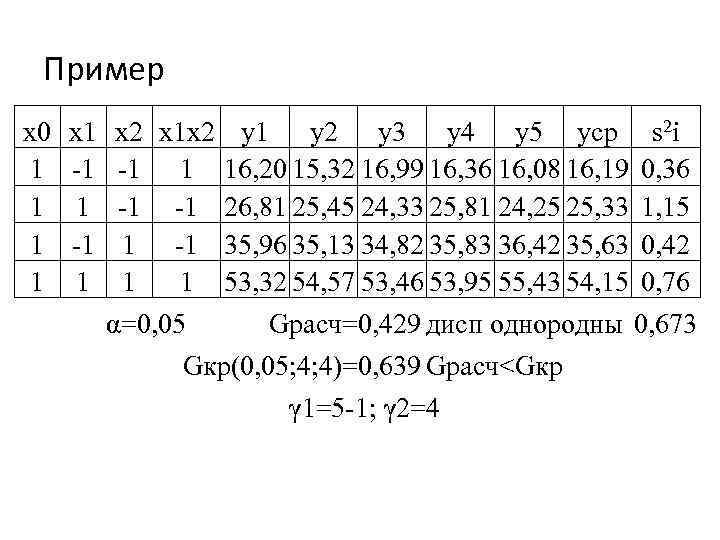
Пример x 0 1 1 x 1 -1 1 x 2 x 1 x 2 y 1 y 2 y 3 y 4 y 5 yср s 2 i -1 1 16, 20 15, 32 16, 99 16, 36 16, 08 16, 19 0, 36 -1 -1 26, 81 25, 45 24, 33 25, 81 24, 25 25, 33 1, 15 1 -1 35, 96 35, 13 34, 82 35, 83 36, 42 35, 63 0, 42 1 1 53, 32 54, 57 53, 46 53, 95 55, 43 54, 15 0, 76 α=0, 05 Gрасч=0, 429 дисп однородны 0, 673 Gкр(0, 05; 4; 4)=0, 639 Gрасч<Gкр γ 1=5 -1; γ 2=4
МНК Для ПФЭ 22 матрица будет иметь вид
Вектор значений откликов: Вектор оценок уравнения регрессии: Уравнение регрессии: Y=ФВ. коэффициентов
Умножим обе части равенства на ФT: Отсюда можно выразить вектор коэффициентов регрессии: Матрица обладает свойствами симметричности, ортогональности, нормировки.
Матрицу называют информационной матрицей. Для ПФЭ 22 :
В общем виде , где m =2 k.
Корреляционная матрица факторов, включенных в эксперимент равна
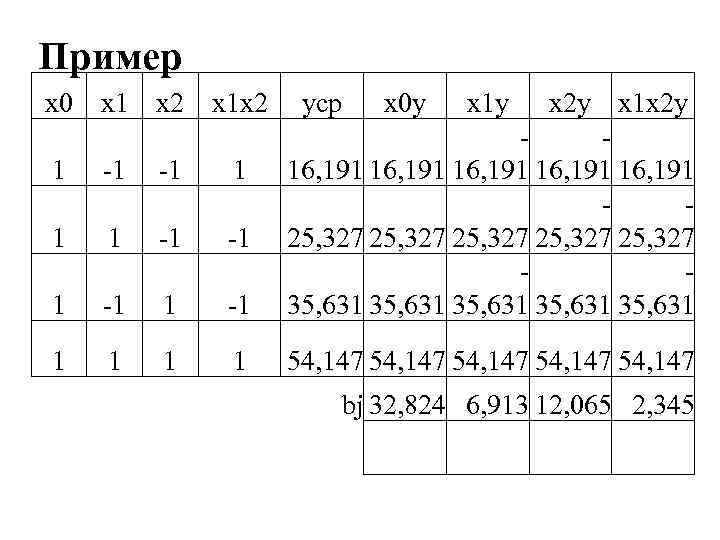
Пример x 0 x 1 x 2 x 1 x 2 yср x 0 y x 1 y 1 -1 -1 1 -1 x 2 y x 1 x 2 y 16, 191 16, 191 25, 327 25, 327 35, 631 35, 631 1 1 54, 147 54, 147 bj 32, 824 6, 913 12, 065 2, 345
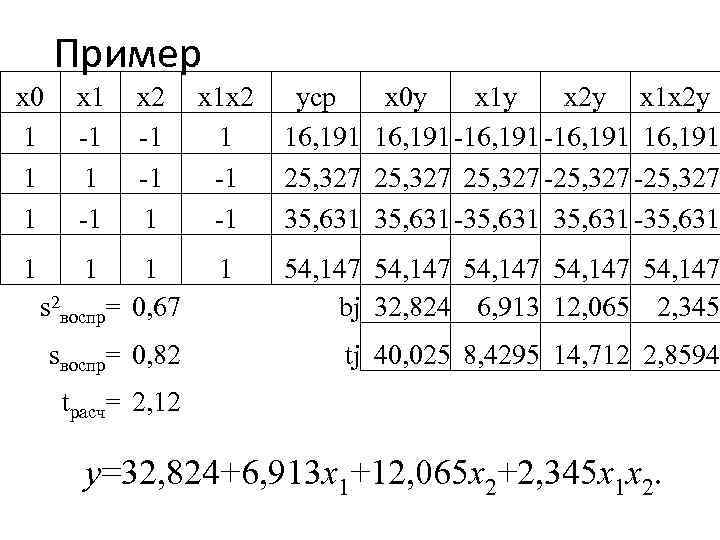
Пример x 0 1 1 1 x 1 -1 1 x 2 -1 -1 1 s 2 воспр= 0, 67 sвоспр= 0, 82 x 1 x 2 1 -1 -1 1 yср 16, 191 25, 327 35, 631 x 0 y x 1 y x 2 y x 1 x 2 y 16, 191 -16, 191 25, 327 -25, 327 35, 631 -35, 631 54, 147 54, 147 bj 32, 824 6, 913 12, 065 2, 345 tj 40, 025 8, 4295 14, 712 2, 8594 tрасч= 2, 12 y=32, 824+6, 913 x 1+12, 065 x 2+2, 345 x 1 x 2.
Проверка адекватности регрессионной модели. Для проверки адекватности достаточно оценить отклонение предсказанного уравнением регрессии значения отклика от результатов эксперимента. Для этого вычисляют дисперсию адекватности или остаточную дисперсию: – число значимых коэффициентов модели. ,
Если s 2 ост не превышает дисперсии опыта s 2 y, то полученная математическая модель адекватно представляет результаты эксперимента, иначе – описание считается неадекватным объекту. F-критерий Фишера:
По уровню значимости α и числам степеней свободы γ 1=k-1 и γ 2=n-k-1 определяется критическое значение F(α, γ 1, γ 2). Если , то уравнение регрессии считается адекватным. В случае, если и неравенство выполняться всегда. , то будет
Проверка адекватности с помощью критерия Фишера возможна, если s 2 ост>0. При n=m не остается степеней свободы для проверки нуль-гипотезы об адекватности. yср 16, 191 25, 327 35, 631 yt 16, 191 25, 327 35, 631 54, 147 s 2 ост=0 Модель адекватна.
Скачать презентацию К лекции 5 Проведение эксперимента и обработка его
К лекции 5 обр эксп.ppt