2e29616ee8ed3345747fdfc7502e8fca.ppt
- Количество слайдов: 23

JASS’ 02 A-Salt, Jordan, October 2002 The structure of liquid surfaces Moshe Deutsch Physics Department, Bar-Ilan University, Ramat-Gan 52900, Israel OUTLINE Why bother ? ( motivation & history ) How to bother ? ( experimental) Was it worth bothering ? ( some of the results) Should we keep bothering ? (future directions)

2 Motivation & History On the one hand: Ø Bulk liquids are boring: no order, no defects, no phases/transitions. . . density Ø Theory very difficult: No comprehensive theory to date. The surface of a boring bulk must be a boring surface : depth On the other hand: Ø Liquid surfaces have attracted interest (not always scientific) since ancient times. ( Bible, China, Greece, Ben Franklin …. ) Ø X-ray methods developed only in 1982 -6. Ø Increasing number of studies since then. Atomic resolution liquid surface studies reveal many new and intriguing effects ! The art of lecanomancy (Hamurabi, 18 th century B. C. E. ) The spreading of oil on water in a ceremonial bowl (1) Oil sinks, rises and spreads: war-lost sick- divine punishment (2) Oil splits in two: war-both camps march together sick- death (3) Single oil drop emerges in the east: war-booty sick-recovery (4) 2 drops (large & small): male child will be born sick- recovery (5) Oil fills bowl: war-defeat for the leader sick- death
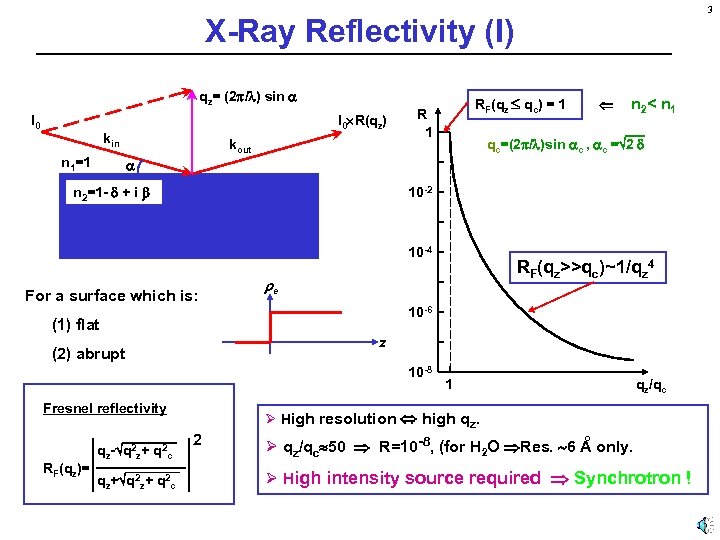
3 X-Ray Reflectivity (I) qz= (2 / ) sin I 0 R(qz) kin n 1=1 kout RF(qz qc) = 1 R 1 n 2< n 1 qc=(2 / )sin c , c = 2 n 2=1 - + i 10 -2 10 -4 For a surface which is: 10 -6 z (2) abrupt 10 -8 Fresnel reflectivity qz- q 2 z+ q 2 c qz+ q 2 c RF(qz>>qc)~1/qz 4 e (1) flat RF(qz)= 1 qz/qc Ø High resolution high qz. 2 º Ø qz/qc 50 R=10 -8, (for H 2 O Res. 6 A only. Ø High intensity source required Synchrotron !
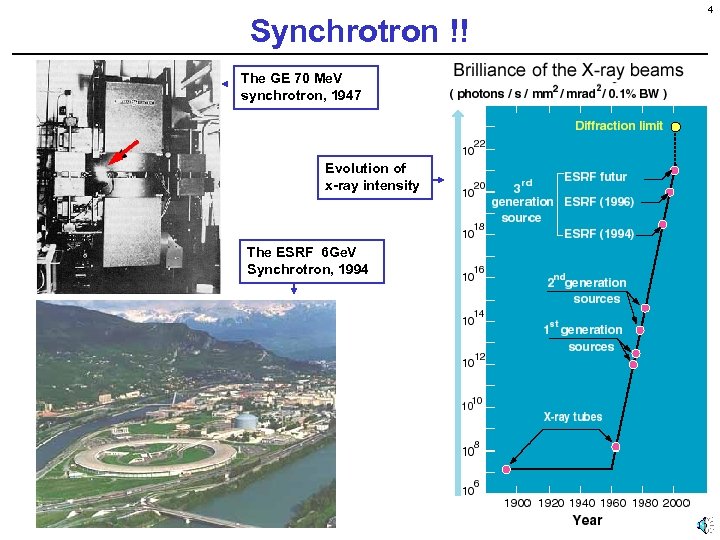
Synchrotron !! The GE 70 Me. V synchrotron, 1947 Evolution of x-ray intensity The ESRF 6 Ge. V Synchrotron, 1994 4
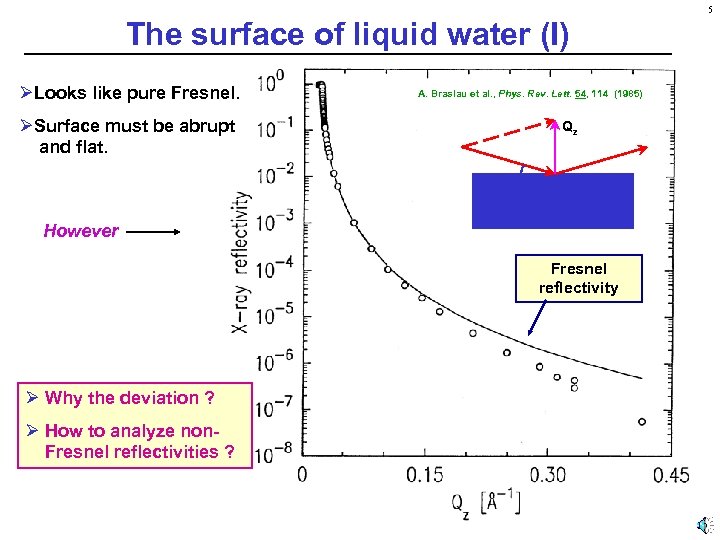
5 The surface of liquid water (I) ØLooks like pure Fresnel. ØSurface must be abrupt and flat. A. Braslau et al. , Phys. Rev. Lett. 54, 114 (1985) Qz However Fresnel reflectivity Ø Why the deviation ? Ø How to analyze non. Fresnel reflectivities ?
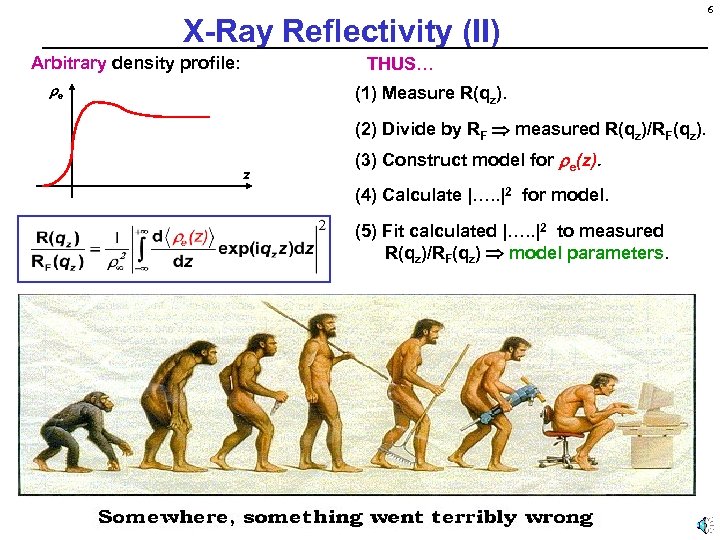
X-Ray Reflectivity (II) Arbitrary density profile: THUS… e (1) Measure R(qz). (2) Divide by RF measured R(qz)/RF(qz). z (3) Construct model for e(z). (4) Calculate |…. . |2 for model. (5) Fit calculated |…. . |2 to measured R(qz)/RF(qz) model parameters. 6
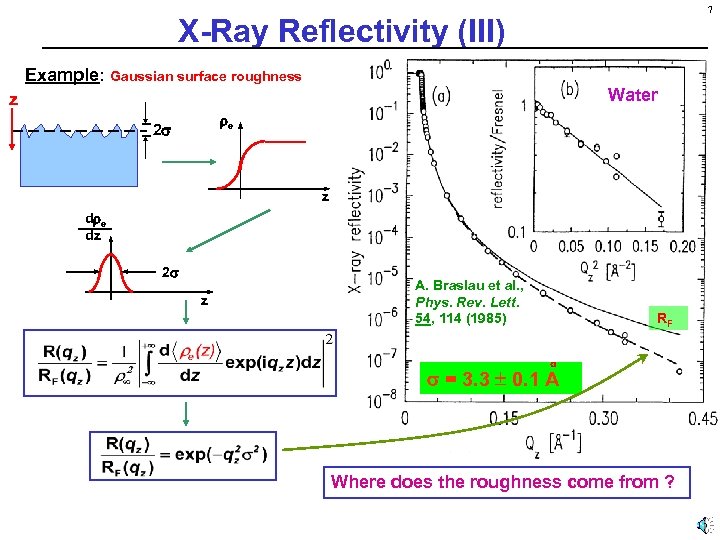
7 X-Ray Reflectivity (III) Example: Gaussian surface roughness Water z e 2 z d e dz 2 z A. Braslau et al. , Phys. Rev. Lett. 54, 114 (1985) RF = 3. 3 0. 1 A Where does the roughness come from ?

Capillary waves (I) Where does the roughness come from ? A. Braslau et al. , Phys. Rev. Lett. 54, 114 (1985) Thermally excited capillary waves are common to all liquid surfaces. Start with: (x, y) x Equipartition of surface energy and averaging over all modes yields: Cutoffs are determined by the atomic size (qmax) and resolution or gravitation (qmin). Taking into account non-capillary contributions: ° Using this for water yields = 3. 2 A ! 8
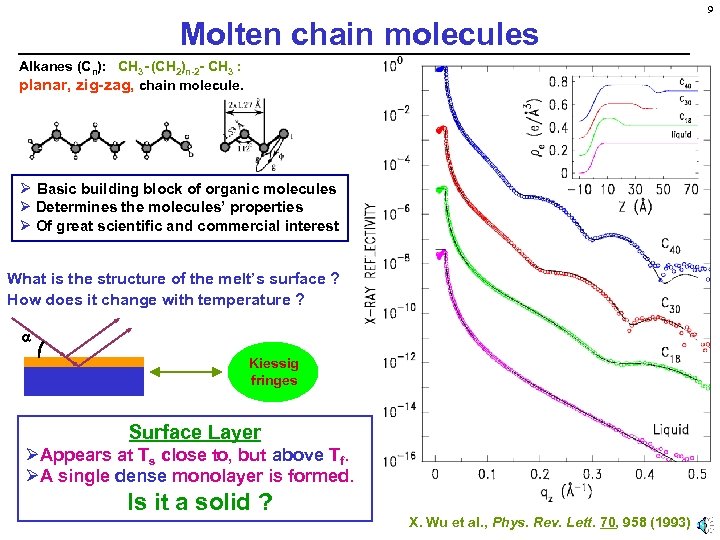
9 Molten chain molecules Alkanes (Cn): CH 3 - (CH 2)n-2 - CH 3 : planar, zig-zag, chain molecule. Ø Basic building block of organic molecules Ø Determines the molecules’ properties Ø Of great scientific and commercial interest What is the structure of the melt’s surface ? How does it change with temperature ? Kiessig fringes Surface Layer ØAppears at Ts close to, but above Tf. ØA single dense monolayer is formed. Is it a solid ? X. Wu et al. , Phys. Rev. Lett. 70, 958 (1993)
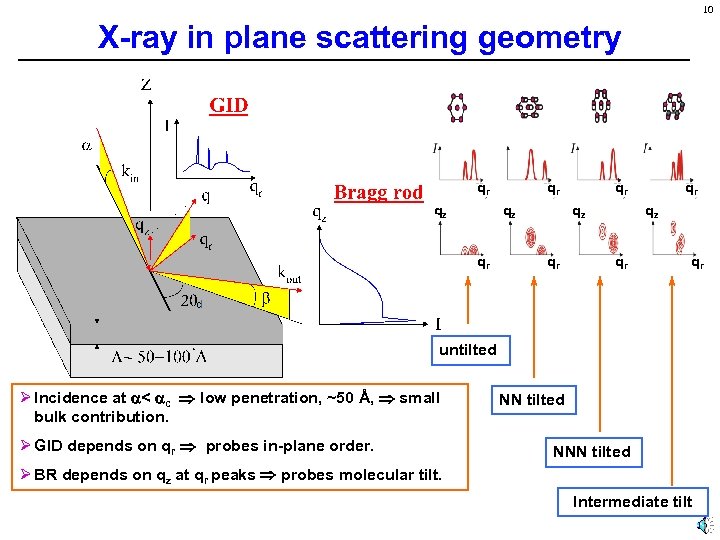
10 X-ray in plane scattering geometry qr qz qr qr untilted Ø Incidence at < c low penetration, ~50 Å, small bulk contribution. Ø GID depends on qr probes in-plane order. NN tilted NNN tilted Ø BR depends on qz at qr peaks probes molecular tilt. Intermediate tilt
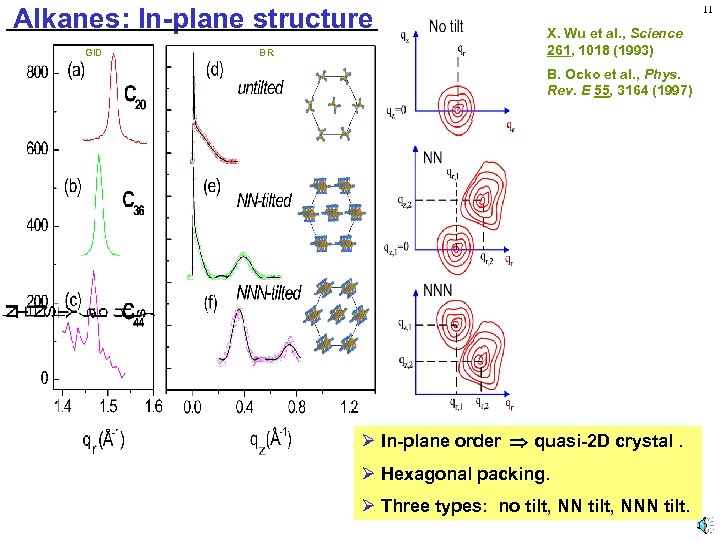
Alkanes: In-plane structure GID BR 11 X. Wu et al. , Science 261, 1018 (1993) B. Ocko et al. , Phys. Rev. E 55, 3164 (1997) Ø In-plane order quasi-2 D crystal. Ø Hexagonal packing. Ø Three types: no tilt, NNN tilt.
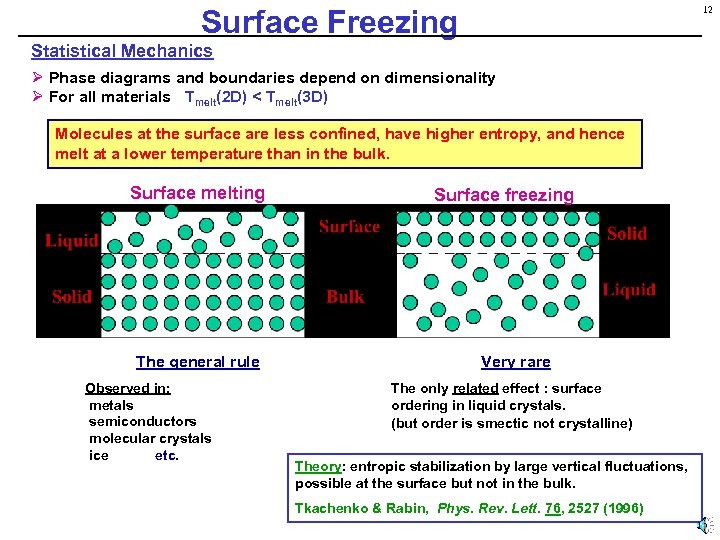
Surface Freezing 12 Statistical Mechanics Ø Phase diagrams and boundaries depend on dimensionality Ø For all materials Tmelt(2 D) < Tmelt(3 D) Molecules at the surface are less confined, have higher entropy, and hence melt at a lower temperature than in the bulk. Surface melting The general rule Observed in: metals semiconductors molecular crystals ice etc. Surface freezing Very rare The only related effect : surface ordering in liquid crystals. (but order is smectic not crystalline) Theory: entropic stabilization by large vertical fluctuations, possible at the surface but not in the bulk. Tkachenko & Rabin, Phys. Rev. Lett. 76, 2527 (1996)
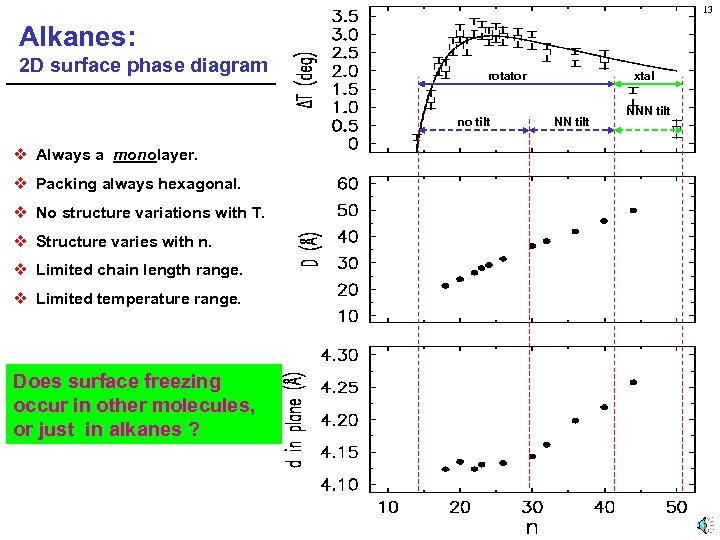
13 Alkanes: 2 D surface phase diagram rotator no tilt v Always a monolayer. v Packing always hexagonal. v No structure variations with T. v Structure varies with n. v Limited chain length range. v Limited temperature range. Does surface freezing occur in other molecules, or just in alkanes ? xtal NN tilt NNN tilt
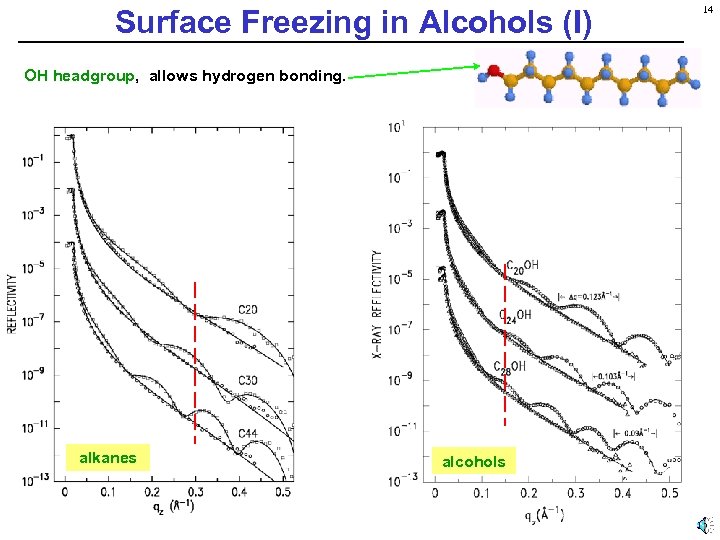
Surface Freezing in Alcohols (I) OH headgroup, allows hydrogen bonding. alkanes alcohols 14
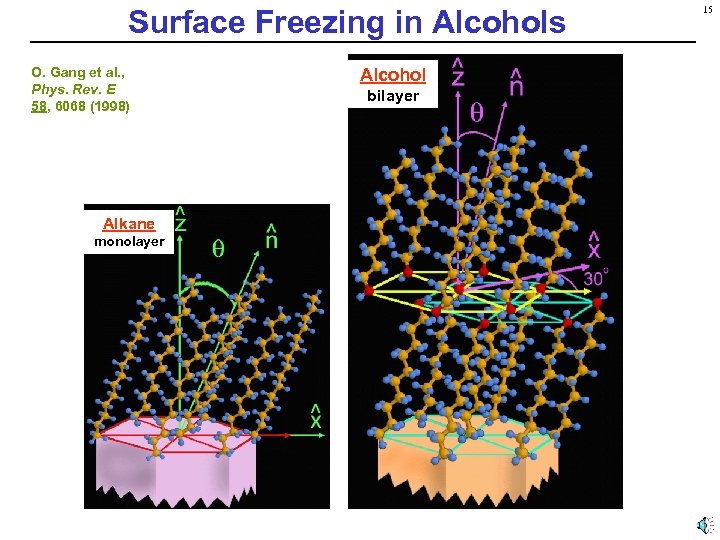
Surface Freezing in Alcohols O. Gang et al. , Phys. Rev. E 58, 6068 (1998) Alkane monolayer Alcohol bilayer 15
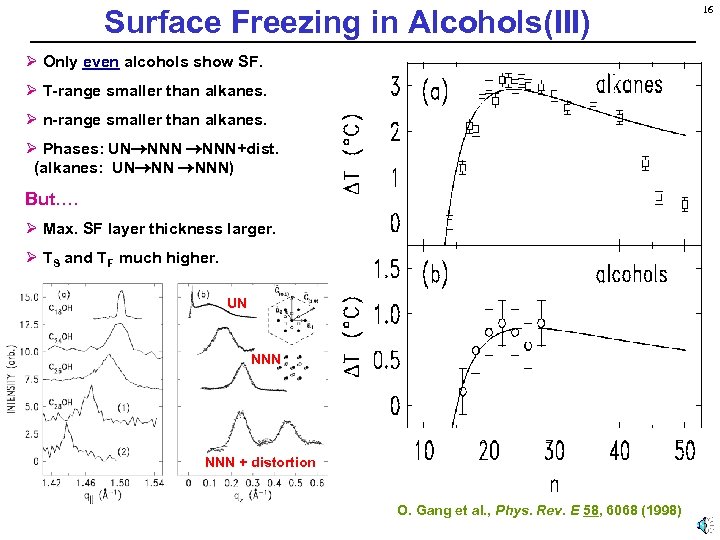
Surface Freezing in Alcohols(III) Ø Only even alcohols show SF. Ø T-range smaller than alkanes. Ø n-range smaller than alkanes. Ø Phases: UN NNN+dist. (alkanes: UN NN NNN) But…. Ø Max. SF layer thickness larger. Ø TS and TF much higher. UN NNN + distortion O. Gang et al. , Phys. Rev. E 58, 6068 (1998) 16
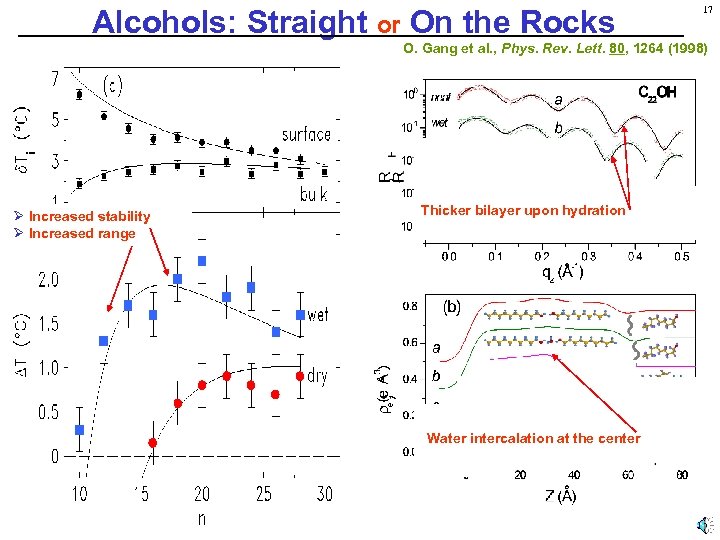
Alcohols: Straight or On the Rocks 17 O. Gang et al. , Phys. Rev. Lett. 80, 1264 (1998) Ø Increased stability Ø Increased range Thicker bilayer upon hydration Water intercalation at the center
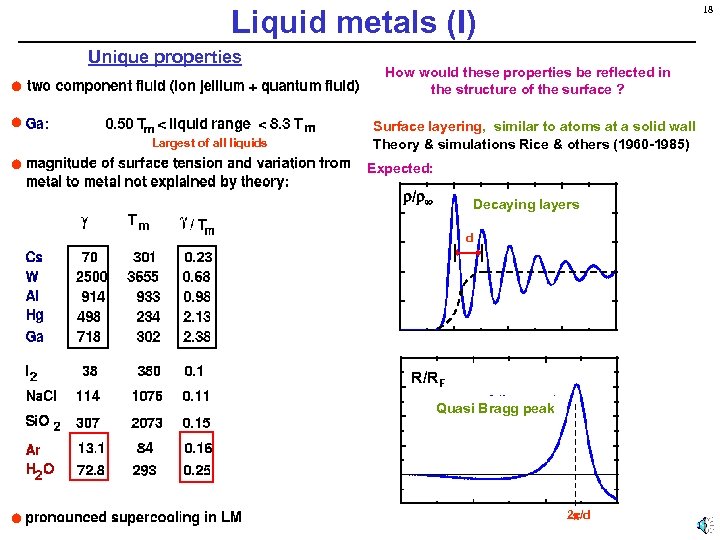
Liquid metals (I) Unique properties Largest of all liquids 18 How would these properties be reflected in the structure of the surface ? Surface layering, similar to atoms at a solid wall Theory & simulations Rice & others (1960 -1985) Expected: / Decaying layers d R/RF Quasi Bragg peak 2 /d
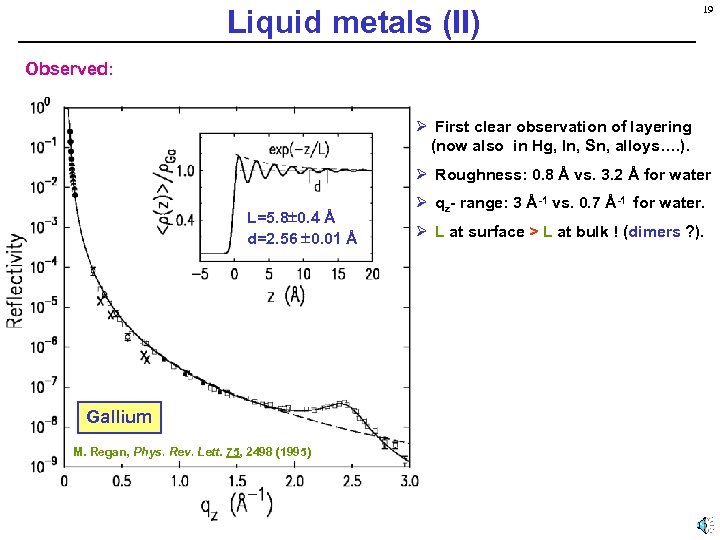
Liquid metals (II) 19 Observed: Ø First clear observation of layering (now also in Hg, In, Sn, alloys…. ). Ø Roughness: 0. 8 Å vs. 3. 2 Å for water L=5. 8 0. 4 Å d=2. 56 0. 01 Å Gallium M. Regan, Phys. Rev. Lett. 75, 2498 (1995) Ø qz- range: 3 Å-1 vs. 0. 7 Å-1 for water. Ø L at surface > L at bulk ! (dimers ? ).
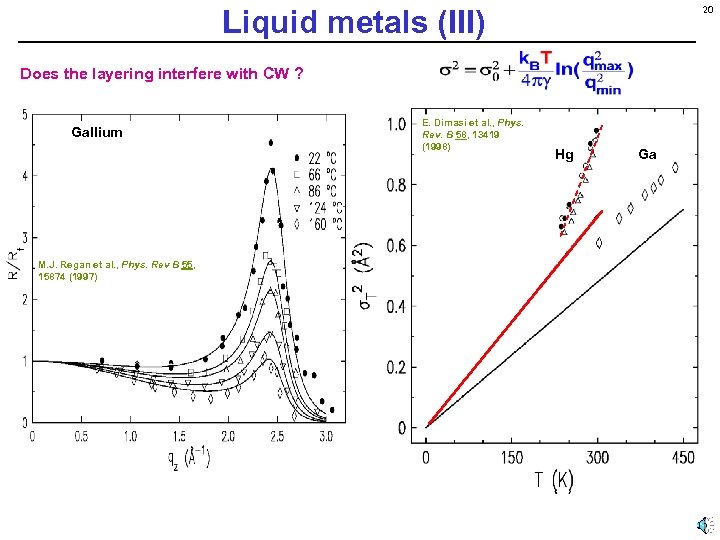
Liquid metals (III) 20 Does the layering interfere with CW ? Gallium E. Dimasi et al. , Phys. Rev. B 58, 13419 (1998) Hg M. J. Regan et al. , Phys. Rev B 55, 15874 (1997) Observed: Ga

21 What was left out…………. . Because of time limitaion many current studies were left out: v The surface structure of van der Waals liquids (organic liquids etc. ). v The structure of liquid alloys. v Wetting in binary liquid mixtures (long range, short range). v Adsorbed Gibbs layers at the liquid surface. v Overlayers on water: Langmuir films. v Overlayers on metals: surface oxidation, organics monolayers on metals. v The structure of the liquid-liquid interface. v The structure of a solid-liquid interface.

22 Thanks …… Water Ø A. Braslau, B. Ocko, A. Weiss, P. Pershan (Harvard), J. Als-Nielsen, J. Bohr (Risø) Liquid metals Ø N. Maskil, H. Kraack (Bar-Ilan), M. Regan, H. Tostmann, P. Pershan (Harvard), O. Magnussen, E. Di. Masi, B. Ocko (BNL) Surface Freezing Ø O. Gang, H. Kraack, E. Sloutskin (Bar-Ilan), X. Wu, E. Sirota (Exxon), B. Ocko (BNL) $$$$$$ (actually ¢¢¢) Beamtime: Israel: U. S. -Israel BSF, ISF, Exxon U. S. : DOE, NSF NSLS, Brookhaven National Laboratory APS, Argonne National Laboratory HASYLAB, Hamburg, Germany ESRF, Grenoble, France

23 One of my previous talks at the University of ……
2e29616ee8ed3345747fdfc7502e8fca.ppt