ИЗУЧЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИХ ОСНОВ КАНЦЕРОГЕНЕЗА С ПОМОЩЬЮ ДОМЕННООРИЕНТИРОВАННОГО ПОДХОДА

ИЗУЧЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИХ ОСНОВ КАНЦЕРОГЕНЕЗА С ПОМОЩЬЮ ДОМЕННООРИЕНТИРОВАННОГО ПОДХОДА Борисов Н. М. Федеральный медицинский биофизический центр им. А. И. Бурназяна ФМБА России

Международная коллаборация • Thomas Jefferson University (Philadelphia, USA): Boris Kholodenko, Anatoly Kiyatkin, Edita Aksamitiene, Nikolai Markevich, Jan Hoek, Marc Birthwitsle et. al. • Humboldt-University (Berlin, Germany): Stefan Legewie • University of Freiburg (Germany): Thomas Maiwald • University of Pittsburgh (USA): Jim Faeder • RIKEN (JAPAN): Mariko Hatakeyama et al. • Институт биофизики клетки РАН (Пущино, Россия): Н. П. Каймачников, М. Цыганов • ФМБЦ им. А. И. Бурназяна (Москва, Россия): Н. М. Борисов, А. С. Чистопольский и др.

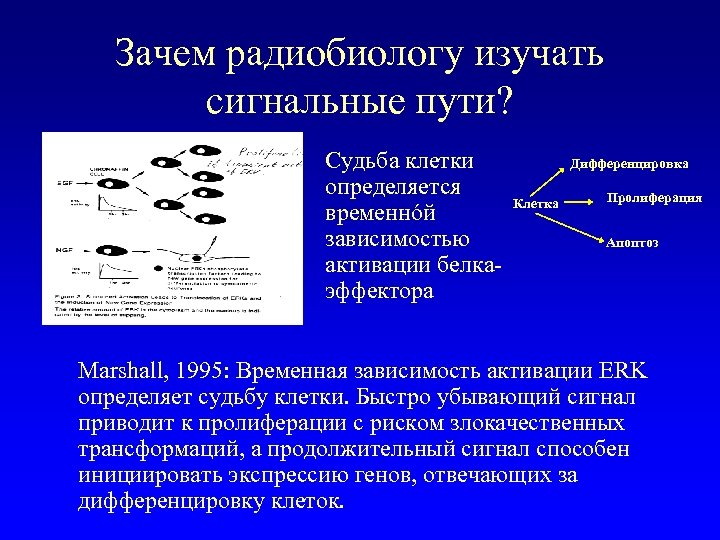Зачем радиобиологу изучать сигнальные пути? Судьба клетки определяется временнóй зависимостью активации белкаэффектора Дифференцировка Клетка Пролиферация Апоптоз Marshall, 1995: Временная зависимость активации ERK определяет судьбу клетки. Быстро убывающий сигнал приводит к пролиферации с риском злокачественных трансформаций, а продолжительный сигнал способен инициировать экспрессию генов, отвечающих за дифференцировку клеток.

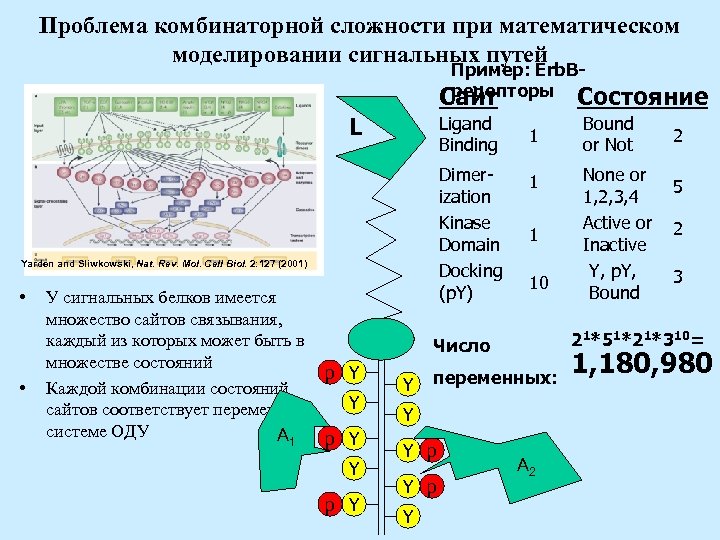Проблема комбинаторной сложности при математическом моделировании сигнальных путей Пример: Erb. Bрецепторы Состояние Сайт L Ligand Binding Dimerization Kinase Domain Docking (p. Y) Yarden and Sliwkowski, Nat. Rev. Mol. Cell Biol. 2: 127 (2001) • • У сигнальных белков имеется множество сайтов связывания, каждый из которых может быть в множестве состояний p Y Каждой комбинации состояний Y сайтов соответствует переменная в системе ОДУ A 1 p Y Y p Y 1 10 переменных: Y Y p Y None or 1, 2, 3, 4 Active or Inactive Y, p. Y, Bound 2 5 2 3 21*51*21*310= Число Y Bound or Not A 2 1, 180, 980

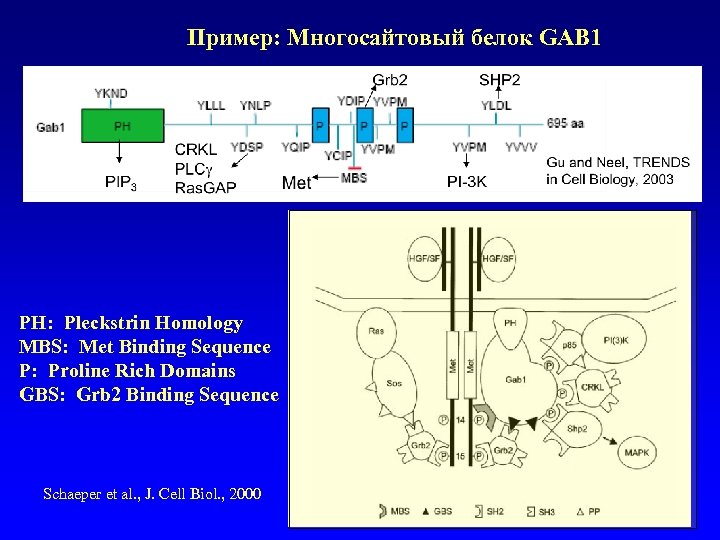Пример: Многосайтовый белок GAB 1 PH: Pleckstrin Homology MBS: Met Binding Sequence P: Proline Rich Domains GBS: Grb 2 Binding Sequence Schaeper et al. , J. Cell Biol. , 2000

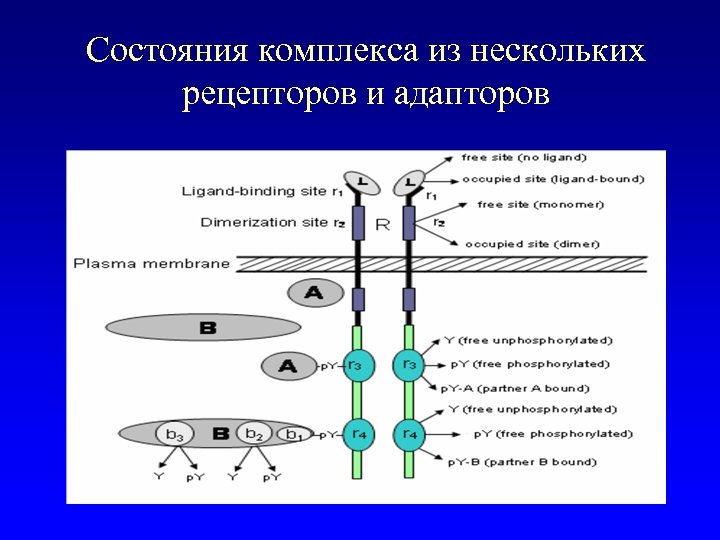Состояния комплекса из нескольких рецепторов и адапторов

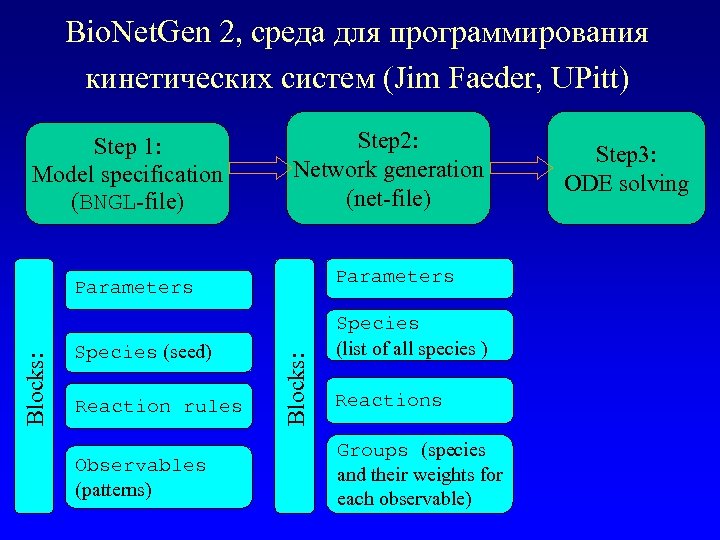Bio. Net. Gen 2, среда для программирования кинетических систем (Jim Faeder, UPitt) Step 1: Model specification (BNGL-file) Step 2: Network generation (net-file) Parameters Species (seed) Reaction rules Observables (patterns) Blocks: Parameters Species (list of all species ) Reactions Groups (species and their weights for each observable) Step 3: ODE solving

Два предельных случая • Абсолютно конкурентное связывание партнеров на многоцентровых белках. Удобно для моделирования: нет комбинаторной сложности • Абсолютно независимое связывание партнеров на многоцентровых белках. Необходимы методы уменьшения числа переменных! Промежуточный случай – наличие аллостерических взаимодействий между партнерами (с точки зрения моделирования самый неудобный): основной метод – ограничение числа молекул в комплексе.

Доменно-ориентированный подход к сокращению числа переменных Borisov et al. , Biophys J, 2005; Bio. Systems, 2006: S – многосайтовый адаптор, R – рецепторная тирозин-киназа, A 1 and A 2 – партнеры белка S Если связывание A 1 and A 2 происходит независимо, то: Доменно-ориентированное (макро-) описание: 12 переменных и 14 реакций Механистическое (микро-) описание: 18 переменных, 33 реакции

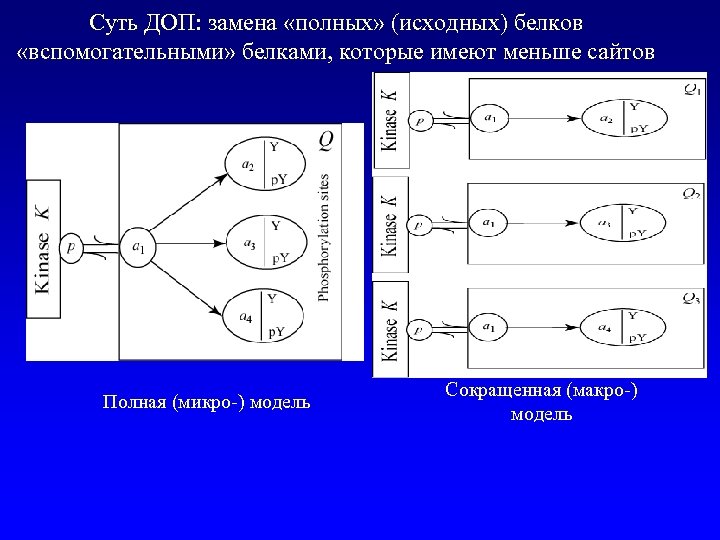Суть ДОП: замена «полных» (исходных) белков «вспомогательными» белками, которые имеют меньше сайтов Полная (микро-) модель Сокращенная (макро-) модель

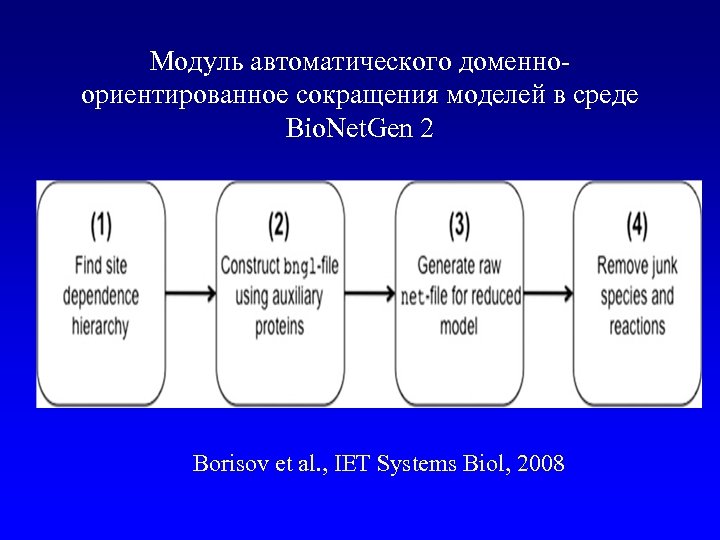Модуль автоматического доменноориентированное сокращения моделей в среде Bio. Net. Gen 2 Borisov et al. , IET Systems Biol, 2008

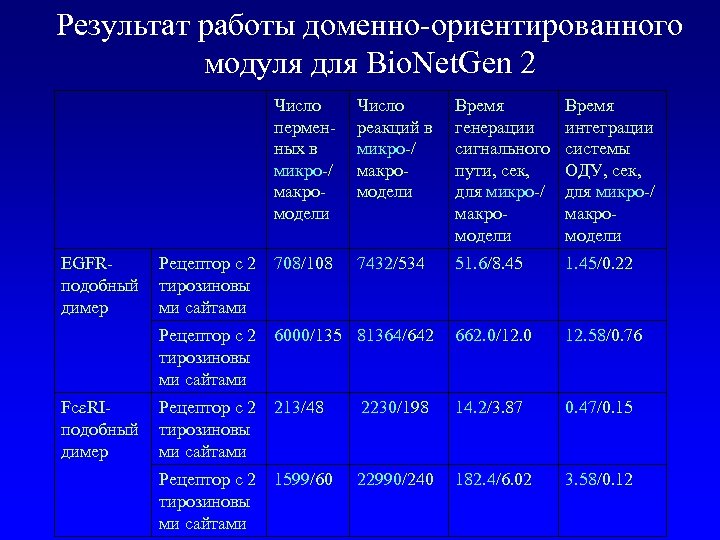Результат работы доменно-ориентированного модуля для Bio. Net. Gen 2 Число перменных в микро-/ макромодели FcεRIподобный димер Время генерации сигнального пути, сек, для микро-/ макромодели Время интеграции системы ОДУ, сек, для микро-/ макромодели 7432/534 51. 6/8. 45 1. 45/0. 22 Рецептор с 2 6000/135 81364/642 тирозиновы ми сайтами EGFRподобный димер Число реакций в микро-/ макромодели 662. 0/12. 0 12. 58/0. 76 Рецептор с 2 213/48 тирозиновы ми сайтами 2230/198 14. 2/3. 87 0. 47/0. 15 Рецептор с 2 1599/60 тирозиновы ми сайтами 22990/240 182. 4/6. 02 3. 58/0. 12 Рецептор с 2 708/108 тирозиновы ми сайтами

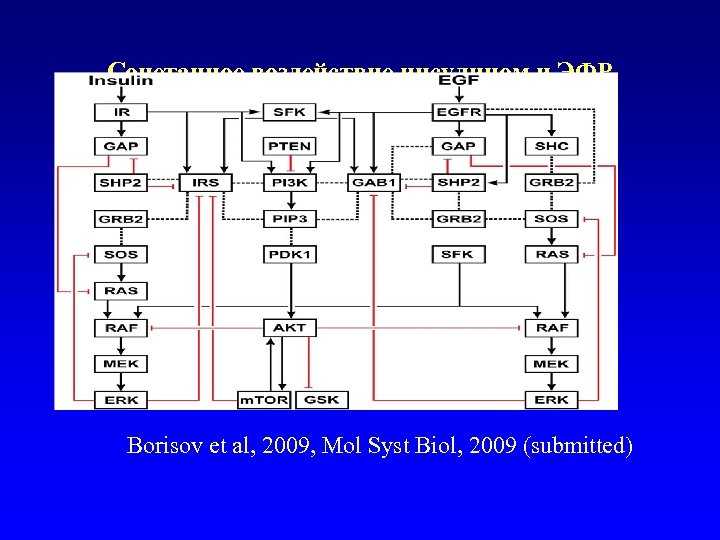Сочетанное воздействие инсулином и ЭФР Borisov et al, 2009, Mol Syst Biol, 2009 (submitted)

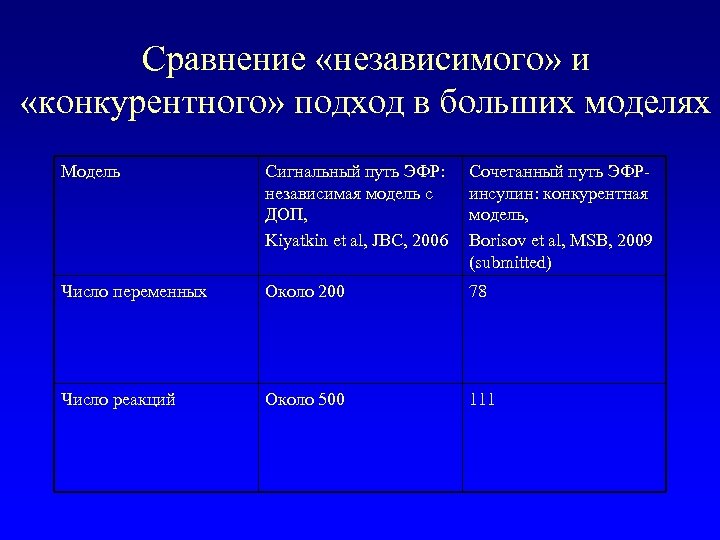Сравнение «независимого» и «конкурентного» подход в больших моделях Модель Сигнальный путь ЭФР: независимая модель с ДОП, Kiyatkin et al, JBC, 2006 Сочетанный путь ЭФРинсулин: конкурентная модель, Borisov et al, MSB, 2009 (submitted) Число переменных Около 200 78 Число реакций Около 500 111

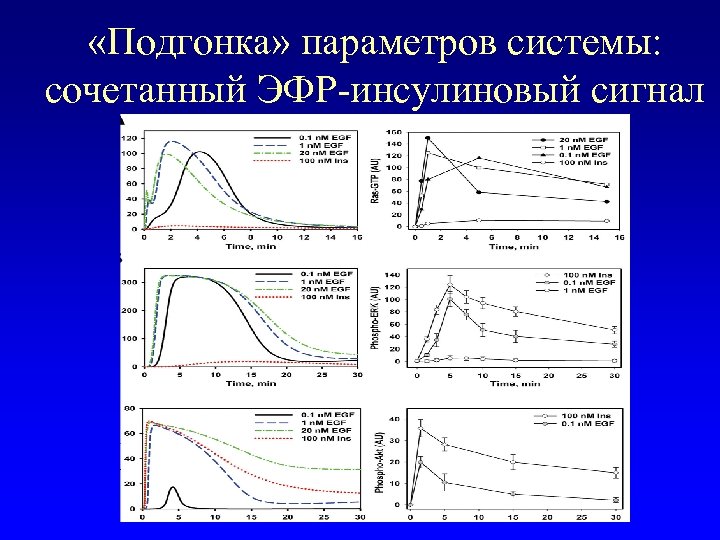«Подгонка» параметров системы: сочетанный ЭФР-инсулиновый сигнал

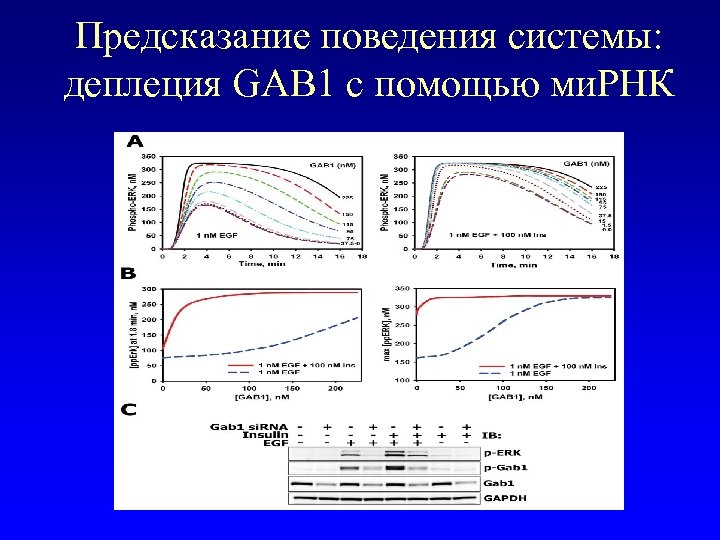Предсказание поведения системы: деплеция GAB 1 c помощью ми. РНК

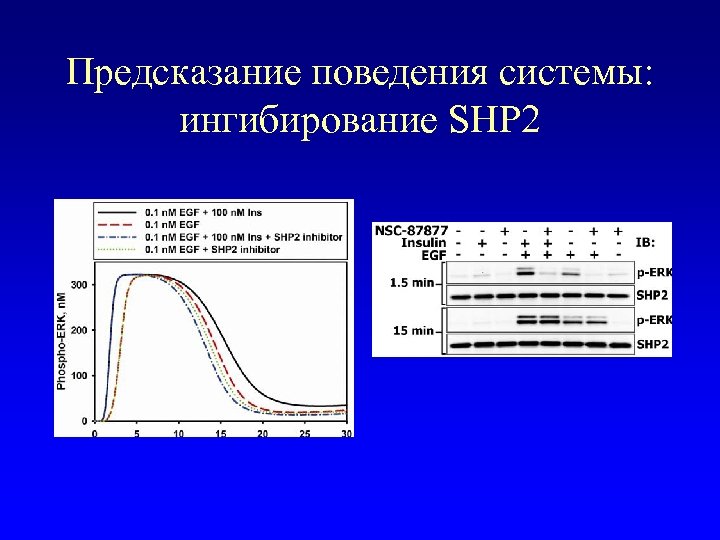Предсказание поведения системы: ингибирование SHP 2

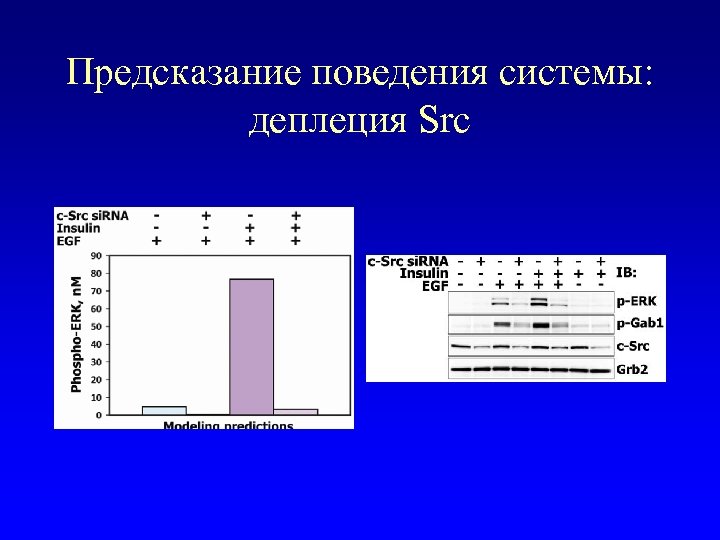Предсказание поведения системы: деплеция Src

Философский вопрос: нужны ли большие модели в биологии 1. Вычислительная математика «выросла» из «прямых» задач (таких, как задача Коши и др. ), для решения которых «законы природы» были известны и просты (законы Ньютона в физике, закон действующих масс в химии). 2. В биологии «законы природы» сложнее и не всегда известны, поэтому для их исследования почти всегда приходится решать «обратные» зачади вычислительной математики.

Проблема свободных параметров 4. Астрономия началась с неверной гипотезы о «законах природы» (геоцентризм). Она, тем не менее, укладывалась в тогдашние наблюдения. 5. К эпохе Возрождения возникла проблема несоответствия наблюдаемых данных и птолемеевского геоцентризма. 6. В эпоху Возрождения было предложено два подхода к астрономии – пересмотр парадигмы (Коперник. Кеплер-Ньютон) и подгонак свобюодных параметров под геоцентризм (Тихо Браге.

Проблема свободных параметров 7. Любую математическую модель можно «втиснуть» в совокупность экспериментальных данных за счет свободных параметров, но ценность такой модели сомнительна. 8. Значит, ценная математическая модель должна давать нетривиальные экспериментально проверяемые предсказания после подгонки свободных параметров