4_Изоморфизм и гомоморфизм.ppt
- Количество слайдов: 16
 Изоморфизм и гомоморфизм групп Определение. Группы G 1 и G 2 называются гомоморфными, если существует отображение : G 1 G 2, сохраняющее операции, определенные в G 1 и G 2. Т. е. , для
Изоморфизм и гомоморфизм групп Определение. Группы G 1 и G 2 называются гомоморфными, если существует отображение : G 1 G 2, сохраняющее операции, определенные в G 1 и G 2. Т. е. , для
 Примеры. 1) G 1 =
Примеры. 1) G 1 =
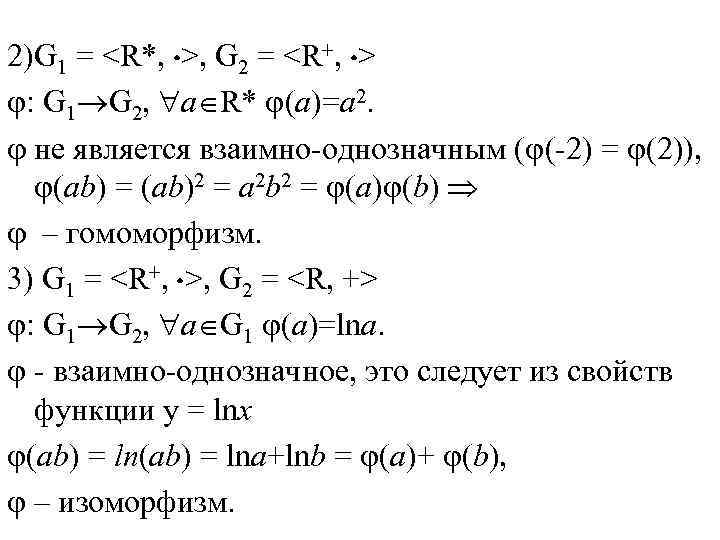 2)G 1 =
2)G 1 =
 Свойства изоморфизма Т 1. Изоморфный образ группы является группой. Дано:
Свойства изоморфизма Т 1. Изоморфный образ группы является группой. Дано:
 3) Существование нейтрального элемента. Пусть e - нейтральный элемент из G 1. Покажем, что (e) – нейтральный элемент G 2. Т. е. b G 2 b○ (e) = (e)○b = b. Т. к. - изоморфизм, то a G 1, (a) = b. b○ (e) = (a)○ (e) = (a) = b (e)○b = (e)○ (a) = (e a) = (a) = b b○ (e) = (e)○b = b, следовательно (e) – нейтральный элемент G 2. 4) Нейтрализующий элемент. b G 2 b-1 G 2, b○b-1 = e', e' = (e) – нейтральный элемент G 2. (a) = b. Покажем, что (a-1) = b-1. b○b-1 = (a)○ (a-1) = (a a-1) = (e) = e' G 2, b-1○b = (a-1)○ (a) = (a-1 a) = (e) = e'.
3) Существование нейтрального элемента. Пусть e - нейтральный элемент из G 1. Покажем, что (e) – нейтральный элемент G 2. Т. е. b G 2 b○ (e) = (e)○b = b. Т. к. - изоморфизм, то a G 1, (a) = b. b○ (e) = (a)○ (e) = (a) = b (e)○b = (e)○ (a) = (e a) = (a) = b b○ (e) = (e)○b = b, следовательно (e) – нейтральный элемент G 2. 4) Нейтрализующий элемент. b G 2 b-1 G 2, b○b-1 = e', e' = (e) – нейтральный элемент G 2. (a) = b. Покажем, что (a-1) = b-1. b○b-1 = (a)○ (a-1) = (a a-1) = (e) = e' G 2, b-1○b = (a-1)○ (a) = (a-1 a) = (e) = e'.
 Т 2. Любая бесконечная циклическая группа изоморфна аддитивной группе целых чисел. Дано: G = – циклическая; |G| = |a| = . Доказать: G
Т 2. Любая бесконечная циклическая группа изоморфна аддитивной группе целых чисел. Дано: G = – циклическая; |G| = |a| = . Доказать: G
 Т 3. Любая циклическая группа порядка m изоморфна аддитивной группе классов вычетов по модулю m. Дано: G = – циклическая; |G| = |a| = m. Доказать: G
Т 3. Любая циклическая группа порядка m изоморфна аддитивной группе классов вычетов по модулю m. Дано: G = – циклическая; |G| = |a| = m. Доказать: G
 Т 4. Конечная циклическая группа порядка n изоморфна мультипликативной группе корней n-ой степени из единицы Дано: G = – циклическая группа; |G| = |a| = n. Доказать: G
Т 4. Конечная циклическая группа порядка n изоморфна мультипликативной группе корней n-ой степени из единицы Дано: G = – циклическая группа; |G| = |a| = n. Доказать: G
 1) Взаимная однозначность. а) Пусть am 1 = am 2 am 1 -m 2 =e св-ва порядка m 1 = m 2 + nt, t Z. (am 1) = (am 2). б) Пусть (am 1) = (am 2), т. е. тогда
1) Взаимная однозначность. а) Пусть am 1 = am 2 am 1 -m 2 =e св-ва порядка m 1 = m 2 + nt, t Z. (am 1) = (am 2). б) Пусть (am 1) = (am 2), т. е. тогда
 2) Сохранение операций: (am 1 am 2) = (am 1+m 2) =
2) Сохранение операций: (am 1 am 2) = (am 1+m 2) =
 Т 5 (Кэли). Любая конечная группа порядка n изоморфна некоторой подгруппе подстановок n -ой степени. Дано: G – группа; |G| = n. Доказать: Н Sn такая, что G H. Доказательство: G = {a 1, a 2, …, an, } ai G рассмотрим произведения a 1 ai, a 2 ai, …, an ai G. Все эти произведения будут различными Обозначим: a 1 ai = a 1, a 2 ai = a 2, … an ai = a n. 1, 2, …, n - некоторый набор чисел от 1 до n. Рассмотрим отображение Покажем, что – изоморфизм.
Т 5 (Кэли). Любая конечная группа порядка n изоморфна некоторой подгруппе подстановок n -ой степени. Дано: G – группа; |G| = n. Доказать: Н Sn такая, что G H. Доказательство: G = {a 1, a 2, …, an, } ai G рассмотрим произведения a 1 ai, a 2 ai, …, an ai G. Все эти произведения будут различными Обозначим: a 1 ai = a 1, a 2 ai = a 2, … an ai = a n. 1, 2, …, n - некоторый набор чисел от 1 до n. Рассмотрим отображение Покажем, что – изоморфизм.
 1) Взаимная однозначность. а) Пусть ai = aj из однозначности произведения (ai) = (aj) б) Пусть (ai) = (aj). Тогда k, k=1, 2, …, n ak ai = ak aj ai = aj. 2) Для доказательства сохранения операции будем использовать подстановку: Тогда
1) Взаимная однозначность. а) Пусть ai = aj из однозначности произведения (ai) = (aj) б) Пусть (ai) = (aj). Тогда k, k=1, 2, …, n ak ai = ak aj ai = aj. 2) Для доказательства сохранения операции будем использовать подстановку: Тогда
![Ядро гомоморфизма (kernel ['kə: nəl]) Пусть : G 1 G 2; –гомоморфизм. Определение. Ядром Ядро гомоморфизма (kernel ['kə: nəl]) Пусть : G 1 G 2; –гомоморфизм. Определение. Ядром](https://present5.com/presentation/3/154154717_166247568.pdf-img/154154717_166247568.pdf-13.jpg) Ядро гомоморфизма (kernel ['kə: nəl]) Пусть : G 1 G 2; –гомоморфизм. Определение. Ядром гомоморфизма называется множество элементов группы G 1, которые отображаются в нейтральный элемент группы G 2. G 1 G 2 e´ Обозн. : Ker = {a G 1 / (a) =e', e' G 2}.
Ядро гомоморфизма (kernel ['kə: nəl]) Пусть : G 1 G 2; –гомоморфизм. Определение. Ядром гомоморфизма называется множество элементов группы G 1, которые отображаются в нейтральный элемент группы G 2. G 1 G 2 e´ Обозн. : Ker = {a G 1 / (a) =e', e' G 2}.
 Т 1. Ядро гомоморфизма является нормальным делителем группы. Дано: G – группа, H = Ker . Доказать: H G. Доказательство: 1) Покажем, что H G а) a, b H ab H. Пусть a, b H, тогда (a) = (b) = e'. (ab) = – гомоморфизм (a) (b) = e' e' = e' ab H. б) Пусть a H, тогда (a) = e'. Найдем (a-1) = ( (a))-1 = (e')-1 = e' a-1 H. 2) Покажем, что H G, т. е. a G a. H = Ha. Пусть ah a. H, покажем, что h 1 a Ha, такой, что ah=h 1 a. Рассмотрим aha-1 и найдем его образ: (aha-1) = (a) (h) (a-1) = (a) e (a-1) = (a a-1) = (e) = e'. Тогда aha-1 H или aha-1=h 1 ah=h 1 a.
Т 1. Ядро гомоморфизма является нормальным делителем группы. Дано: G – группа, H = Ker . Доказать: H G. Доказательство: 1) Покажем, что H G а) a, b H ab H. Пусть a, b H, тогда (a) = (b) = e'. (ab) = – гомоморфизм (a) (b) = e' e' = e' ab H. б) Пусть a H, тогда (a) = e'. Найдем (a-1) = ( (a))-1 = (e')-1 = e' a-1 H. 2) Покажем, что H G, т. е. a G a. H = Ha. Пусть ah a. H, покажем, что h 1 a Ha, такой, что ah=h 1 a. Рассмотрим aha-1 и найдем его образ: (aha-1) = (a) (h) (a-1) = (a) e (a-1) = (a a-1) = (e) = e'. Тогда aha-1 H или aha-1=h 1 ah=h 1 a.
 Т 2. Любая нормальная подгруппа группы G является ядром некоторого гомоморфизма. Дано: H G Доказать: H – ядро некоторого гомоморфизма. Доказательство: G/H={H, g 1 H, g 2 H, …}. : G G/H g G (g) = g H. Покажем, что – гомоморфизм ( – сохраняет операцию). g 1, g 2 G (g 1 g 2) = (g 1 g 2) H = (g 1 g 2)H H = g 1 H g 2 H = (g 1) (g 2) – гомоморфизм. Покажем, что H = Ker . Пусть h H (h) = h H = H – нейтральный элемент G/H. Следовательно, h Ker и H Ker (1) Пусть h 1 Ker (h 1) = H или h 1 H = H h 1 H Ker H (2). Из (1) и (2) следует ч. т. д. Определение. Гомоморфизм группы G на факторгруппу G/H называется естественным гомоморфизмом группы G.
Т 2. Любая нормальная подгруппа группы G является ядром некоторого гомоморфизма. Дано: H G Доказать: H – ядро некоторого гомоморфизма. Доказательство: G/H={H, g 1 H, g 2 H, …}. : G G/H g G (g) = g H. Покажем, что – гомоморфизм ( – сохраняет операцию). g 1, g 2 G (g 1 g 2) = (g 1 g 2) H = (g 1 g 2)H H = g 1 H g 2 H = (g 1) (g 2) – гомоморфизм. Покажем, что H = Ker . Пусть h H (h) = h H = H – нейтральный элемент G/H. Следовательно, h Ker и H Ker (1) Пусть h 1 Ker (h 1) = H или h 1 H = H h 1 H Ker H (2). Из (1) и (2) следует ч. т. д. Определение. Гомоморфизм группы G на факторгруппу G/H называется естественным гомоморфизмом группы G.
 Т 3. Гомоморфный образ группы изоморфен факторгруппе по ядру этого гомоморфизма. Дано: : G 1 G 2; – гомоморфизм, H = Ker . Доказать: G 1/H G 2. Доказательство: Рассмотрим отображение : G 1/H G 2 такое, что g H G 1/H (g H) = (g); g G 1; (g) G 2. Покажем, что – изоморфизм. 1. Взаимная однозначность. Пусть g 1 H = g 2 H (g 2 -1 g 1)H = H g 2 -1 g 1 H, т. е. g 2 -1 g 1 Ker (g 2 -1 g 1) = e' G 2. Т. к. – гомоморфизм, (g 2 -1) (g 1) = e' или ( (g 2))-1 (g 1) = e' (g 1) = (g 2) (g 1 H) = (g 2 H). Обратно, пусть (g 1 H) = (g 2 H), или (g 1) = (g 2), ( (g 2))-1 (g 1) = e' G 2 (g 2 -1 g 1) = e'. Тогда g 2 -1 g 1 Ker = H или (g 2 -1 g 1)H = H g 1 H = g 2 H. 2. Сохранение операции. (g 1 H g 2 H) = ((g 1 g 2)H) = (g 1 g 2) = (g 1) (g 2) = (g 1 H) (g 2 H).
Т 3. Гомоморфный образ группы изоморфен факторгруппе по ядру этого гомоморфизма. Дано: : G 1 G 2; – гомоморфизм, H = Ker . Доказать: G 1/H G 2. Доказательство: Рассмотрим отображение : G 1/H G 2 такое, что g H G 1/H (g H) = (g); g G 1; (g) G 2. Покажем, что – изоморфизм. 1. Взаимная однозначность. Пусть g 1 H = g 2 H (g 2 -1 g 1)H = H g 2 -1 g 1 H, т. е. g 2 -1 g 1 Ker (g 2 -1 g 1) = e' G 2. Т. к. – гомоморфизм, (g 2 -1) (g 1) = e' или ( (g 2))-1 (g 1) = e' (g 1) = (g 2) (g 1 H) = (g 2 H). Обратно, пусть (g 1 H) = (g 2 H), или (g 1) = (g 2), ( (g 2))-1 (g 1) = e' G 2 (g 2 -1 g 1) = e'. Тогда g 2 -1 g 1 Ker = H или (g 2 -1 g 1)H = H g 1 H = g 2 H. 2. Сохранение операции. (g 1 H g 2 H) = ((g 1 g 2)H) = (g 1 g 2) = (g 1) (g 2) = (g 1 H) (g 2 H).


