ИЗОЭНТРОПИЙНОЕ ТЕЧЕНИЕ Закон сохранения энергии 1 1 1

ИЗОЭНТРОПИЙНОЕ ТЕЧЕНИЕ Закон сохранения энергии: (1. 1) (1. 2) Уравнение изоэнтропийного процесса: Уравнение состояния: Для идеального газа: (1. 3) Введем число , где местная изоэнтропийная скорость звука (1. 4)

продолжение ИЗОЭНТРОПИЙНОЕ ТЕЧЕНИЕ Сечение, в котором число М=1, называется критическим. (1. 5) Скорость звука в критическом сечении ак: (1. 6) Плотность и давление в критическом сечении: (1. 7) (1. 8) Двухатомные газы: Многоатомные газы и перегретый водяной пар при небольших давлениях:

продолжение ИЗОЭНТРОПИЙНОЕ ТЕЧЕНИЕ Безразмерные параметры в газодинамических расчетах - безразмерная скорость - масштаб скорости (1. 9) - безразмерная температура - безразмерная плотность - безразмерное давление Связь безразмерных параметров: (1. 10) (1. 11) (1. 12)

продолжение ИЗОЭНТРОПИЙНОЕ ТЕЧЕНИЕ Связь между изменением живого сечения канала и газодинамическими параметрами изоэнтропийного потока Согласно первому закону термодинамики: С учетом (1. 1): (1. 13) Для изоэнтропийного потока: (1. 14) С учетом уравнения неразрывности: (1. 15) (1. 16)

продолжение ИЗОЭНТРОПИЙНОЕ ТЕЧЕНИЕ Дозвуковые течения Расширяющийся канал Замедление потока Суживающийся канал Разгон потока Сверхзвуковые течения Разгон потока Расширяющийся канал Суживающийся канал Замедление потока Критическое сечение Всегда оказывается минимальным

продолжение ИЗОЭНТРОПИЙНОЕ ТЕЧЕНИЕ - безразмерная плотность тока (1. 17) Уравнение неразрывности: (1. 18) Двухатомные газы: Многоатомные газы и перегретый водяной пар при небольших давлениях: (1. 19)

Пример 1. 1. Рассчитать параметры изоэнтропийного течения воздуха на выходе из сопла, если известны температура и давление торможения перед соплом: Давление в потоке за соплом: Найти также площади минимального и выходного сечений при заданном расходе рабочего тела: Показатель адиабаты k принять равным 1, 4.

Решение 1. 1. (1) Температура на выходе из сопла при изоэнтропийном истечении: Плотность в выходном сечении сопла: Скорость изоэнтропийного истечения: Площадь выходного сечения сопла: Перепад давлений на сопло больше критического: Следовательно сопло имеет форму сопла Лаваля. Площадь минимального сечения сопла:

Решение 1. 1. (2) Пользуемся таблицами газодинамических функций изоэнтропийного течения. По известному отношению давлений: находим из таблиц газодинамических функций безразмерные: скорость температуру плотность тока Плотность изоэнтропийного торможения: Критическая скорость звука: Размерные параметры:

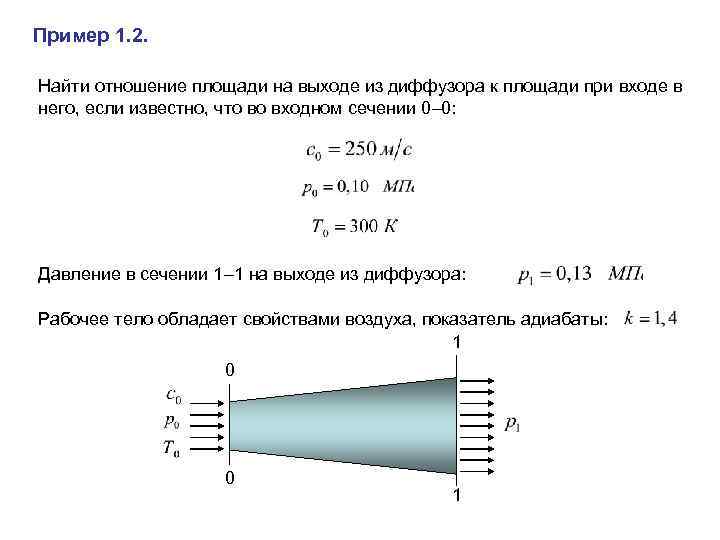Пример 1. 2. Найти отношение площади на выходе из диффузора к площади при входе в него, если известно, что во входном сечении 0 0: Давление в сечении 1 1 на выходе из диффузора: Рабочее тело обладает свойствами воздуха, показатель адиабаты: 1 0 0 1

Решение 1. 2. Скорость звука сечении 0 0 Число М Из таблиц газодинамических функций по Из уравнения (1. 18) следует: найдем:

Пример 1. 3. Найти расход пара, вытекающего из сопла, если известны давление и температура торможения давление за соплом площадь выходного сечения Определить также площадь критического сечения.

Решение 1. 3. По таблицам термодинамических свойств воды и водяного пара для заданных и Зная энтропию и давление в выходном сечении Процесс расширения в is-диаграмме Скорость истечения: Расход пара: Параметры пара в критическом сечении найдем, приближенно приняв

Решение 1. 3. (продолжение) Скорость в критическом сечении Площадь критического сечения Если отказаться от приближенной оценки, то найдем зависимость скорости звука от давления при заданной энтропии. Вычислим частную производную конечными разностями: с использованием минимальных табличных интервалов и взять достаточное число точек, сгладив результат плавной кривой.

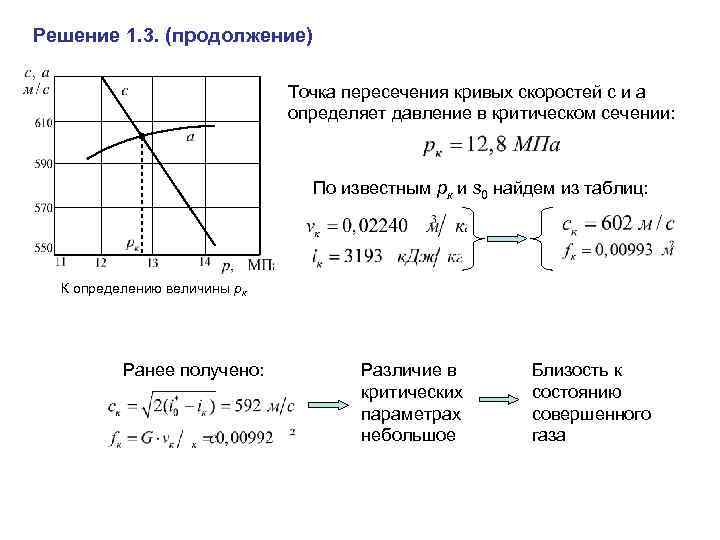Решение 1. 3. (продолжение) Точка пересечения кривых скоростей с и а определяет давление в критическом сечении: По известным рк и s 0 найдем из таблиц: К определению величины рк Ранее получено: Различие в критических параметрах небольшое Близость к состоянию совершенного газа

Решение 1. 3. (выводы) С приближением к линии насыщения, особенно в области критической точки, состояние даже перегретого пара может существенно отклоняться от состояния совершенного газа. Если , то межлопаточные каналы в ступени паровой турбины выполняют суживающимися, допуская расширение потока в косом срезе. Если это отношение больше указанных цифр, то применяют расширяющиеся сопла, но выходное сечение делают приблизительно равным 0, 8 от расчетного с тем, чтобы дальнейшее расширение рабочего тела протекало в косом срезе сопла.

Пример 1. 4. Определить расход пара D в турбине с противодавлением, если начальные параметры пара: Пар перегретый, показатель адиабаты: Степень расширения пара в турбине: . Относительный к. п. д. : Мощность турбины: Задачу решить не пользуясь hs-диаграммой.

Решение 1. 4. Процесс расширения происходит в области перегретого пара. Поэтому располагаемый теплоперепад с достаточной точностью может быть найден по законам идеального газа:

Пример 1. 5. Конденсационная турбина сверхвысоких параметров: имеет промежуточный газовый перегрев пара до температуры: Давление пара перед вторичным перегревом: Потеря давления в тракте промежуточного перегрева: Внутренний к. п. д. части высокого давления: Внутренний к. п. д. части низкого давления: Определить абсолютный к. п. д. цикла Сравнить экономичность этого цикла с экономичностью цикла без промежуточного перегрева, считая, что без перегрева внутренний к. п. д. турбины снизится и составит (в связи с дополнительными потерями в проточной части, вызванными увеличением влажности пара в последних ступенях турбины).

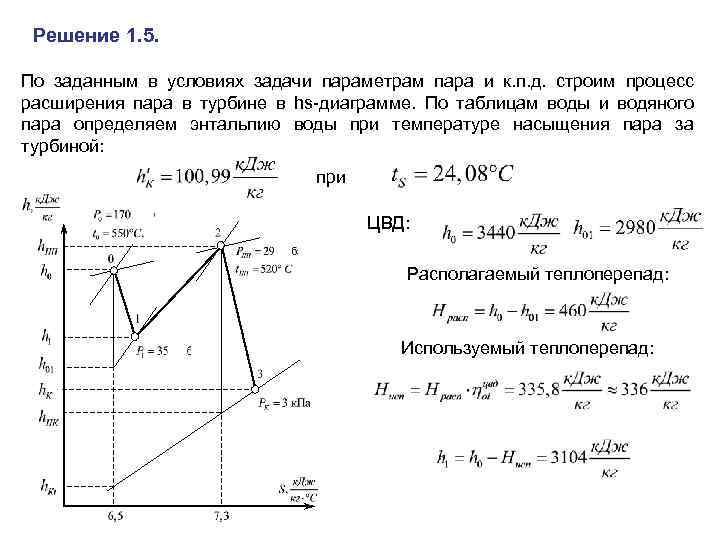Решение 1. 5. По заданным в условиях задачи параметрам пара и к. п. д. строим процесс расширения пара в турбине в hs-диаграмме. По таблицам воды и водяного пара определяем энтальпию воды при температуре насыщения пара за турбиной: при ЦВД: Располагаемый теплоперепад: Используемый теплоперепад:

Решение 1. 5. (продолжение) ЦНД: При адиабатическом расширении пара в ЦВД до давления энтальпия пара понизится до Абсолютный к. п. д. цикла ПТУ с ПП пара составит: Без промежуточного перегрева пара: Выигрыш в экономичности:

ПРОЦЕСС РАСШИРЕНИЯ ПАРА В СТУПЕНИ ТУРБОМАШИНЫ W 1 – скорость, которую имеет пар относительно рабочих лопаток. На выходе из рабочей решетки параметры пара p 2, t 2, h 2, c 2 (скорость относительно рабочих лопаток - W 2).

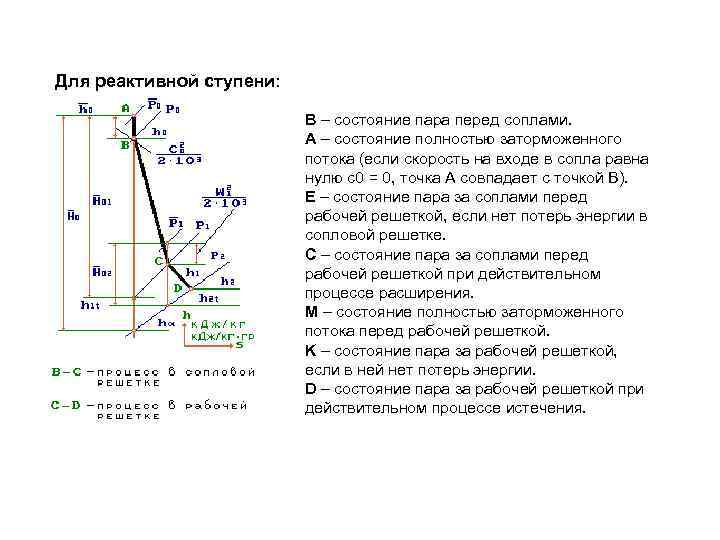Для реактивной ступени: B – состояние пара перед соплами. A – состояние полностью заторможенного потока (если скорость на входе в сопла равна нулю с0 = 0, точка А совпадает с точкой В). E – состояние пара за соплами перед рабочей решеткой, если нет потерь энергии в сопловой решетке. C – состояние пара за соплами перед рабочей решеткой при действительном процессе расширения. M – состояние полностью заторможенного потока перед рабочей решеткой. K – состояние пара за рабочей решеткой, если в ней нет потерь энергии. D – состояние пара за рабочей решеткой при действительном процессе истечения.