Измерение вариации 1 2 3 Абсолютные и относительные

Измерение вариации 1. 2. 3. Абсолютные и относительные показатели вариации Особенности расчёта и свойства показателя дисперсии Правило сложения дисперсий

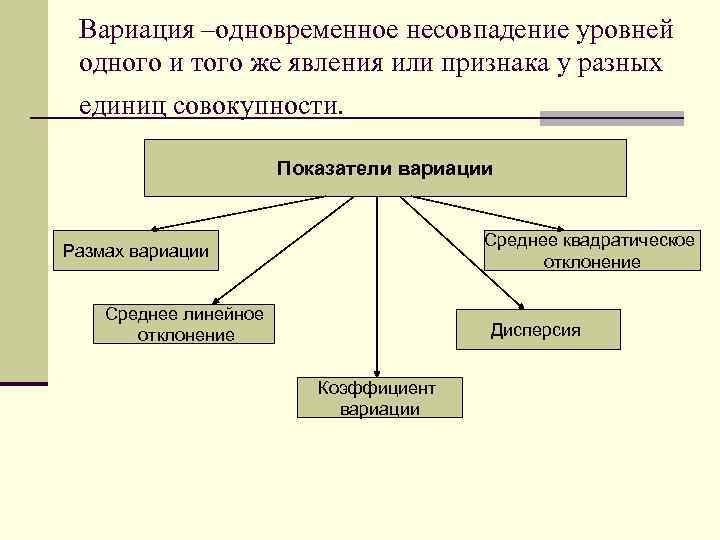
Вариация –одновременное несовпадение уровней одного и того же явления или признака у разных единиц совокупности. Показатели вариации Среднее квадратическое отклонение Размах вариации Среднее линейное отклонение Дисперсия Коэффициент вариации

Размах вариации n Преимущество – простота вычисления n Недостаток – учитывает только крайние значения признака и не отражает существенные черты варьирования n Выход – расчёт среднего квартильного расстояния:

Среднее линейное (абсолютное) отклонение. n Применяется при изучении ритмичности и равномерности производства, равномерности поставок материалов и отгрузки готовой продукции и т. д. n Простое n взвешенное

Среднее квадратическое отклонение n для ранжированного ряда n для интервального ряда

соотношение n служит для изучения структуры вариации: большое значение такого соотношения свидетельствует о наличии слабоварьирующего «ядра» и сильно рассеянного вокруг него окружения в изучаемой совокупности.

Соотношение n служит индикатором «засоренности» совокупности неоднородными с основной массой элементами n Для нормального закона распределения отношение.

Дисперсия n для несгруппированных данных (простая дисперсия) n для сгруппированных (взвешенная дисперсия)

Относительные показатели вариации используются для оценки интенсивности вариации, а также сравнения её величины в разных совокупностях и по разным признакам. n относительный размах вариации (коэффициент осцилляции): n линейный коэффициент вариации: n квадратический коэффициент вариации: n относительное квартильное расстояние:

Оценка и анализ степени интенсивности вариации: n Цель - средняя, рассчитанная для неоднородной совокупности не является её типичной характеристикой n состоит в сравнении наблюдаемой вариации с некоторой обычной ее интенсивностью, принимаемой за норматив. Возможна только для каждого отдельного признака и совокупности определенного состава. n Шкала (условная!) определения степени однородности совокупности в зависимости от υ Коэффициент вариации, % Степень однородности совокупности До 30 высокая 30 -60 средняя 60 и более низкая

Максимально возможное значение показателей вариации. n Среднее линейное отклонение: n Среднее квадратическое отклонение: n Коэффициент вариации:

Момент распределения – средняя арифметическая степеней отклонений индивидуальных значений признака от определённой исходной величины. Дисперсия - Центральный момент второго порядка Формула метода моментов: Центральные моменты более высокого порядка используются: n третьего порядка - для оценки асимметрии (несимметричности разброса данных относительно среднего уровня); n четвёртого – для оценки эксцесса (степени концентрации первичных данных около среднего уровня).

Свойства дисперсии 1. 2. 3. 4. 5. Величина дисперсии не зависит от начала отсчёта признака При увеличении (уменьшении) всех значений признака в С раз показатель дисперсии нового(изменённого) признака будет больше (меньше) в С 2 раз. При небольшом объёме выборочной совокупности расчётная величина дисперсии оказывается смещённой в меньшую сторону по сравнению с генеральной дисперсией Если единицы наблюдения статистически независимы, то для одного и того же признака дисперсия его суммарной величины равна сумме дисперсий признака в отдельных наблюдаемых единицах.

Дисперсия альтернативного признака n w – средняя величина альтернативного показателя (доля или удельный вес)

Правило сложения дисперсий Если первичные данные разделены на k групп, то общая дисперсия признака - межгрупповая дисперсия - средняя из внутригрупповых дисперсий mj - количество объектов наблюдений, включённых в группу j

Расчёт дисперсий mj - количество объектов наблюдений, включённых в группу j среднее значение по группе общее среднее значение признака

• Эмпирический коэффициент детерминации Характеризует силу влияния группировочного (факторного) признака на результативный. Изменяется от 0 до 1 n Эмпирическое корреляционное отношение. Показывает тесноту связи между группировочным и результативным признаком

Качественная оценка тесноты связи по эмпирическому корреляционному отношению (η) Шкала Чеддока Значение η Сила связи 0 -0, 1 отсутствует 0, 1 -0, 3 слабая 0, 3 -0, 5 умеренная 0, 5 -0, 7 -0, 9 -0, 99 заметная тесная весьма тесная 1 функциональная