Арифметические и логические основы ВТ.pptx
- Количество слайдов: 7

Измерение информации В вычислительной технике бит (binary digit) – ячейка памяти, необходимая для хранения одного из двух знаков « 0» или « 1» . 1 Килобайт (Кбайт) 1 Мегабайт (Мбайт) 1 Гигабайт (Гбайт) 1 Терабайт (Тбайт) = 1024 байт = 1024 Кбайт = 1024 Мбайт = 1024 Гбайт =210 байт =220 байт =230 байт =240 байт

Арифметические основы компьютера В вычислительной технике используется двоичная система счисления, так как: • Для ее реализации нужны технические устройства с двумя устойчивыми состояниями; • Представление информации посредством только двух состояний надежно и помехоустойчиво; • Возможно применение аппарата булевой алгебры для выполнения логических преобразований информации. Двоичная система счисления является позиционной. Основание позиционной системы счисления – это количество различных цифр, используемых для изображения чисел в данной системе счисления. В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен. Число N в позиционной системе счисления с основанием q представляется в виде Где m – количество разрядов (цифр) рассматриваемого числа; k – разряд цифры; ak - числовой знак (цифра), причем 0 ≤ ak ≤ q-1 Например, число 103 представляется в десятичной системе счисления в виде: 103 = 1· 102 + 0· 101 + 3· 100

Как перевести целое число из десятичной системы счисления в любую другую позиционную систему счисления Для перевода целого десятичного числа N в систему счисления с основанием q следует разделить N на q с остатком. Затем неполное частное, полученное от этого деления, нужно снова разделить на q с остатком и т. д. , пока последнее полученное неполное частное не станет равным нулю. Число N в системе счисления с основанием q представится в виде последовательности полученных остатков деления, записанных одной q-ичной цифрой в порядке, обратном порядку их получения. Пример. Представим число 75 в двоичной, восьмеричной и шестнадцатеричной системах счисления.

Как перевести правильную десятичную дробь в любую другую позиционную систему счисления Для перевода правильной десятичной дроби F в систему счисления с основанием q следует F умножить на q, затем дробную часть полученного произведения снова умножить на q и т. д. до тех пор, пока дробная часть очередного произведения не станет равной нулю, либо не будет достигнута требуемая точность изображения числа F в q-ичной системе счисления. Представлением дробной части числа F в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных одной q-ичной цифрой. Пример. Перевести число 0, 625 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную. 0, 625 × 2 1, 25 × 2 0, 5 × 2 1 0 0, 62510 = 0, 1012 0, 625 × 8 5, 0 0, 62510 = 0, 58 0, 625 × 16 A 16=10, 0 0, 62510 = 0, A 16
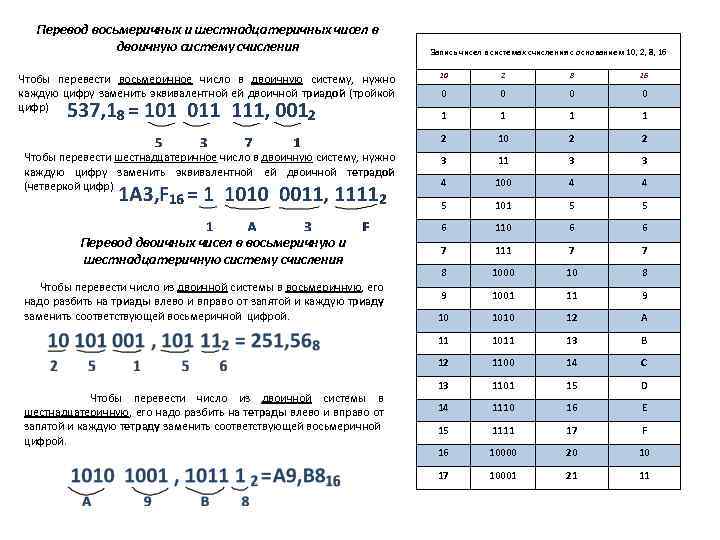
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления Запись чисел в системах счисления с основанием 10, 2, 8, 16 Чтобы перевести число из двоичной системы в шестнадцатеричную, его надо разбить на тетрады влево и вправо от запятой и каждую тетраду заменить соответствующей восьмеричной цифрой. 16 0 0 1 1 10 2 2 3 11 3 3 4 100 4 4 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 A 1011 13 B 12 Чтобы перевести число из двоичной системы в восьмеричную, его надо разбить на триады влево и вправо от запятой и каждую триаду заменить соответствующей восьмеричной цифрой. 8 11 Перевод двоичных чисел в восьмеричную и шестнадцатеричную систему счисления 2 5 Чтобы перевести шестнадцатеричное число в двоичную систему, нужно каждую цифру заменить эквивалентной ей двоичной тетрадой (четверкой цифр) 10 2 Чтобы перевести восьмеричное число в двоичную систему, нужно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F 16 10000 20 10 17 10001 21 11

Логические основы компьютера • Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. • Для описания того, как функционируют аппаратные средства компьютера очень удобен математический аппарат алгебры логики. Значения 0 и 1 представляют собой состояние ячейки памяти объемом в 1 бит или наличие/отсутствие напряжения в электрической схеме. • Алгебра логики позволяет строить сложные электронные узлы, элементы которых работают согласно этой математической теории. • Еще одно практическое применение булевой алгебры - в логических построениях в математике. В этом случае булевы значения - это "ложь" и "истина". Они определяют истинность или ложность некоторого высказывания. Под высказываниями понимаются математические формулы.
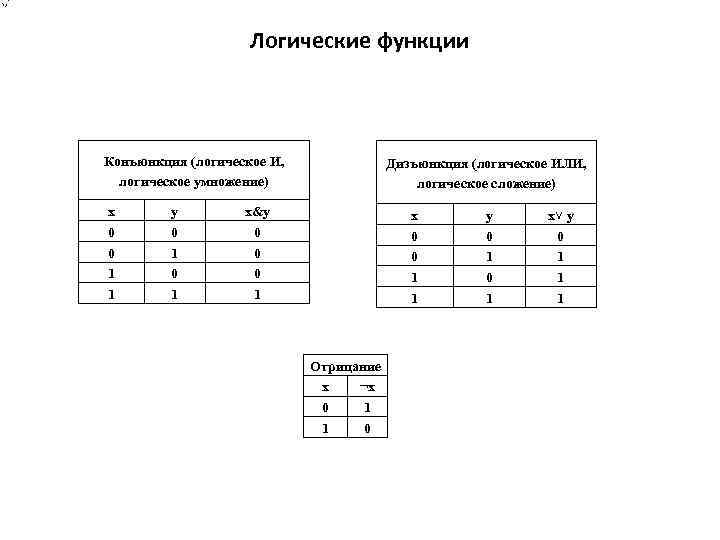
Логические функции Конъюнкция (логическое И, логическое умножение) x 0 0 1 1 y 0 1 Дизъюнкция (логическое ИЛИ, логическое сложение) x&y 0 0 0 1 x 0 0 1 1 Отрицание x ¬x 0 1 1 0 y 0 1 x˅ y 0 1 1 1
Арифметические и логические основы ВТ.pptx