Изгибаемые ж. б.

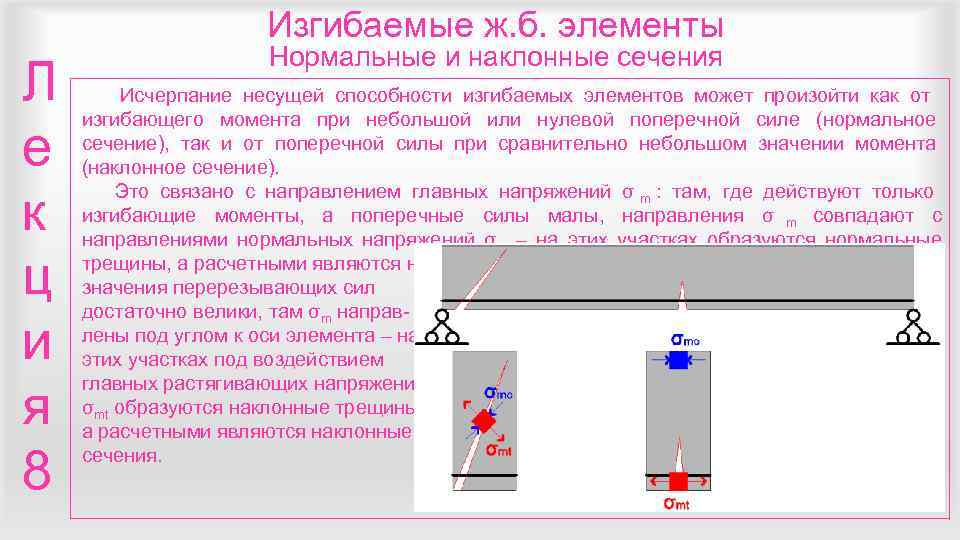
Изгибаемые ж. б. элементы Нормальные и наклонные сечения Л Исчерпание несущей способности изгибаемых элементов может произойти как от изгибающего момента при небольшой или нулевой поперечной силе (нормальное е сечение), так и от поперечной силы при сравнительно небольшом значении момента (наклонное сечение). Это связано с направлением главных напряжений σ m : там, где действуют только к изгибающие моменты, а поперечные силы малы, направления σ m совпадают с направлениями нормальных напряжений σ х – на этих участках образуются нормальные ц трещины, а расчетными являются нормальные сечения. Там, где значения перерезывающих сил достаточно велики, там σm направ- и лены под углом к оси элемента – на этих участках под воздействием главных растягивающих напряжений я σmt образуются наклонные трещины, а расчетными являются наклонные 8 сечения.

Нормальные сечения Граничная высота сжатой зоны. Л Это такая высота (абсолютная х. R или относительная ξR = х. R/h 0), при которой в предельной по прочности стадии, т. е. в 3 -ей стадии непосредственно перед разрушением, напряжения е в сжатом бетоне σ b и в растянутой арматуре σ s одновременно достигают своих предельных значений (расчетных сопротивлений), т. е. σ b = R b и σ s = R s - т акое сечени называют нормально армированным. к Если армирование уменьшить, то высота сжатой зоны тоже уменьшится и станет меньше граничной, т. е. х< х. R – такое сечение называют слабо армированным. ц Если армирование увеличить, то окажется что х>х R - такое сечение называется переармированным. Следует иметь в виду, что понятия нормально-, слабо- и переармированные сечения и условны, применяются только в сугубо практической деятельности и отсутствуют в Нормах. я 8

Нормальные сечения Слабо-, нормально- и переармированные сечения. Л По условиям статики, в предельной стадии усилие в сжатой зоне бетона равно усилию в растянутой арматуре, т. е. Nb = Ns или Rb ∙Ab = Rs ∙As или Rb∙ b∙x= Rs∙As. е Очевидно, что с увеличением As увеличивается и Ab, следовательно увеличивается x. Слабо армированное сечение при х< х R деформации в арматуре достигли начала площадки текучести (ε s = ε pl ), а в бетоне не достигли предельной сжимаемости (ε b <ε bu ). На к первый взгляд прочность бетона недоиспользуется и сечение работает нерационально. Однако у арматуры есть площадка текучести, а значит, по мере текучести стали, когда деформации в ней увеличиваются с ε pl до ε pl 1 , увеличиваются и деформации бетона, ц достигая в итоге εbu. Нормально армированное сечение при х=х R работает наиболее рационально: ε b и ε s и одновременно достигают значений ε b u и ε pl , а напряжения - значений R b и соответственно. В переармированном сечении при х>х R деформации бетона достигают ε bu , а я деформации арматуры не достигают εpl , т. е. прочность бетона Rb используется полностью, а прочность арматуры Rs – нет. Слабо- и нормально армированные сечения 8 имеют общий признак – в них бетон и арматура полностью используют свою прочность, поэтому принцип их расчета

Нормальные сечения Расчет прочности прямоугольных сечений с одиночной арматурой. Л По условиям статики, в предельной стадии усилие в сжатой зоне бетона равно усилию в е растянутой арматуре Rb∙b∙x= Rs∙As. 1. Исходя из этого равенства определяют высоту сжатой зоны бетона х= Rs∙As/ Rb∙b; 2. По найденному значению х определяют относительную высоту сжатой зоны ξ =х /h 0 , и к сравнивают с предельным значением ξ R ( зависит от класса арматуры и берется из специальных таблиц). Если ξ≤ ξR - то случай 1, если ξ> ξR - то случай 2. ц 3. Если ξ≤ ξR то x≤x. R и растянутая арматура S работает с полной отдачей, а усилия в ней составляют R s ∙ A s. Поскольку фактическая криволинейная эпюра заменена условно прямоугольной, то равнодействующая и 1. сжимающих сил в бетоне Rb∙b∙x, приложенной в центре тяжести сжатой зоны, 2. т. е. посредине высоты х. Плечо внутренней я 3. 4. пары сил составляет (h 0 -0. 5 x). Таким образом несущая способность сечения 8 5. составляет M=Rb∙b∙x∙(h 0 -0. 5 x) или М= Rs∙As∙ (h 0 -0. 5 x); 6. Если ξ> ξR , то расчет производят аналогично 7. случаю 1, но при x=x. R= ξR∙h 0; т. е. M=Rb∙b∙x. R∙(h 0 -0. 5 x. R)
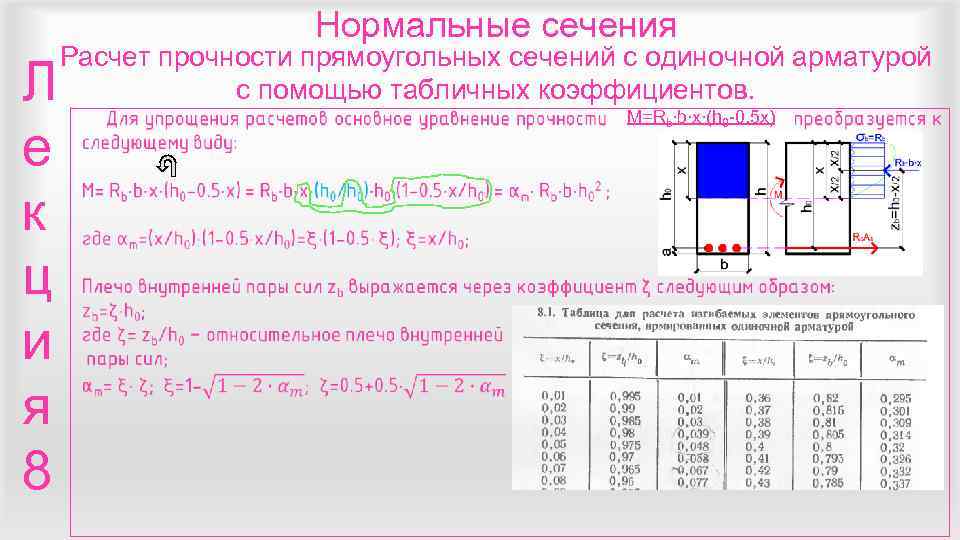
Нормальные сечения Расчет прочности прямоугольных сечений с одиночной арматурой Л с помощью табличных коэффициентов. M=Rb∙b∙x∙(h 0 -0. 5 x) е к ц и я 8

Нормальные сечения Расчет прочности прямоугольных сечений с двойной арматурой Л е к ц и я 8

Нормальные сечения Конструктивные требования Л е к ц и я 8

Нормальные сечения Конструктивные требования Л Схема расположения арматуры в горизонтальном ряду е a 3 принимается: Ø не менее 20 мм при h≥ 250 мм; к Ø не менее 15 мм при h<250 мм; Ø не менее d ц aw принимается: и Ø не менее 15 мм при h≥ 250 мм; Ø не менее 10 мм при h<250 мм; я 8
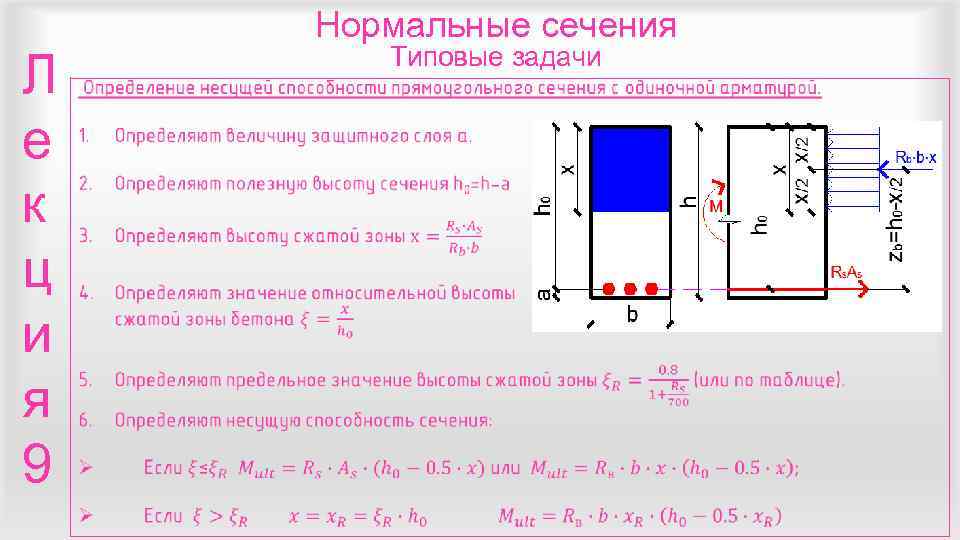
Нормальные сечения Типовые задачи Л е к ц и я 9
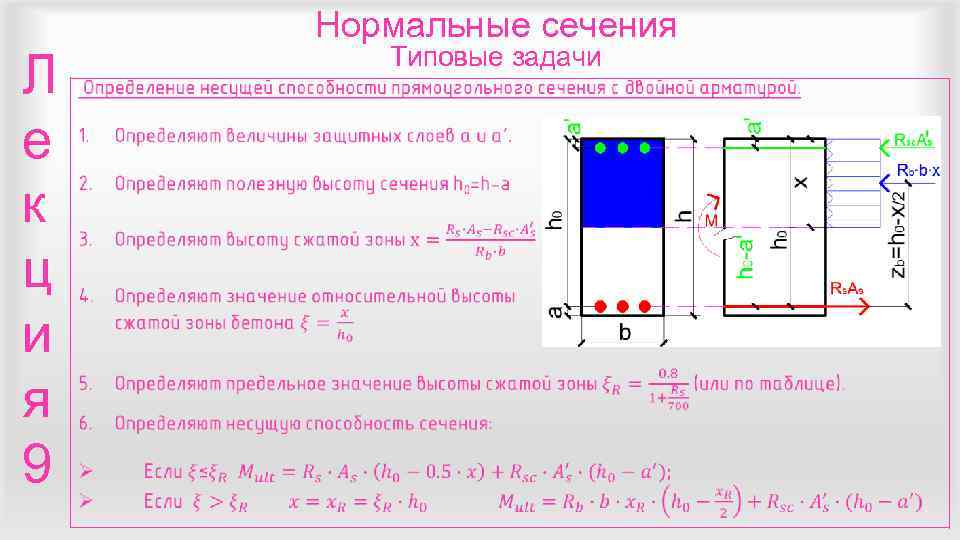
Нормальные сечения Типовые задачи Л е к ц и я 9

Нормальные сечения Типовые задачи Л е к ц и я 9
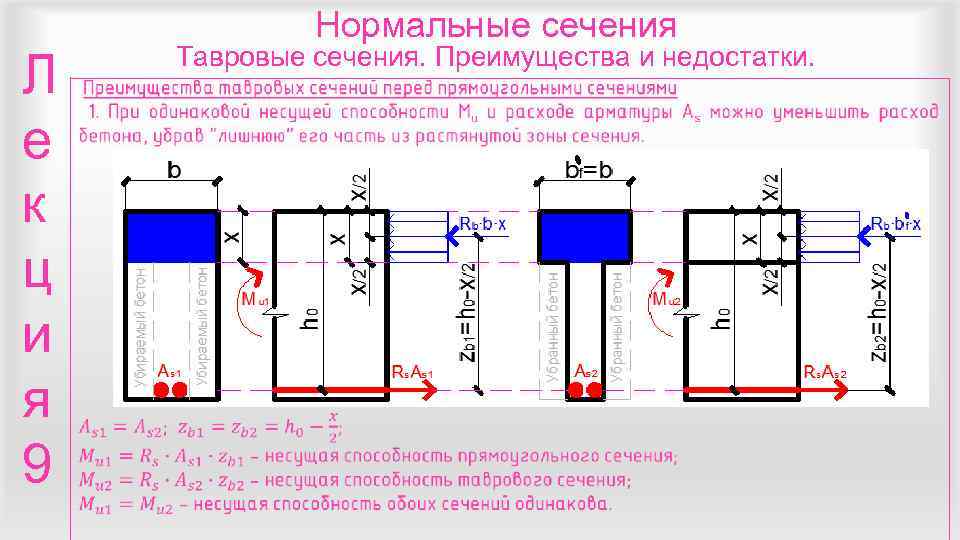
Нормальные сечения Тавровые сечения. Преимущества и недостатки. Л е к ц и я 9
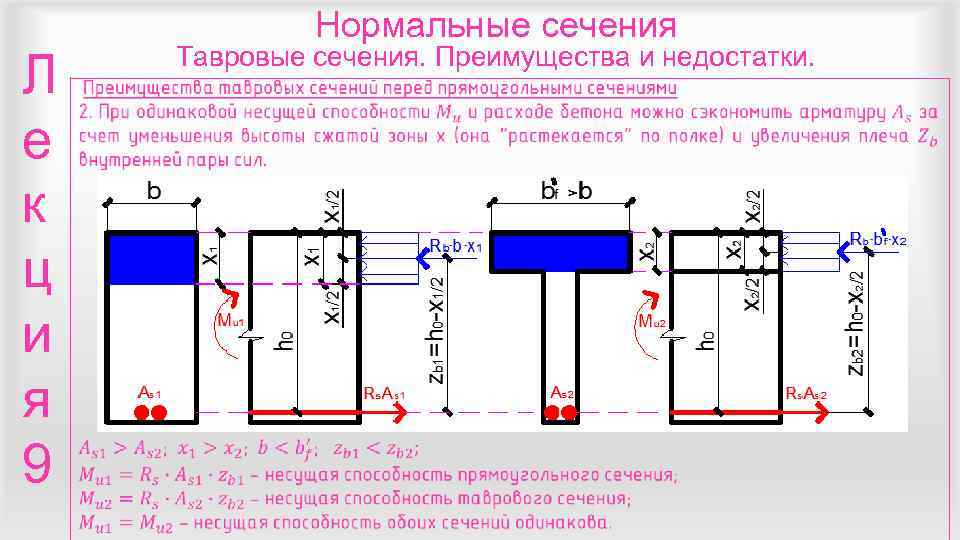
Нормальные сечения Тавровые сечения. Преимущества и недостатки. Л е к ц и я 9
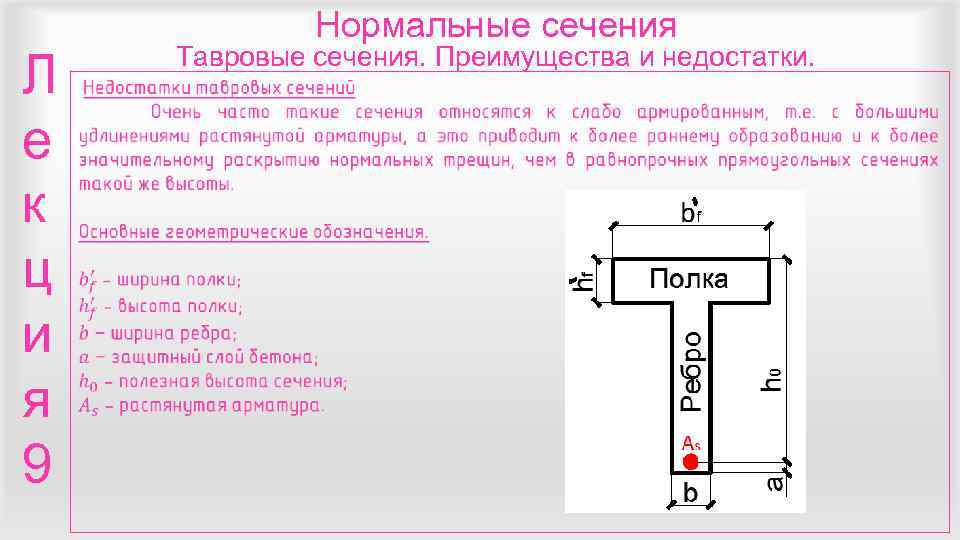
Нормальные сечения Тавровые сечения. Преимущества и недостатки. Л е к ц и я 9
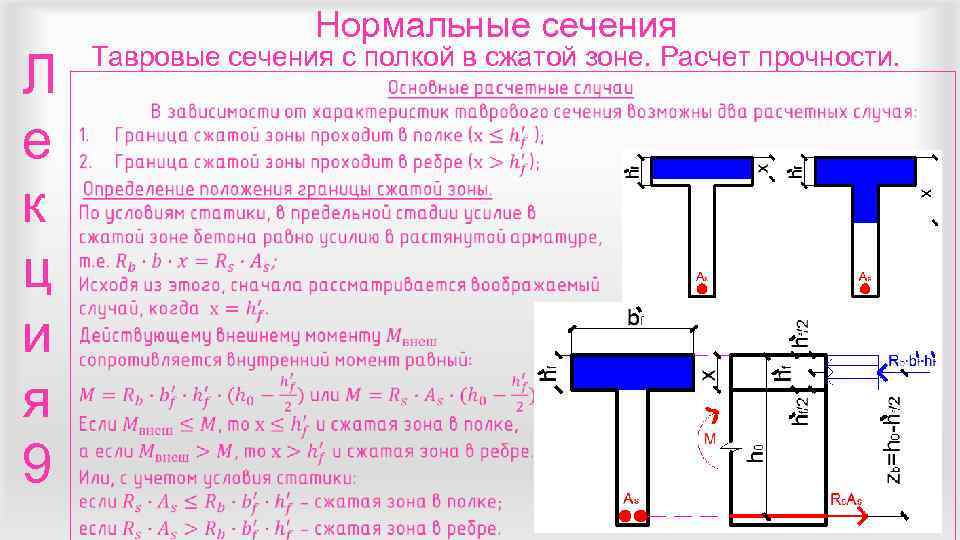
Нормальные сечения Тавровые сечения с полкой в сжатой зоне. Расчет прочности. Л е к ц и я 9

Нормальные сечения Л е к ц и я 9

Нормальные сечения Л е к ц и я 9

Нормальные сечения Подбор арматуры в тавровом сечении с полкой в сжатой зоне Л е к ц и я 9

