ИЗБРАННЫЕ ЛЕКЦИИ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ Лекция 1. Числовые функции и их свойства
Основным предметом исследования в математическом анализе, а, следовательно, и основным его понятием является понятие функции. Пусть Х, Y – числовые множества. Определение. Закон, по которому каждому числу х из Х ставит в соответствие одно вполне определенное число у из Y, называется числовой или вещественной функцией, заданной на Х. Записывают y = f (x). Переменную x, пробегающую множество Х, называют аргументом функции. Множество Х называют областью задания или областью определения функции f и обозначают D(f). С каждой функцией связано множество Y= {f(x)|x Х}. Его называют областью значений (или множеством значений) функции f и обозначают Е(f). Чтобы задать функцию f, надо указать её область задания Х и правило, по которому каждому x Х сопоставляется число y. Обычно это правило даётся в виде некоторого выражения, показывающего, какие операции нужно выполнить над х, чтобы получить f(x).
График функции Определение. Графиком функции f называют множество всех точек (х; у) координатной плоскости, где у= f(x), а х «пробегает» всю область определения функции f. Заданная на координатной плоскости линия является графиком какой-либо функции, если каждая прямая, параллельная оси Оу, пересекает ее не более чем в одной точке.
Чётные, нечётные функции Определение. Функция f называется чётной, если для любого х из её области определения f(–x) = f(x). Определение. Функция f называется нечётной, если для любого х из её области определения f(–x) = – f(x). При построении графиков чётных и нечётных функций будем пользоваться следующими известными из курса алгебры свойствами: 1. График чётной функции симметричен относительно оси ординат. 2. График нечётной функции симметричен относительно начала координат. Из этих двух правил вытекает следующее: при построении графика чётной или нечётной функции достаточно построить его часть для неотрицательных х, а затем отразить полученный график относительно оси ординат (в случае чётной функции) или начала координат (в случае нечётной функции).
Нули функции. Интервалы знакопостоянства функции Определение. Нулём (или корнем) функции f(x) называется такое значение аргумента х, при котором функция обращается в нуль. Графически нули функции суть точки пересечения её графика с осью Ох. Определение. Интервалы знакопостоянства функции — это интервалы, в которых функция только положительна или только отрицательна.
Периодичность Определение. Функцию f называют периодической с периодом Т 0, если для любого х из области определения значения этой функции в точках х, х – Т, х + Т равны, т. е. f(х +Т) = f(x) = f(х – Т). Наименьший положительный период функций y= sin x и y = cos x равен 2. Наименьший положительный период функций y = tg x и y = ctg x равен .
Монотонность функции, интервалы монотонности. Экстремумы функции Определение. Функция f возрастает на множестве Х, если для любых х1 и х2 из множества Х, таких, что х2 > х1, выполнено неравенство f(х2) > f(х1). Определение. Функция f убывает на множестве Х, если для любых х1 и х2 из множества Х, таких, что х2 > х1, выполнено неравенство f(х2) < f(х1). При исследовании поведения функции вблизи некоторой точки удобно пользоваться понятием окрестности. Окрестностью точки х = х0 называется любой интервал, содержащий эту точку.
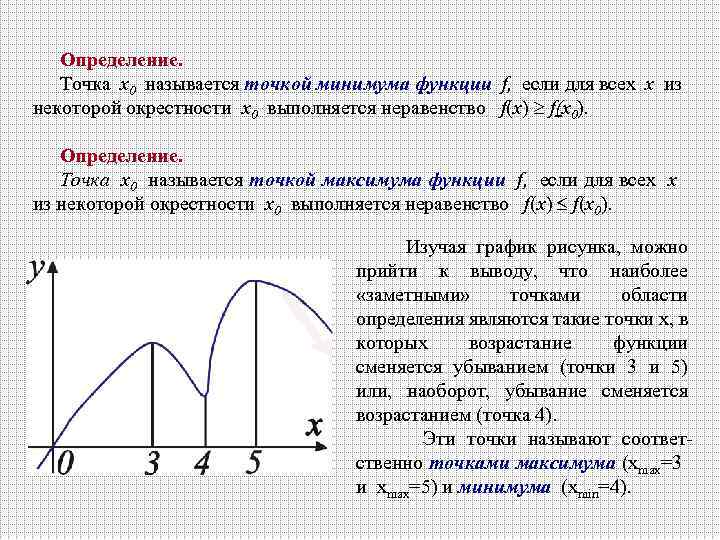
Определение. Точка х0 называется точкой минимума функции f, если для всех х из некоторой окрестности х0 выполняется неравенство f(x) f(х0). Определение. Точка х0 называется точкой максимума функции f, если для всех х из некоторой окрестности х0 выполняется неравенство f(x) f(х0). Изучая график рисунка, можно прийти к выводу, что наиболее «заметными» точками области определения являются такие точки х, в которых возрастание функции сменяется убыванием (точки 3 и 5) или, наоборот, убывание сменяется возрастанием (точка 4). Эти точки называют соответственно точками максимума (хmax=3 и хmax=5) и минимума (хmin=4).
Автор: М. М. Цвиль, кандидат физико-математических наук, доцент кафедры информационных таможенных технологий и информатики
Скачать презентацию ИЗБРАННЫЕ ЛЕКЦИИ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ Лекция 1 Числовые
математика лекция (1).ppt