Lectures 1_2-11.ppt
- Количество слайдов: 79

«Избранные главы неорганического материаловедения» Лектор: проф. Кауль Андрей Рафаилович Ассистент: Бурова Лидия Игоревна • 36 часов (2 часа в неделю) • Домашние задания (!!) • 2 контрольных работы (!) • Проверочные работы на лекциях • Экзамен… 1

Литература к курсу «Избранные главы неорганического материаловедения» 1. Л. Ван-Флек « Теоретическое и прикладное материаловедение» , Мир, 1985. 2. Ф. Райнз «Диаграммы фазового равновесия в металлургии» , Металлургиздат, 1961. 3. А. Вест « Химия твердого тела» , Мир, 1988, т. 1, 2. 4. И. И. Новиков « Теория термической обработки металлов» , Металлургиздат, 1974. 5. Д. Дью-Хьюз, «Металлы, керамика, полимеры» , Атомиздат, 1979. 6. Третьяков Ю. Д. , Путляев В. И. , «Введение в химию твердофазных материалов» , 2006. 7. Кнотько А. В. , Пресняков И. А. , Третьяков Ю. Д. , «Химия твердого тела» , 2006. 8. Г. Готтштайн «Физико-химические основы материаловедения» , 2009. 2

Направленность курса: изучение наиболее общих закономерностей материаловедения, явлений и процессов, иллюстрируемых на примерах различных групп материалов. 3
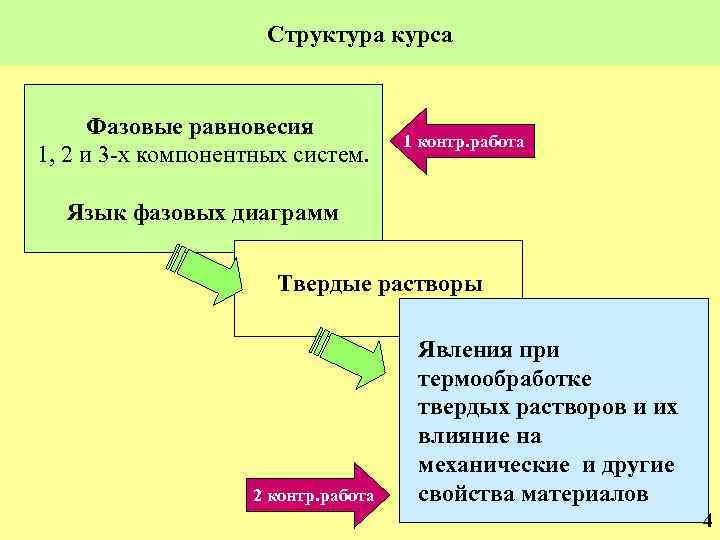
Структура курса Фазовые равновесия 1, 2 и 3 -х компонентных систем. 1 контр. работа Язык фазовых диаграмм Твердые растворы 2 контр. работа Явления при термообработке твердых растворов и их влияние на механические и другие свойства материалов 4

Материал – вещество, отвечающее тем или иным требованиям его применения 5

Материалы определяют уровень цивилизаций Историческая периодизация: Каменный век Бронзовый век Железный век 6

Важнейшие материалы, изменившие жизнь человечества Строительство: Глина – Дерево – Камень – Бетон 7

Важнейшие материалы, изменившие жизнь человечества Военное дело: Порох 8
Важнейшие материалы, изменившие жизнь человечества Передача информации: Глина – Папирус – Бумага Кремний 9
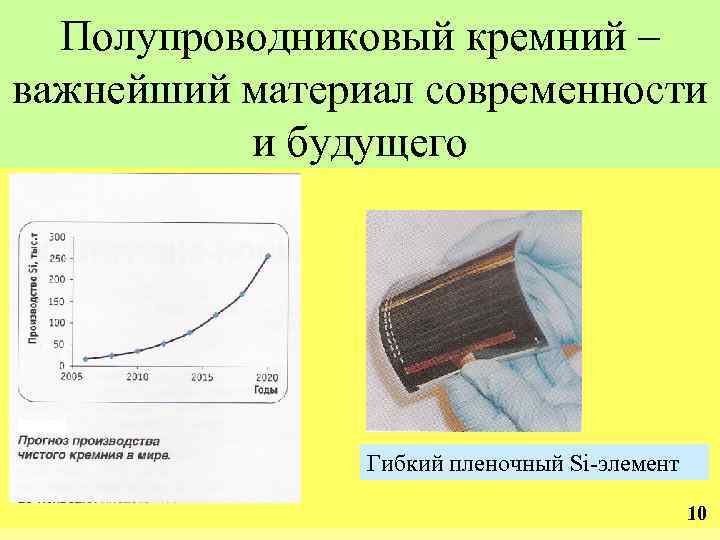
Полупроводниковый кремний – важнейший материал современности и будущего Гибкий пленочный Si-элемент 10

Разработка новых материалов – одна из главных целей деятельности химиков 11

Особенность современного материаловедения – разработка материалов для решения конкретной задачи 12
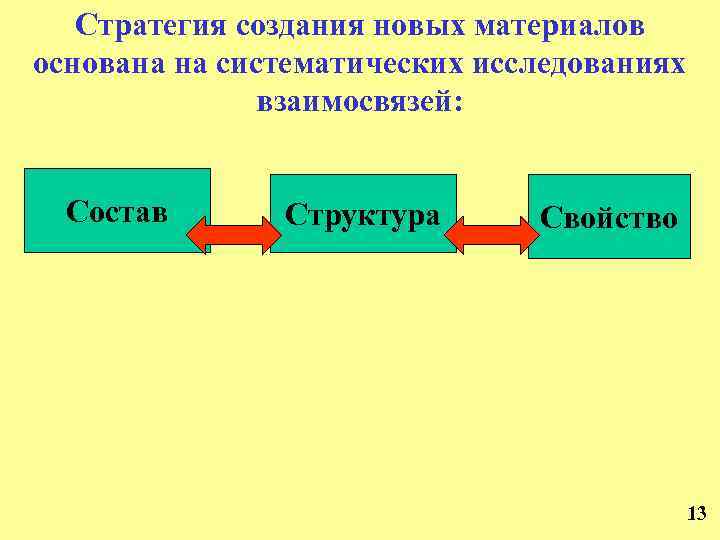
Стратегия создания новых материалов основана на систематических исследованиях взаимосвязей: Состав Структура Свойство 13
Стратегия создания новых материалов основана на систематических исследованиях взаимосвязей: Состав Структура Свойство «Подход технолога» 14
Стратегия создания новых материалов основана на систематических исследованиях взаимосвязей: Состав Структура Свойство «Подход химикасинтетика» 15
Стратегия создания новых материалов основана на систематических исследованиях взаимосвязей: Состав Структура Свойство «Подход физика» 16

Современное понимание термина «состав» • Элементный состав Zn, O • Стехиометрия Zn. O • Нестехиометрия Zn. O 1 -x (изоляторп/проводник) • Однородность состава • Тип и концентрация примесей (Li, N) –p; (Ga, Al)-n • Распределение примесей • Фазовый состав 1 фаза, 2 фазы ? 17

Что понимают под термином «структура» ? • Атомная и электронная структура • Кристаллическая структура • Структура дефектов • Наноструктура • Мезоструктура • Микроструктура • Структура поверхности 18
Свойства материалов • Химические (реакционная способность, каталитические св-ва). • Физические Механические Электрические Магнитные Оптические Радиационные и их комбинации • Биологические ( биосовместимость и т. д. ) • Технологические (прессуемость, спекаемость и т. д. ) 19
Свойства Структурнонечувствительные (фундаментальные) Структурночувствительные 20

Структурно-нечувствительные свойства • теплоемкость • упругость пара • электродвижущая сила • коэффициент теплового расширения • критическая температура сверхпроводников • ……. . 21

Структурно-чувствительные свойства • предел прочности • теплопроводность • электропроводность • скорость распространения звука • магнитная индукция • сегнетоэлектрическая поляризация • критический ток сверхпроводников • ……. . 22

Электропроводность – пример структурно-чувствительного свойства. Электропроводность зависит не только от - фундаментальных свойств составляющих фаз: - типа носителей заряда (электроны, ионы), - анизотропии структуры, - термодинамических параметров системы (Т, Р, Х), но также от факторов микроструктуры: - относительной плотности (пористости) - среднего размера кристаллитов - текстуры. 23
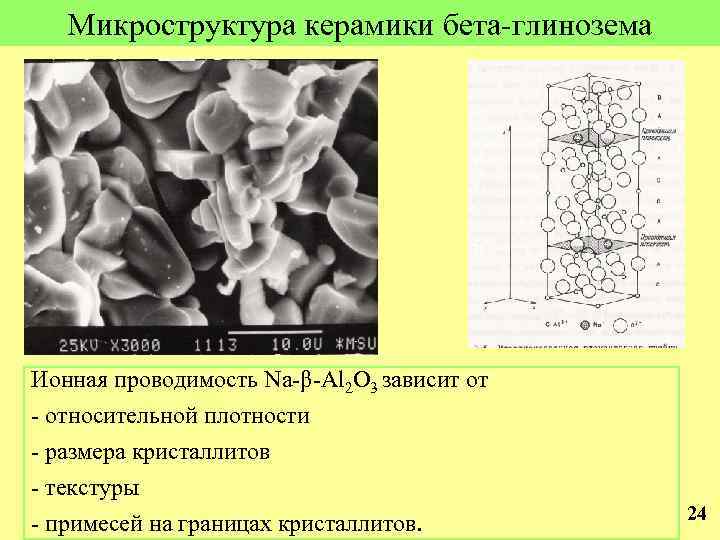
Микроструктура керамики бета-глинозема Ионная проводимость Na-β-Al 2 O 3 зависит от - относительной плотности - размера кристаллитов - текстуры - примесей на границах кристаллитов. 24
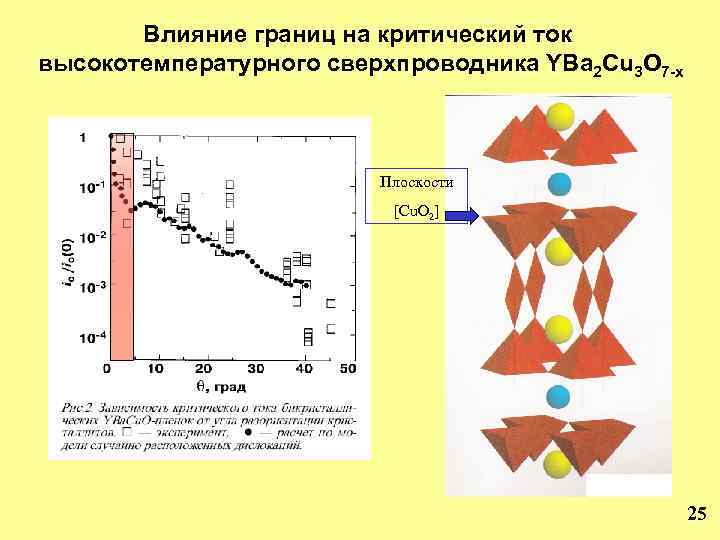
Влияние границ на критический ток высокотемпературного сверхпроводника YBa 2 Cu 3 O 7 -x Плоскости [Cu. O 2] 25

Микроструктура керамики сверхпроводника YBa 2 Cu 3 O 7 -x Тс ~ 92 К Jc: в керамике ~ 102 -104 А/см 2 в монокристаллах ~ 104 А/см 2 в тонких пленках >106 А/см 2 Jc резко зависит от угла разориентации зерен и выделений на границах между ними. 26

Морфология поверхности пленки YBа 2 Cu 3 O 7 -х/Mg. O/RABi. TS Зерна а-ориентированной фазы YBa. Cu. O Микропоры 27

Микроструктура пленки YBa 2 Cu 3 O 7 c Ba. Zr. O 3 YBa 2 Cu 3 O 7+4%мол. Ba. Zr. O 3 c b Просвечивающая электронная микроскопия 30 нм Подтвержден колончатый характер роста включений Ba. Zr. O 3. Включения имеют размер около 10 нм и равномерно распределены в матрице 28
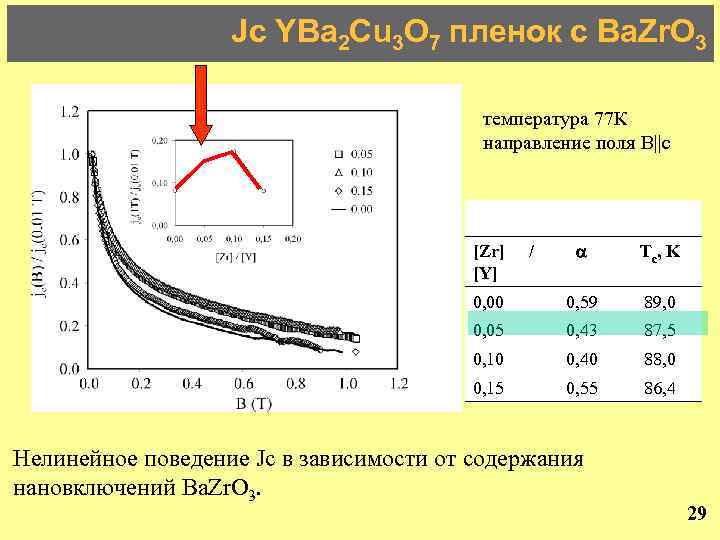
Jc YBa 2 Cu 3 O 7 пленок с Ba. Zr. O 3 температура 77 К направление поля В||с Tc, K 0, 00 0, 59 89, 0 0, 05 0, 43 87, 5 0, 10 0, 40 88, 0 0, 15 0, 55 86, 4 [Zr] [Y] / Нелинейное поведение Jc в зависимости от содержания нановключений Ba. Zr. O 3. 29

Наноматериалы: структурная чувствительность свойств наноматериалов определяется не только наличием границ зерен, но и изменением фундаментальных характеристик веществ при изменении размера частиц до величины порядка нескольких параметров элементарных ячеек. 30
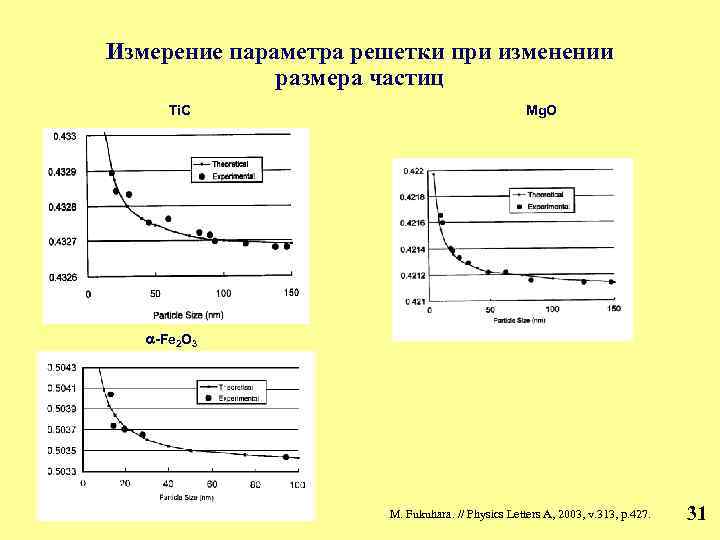
Измерение параметра решетки при изменении размера частиц Ti. C Mg. O -Fe 2 O 3 M. Fukuhara. // Physics Letters A, 2003, v. 313, p. 427. 31
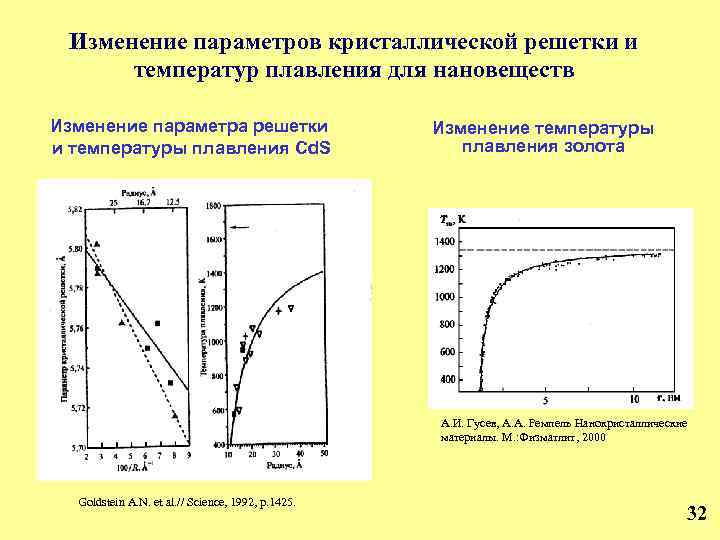
Изменение параметров кристаллической решетки и температур плавления для нановеществ Изменение параметра решетки и температуры плавления Cd. S Изменение температуры плавления золота А. И. Гусев, А. А. Ремпель Нанокристаллические материалы. М. : Физматлит, 2000 Goldstein A. N. et al. // Science, 1992, p. 1425. 32

К структурно-чувствuтельным свойствам (и процессам) относятся те физические свойства материалов (и процессы), которые связаны с перемещением атомов, носителей электрических зарядов (электронов, ионов), фотонов и фононов, дислокаций, границ зерен, доменных стенок на расстояния больше межатомных. Примеры структурно- чувствительных процессов: пластическая деформация, диффузия, старение, спекание, электропроводностъ, теплопроводностъ, намагничивание, распространение звука и др. 33

Избранные главы неорганического материаловедения Лекция 2 1. Роль фазовых диаграмм в материаловедении 2. Определения: системы, фазы, компоненты 3. Химический потенциал 4. Правило фаз 5. Однокомпонентные системы 6. Двухкомпонентные системы • • Классификация превращений в 2 -х компонентных системах Моновариантные процессы
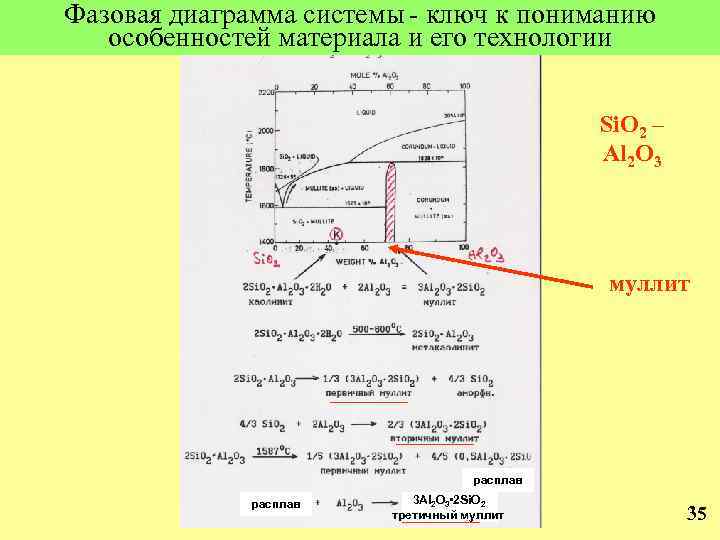
Фазовая диаграмма системы - ключ к пониманию особенностей материала и его технологии Si. O 2 – Al 2 O 3 муллит расплав 3 Al 2 O 3 • 2 Si. O 2 третичный муллит 35

Физико-химическая система – совокупность выделенных из окружающей среды материальных объектов, между которыми возможен обмен энергией и веществом. 36

Гетерогенная система – физико -химическая система, содержащая поверхности раздела, на которых происходит скачкообразное изменение какого-либо свойства системы. 37

Фаза – совокупность идентичных (по составу и свойствам) гомогенных частей гетерогенной системы. 38

Компоненты – индивидуальные вещества, составляющие систему. Число компонентов – минимальное число индивидуальных веществ , из которых может быть составлена любая фаза системы. 39
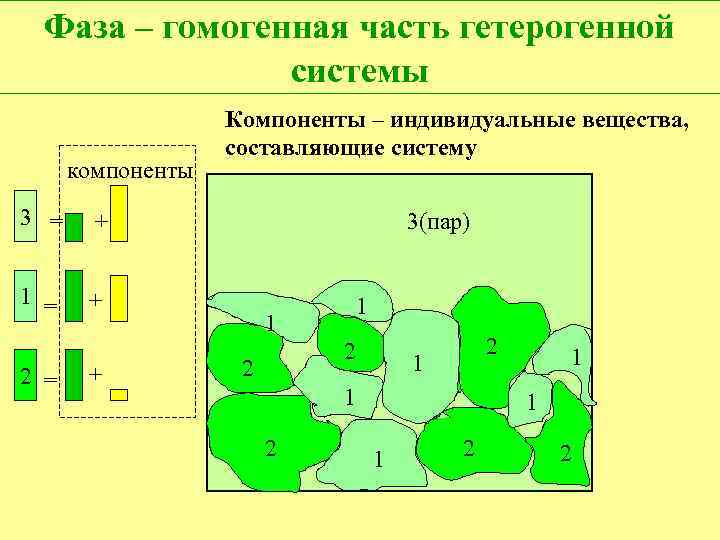
Фаза – гомогенная часть гетерогенной системы компоненты 3 = + 1 = Компоненты – индивидуальные вещества, составляющие систему + 2 = + 3(пар) 1 1 2 2 2 1 1 1 2 2

Примеры: а) “конденсированная” система Al 2 O 3 – Ti. O 2 2 -хкомпонентная б) система Al 2 O 3 – Ti. O 2 при высокой температуре и низком Ро 2 3 -хкомпонентная 41

Определение химического потенциала компонента μ j = μ jo + a j = γ jc j RTlnaj

Химическое равновесие гетерогенной системы достигается тогда, когда химические потенциалы каждого из компонентов равны во всех фазах системы
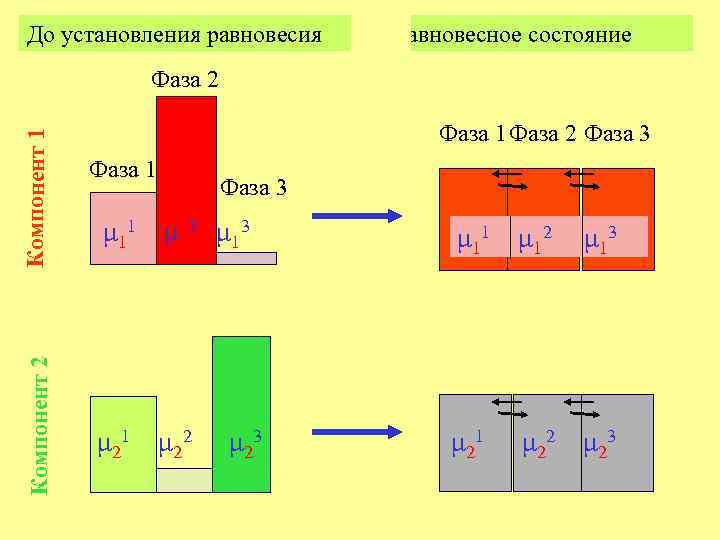
До установления равновесия Равновесное состояние Компонент 2 Компонент 1 Фаза 2 Фаза 1 Фаза 2 Фаза 3 Фаза 1 Фаза 3 μ 11 μ 12 μ 13 3 μ 21 μ 22 μ 2μ 23 μ 11 μ 12 μ 13 μ 21 μ 222 μ 2323 μ 21 μ 2 μ

При равновесии k фаз в n- компонентной системе: 1= μ 1 2= μ 1 =… 3 μ 11 … = фазы компоненты k μ 1
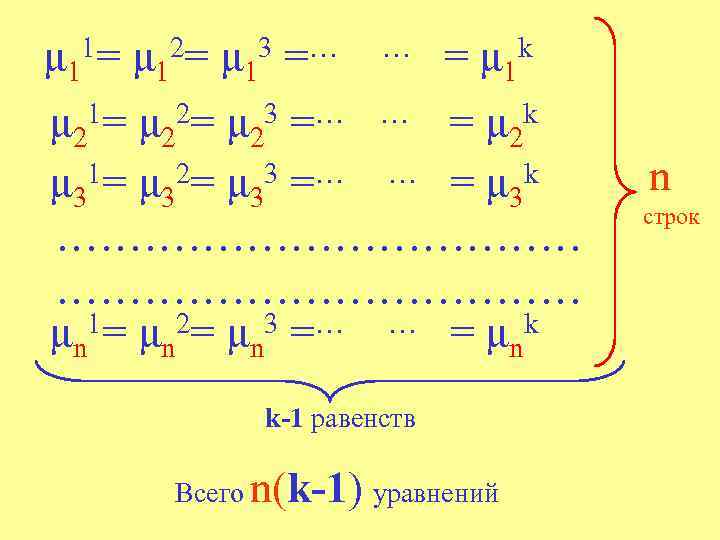
μ 11= μ 12= μ 13 =… … = μ 1 k 1= μ 2= μ 3 =… … = μ k μ 2 2 1= μ 2= μ 3 =… … =μ k μ 3 3 ……………………………… μn 1= μn 2= μn 3 =… … = μnk k-1 равенств Всего n(k-1) уравнений n строк

Система уравнений имеет определенное решение, если число уравнений равно числу переменных. Переменные: Состав равновесных фаз Температура Давление Другие внешние потенциалы, влияющие на состояние системы (? ? ? )
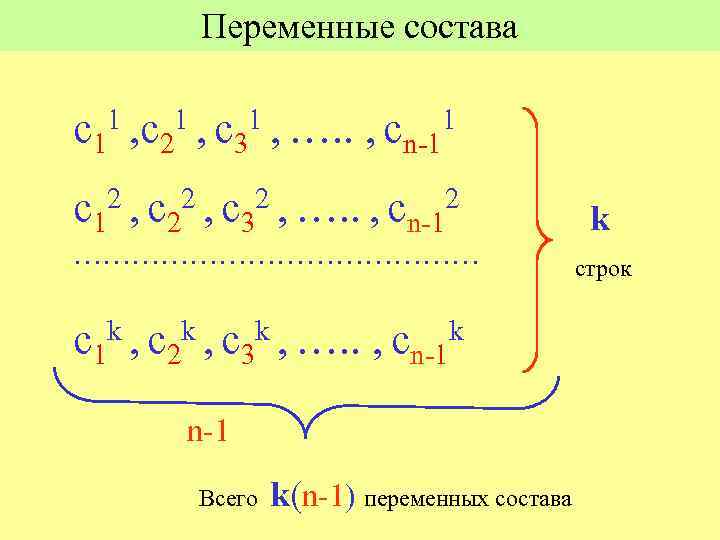
Переменные состава с11 , с21 , с31 , …. . , cn-11 с12 , с22 , с32 , …. . , cn-12 ………………… k , с k , …. . с1 2 3 k , сn-1 Всего k(n-1) переменных состава k строк
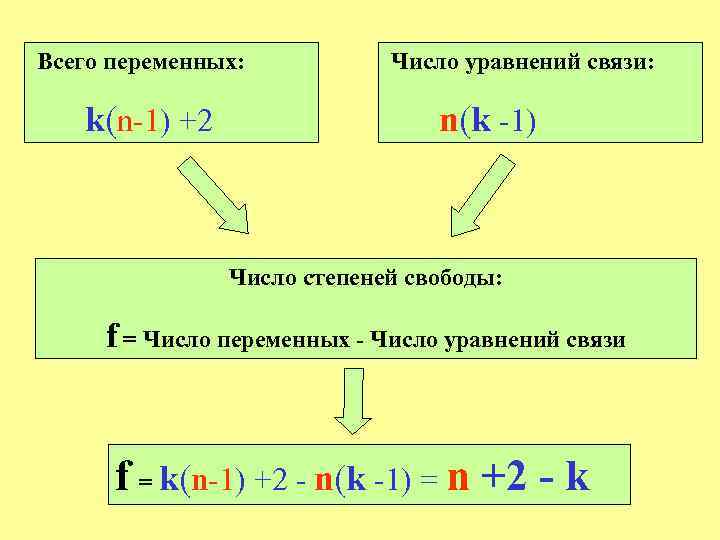
Всего переменных: Число уравнений связи: k(n-1) +2 n(k -1) Число степеней свободы: f = Число переменных - Число уравнений связи f = k(n-1) +2 - n(k -1) = n +2 - k
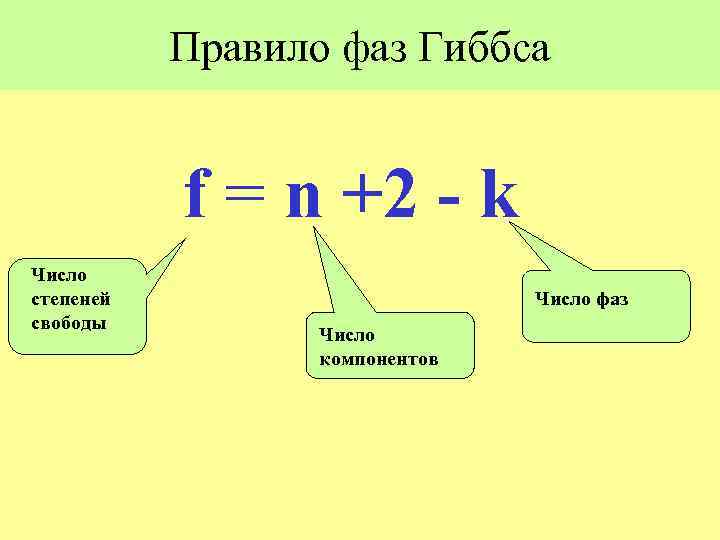
Правило фаз Гиббса f = n +2 - k Число степеней свободы Число фаз Число компонентов

f = n +2 - k !!!

Принцип соответствия Всякому комплексу фаз на диаграмме состояния соответствует свой геометрический образ, причем мерность этого образа равна вариантности системы в данном равновесном комплексе.
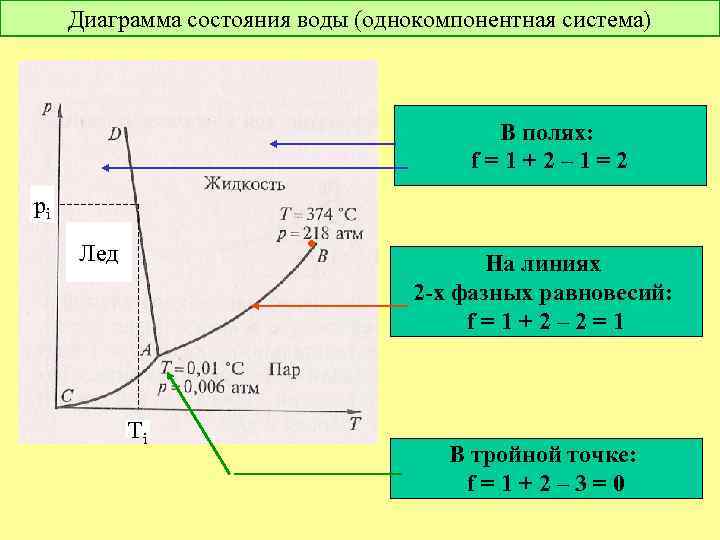
Диаграмма состояния воды (однокомпонентная система) В полях: f = 1 + 2 – 1 = 2 pi • Лед Ti На линиях 2 -х фазных равновесий: f = 1 + 2 – 2 = 1 В тройной точке: f = 1 + 2 – 3 = 0
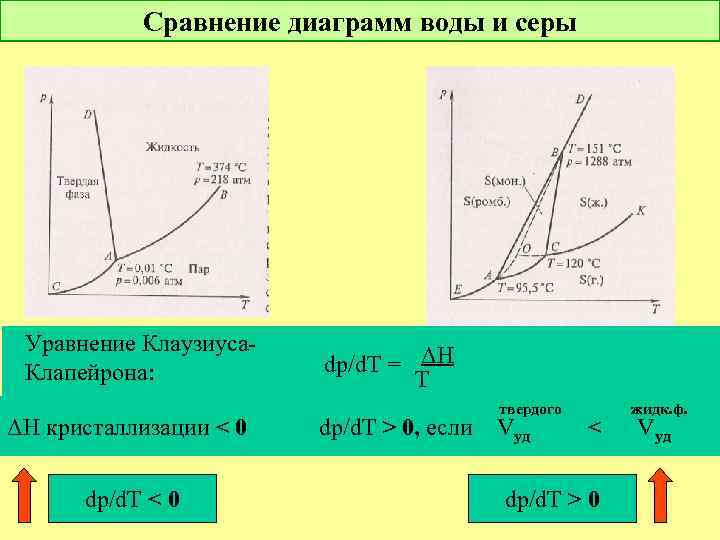
Сравнение диаграмм воды и серы Уравнение Клаузиуса. Клапейрона: dp/d. T = ΔH T Δv ΔH кристаллизации < 0 dp/d. T > 0, если dp/d. T < 0 твердого жидк. ф. Vуд < Vуд dp/d. T > 0
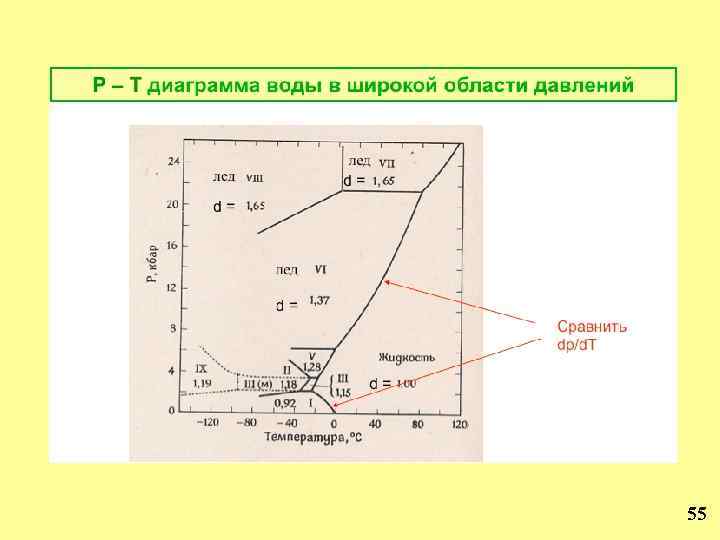
55
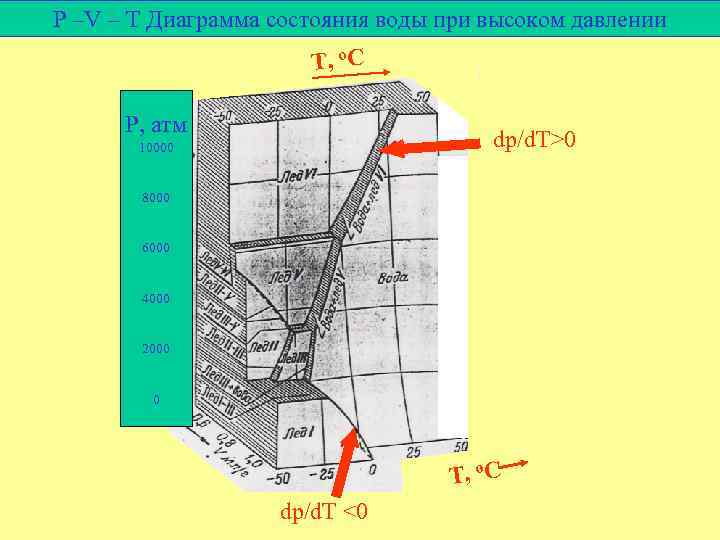
P –V – T Диаграмма состояния воды при высоком давлении T, o C P, атм dp/d. T>0 10000 8000 6000 4000 2000 0 T, o C dp/d. T <0
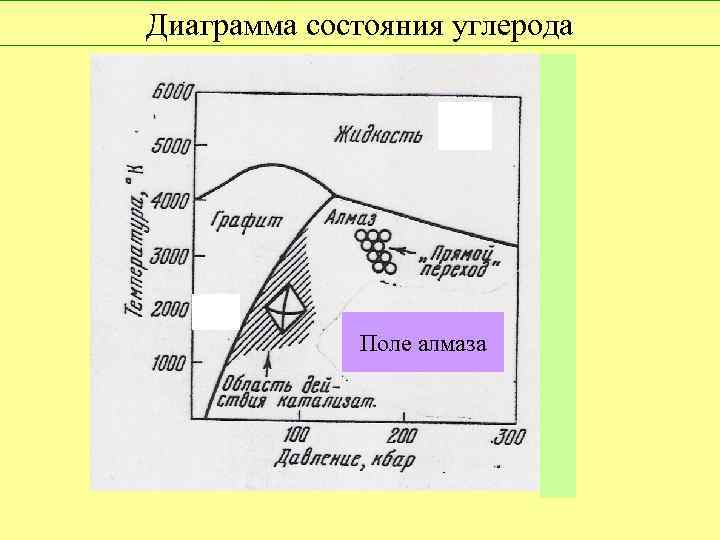
Диаграмма состояния углерода Поле алмаза
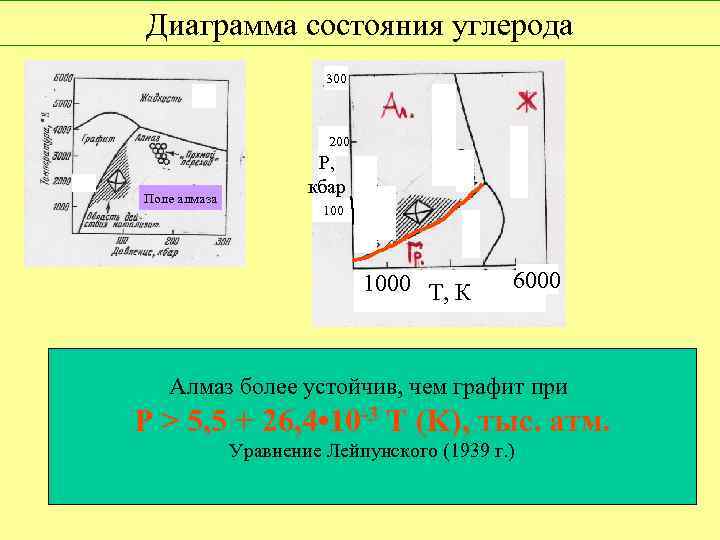
Диаграмма состояния углерода 300 200 Поле алмаза Р, кбар 1000 Т, К 6000 Алмаз более устойчив, чем графит при P > 5, 5 + 26, 4 • 10 -3 T (K), тыс. атм. Уравнение Лейпунского (1939 г. )
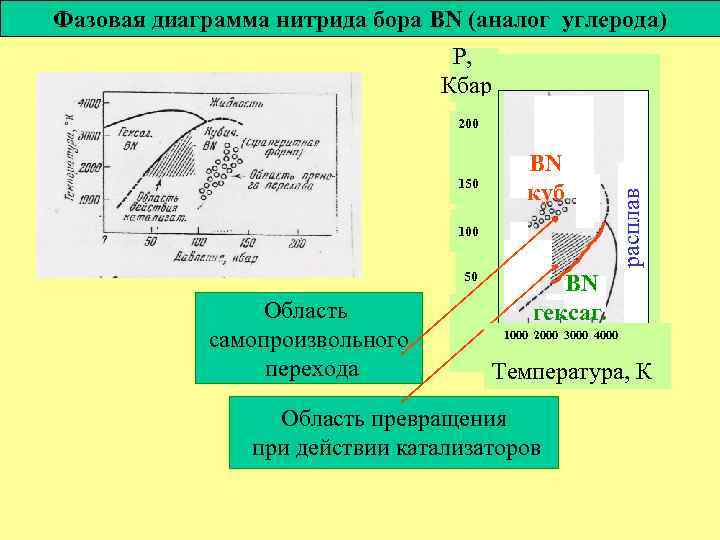
Фазовая диаграмма нитрида бора BN (аналог углерода) Р, Кбар 150 BN куб 100 50 Область самопроизвольного перехода расплав 200 BN гексаг. 1000 2000 3000 4000 Температура, К Область превращения при действии катализаторов

Кубический нитрид бора – высокотвердый материал для режущих инструментов BN, в отличие от алмаза, инертен по отношению к Fe и поэтому может быть использован для высокоскоростной обработки черных металлов (сталей и чугунов).

Двухкомпонентные (бинарные) системы

Классификация равновесий в бинарных системах по признаку вариантности (Р=const) Инконгруэнтные Конгруэнтные 2 -фазные 3 -фазные 1. Изоморфные смеси с экстремумом на кривой равновесия Изоморфные смеси без экстремума на кривой равновесия f =1 +1 – 2 =0 f =2 +1 – 2 =1 в равновесии А) жидкость – пар Б) жидкость – тв. раствор В) тв. раствор 1 -тв. раствор 2 2. Конгруэнтное плавление (испарение, сублимация) химических соединений в равновесии А) жидкость – пар Б) жидкость – тв. раствор В) тв. раствор 1 -тв. раствор 2 f =2 +1 – 3 =0 В равновесии комбинации фаз в различных агрегатных состояниях: Ж – Тв – Г 1, 2, 3 А) при охлаждении 1 2 + 3 Б) при охлаждении 2 + 3 1
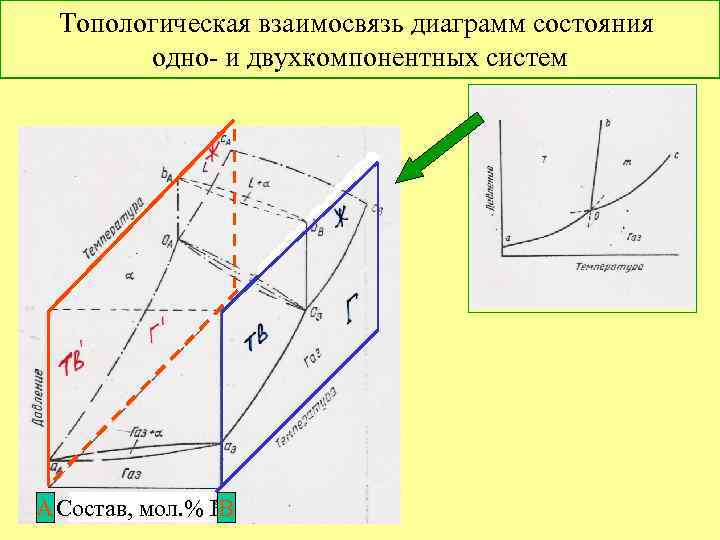
Топологическая взаимосвязь диаграмм состояния одно- и двухкомпонентных систем А Состав, мол. % В В
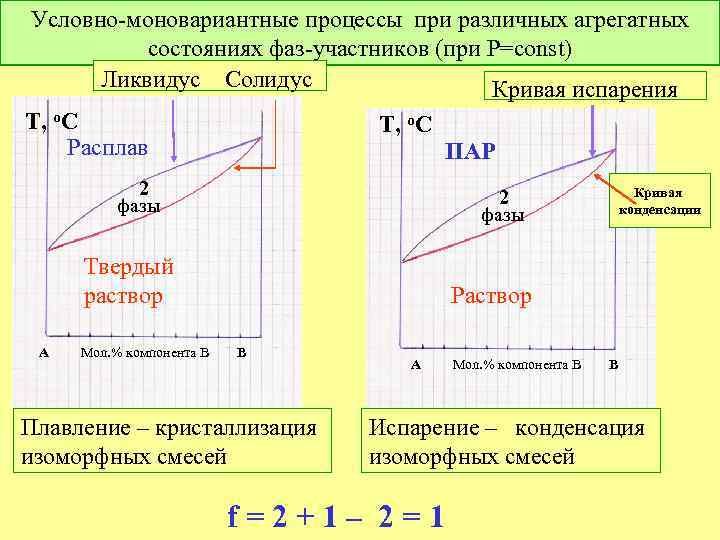
Условно-моновариантные процессы при различных агрегатных состояниях фаз-участников (при Р=const) Ликвидус Солидус Кривая испарения Т, о. С Расплав Т, о. С 2 фазы Твердый раствор А Мол. % компонента В ПАР Кривая конденсации Раствор В Плавление – кристаллизация изоморфных смесей А Мол. % компонента В В Испарение – конденсация изоморфных смесей f = 2 + 1 – 2 = 1
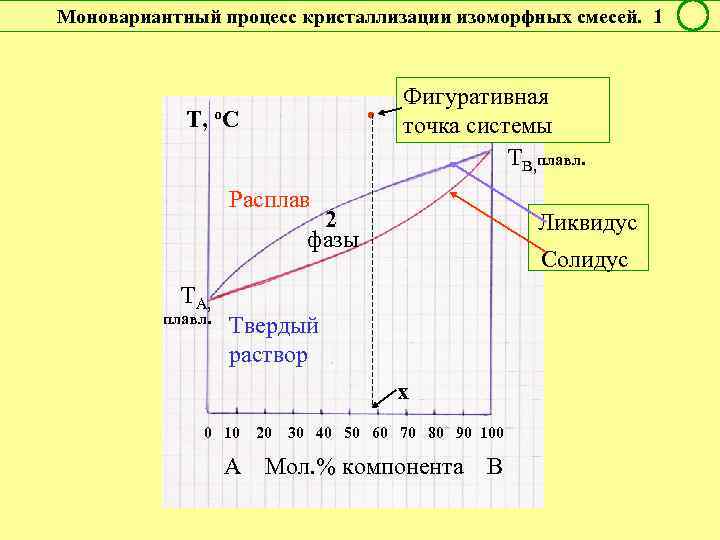
Моновариантный процесс кристаллизации изоморфных смесей. 1 • Т, о. С Фигуративная точка системы ТВ, плавл. Расплав 2 фазы ТА, плавл. Ликвидус Солидус Твердый раствор х 0 10 20 30 40 50 60 70 80 90 100 А Мол. % компонента В
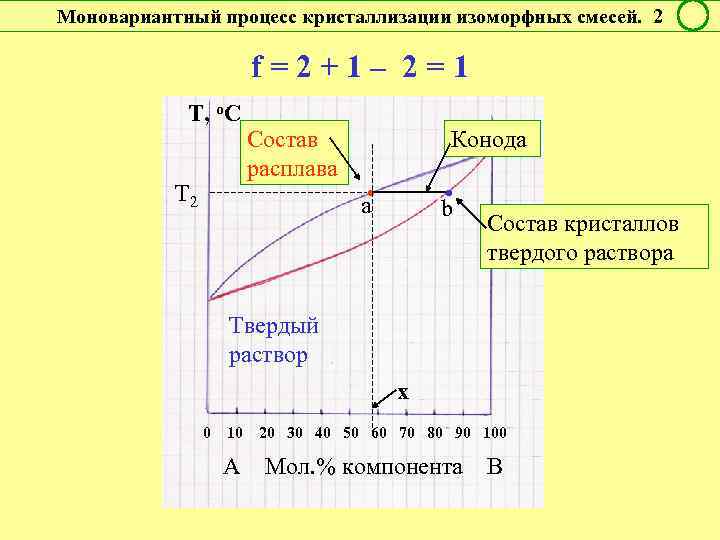
Моновариантный процесс кристаллизации изоморфных смесей. 2 f = 2 + 1 – 2 = 1 Т, о. С Т 2 Состав расплава Конода а • • b Состав кристаллов твердого раствора Твердый раствор х 0 10 20 30 40 50 60 70 80 90 100 А Мол. % компонента В
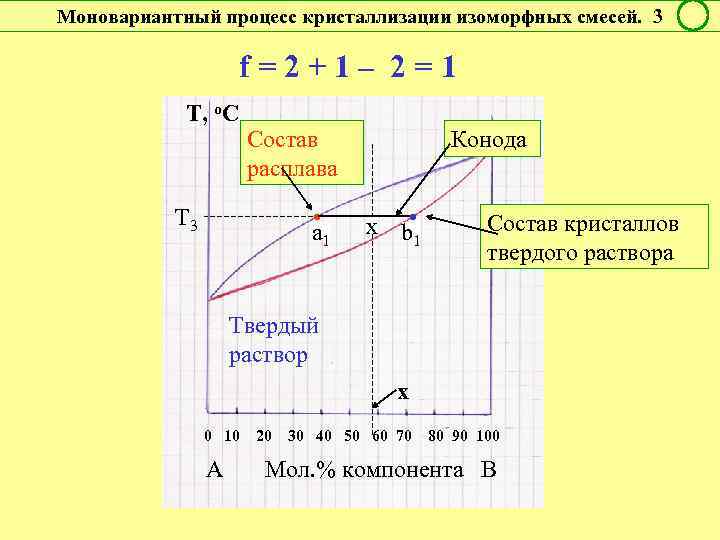
Моновариантный процесс кристаллизации изоморфных смесей. 3 f = 2 + 1 – 2 = 1 Т, о. С Т 3 Конода Состав расплава • a 1 x b • 1 Состав кристаллов твердого раствора Твердый раствор х 0 10 20 30 40 50 60 70 80 90 100 А Мол. % компонента В
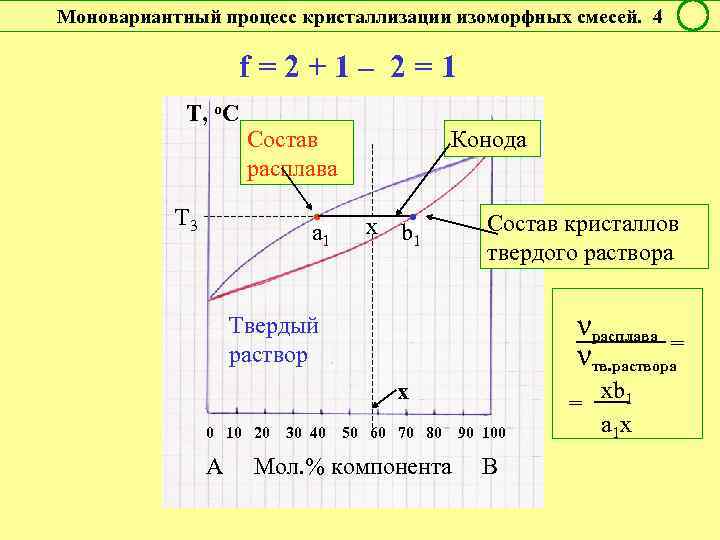
Моновариантный процесс кристаллизации изоморфных смесей. 4 f = 2 + 1 – 2 = 1 Т, о. С Т 3 Конода Состав расплава • a 1 x b • 1 Состав кристаллов твердого раствора νрасплава = νтв. раствора Твердый раствор х = 0 10 20 30 40 50 60 70 80 90 100 А Мол. % компонента В xb 1 a 1 x

Правило рычага Соотношение масс (чисел молей ) равновесных фаз – участников двухфазного инконгруэнтного процесса - обратно отношению отрезков коноды от фигуративных точек этих фаз до фигуративной точки системы. ! Если состав в % мас. : mα / m. L = x. L / xα Если состав в % мол. : να / νL = x. L / xα α m α , να х L m. L, νL
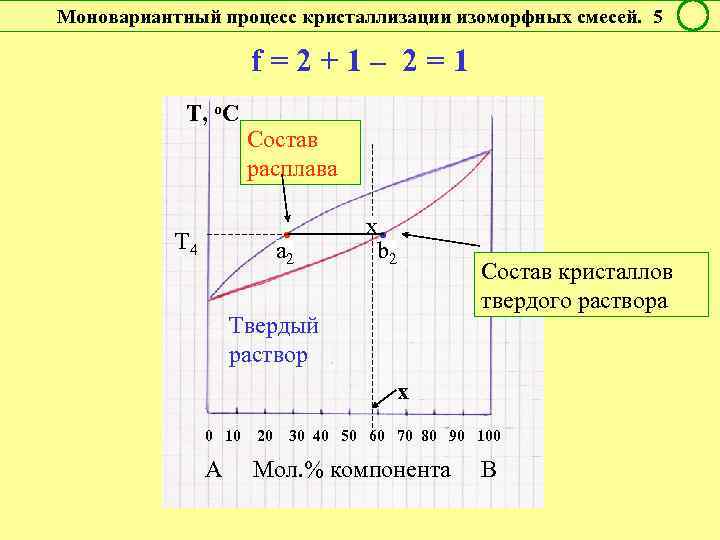
Моновариантный процесс кристаллизации изоморфных смесей. 5 f = 2 + 1 – 2 = 1 Т, о. С Состав расплава • a 2 Т 4 x • b 2 Состав кристаллов твердого раствора Твердый раствор х 0 10 20 30 40 50 60 70 80 90 100 А Мол. % компонента В
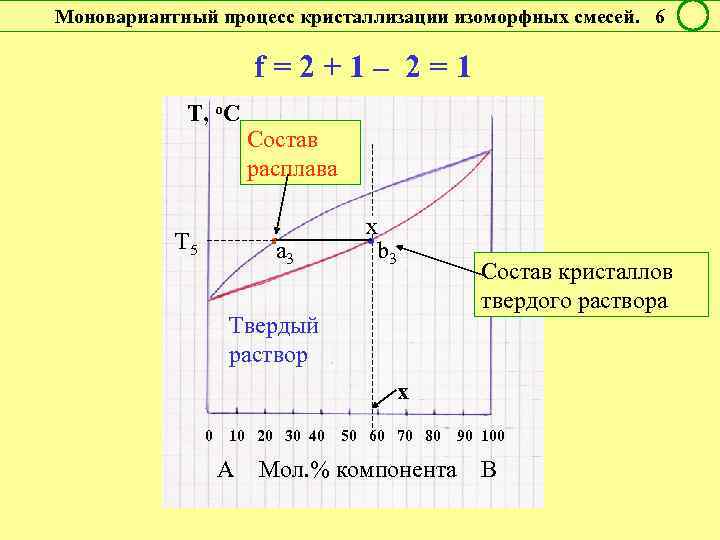
Моновариантный процесс кристаллизации изоморфных смесей. 6 f = 2 + 1 – 2 = 1 Т, о. С Т 5 Состав расплава • a 3 x • b 3 Состав кристаллов твердого раствора Твердый раствор х 0 10 20 30 40 50 60 70 80 90 100 А Мол. % компонента В

Инконгруэнтные превращения в изоморфных смесях f = 2 + 1 – 2 = 1 Условно моновариантное превращение Смысл моновариантности (f = 1): 1. Состав обеих равновесных фаз однозначно определяется температурой. Для определения состава фаз надо провести коноду при выбранной температуре. 2. Данный состав фазы может быть реализован только при вполне определенной температуре. Этому составу равновесна вторая фаза также вполне определенного состава.

73
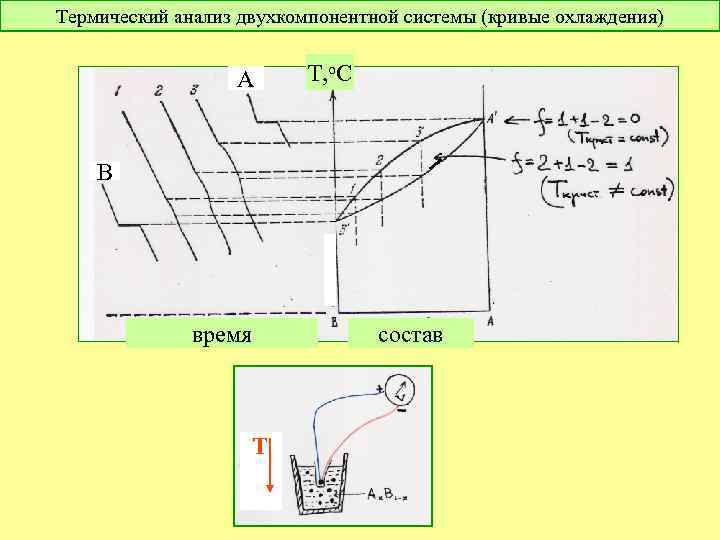
Термический анализ двухкомпонентной системы (кривые охлаждения) А Т, о. С В время состав Т
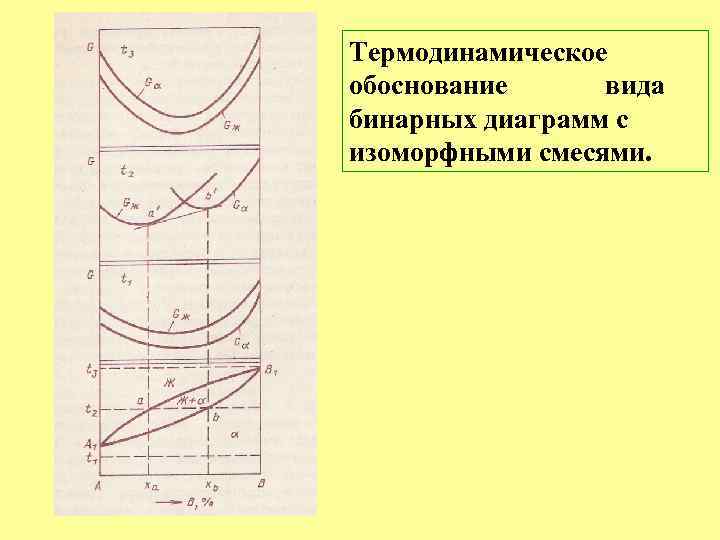
Термодинамическое обоснование вида бинарных диаграмм с изоморфными смесями.
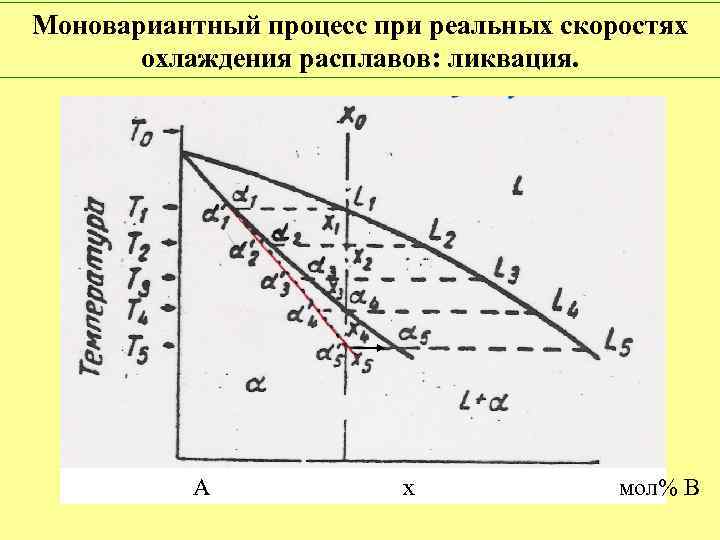
Моновариантный процесс при реальных скоростях охлаждения расплавов: ликвация. А х мол% В
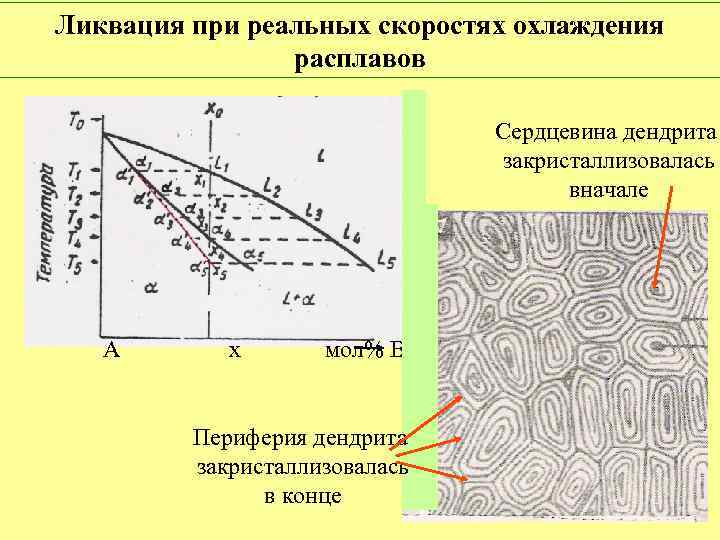
Ликвация при реальных скоростях охлаждения расплавов Сердцевина дендрита закристаллизовалась вначале А х мол% В Периферия дендрита закристаллизовалась в конце
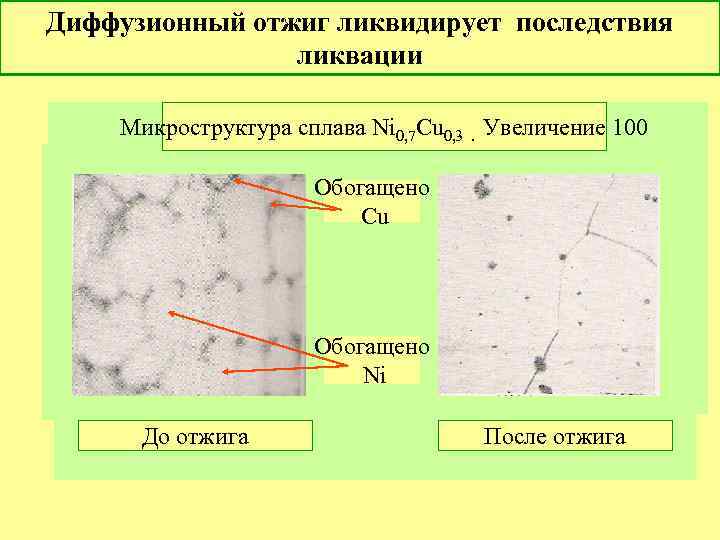
Диффузионный отжиг ликвидирует последствия ликвации Микроструктура сплава Ni 0, 7 Cu 0, 3. Увеличение 100 Обогащено Cu Обогащено Ni До отжига После отжига
При ликвации остатки расплава сохраняются до T < T равновесного солидуса. При нагреве сплавов, подвергшихся ликвации, расплав появляется при T < T равновесного солидуса. Горячеломкость сплавов, подвергшихся ликвации
Lectures 1_2-11.ppt