Избранные главы неорганического материаловедения Лекция 6 Трехкомпонентные (тройные)


Избранные главы неорганического материаловедения Лекция 6 Трехкомпонентные (тройные) системы Способы изображения состава. Объемные диаграммы плавкости. Изотермические сечения.
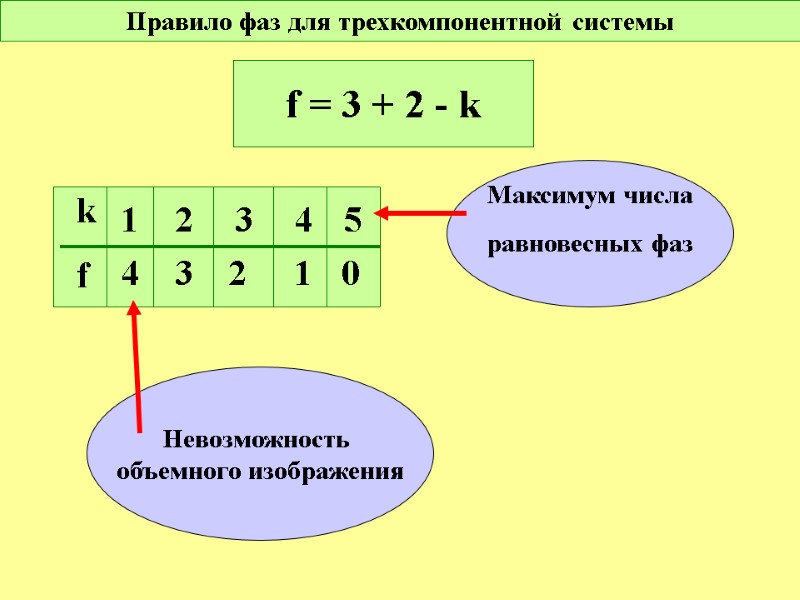
Правило фаз для трехкомпонентной системы f = 3 + 2 - k k f 1 2 3 4 5 4 3 2 1 0 Максимум числа равновесных фаз Невозможность объемного изображения
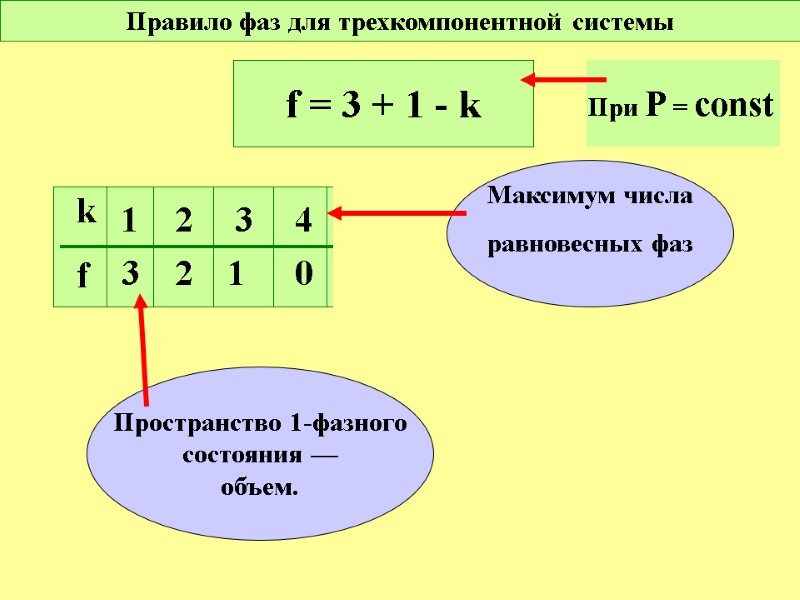
Правило фаз для трехкомпонентной системы f = 3 + 1 - k k f 1 2 3 4 5 3 2 1 0 0 Максимум числа равновесных фаз Пространство 1-фазного состояния — объем. При Р = const
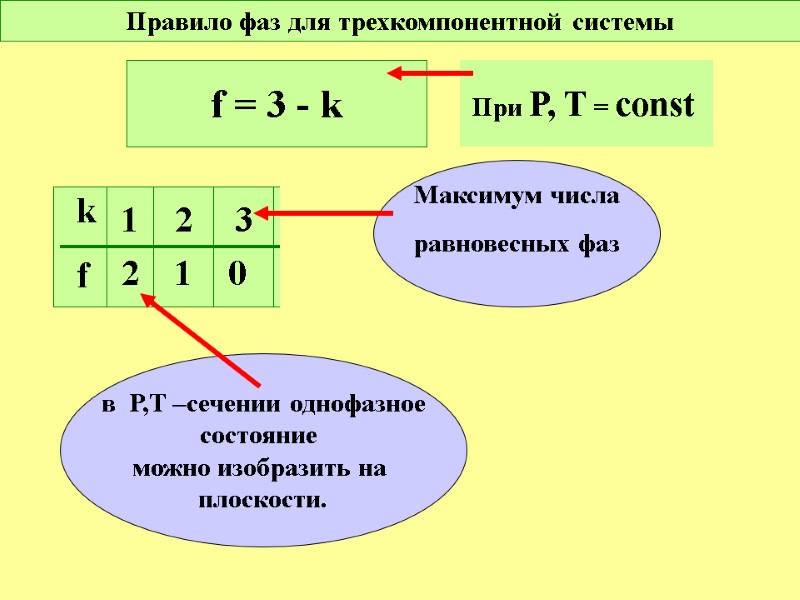
Правило фаз для трехкомпонентной системы f = 3 - k k f 1 2 3 4 5 2 1 0 0 0 Максимум числа равновесных фаз в Р,Т –сечении однофазное состояние можно изобразить на плоскости. При Р, T = const
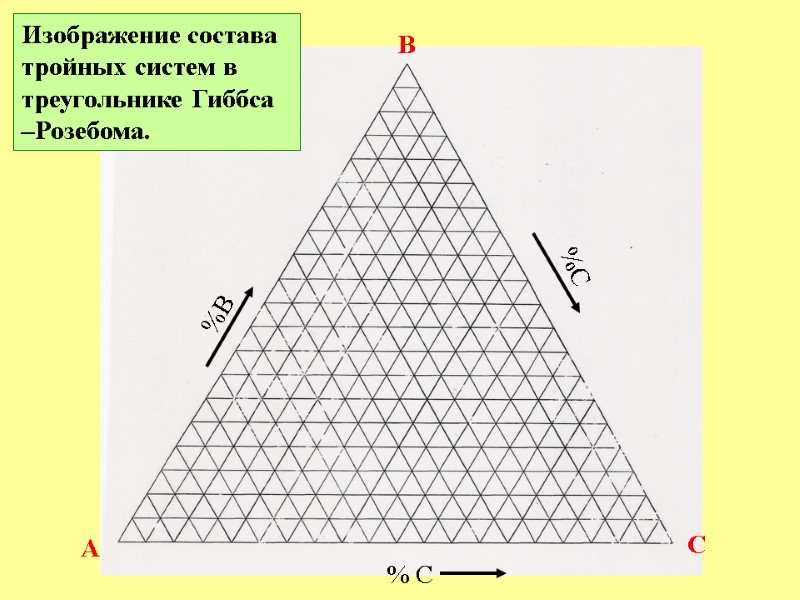
A B C % C %B %C Изображение состава тройных систем в треугольнике Гиббса –Розебома.
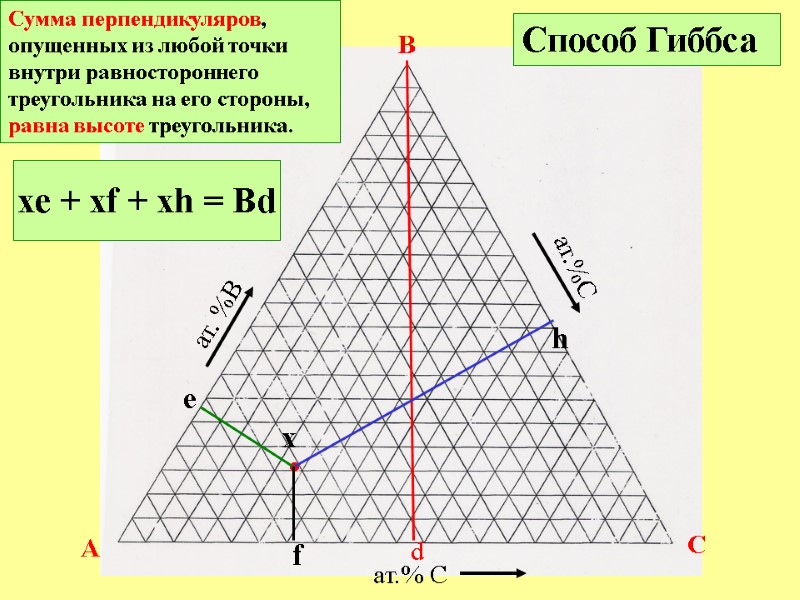
A B C ат.% C ат. %B ат.%C Сумма перпендикуляров, опущенных из любой точки внутри равностороннего треугольника на его стороны, равна высоте треугольника. Способ Гиббса d • x e f h xe + xf + xh = Bd
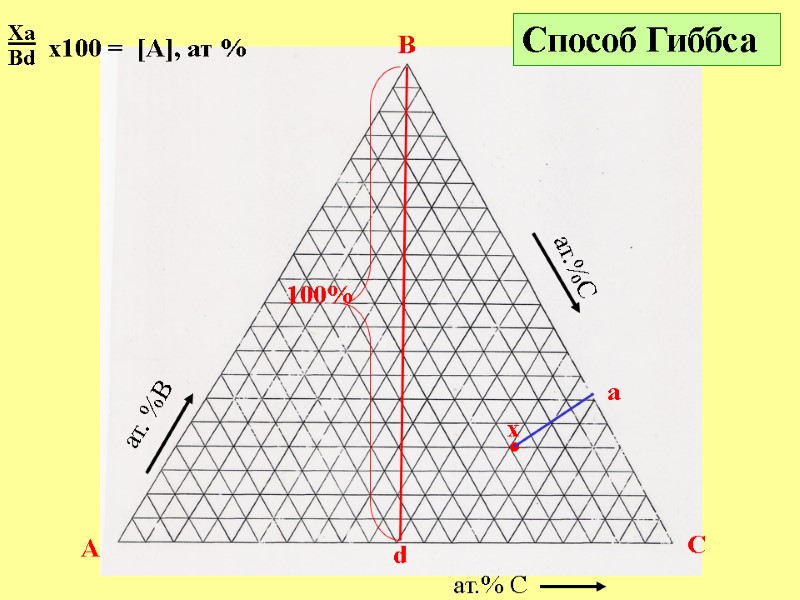
A B C ат.% C ат. %B ат.%C Xa Bd • Способ Гиббса 100% d x a x100 = [A], ат %
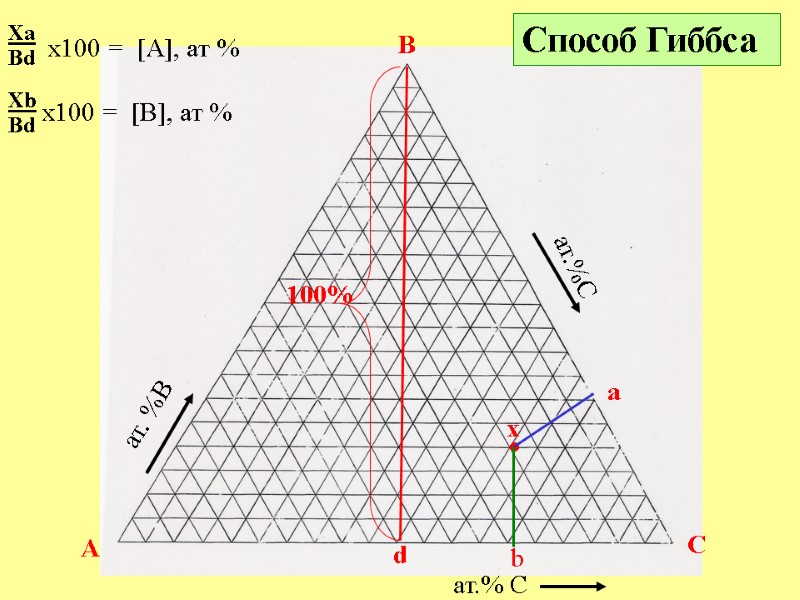
A B C ат.% C ат. %B ат.%C Xa Bd • Способ Гиббса 100% d x a x100 = [A], ат % Xb Bd x100 = [В], ат % b
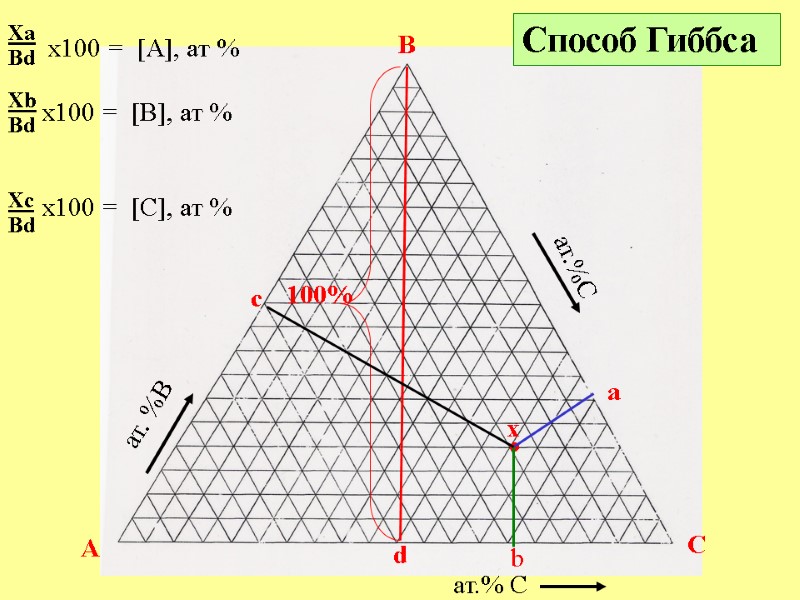
A B C ат.% C ат. %B ат.%C Xa Bd • Способ Гиббса 100% d x a x100 = [A], ат % Xb Bd x100 = [В], ат % Xc Bd x100 = [С], ат % b c
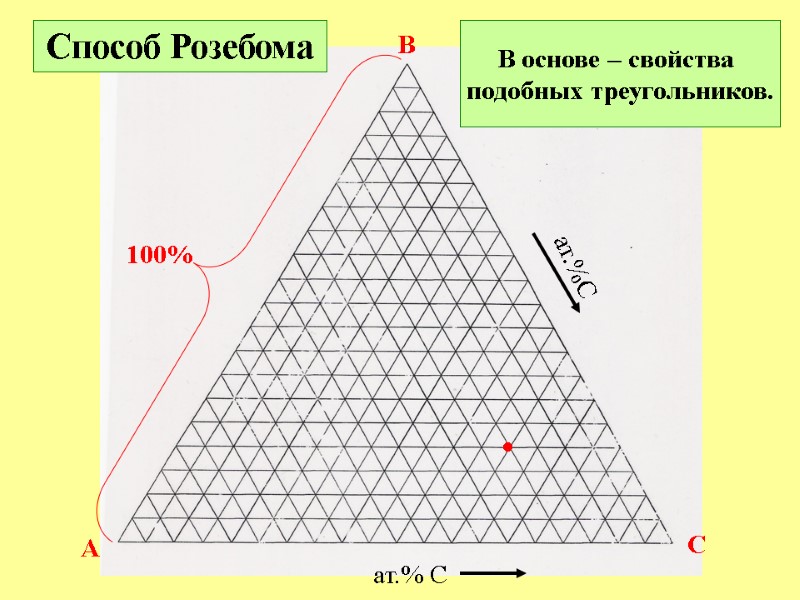
A B C ат.% C ат.%C • Способ Розебома 100% В основе – свойства подобных треугольников.
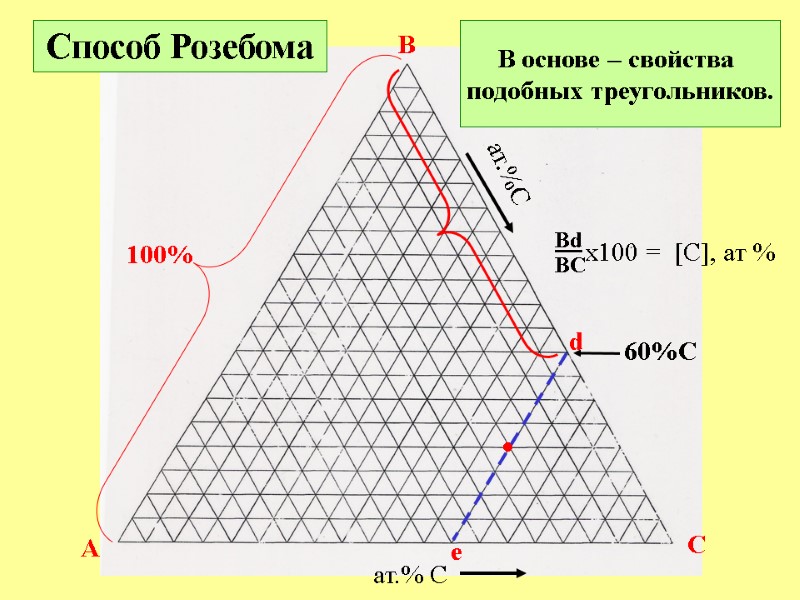
A B C ат.% C ат.%C • Способ Розебома 100% В основе – свойства подобных треугольников. d e Bd BC x100 = [С], ат % 60%C
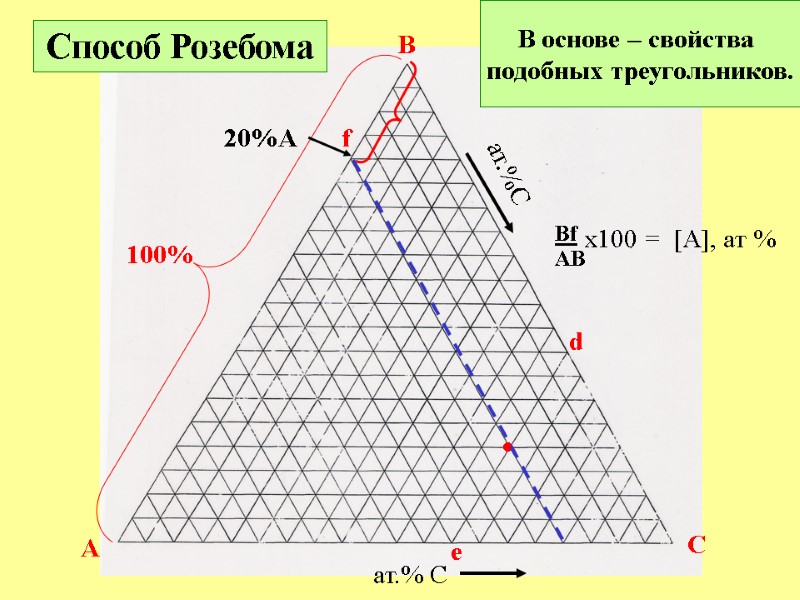
A B C ат.% C ат.%C • Способ Розебома 100% В основе – свойства подобных треугольников. d e Bf AB x100 = [A], ат % 20%A f
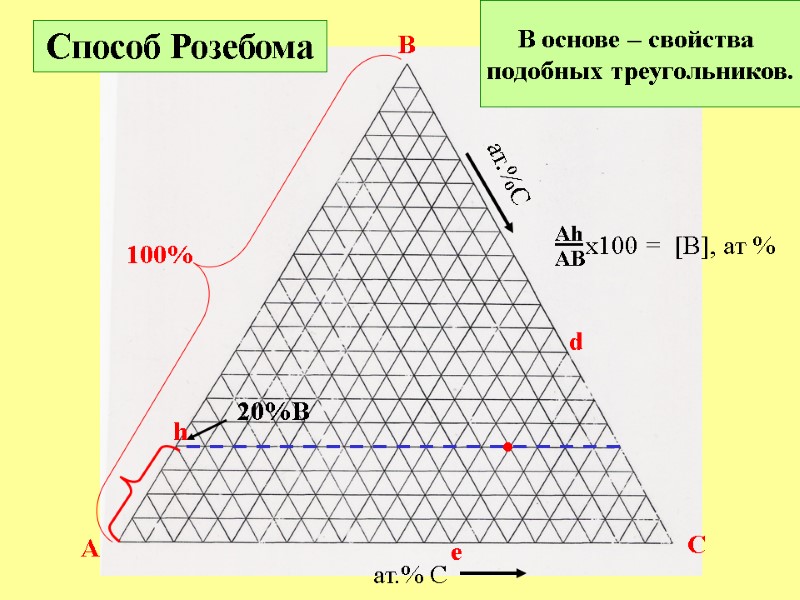
A B C ат.% C ат.%C • Способ Розебома 100% В основе – свойства подобных треугольников. d e Ah AB x100 = [B], ат % 20%B h
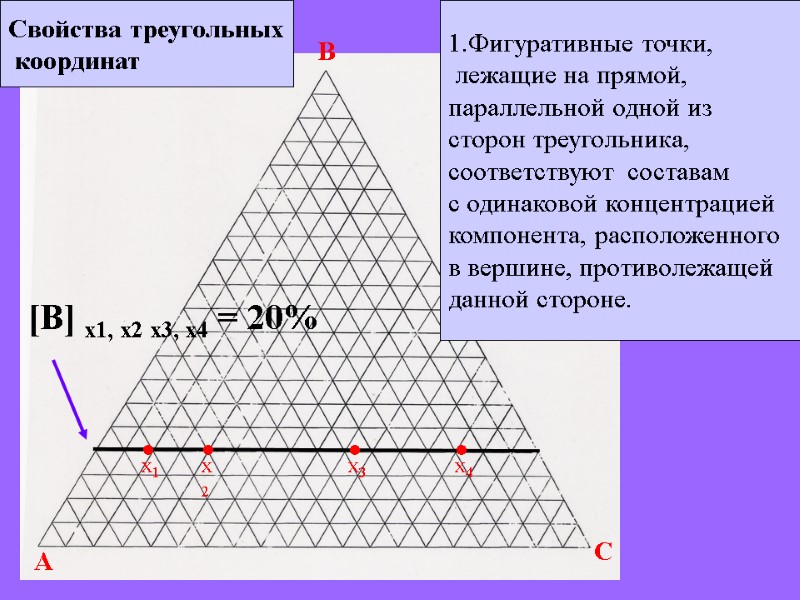
A B C Свойства треугольных координат 1.Фигуративные точки, лежащие на прямой, параллельной одной из сторон треугольника, соответствуют составам с одинаковой концентрацией компонента, расположенного в вершине, противолежащей данной стороне. х1 х2 х3 х4 • • • • [B] x1, x2 x3, x4 = 20%
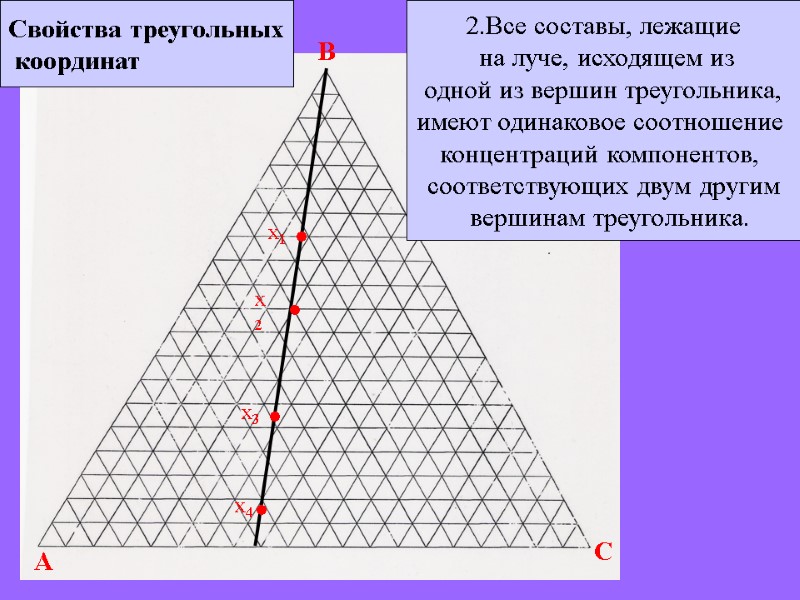
A B C Свойства треугольных координат 2.Все составы, лежащие на луче, исходящем из одной из вершин треугольника, имеют одинаковое соотношение концентраций компонентов, соответствующих двум другим вершинам треугольника. х1 х2 х3 х4 • • • •
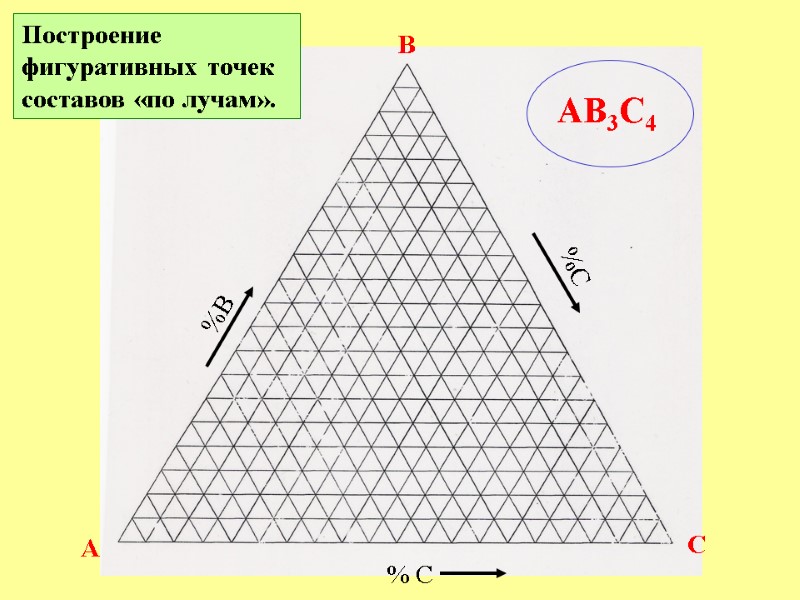
A B C % C %B %C Построение фигуративных точек составов «по лучам». АВ3С4
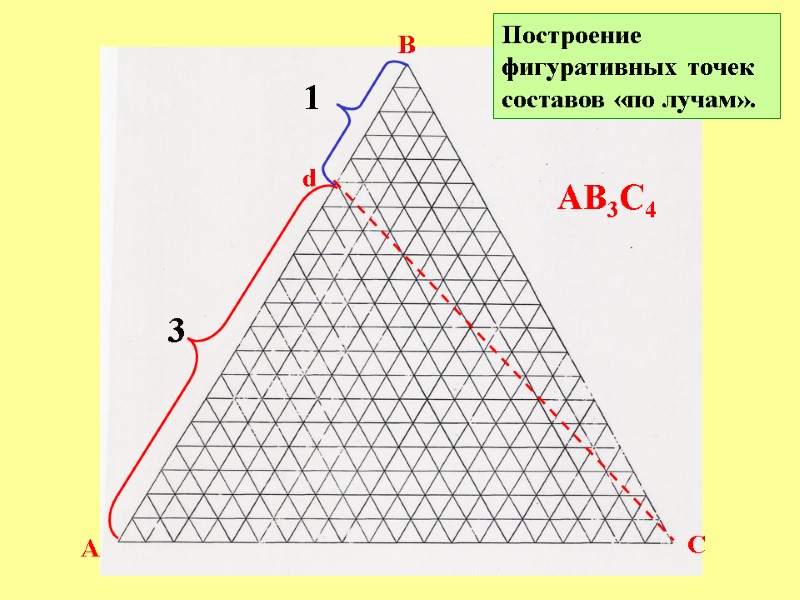
A B C Построение фигуративных точек составов «по лучам». АВ3С4 d 3 1
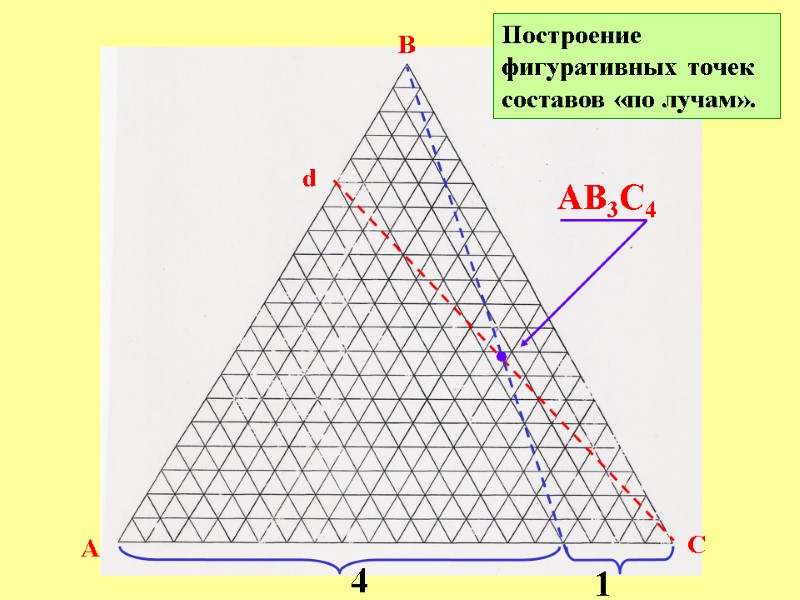
A B C Построение фигуративных точек составов «по лучам». АВ3С4 d 4 1 •
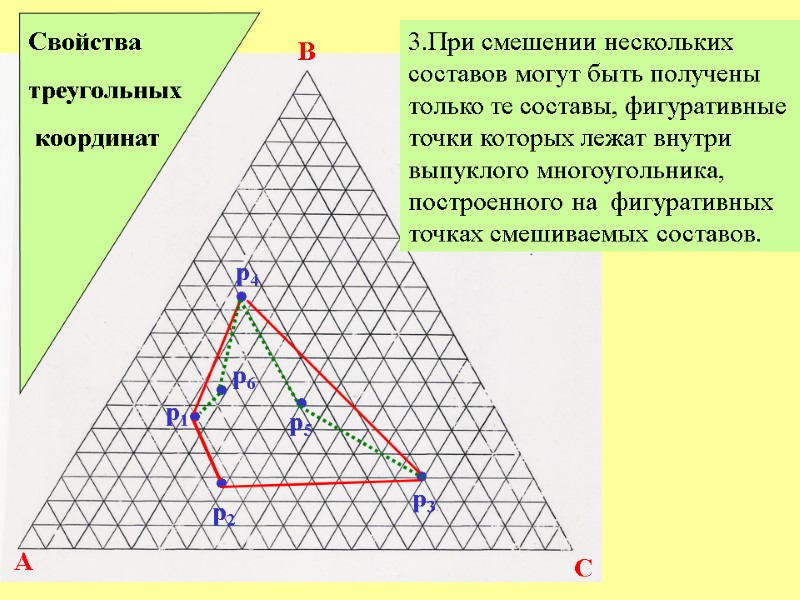
A B C р1 Свойства треугольных координат 3.При смешении нескольких составов могут быть получены только те составы, фигуративные точки которых лежат внутри выпуклого многоугольника, построенного на фигуративных точках смешиваемых составов. р2 р3 • • • • • • р4 р5 р6
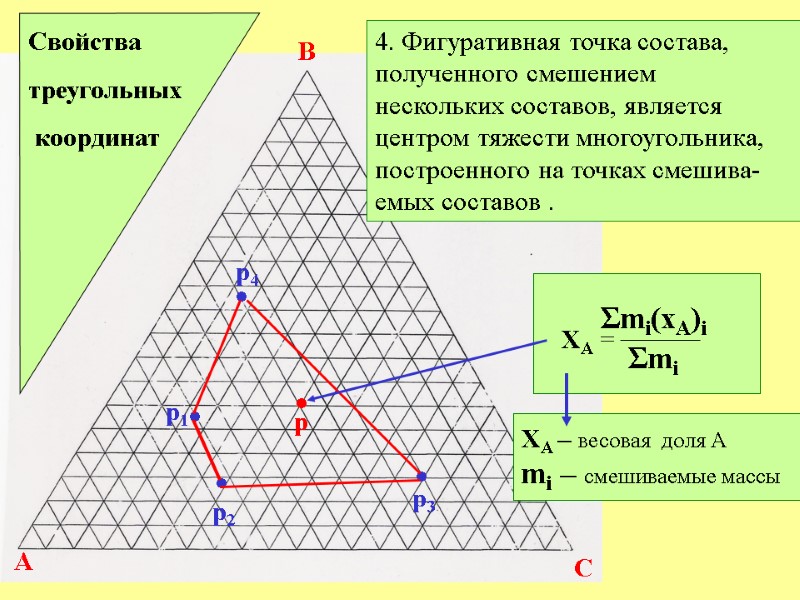
A B C р1 Свойства треугольных координат 4. Фигуративная точка состава, полученного смешением нескольких составов, является центром тяжести многоугольника, построенного на точках смешива- емых составов . р2 р3 • • • • • р4 р ХА = Σmi(xA)i Σmi ХА – весовая доля А mi – смешиваемые массы
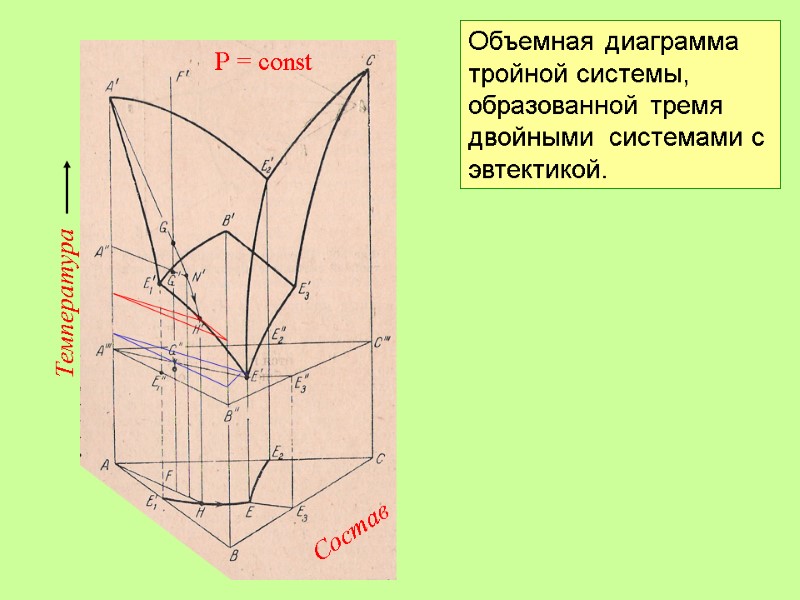
Температура Состав Р = const Объемная диаграмма тройной системы, образованной тремя двойными системами с эвтектикой.
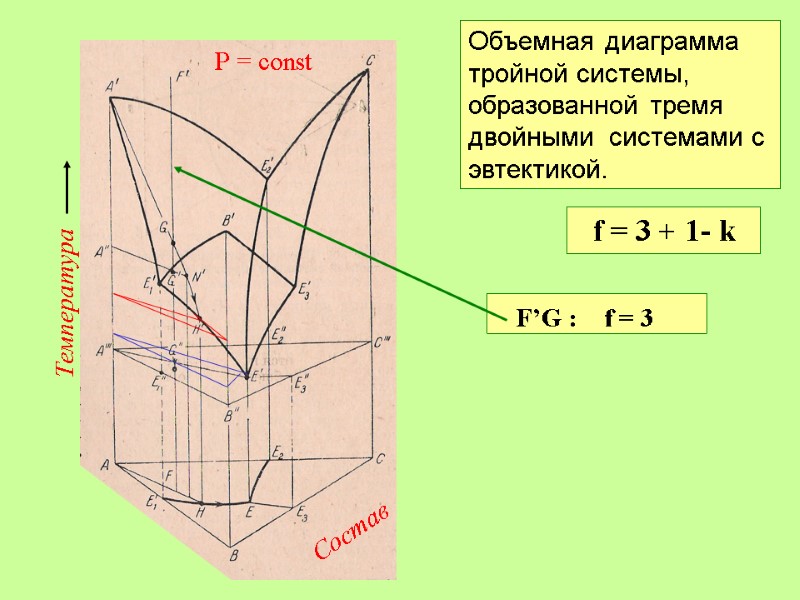
Температура Состав Р = const Объемная диаграмма тройной системы, образованной тремя двойными системами с эвтектикой. f = 3 + 1- k F’G : f = 3 GH’ : f = 2 H’E’: f = 1 E’: f = 0
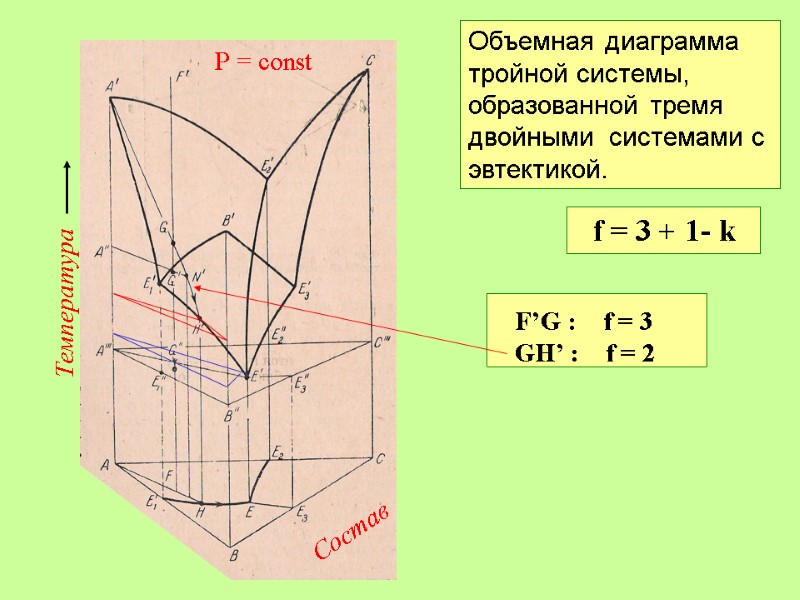
Температура Состав Р = const Объемная диаграмма тройной системы, образованной тремя двойными системами с эвтектикой. f = 3 + 1- k F’G : f = 3 GH’ : f = 2 H’E’: f = 1 E’: f = 0
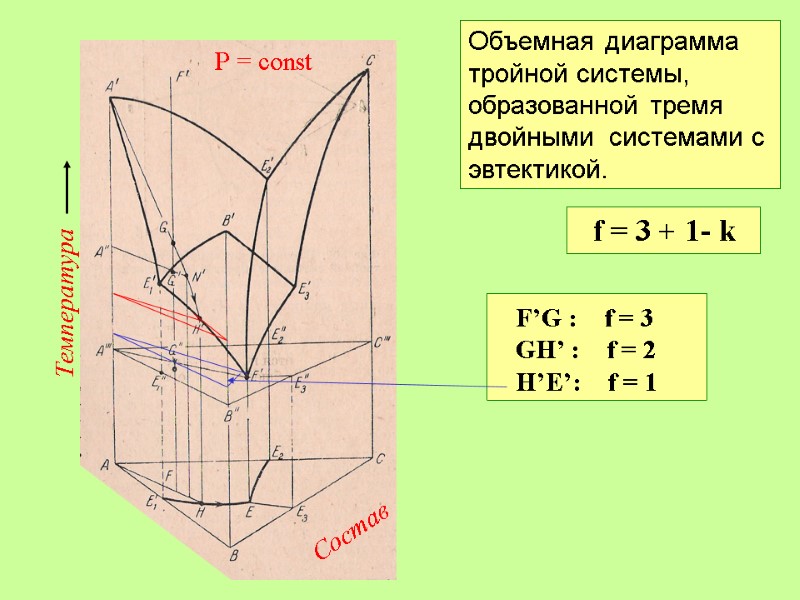
Температура Состав Р = const Объемная диаграмма тройной системы, образованной тремя двойными системами с эвтектикой. f = 3 + 1- k F’G : f = 3 GH’ : f = 2 H’E’: f = 1 E’: f = 0
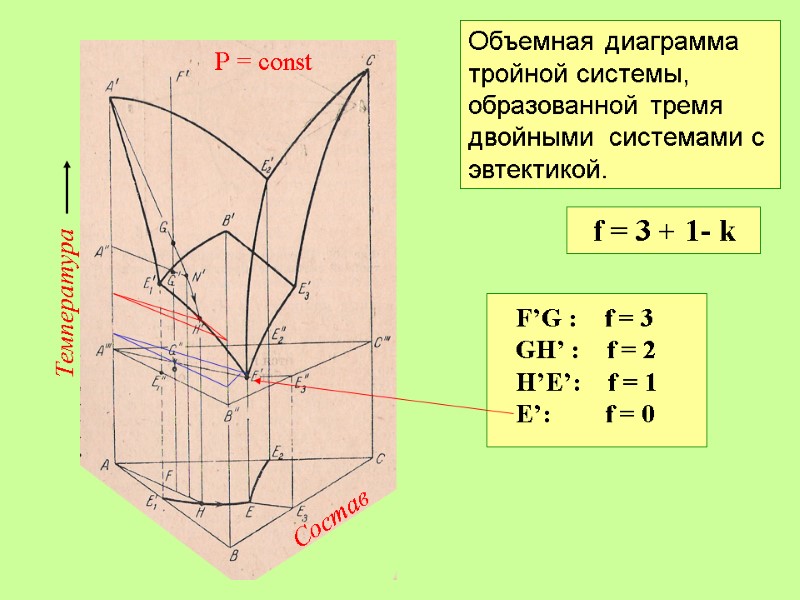
Температура Состав Р = const Объемная диаграмма тройной системы, образованной тремя двойными системами с эвтектикой. f = 3 + 1- k F’G : f = 3 GH’ : f = 2 H’E’: f = 1 E’: f = 0
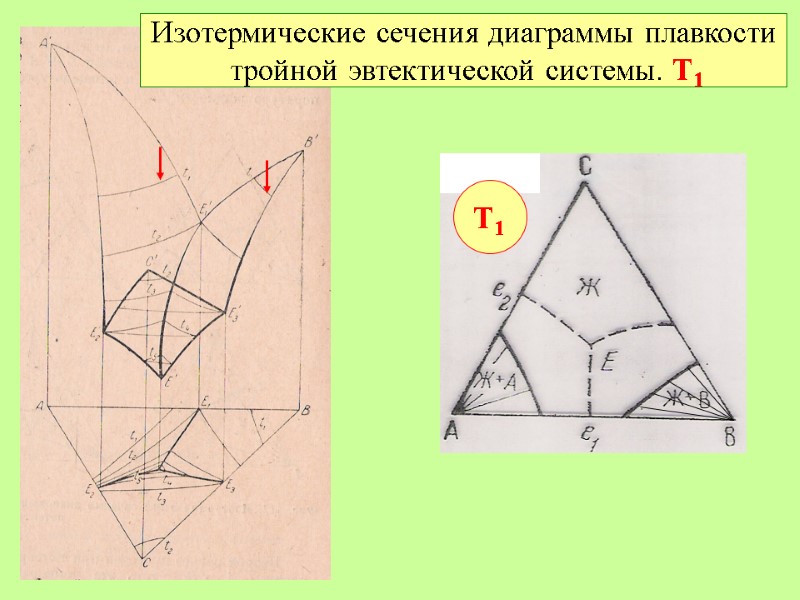
Изотермические сечения диаграммы плавкости тройной эвтектической системы. Т1 Т1
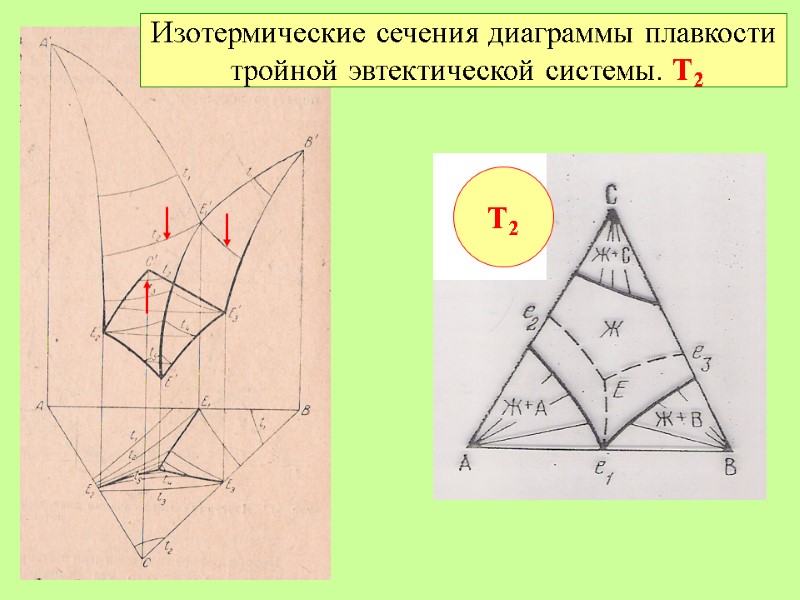
Изотермические сечения диаграммы плавкости тройной эвтектической системы. Т2 Т2
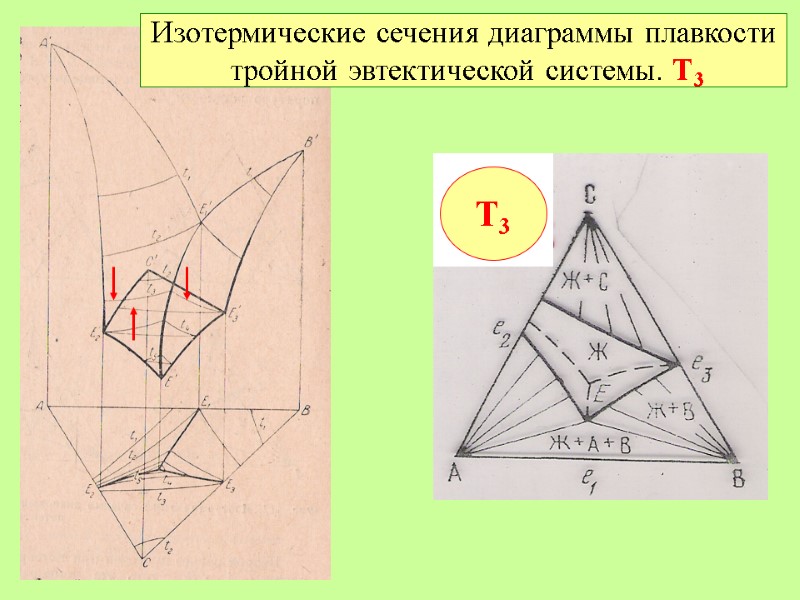
Изотермические сечения диаграммы плавкости тройной эвтектической системы. Т3 Т3
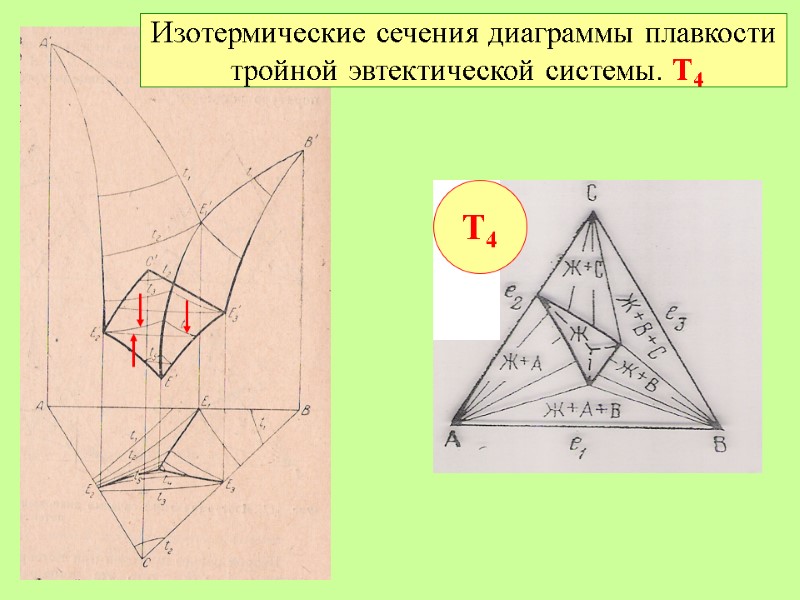
Изотермические сечения диаграммы плавкости тройной эвтектической системы. Т4 Т4
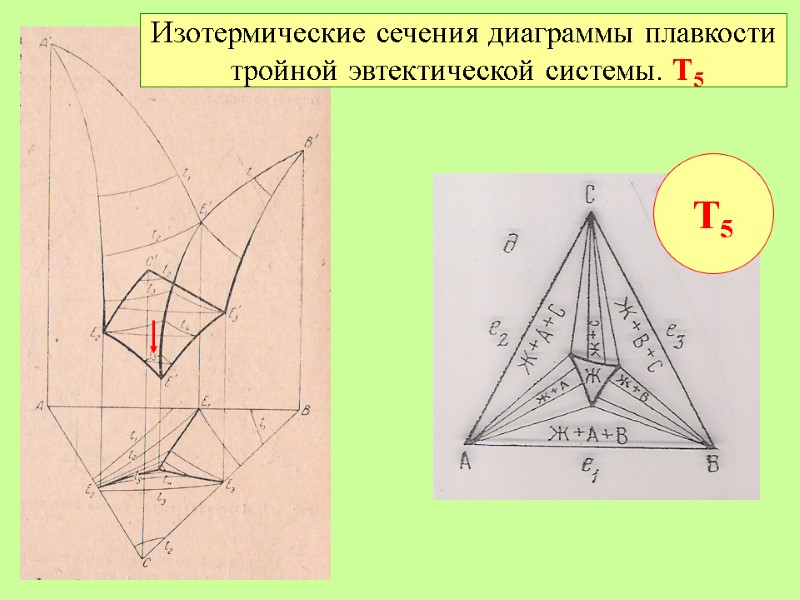
Изотермические сечения диаграммы плавкости тройной эвтектической системы. Т5 Т5
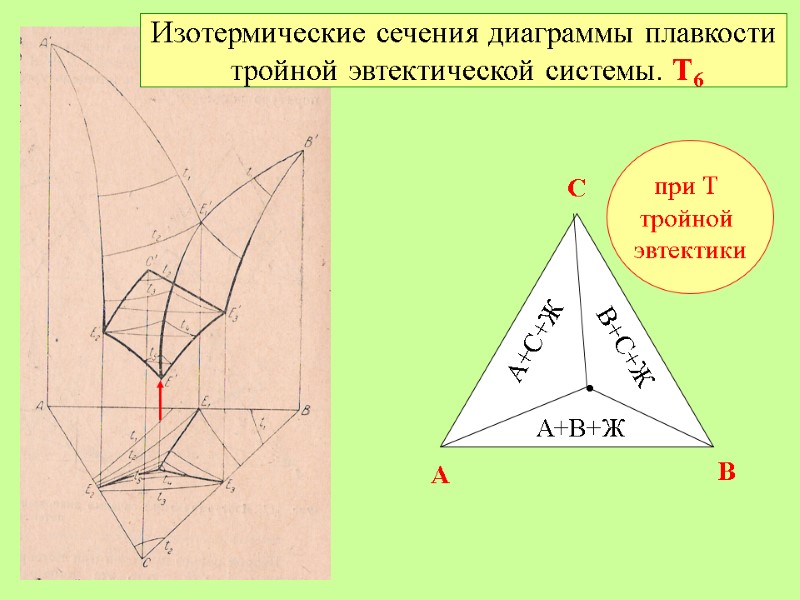
Изотермические сечения диаграммы плавкости тройной эвтектической системы. Т6 при Т тройной эвтектики A B C • А+С+Ж А+В+Ж В+С+Ж
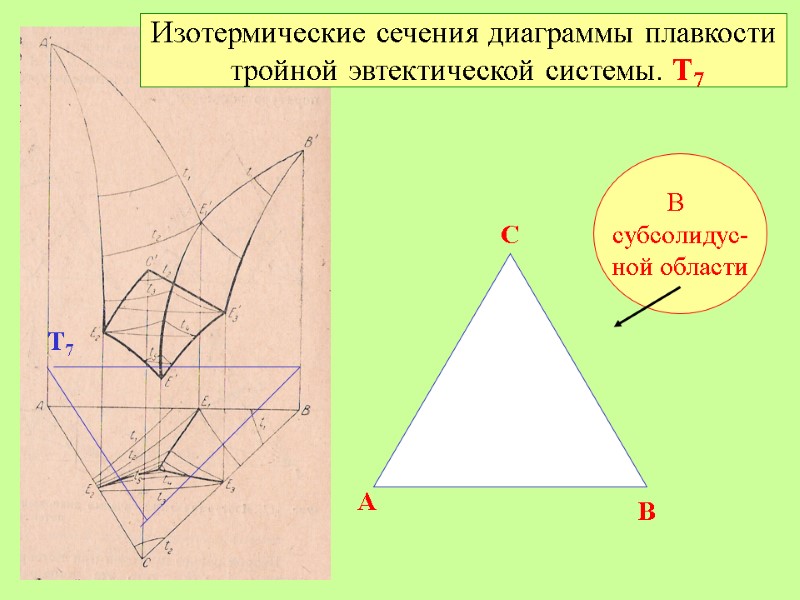
Изотермические сечения диаграммы плавкости тройной эвтектической системы. Т7 В субсолидус- ной области A B C Т7
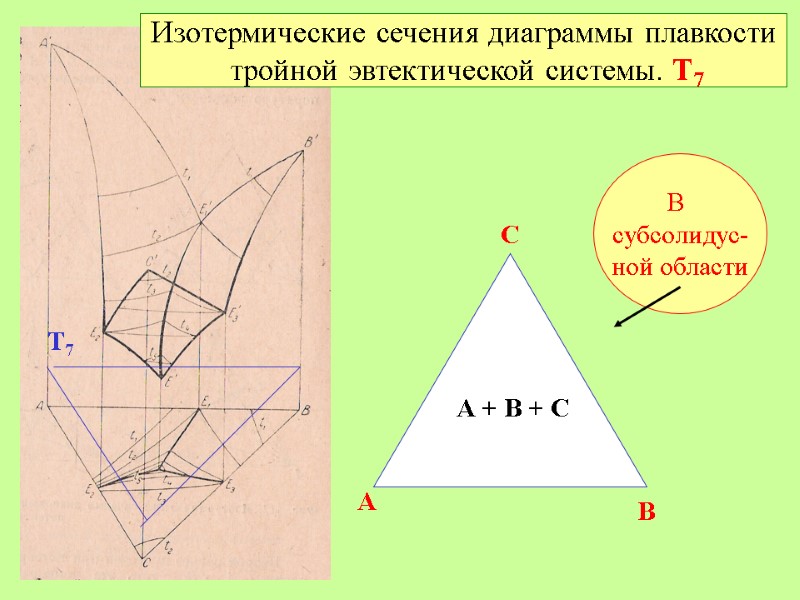
Изотермические сечения диаграммы плавкости тройной эвтектической системы. Т7 В субсолидус- ной области A B C Т7 А + В + С
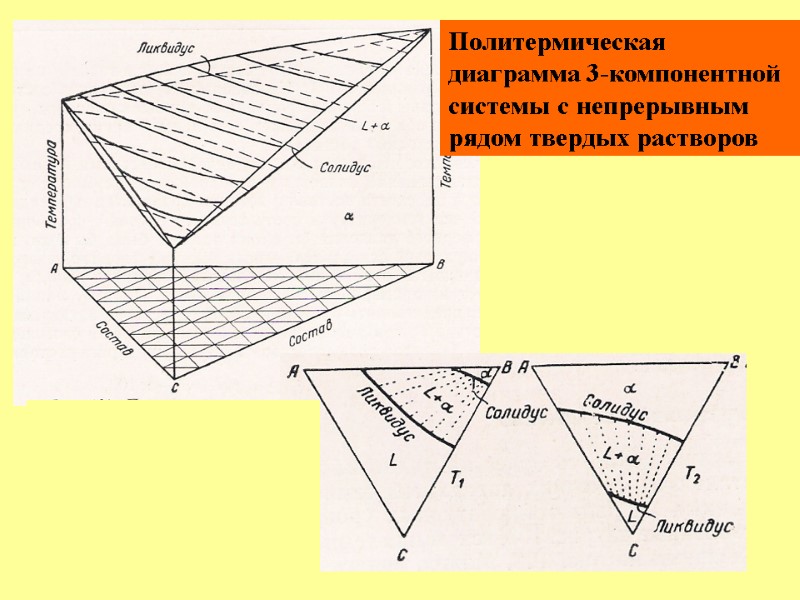
Политермическая диаграмма 3-компонентной системы с непрерывным рядом твердых растворов
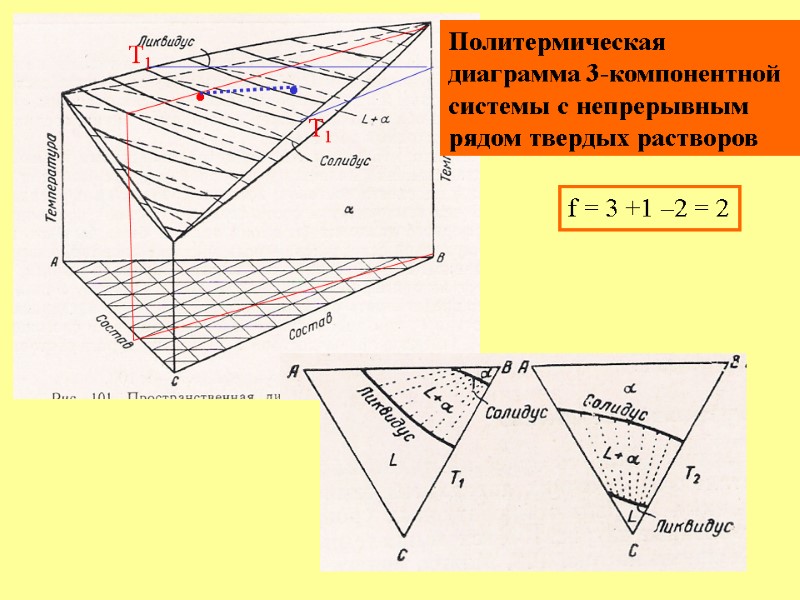
Политермическая диаграмма 3-компонентной системы с непрерывным рядом твердых растворов • • Т1 Т1 f = 3 +1 –2 = 2
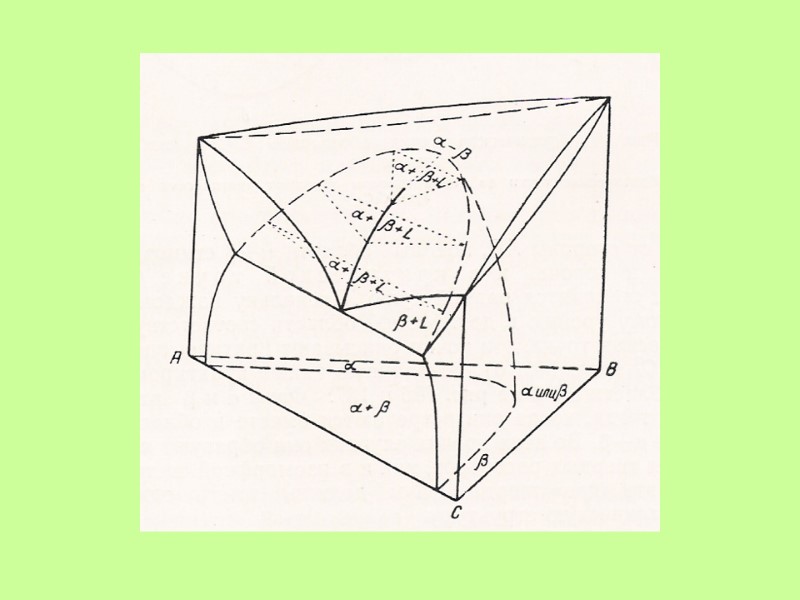
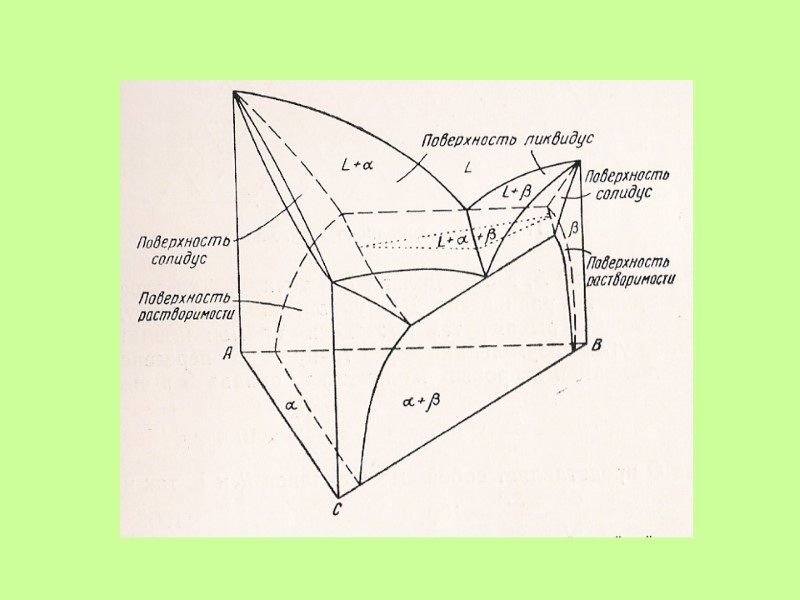
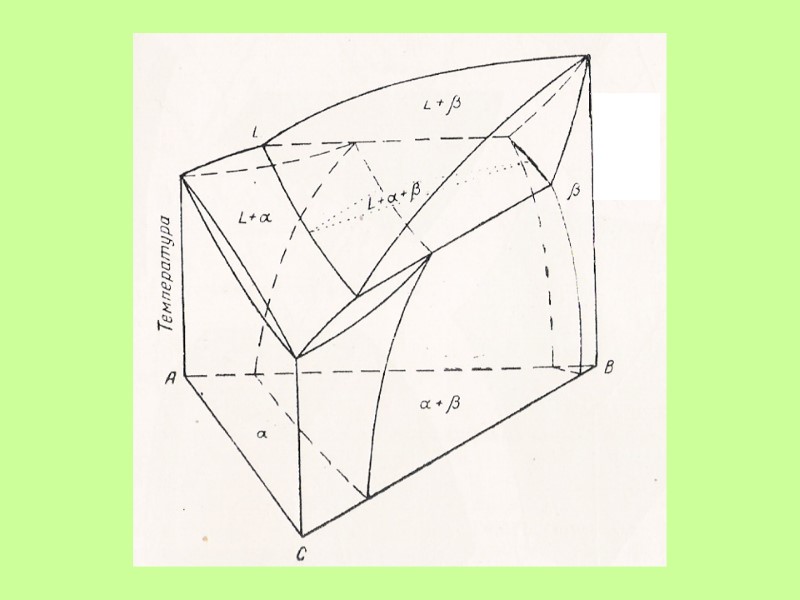
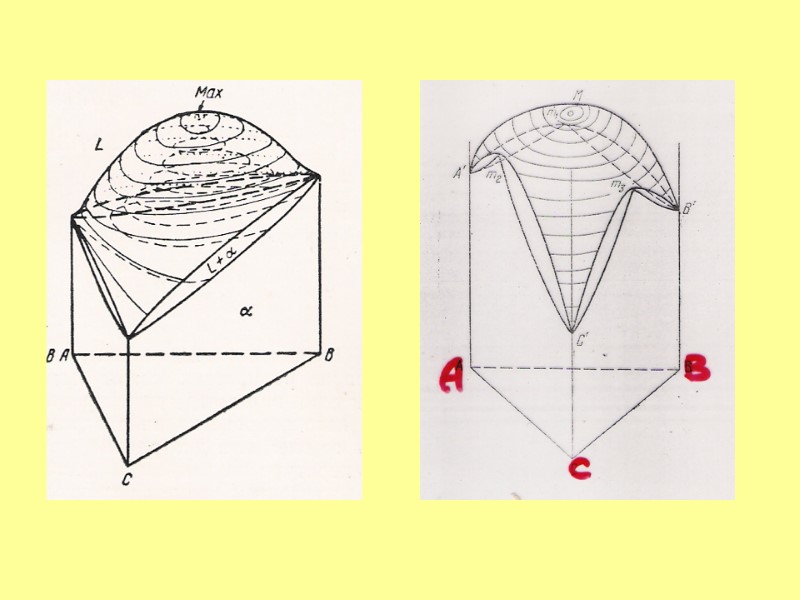

Принцип совместимости: Любые физико-химические системы с меньшим числом компонентов могут совмещаться друг с другом и составлять систему с бóльшим числом компонентов.
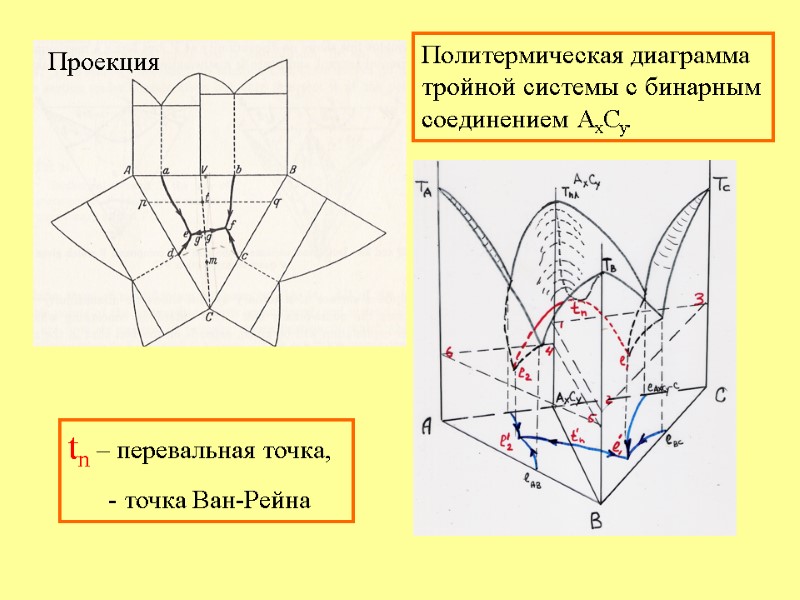
tn – перевальная точка, - точка Ван-Рейна Политермическая диаграмма тройной системы с бинарным соединением АхСу. Проекция
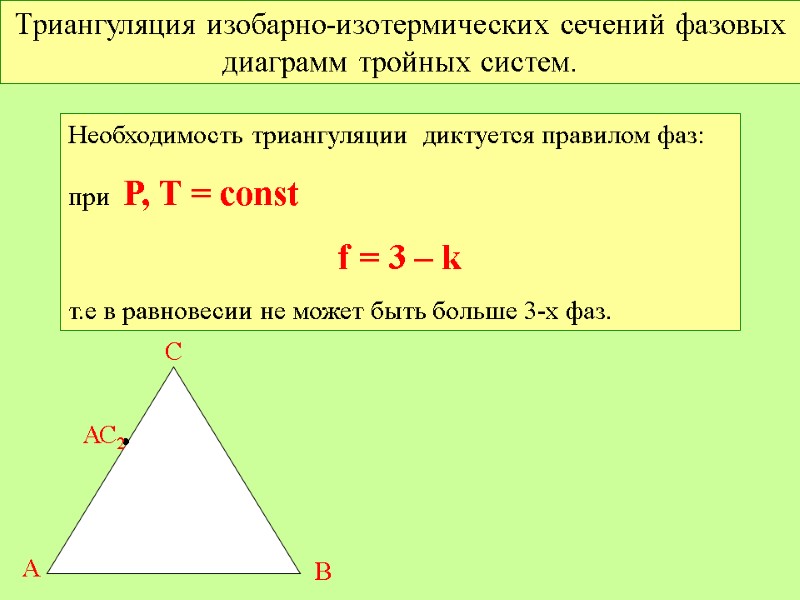
Триангуляция изобарно-изотермических сечений фазовых диаграмм тройных систем. Необходимость триангуляции диктуется правилом фаз: при Р, Т = const f = 3 – k т.е в равновесии не может быть больше 3-х фаз. А В С • АС2
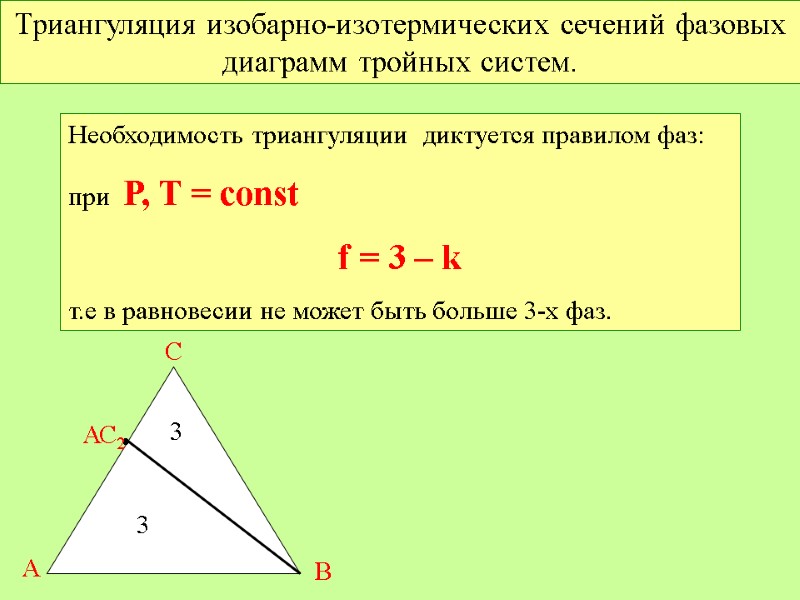
Триангуляция изобарно-изотермических сечений фазовых диаграмм тройных систем. Необходимость триангуляции диктуется правилом фаз: при Р, Т = const f = 3 – k т.е в равновесии не может быть больше 3-х фаз. А В С • АС2 3 3
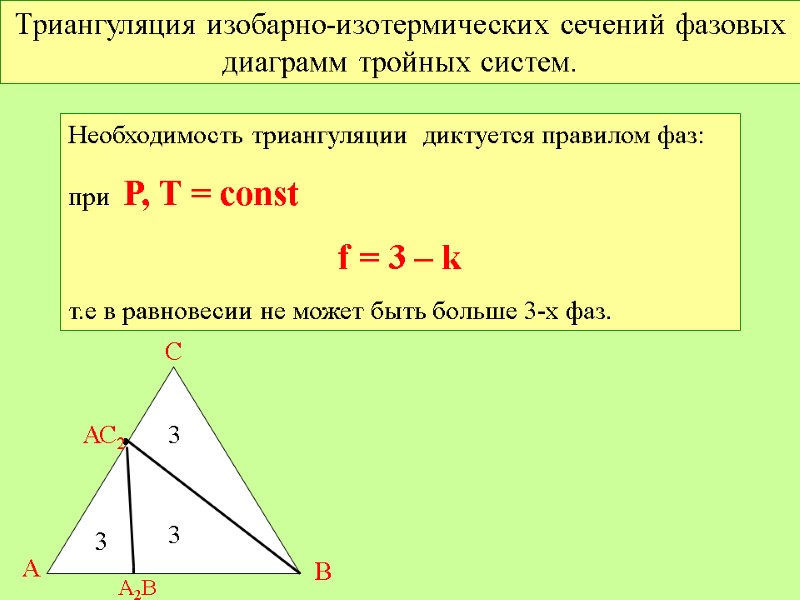
Триангуляция изобарно-изотермических сечений фазовых диаграмм тройных систем. Необходимость триангуляции диктуется правилом фаз: при Р, Т = const f = 3 – k т.е в равновесии не может быть больше 3-х фаз. А В С • АС2 А2В 3 3 3
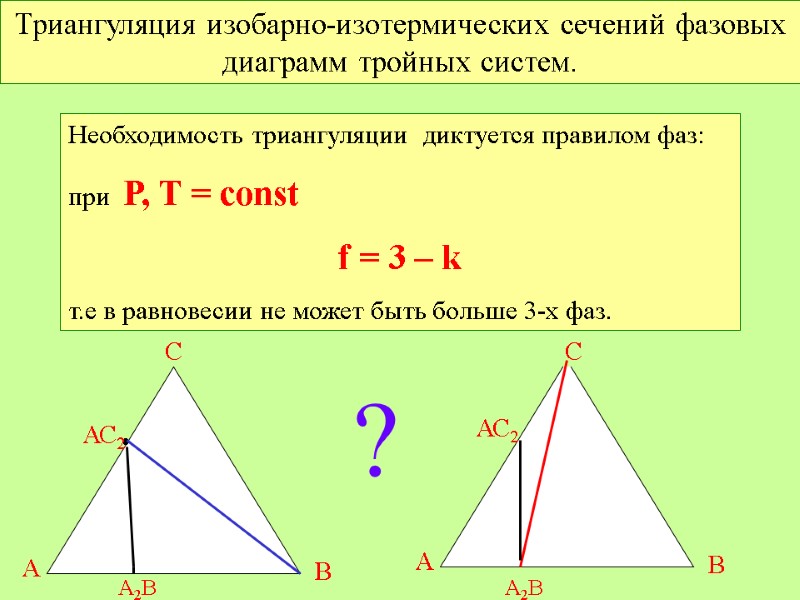
Триангуляция изобарно-изотермических сечений фазовых диаграмм тройных систем. Необходимость триангуляции диктуется правилом фаз: при Р, Т = const f = 3 – k т.е в равновесии не может быть больше 3-х фаз. А В С • АС2 А2В С А В АС2 А2В ?
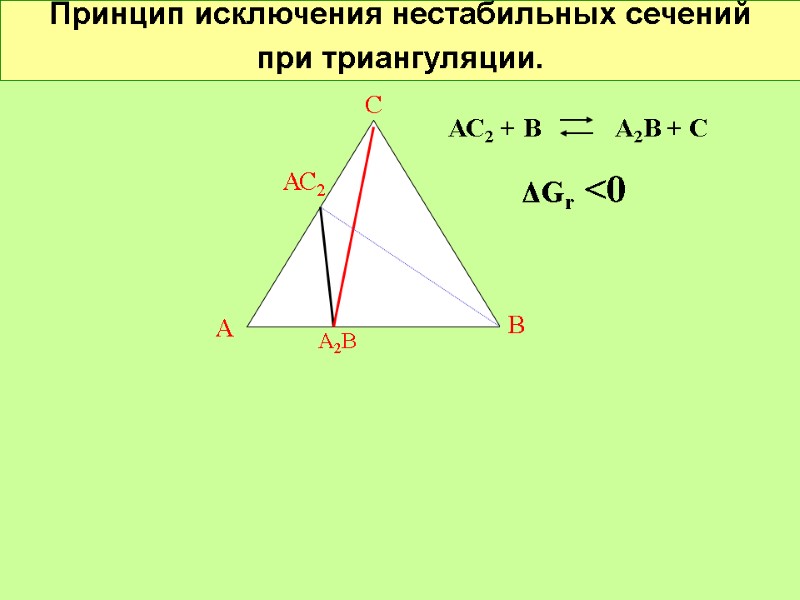
Принцип исключения нестабильных сечений при триангуляции. С А В АС2 А2В АС2 + В А2В + С ΔGr <0
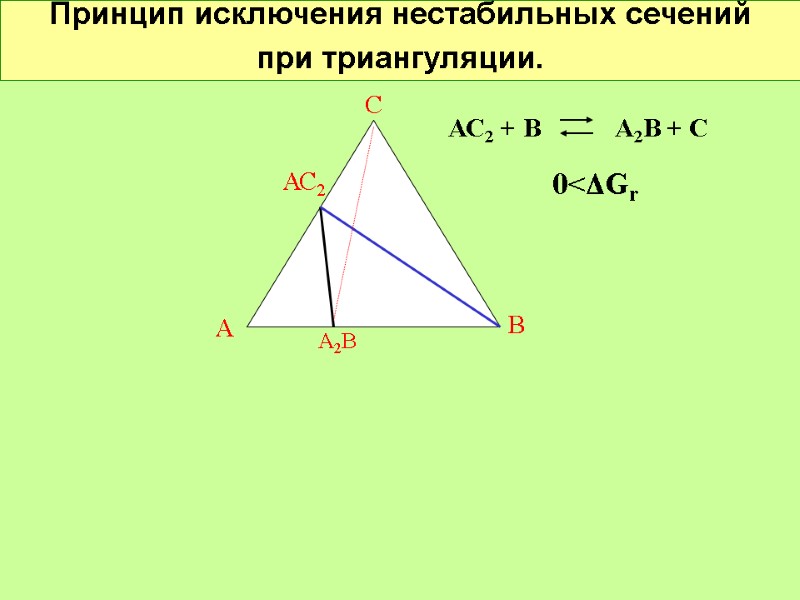
Принцип исключения нестабильных сечений при триангуляции. С А В АС2 А2В АС2 + В А2В + С 0<ΔGr
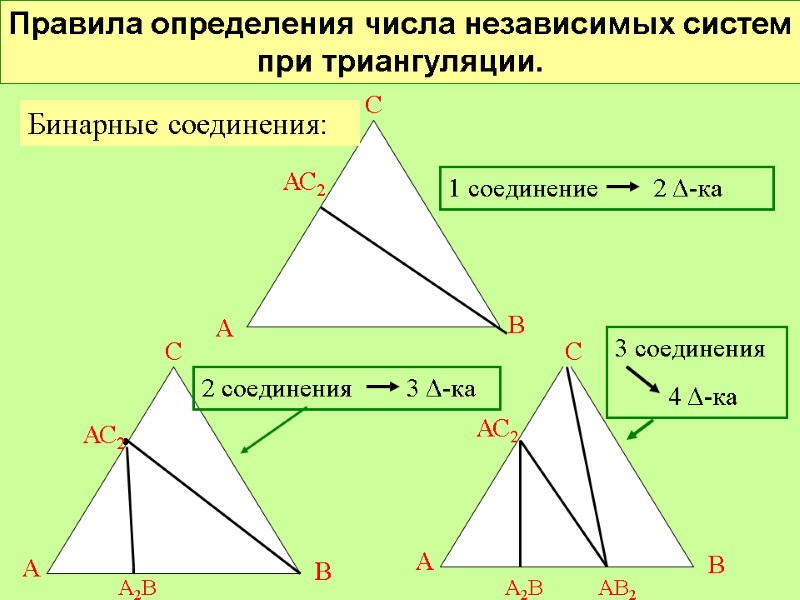
Правила определения числа независимых систем при триангуляции. А В С • АС2 А2В С А В АС2 А2В С А В АС2 Бинарные соединения: 1 соединение 2 Δ-ка 2 соединения 3 Δ-ка АВ2 3 соединения 4 Δ-ка
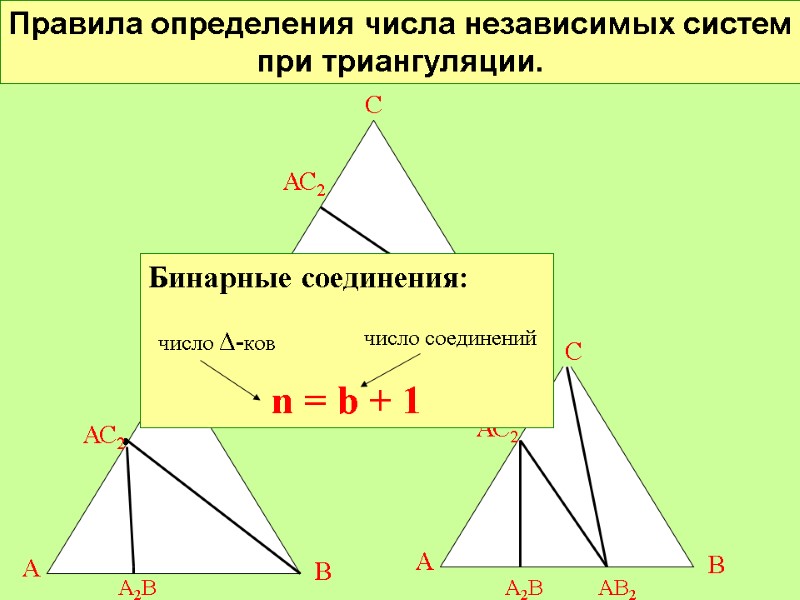
Правила определения числа независимых систем при триангуляции. А В С • АС2 А2В С А В АС2 А2В С А В АС2 Бинарные соединения: n = b + 1 АВ2 число Δ-ков число соединений
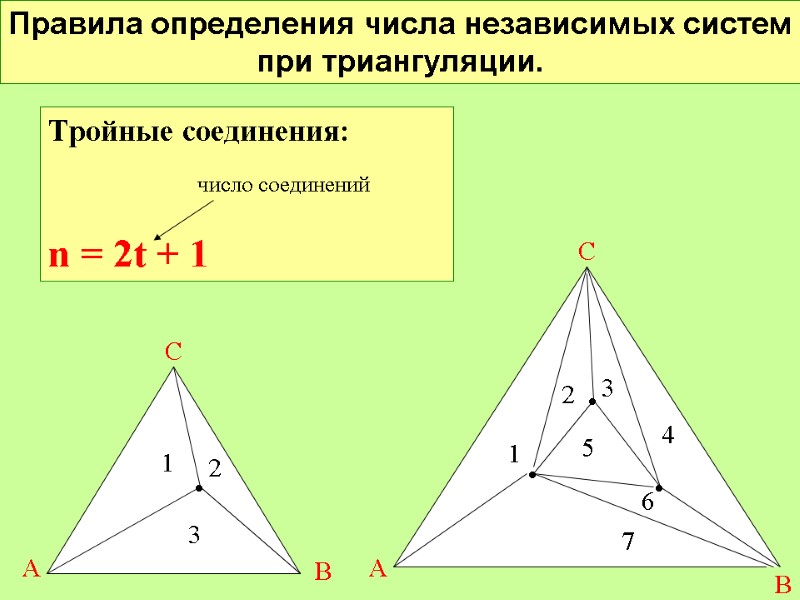
Правила определения числа независимых систем при триангуляции. А В С С А В АС2 Тройные соединения: n = 2t + 1 число соединений • • • • 1 6 5 4 3 2 7 1 2 3
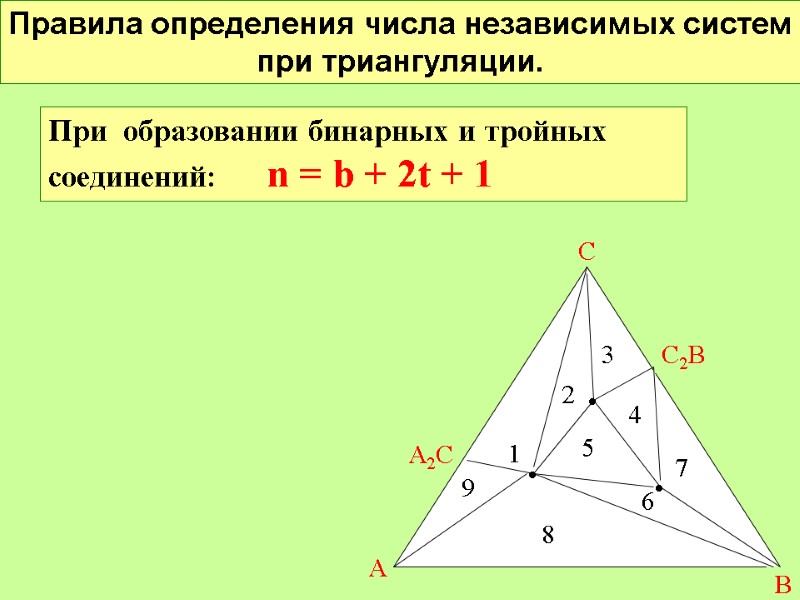
Правила определения числа независимых систем при триангуляции. С А В АС2 При образовании бинарных и тройных соединений: n = b + 2t + 1 • • • 1 6 5 4 3 2 7 A2C C2B 8 9

Триангуляция изобарно-изотермических сечений при образовании бинарных и тройных соединений переменного состава. t b A B C n = b + 2t +1 n = 4
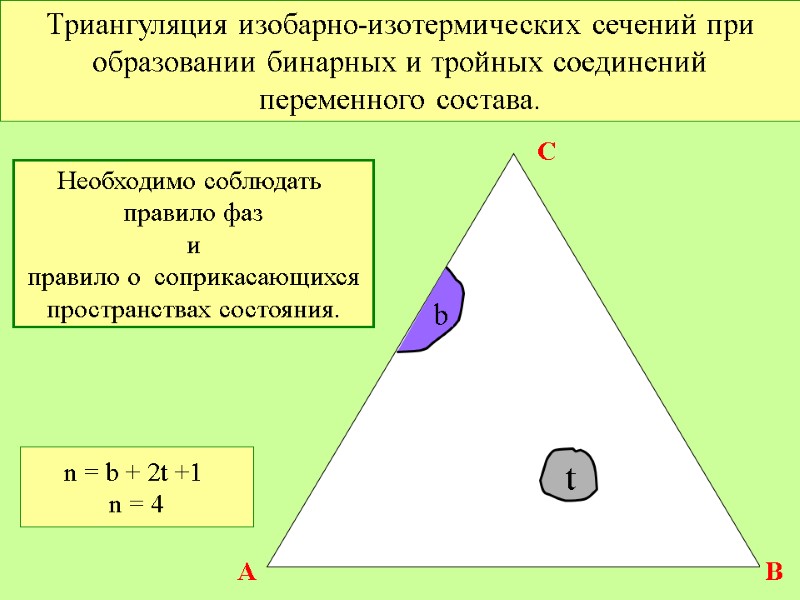
Триангуляция изобарно-изотермических сечений при образовании бинарных и тройных соединений переменного состава. t b A B C n = b + 2t +1 n = 4 Необходимо соблюдать правило фаз и правило о соприкасающихся пространствах состояния. n = b + 2t +1 n = 4
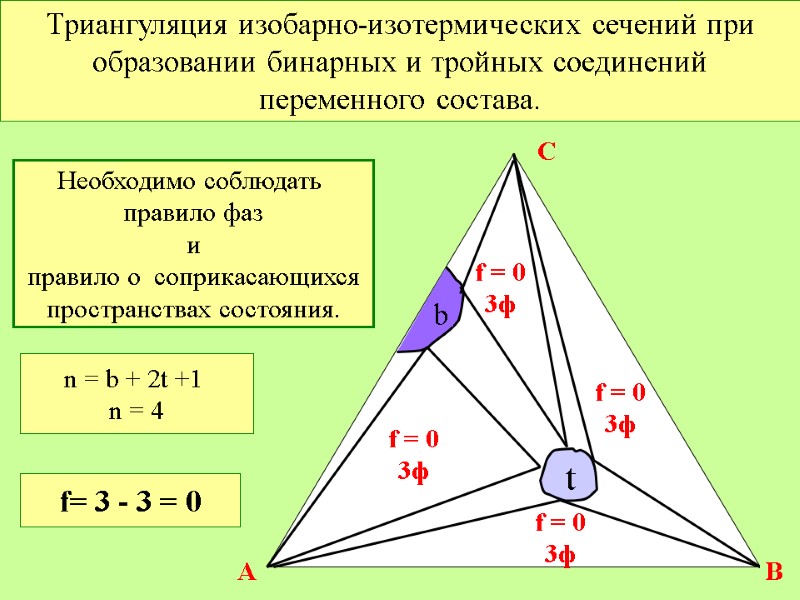
Триангуляция изобарно-изотермических сечений при образовании бинарных и тройных соединений переменного состава. t b Необходимо соблюдать правило фаз и правило о соприкасающихся пространствах состояния. f= 3 - 3 = 0 f = 0 3ф f = 0 3ф f = 0 3ф f = 0 3ф n = b + 2t +1 n = 4 A C B
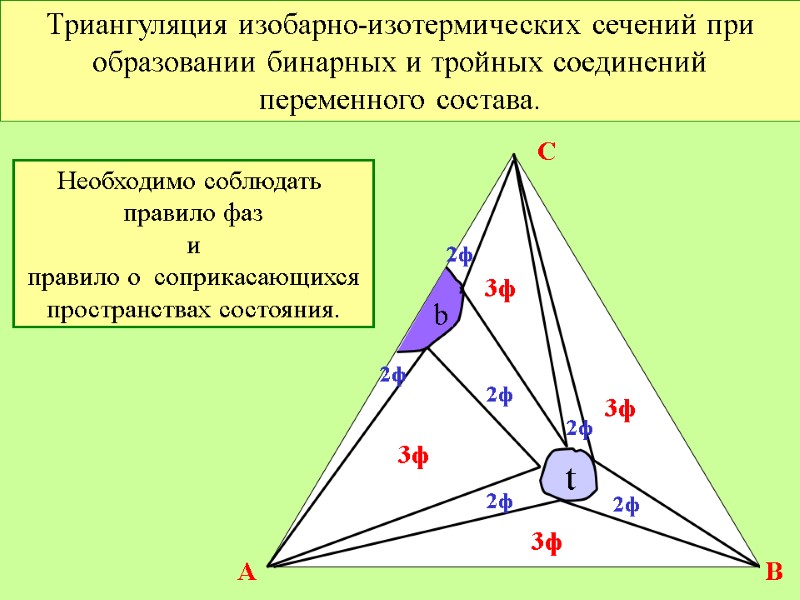
Триангуляция изобарно-изотермических сечений при образовании бинарных и тройных соединений переменного состава. t b Необходимо соблюдать правило фаз и правило о соприкасающихся пространствах состояния. 3ф 3ф 3ф 3ф 2ф 2ф 2ф 2ф 2ф 2ф A C B
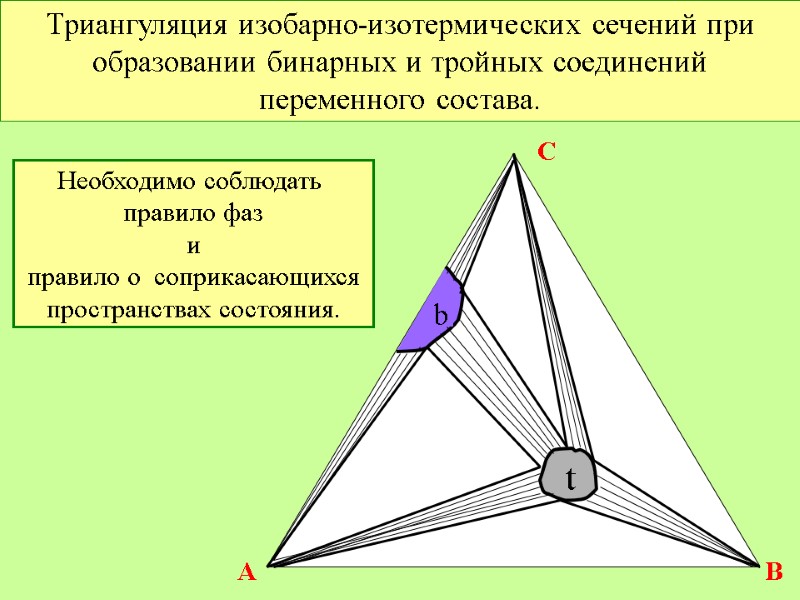
Триангуляция изобарно-изотермических сечений при образовании бинарных и тройных соединений переменного состава. t b Необходимо соблюдать правило фаз и правило о соприкасающихся пространствах состояния. A C B
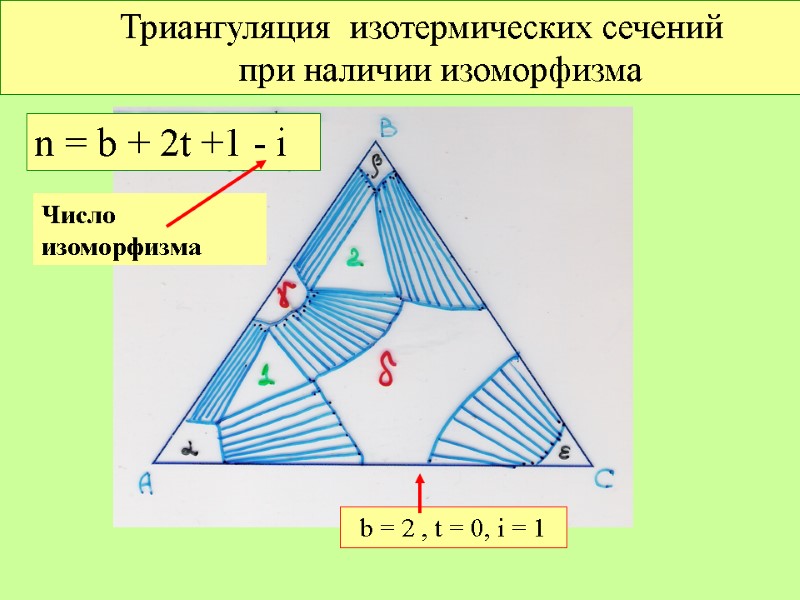
Триангуляция изотермических сечений при наличии изоморфизма n = b + 2t +1 - i Число изоморфизма b = 2 , t = 0, i = 1
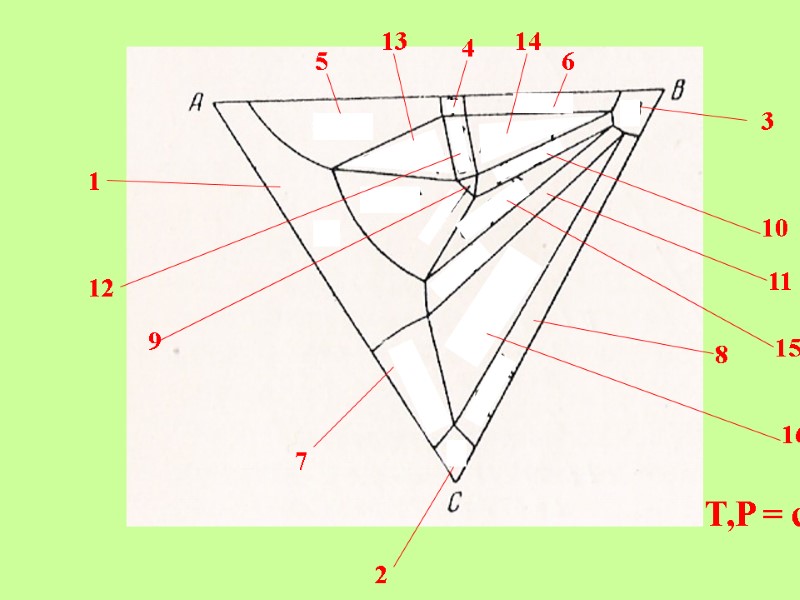
T,P = const 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
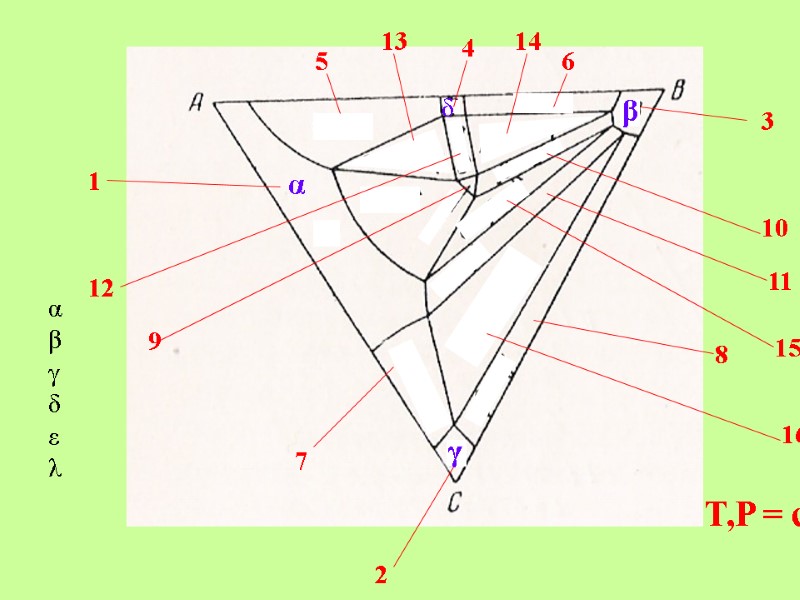
T,P = const 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 αβγδελ α β γ δ
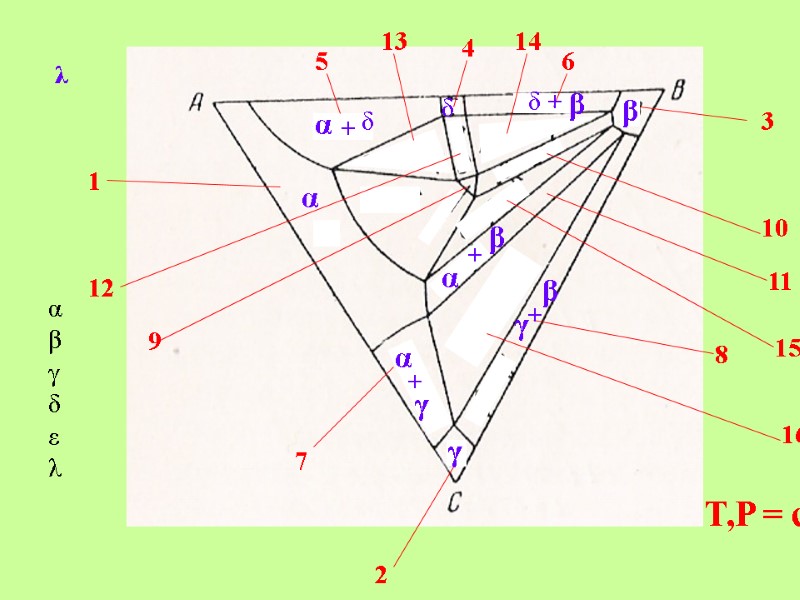
T,P = const 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 αβγδελ α β γ γ β + α + γ δ α δ δ β + + λ α β +
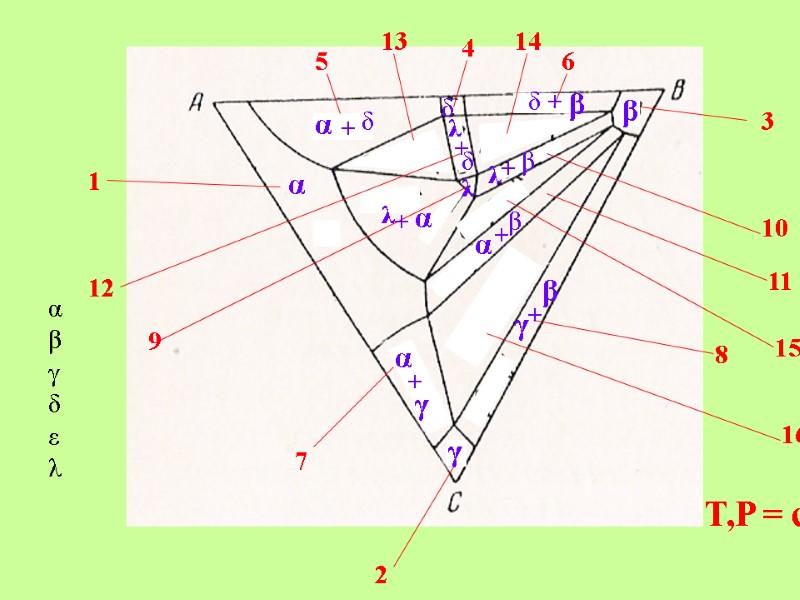
T,P = const 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 αβγδελ α β γ γ β + α + γ δ α δ δ β + + λ λ λ λ α β β α + + + δ +
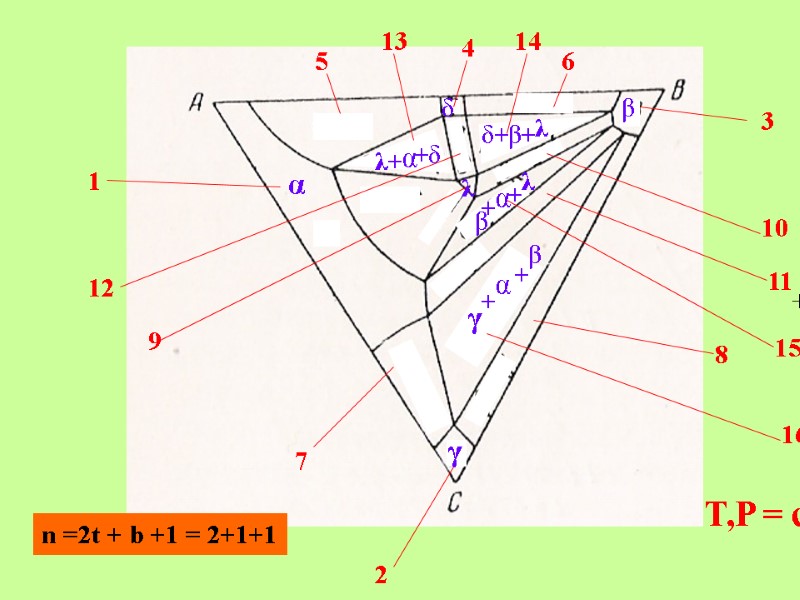
+ T,P = const 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 α β γ δ λ λ α δ δ β λ β α γ β α λ + + + + + + + + n =2t + b +1 = 2+1+1

9568-lecture_-ternary_systems.ppt
- Количество слайдов: 63

