Lecture -Ternary systems.ppt
- Количество слайдов: 63

Избранные главы неорганического материаловедения Лекция 6 Трехкомпонентные (тройные) системы 1. Способы изображения состава. 2. Объемные диаграммы плавкости. 3. Изотермические сечения.
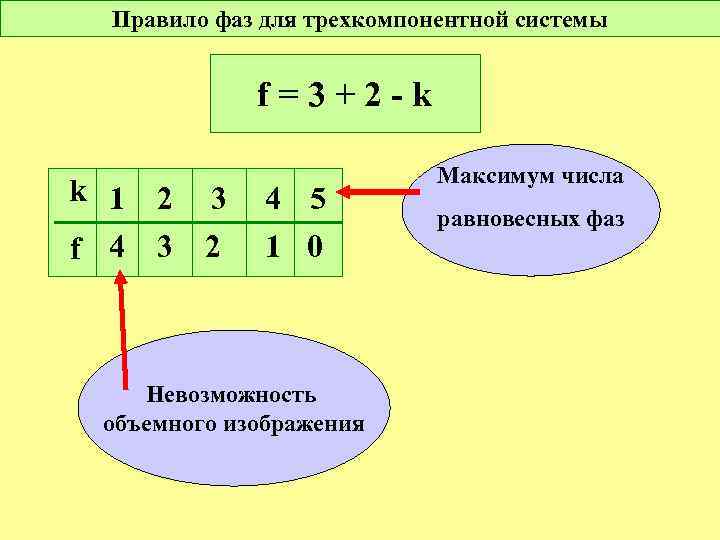
Правило фаз для трехкомпонентной системы f=3+2 -k k 1 f 4 2 3 3 2 4 5 1 0 Невозможность объемного изображения Максимум числа равновесных фаз
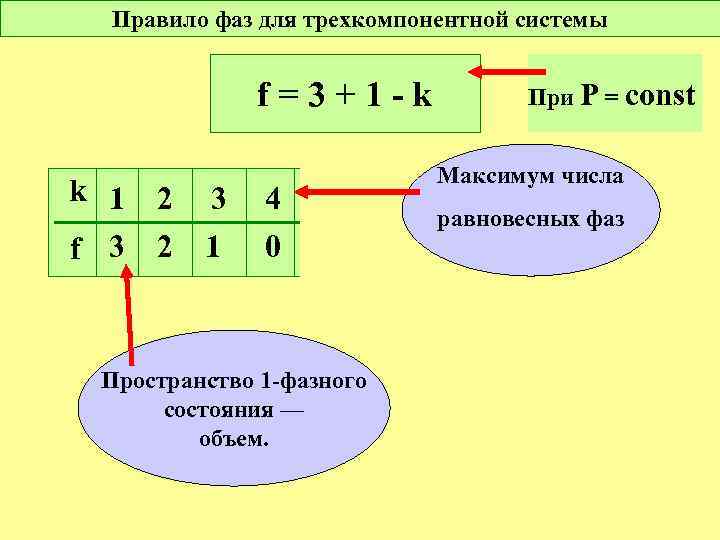
Правило фаз для трехкомпонентной системы f=3+1 -k k 1 f 3 2 2 3 1 4 5 0 0 Пространство 1 -фазного состояния — объем. При Р = const Максимум числа равновесных фаз
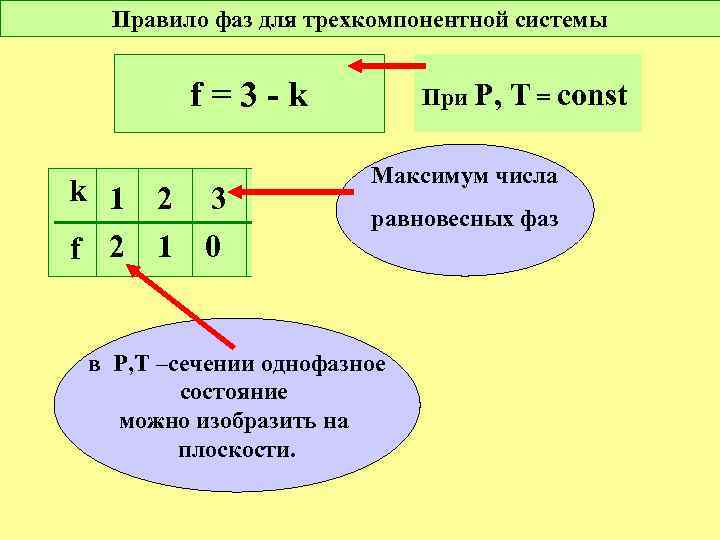
Правило фаз для трехкомпонентной системы f=3 -k k 1 f 2 2 1 3 0 4 5 0 0 При Р, T = const Максимум числа равновесных фаз в Р, Т –сечении однофазное состояние можно изобразить на плоскости.
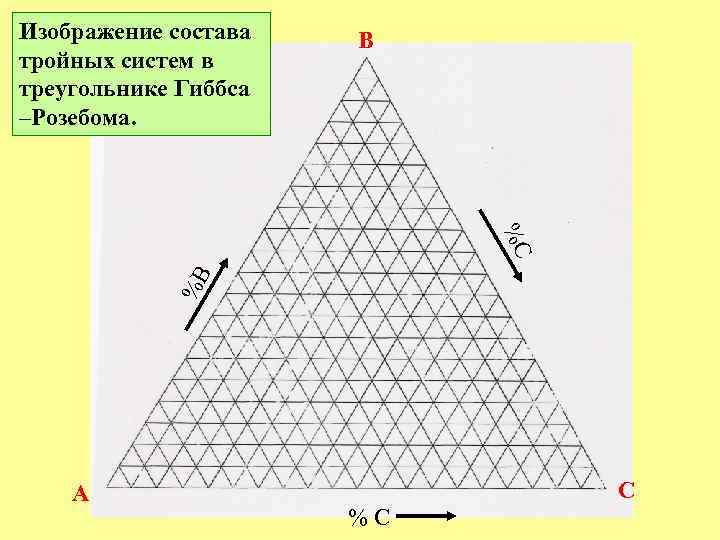
Изображение состава тройных систем в треугольнике Гиббса –Розебома. B %B %C A C %C
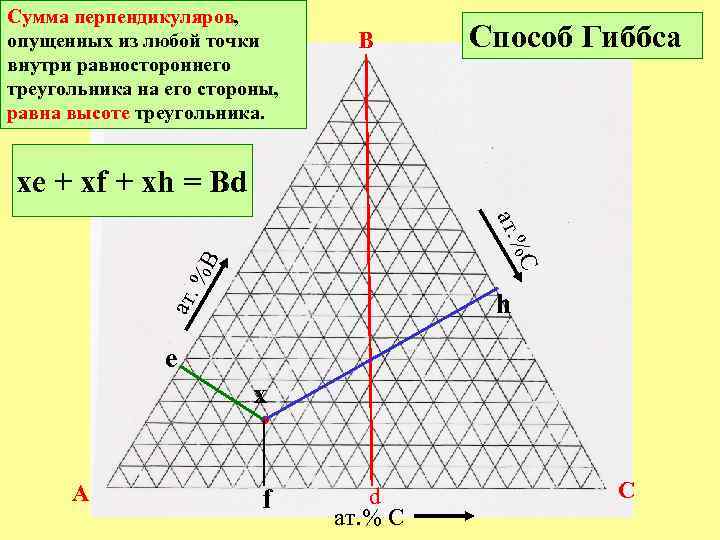
Сумма перпендикуляров, опущенных из любой точки внутри равностороннего треугольника на его стороны, равна высоте треугольника. B Способ Гиббса xe + xf + xh = Bd C %B ат. % ат. h e x • A f d ат. % C C
![Способ Гиббса B x 100 = [A], ат % ат. % C 100% %B Способ Гиббса B x 100 = [A], ат % ат. % C 100% %B](https://present5.com/presentation/1518474_42314580/image-7.jpg)
Способ Гиббса B x 100 = [A], ат % ат. % C 100% %B a x ат. Xa Bd A • C d ат. % C
![Xa Bd Xb x 100 Bd Способ Гиббса B x 100 = [A], ат Xa Bd Xb x 100 Bd Способ Гиббса B x 100 = [A], ат](https://present5.com/presentation/1518474_42314580/image-8.jpg)
Xa Bd Xb x 100 Bd Способ Гиббса B x 100 = [A], ат % = [В], ат % ат. % C 100% %B a ат. x A • d b ат. % C C
![Xa Bd Xb x 100 Bd = [В], ат % x 100 = [С], Xa Bd Xb x 100 Bd = [В], ат % x 100 = [С],](https://present5.com/presentation/1518474_42314580/image-9.jpg)
Xa Bd Xb x 100 Bd = [В], ат % x 100 = [С], ат % ат. % C c 100% %B a x ат. Xc Bd Способ Гиббса B x 100 = [A], ат % A • d b ат. % C C
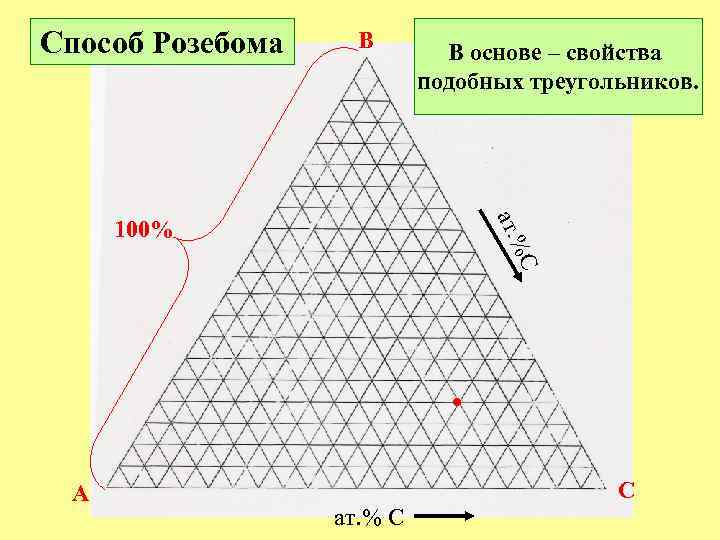
Способ Розебома B В основе – свойства подобных треугольников. C ат. % 100% • A C ат. % C
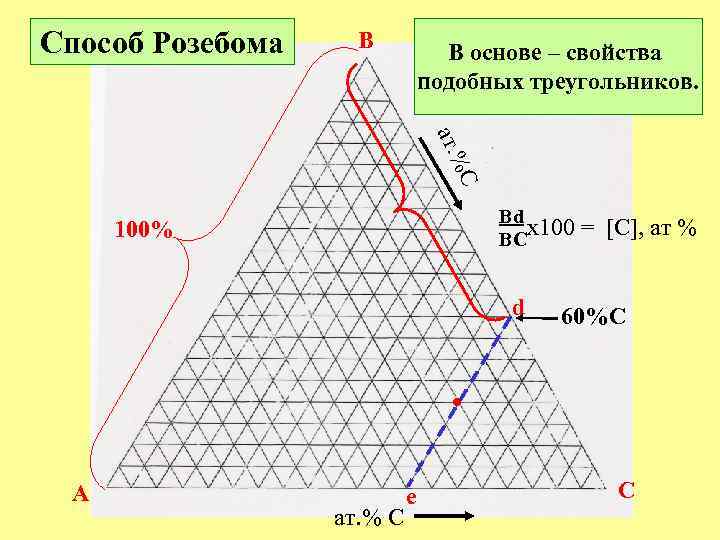
Способ Розебома B В основе – свойства подобных треугольников. C ат. % Bd x 100 BC 100% d = [С], ат % 60%C • A ат. % C e C
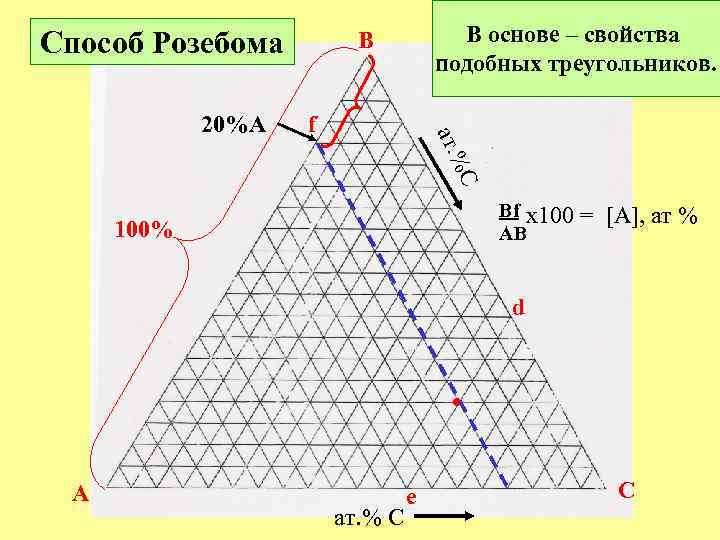
Способ Розебома f C ат. % 20%A В основе – свойства подобных треугольников. B Bf x 100 AB 100% = [A], ат % d • A ат. % C e C
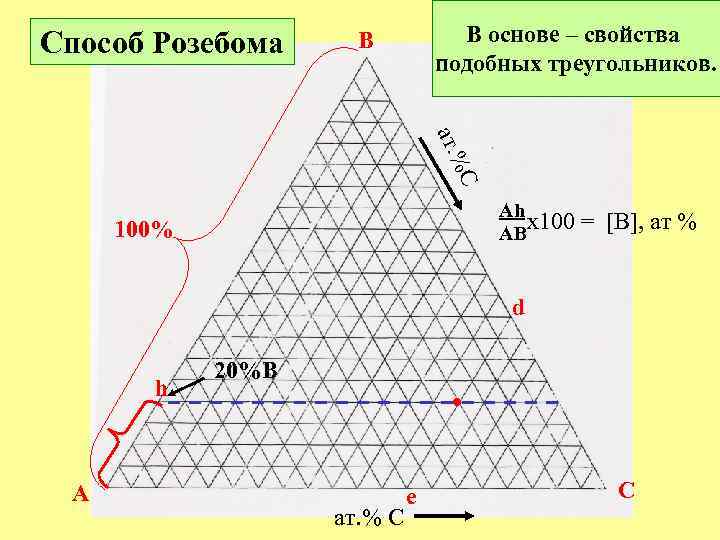
Способ Розебома В основе – свойства подобных треугольников. B C ат. % Ah x 100 AB 100% = [B], ат % d h A 20%B • ат. % C e C
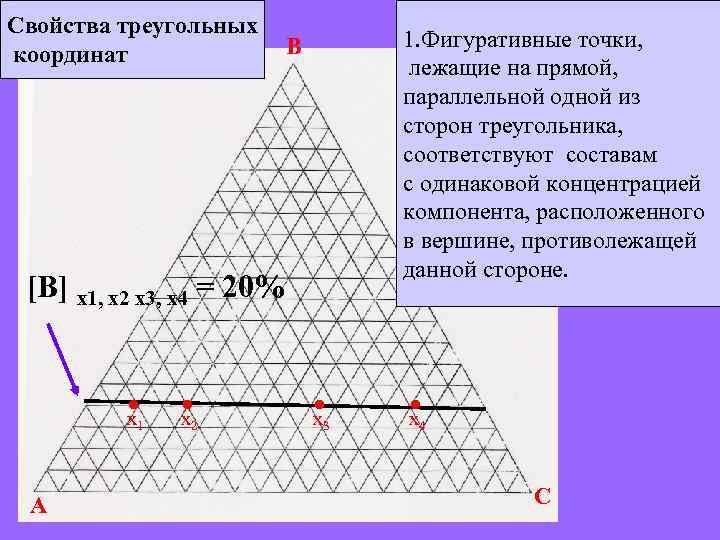
Свойства треугольных координат 1. Фигуративные точки, лежащие на прямой, параллельной одной из сторон треугольника, соответствуют составам с одинаковой концентрацией компонента, расположенного в вершине, противолежащей данной стороне. B [B] x 1, x 2 x 3, x 4 = 20% • х 1 A • х 2 • х 3 • х 4 C
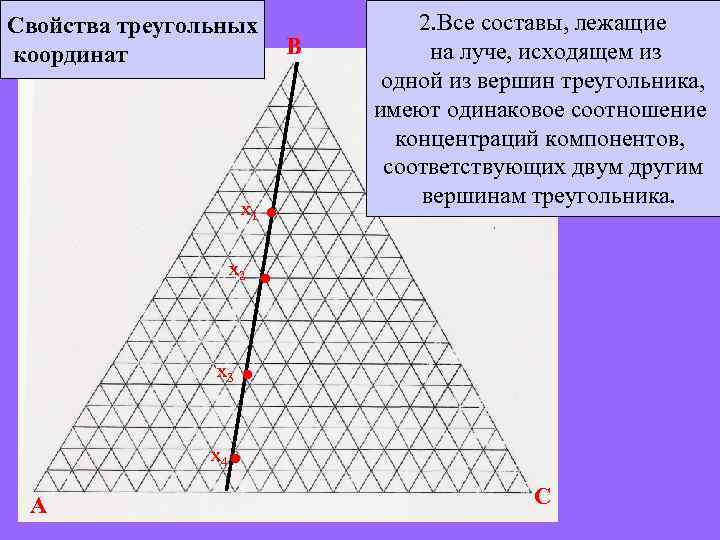
Свойства треугольных координат х1 х2 х3 х4 A B • 2. Все составы, лежащие на луче, исходящем из одной из вершин треугольника, имеют одинаковое соотношение концентраций компонентов, соответствующих двум другим вершинам треугольника. • • • C
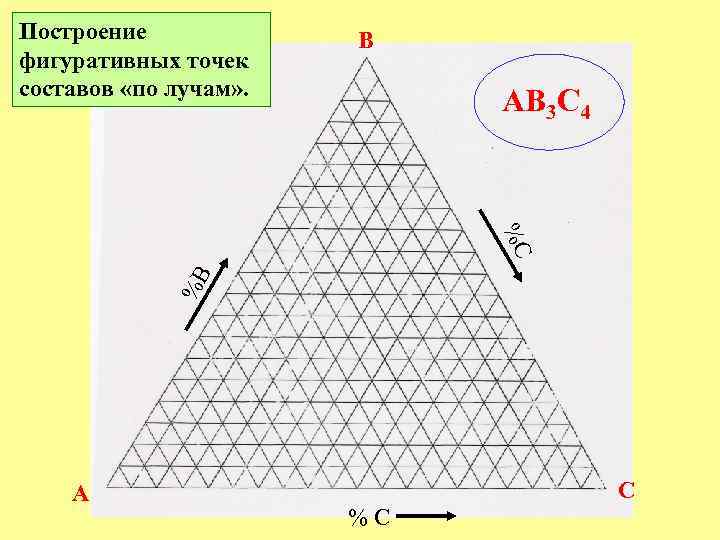
Построение фигуративных точек составов «по лучам» . B АВ 3 С 4 %B %C A C %C
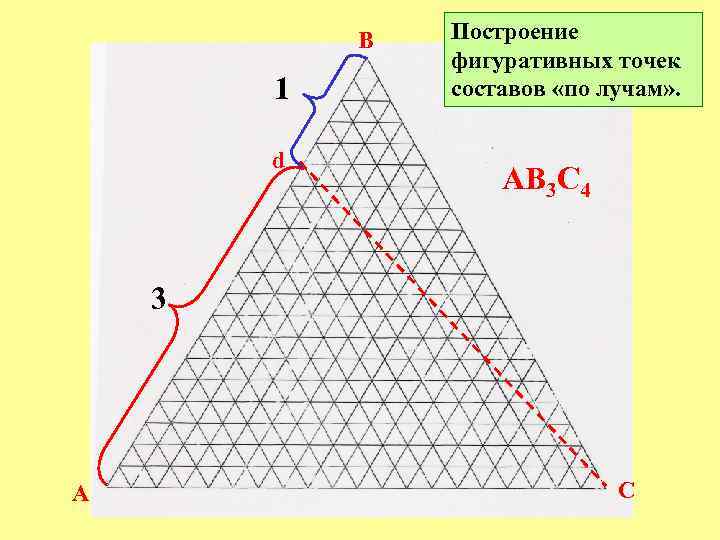
B 1 d Построение фигуративных точек составов «по лучам» . АВ 3 С 4 3 A C
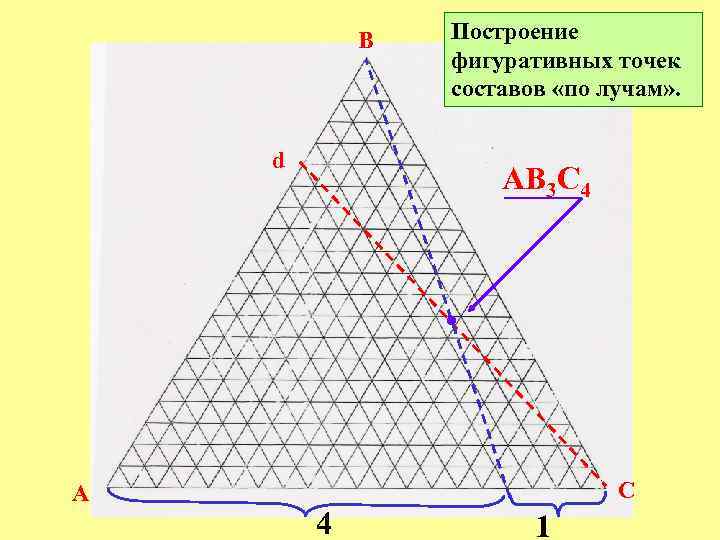
B Построение фигуративных точек составов «по лучам» . d АВ 3 С 4 • A C 4 1
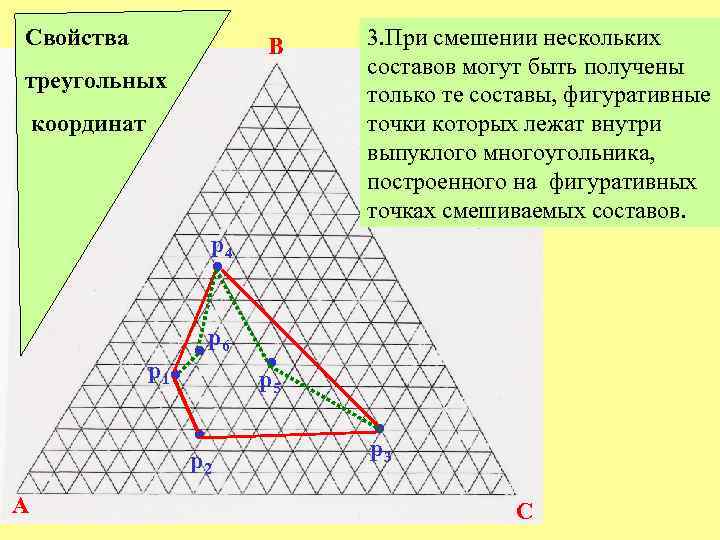
Свойства B треугольных координат 3. При смешении нескольких составов могут быть получены только те составы, фигуративные точки которых лежат внутри выпуклого многоугольника, построенного на фигуративных точках смешиваемых составов. р4 • р1 • • • р6 р2 A • р5 • р3 C
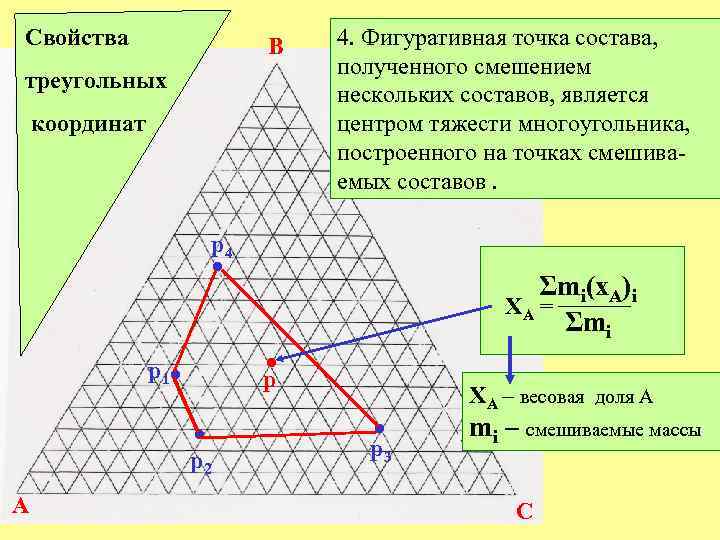
Свойства B треугольных координат 4. Фигуративная точка состава, полученного смешением нескольких составов, является центром тяжести многоугольника, построенного на точках смешиваемых составов. р4 • • р1 • р2 A Σmi(x. A)i ХА = Σmi • р ХА – весовая доля А mi – смешиваемые массы 3 C
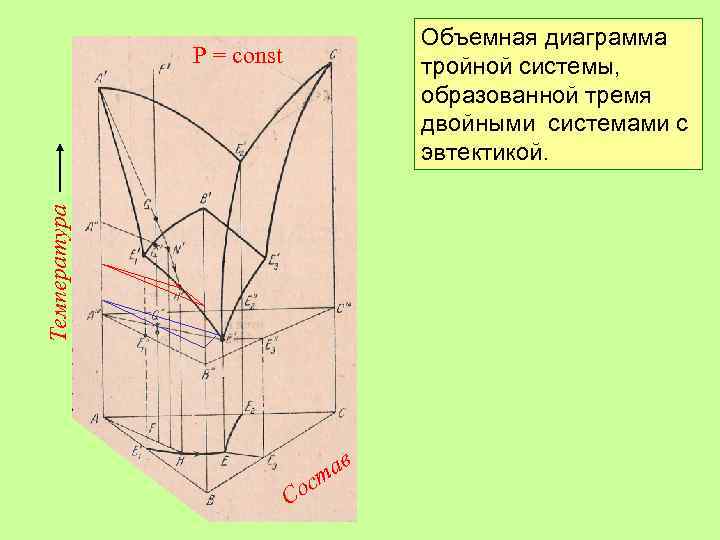
Объемная диаграмма тройной системы, образованной тремя двойными системами с эвтектикой. Температура Р = const Со ав ст
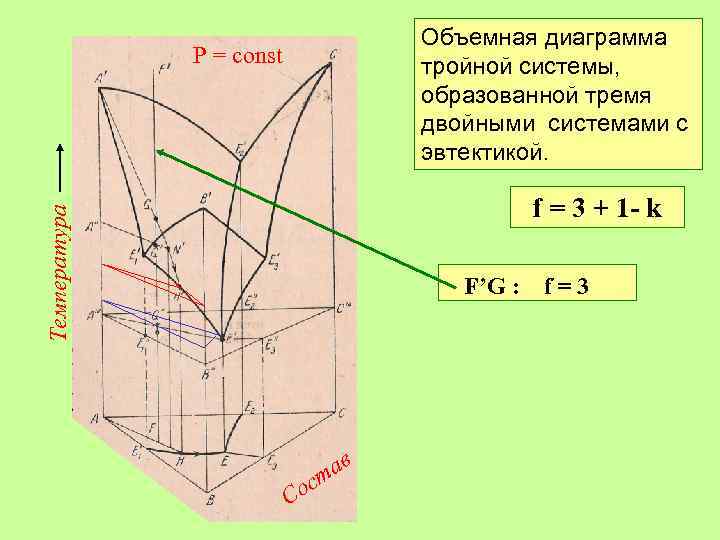
Объемная диаграмма тройной системы, образованной тремя двойными системами с эвтектикой. Р = const Температура f = 3 + 1 - k F’G : f = 3 GH’ : f = 2 H’E’: f = 1 E’: f=0 Со ав ст
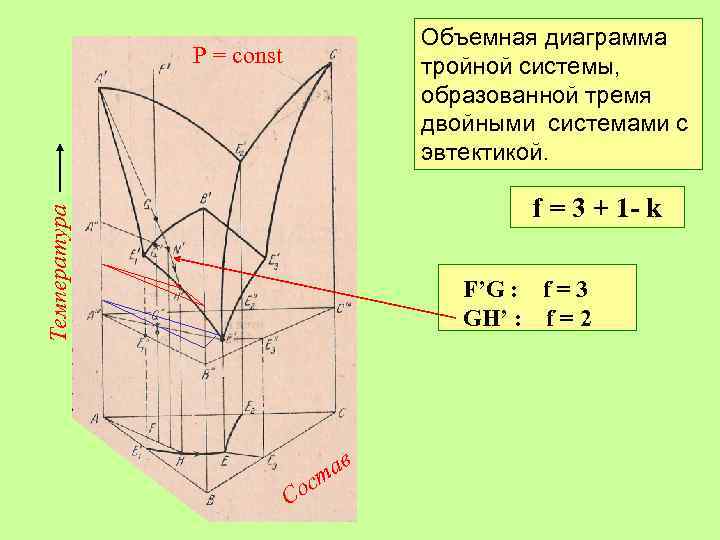
Объемная диаграмма тройной системы, образованной тремя двойными системами с эвтектикой. Р = const Температура f = 3 + 1 - k F’G : f = 3 GH’ : f = 2 H’E’: f = 1 E’: f=0 Со ав ст
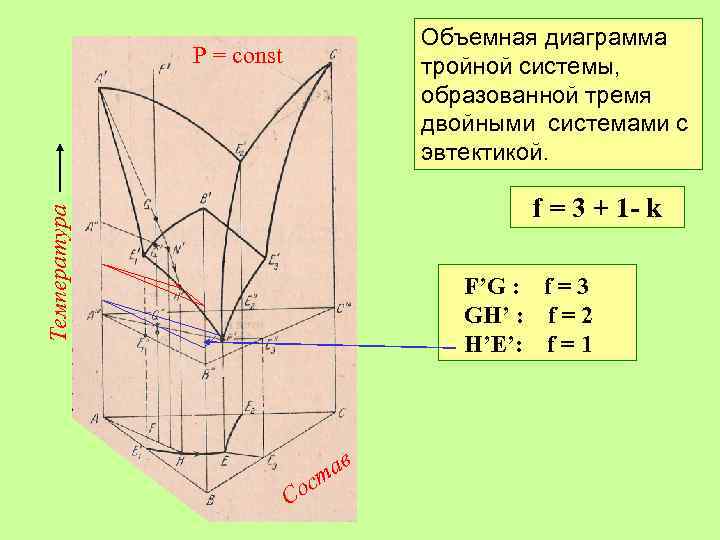
Объемная диаграмма тройной системы, образованной тремя двойными системами с эвтектикой. Р = const Температура f = 3 + 1 - k F’G : f = 3 GH’ : f = 2 H’E’: f = 1 E’: f=0 Со ав ст
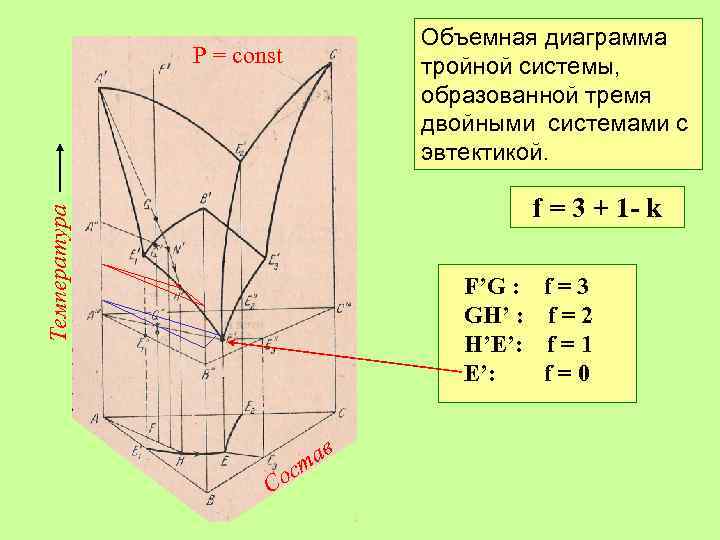
Объемная диаграмма тройной системы, образованной тремя двойными системами с эвтектикой. Р = const Температура f = 3 + 1 - k F’G : f = 3 GH’ : f = 2 H’E’: f = 1 E’: f=0 Со ав ст
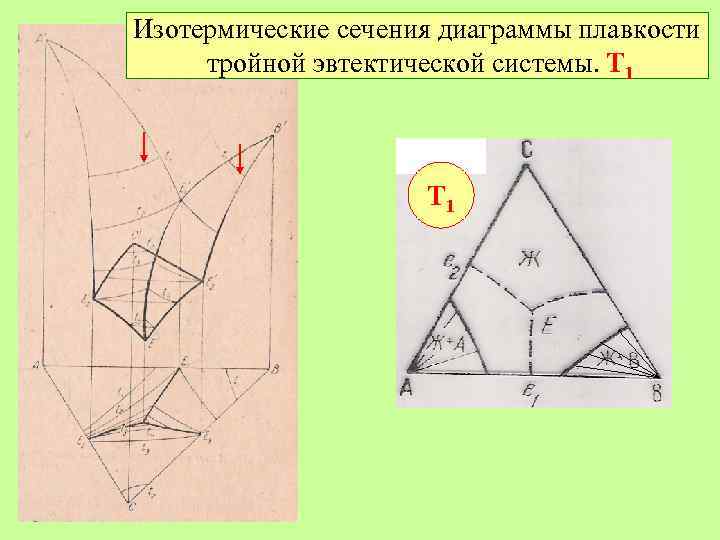
Изотермические сечения диаграммы плавкости тройной эвтектической системы. Т 1
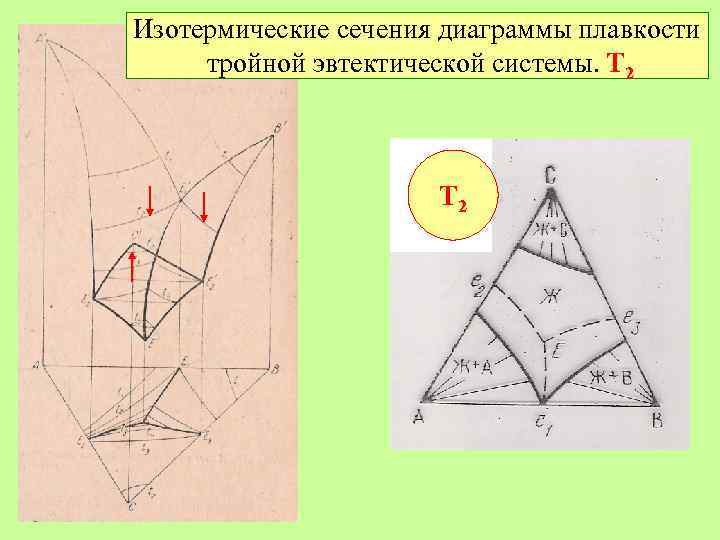
Изотермические сечения диаграммы плавкости тройной эвтектической системы. Т 2
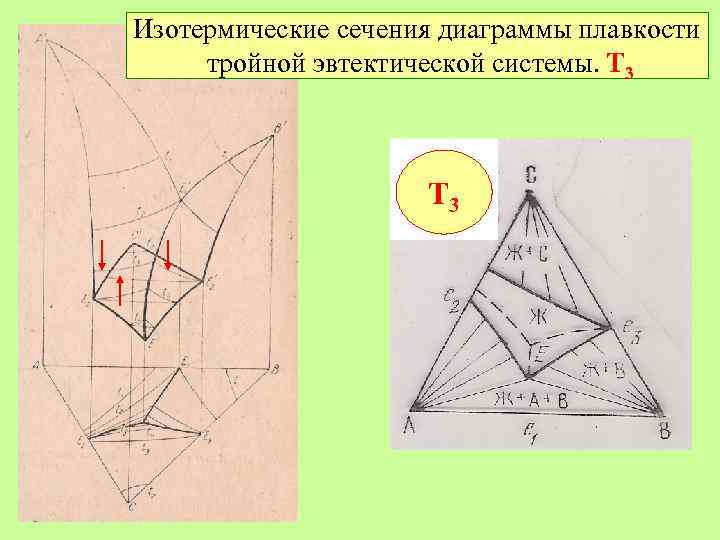
Изотермические сечения диаграммы плавкости тройной эвтектической системы. Т 3
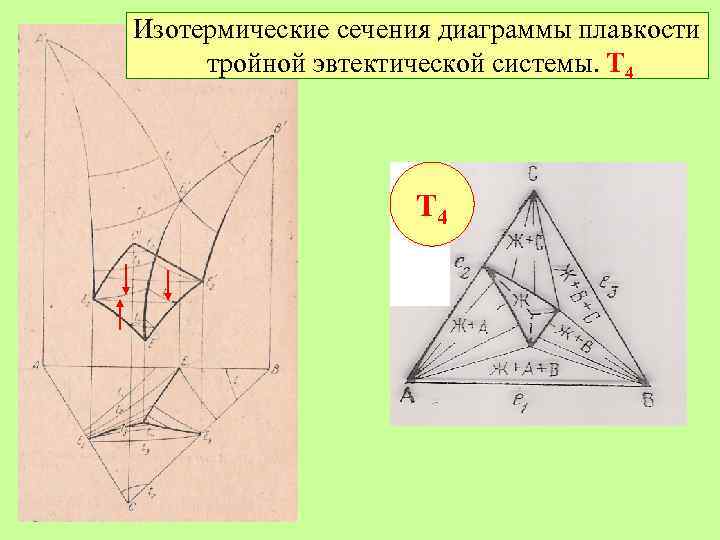
Изотермические сечения диаграммы плавкости тройной эвтектической системы. Т 4
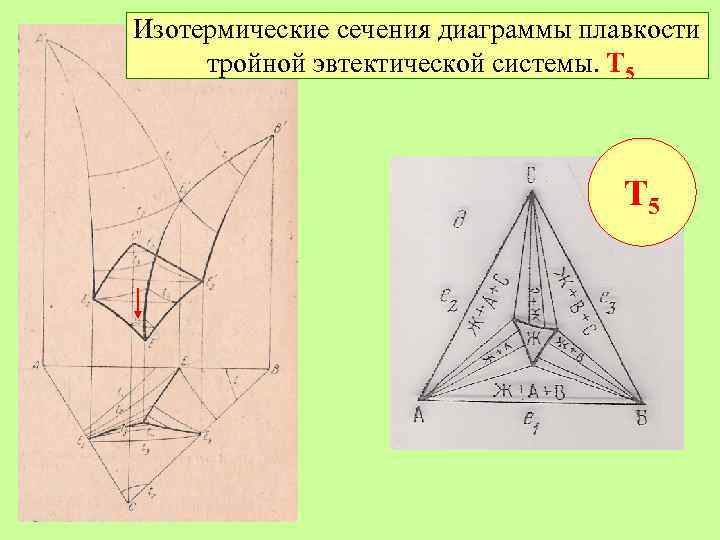
Изотермические сечения диаграммы плавкости тройной эвтектической системы. Т 5
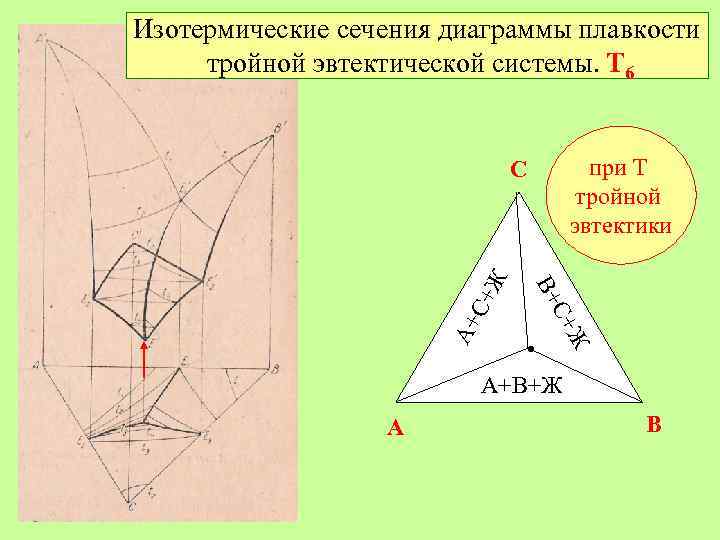
Изотермические сечения диаграммы плавкости тройной эвтектической системы. Т 6 при Т тройной эвтектики А+ С+ Ж С+ В+ Ж C • А+В+Ж A B
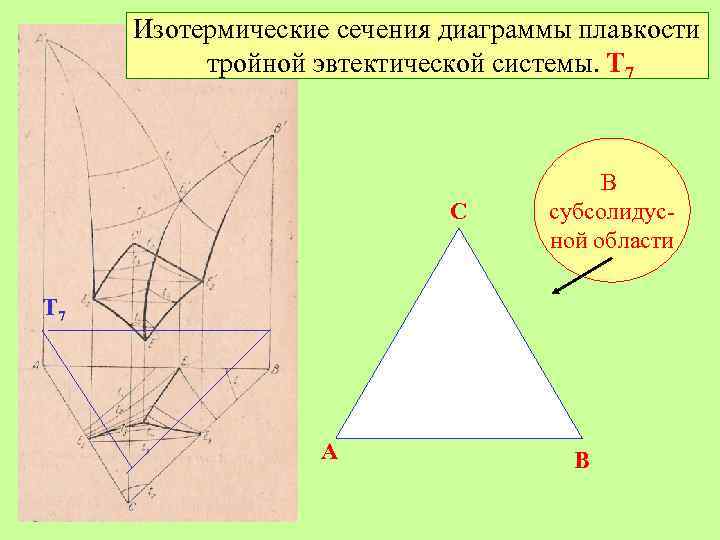
Изотермические сечения диаграммы плавкости тройной эвтектической системы. Т 7 C В субсолидусной области Т 7 A B
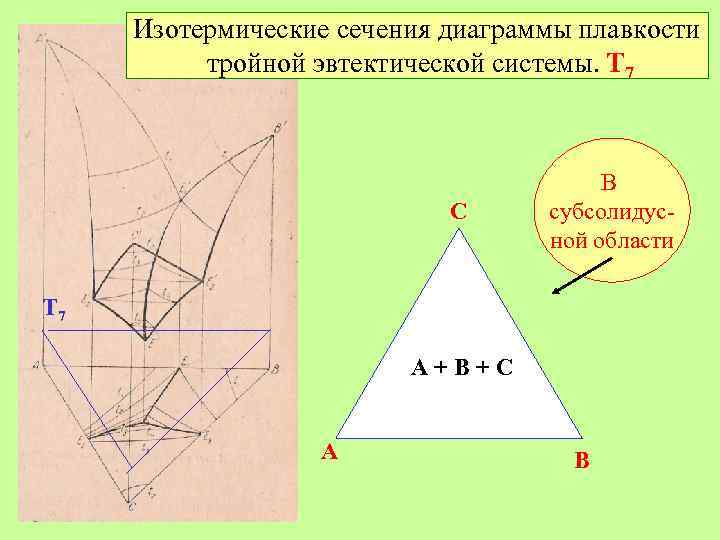
Изотермические сечения диаграммы плавкости тройной эвтектической системы. Т 7 C В субсолидусной области Т 7 А+В+С A B
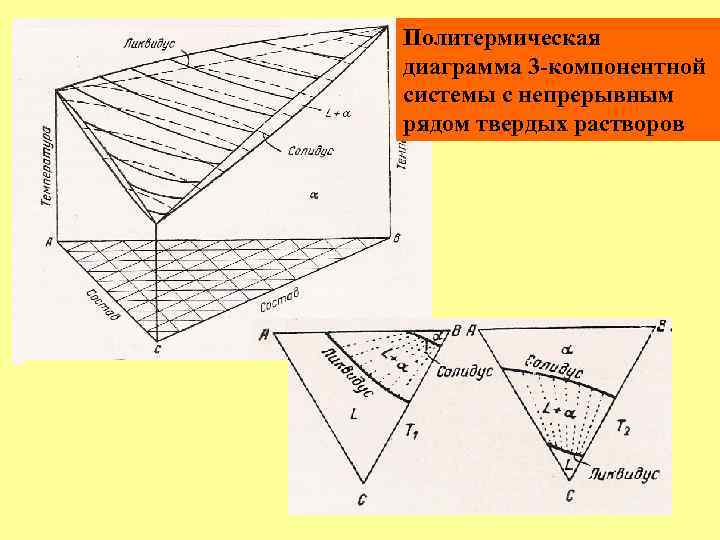
Политермическая диаграмма 3 -компонентной системы с непрерывным рядом твердых растворов
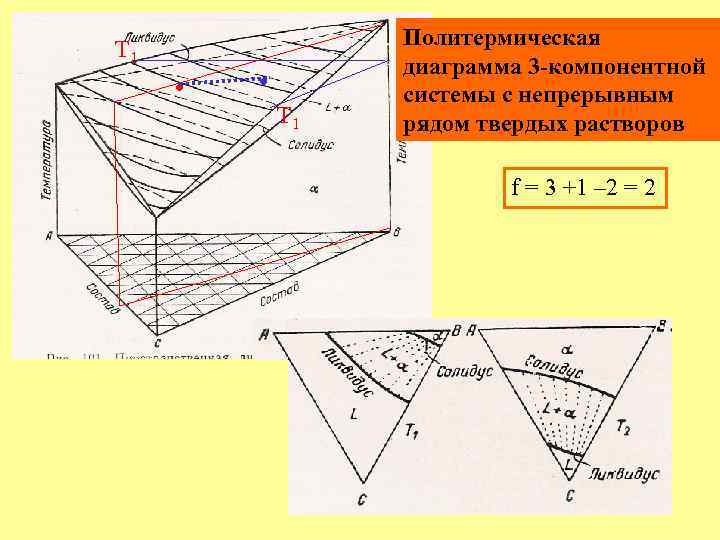
Т 1 • • Т 1 Политермическая диаграмма 3 -компонентной системы с непрерывным рядом твердых растворов f = 3 +1 – 2 = 2
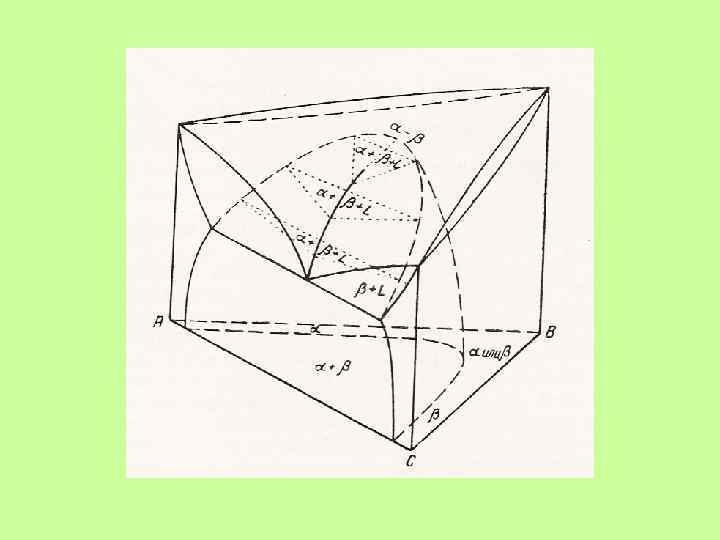
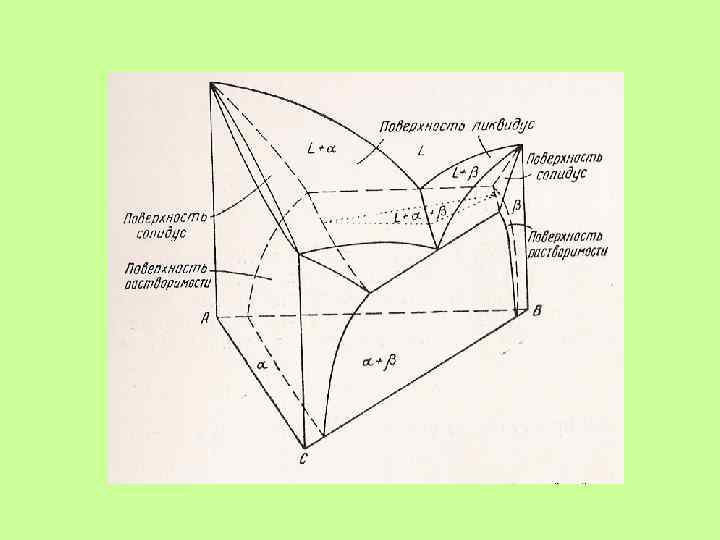
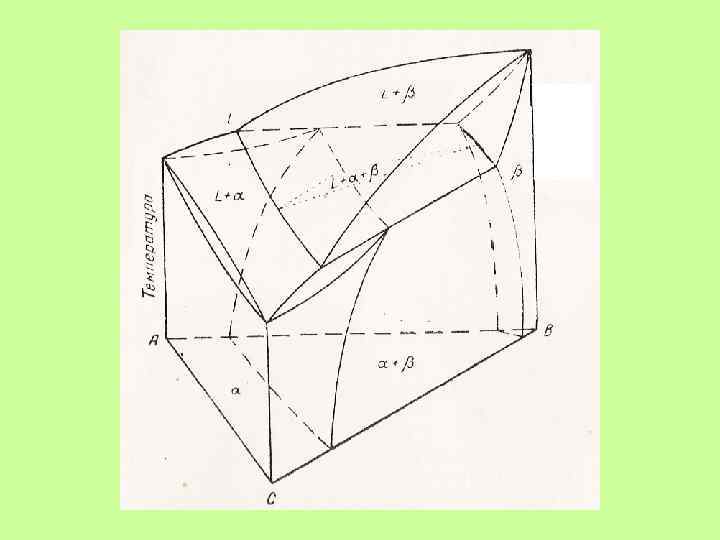
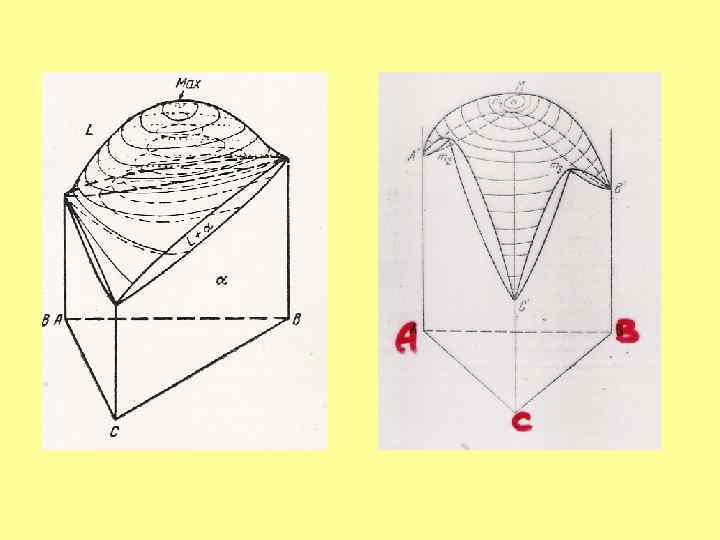

Принцип совместимости: Любые физико-химические системы с меньшим числом компонентов могут совмещаться друг с другом и составлять систему с бóльшим числом компонентов.
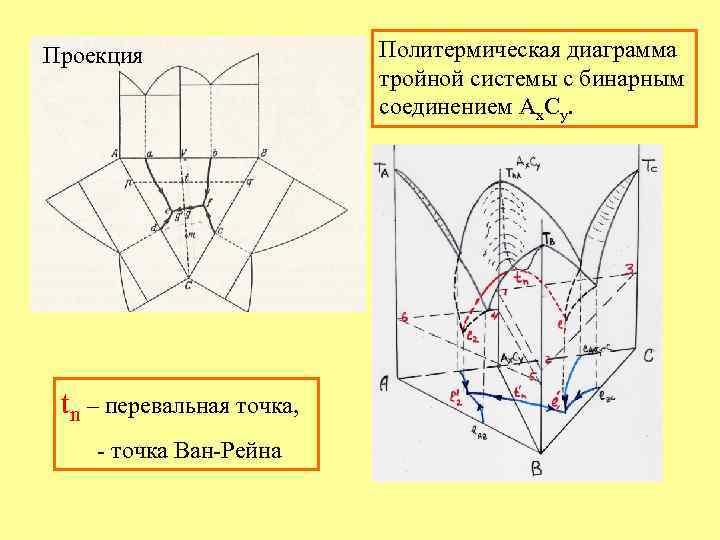
Проекция tn – перевальная точка, - точка Ван-Рейна Политермическая диаграмма тройной системы с бинарным соединением Ах. Су.
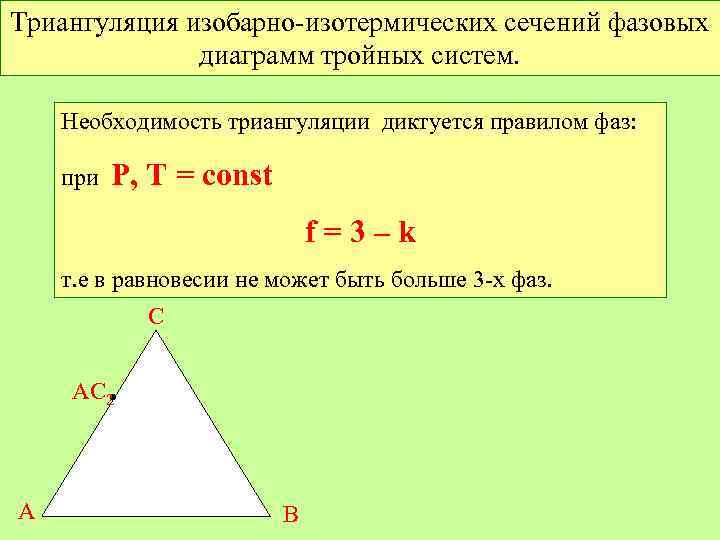
Триангуляция изобарно-изотермических сечений фазовых диаграмм тройных систем. Необходимость триангуляции диктуется правилом фаз: при Р, Т = const f=3–k т. е в равновесии не может быть больше 3 -х фаз. С АС 2 • А В
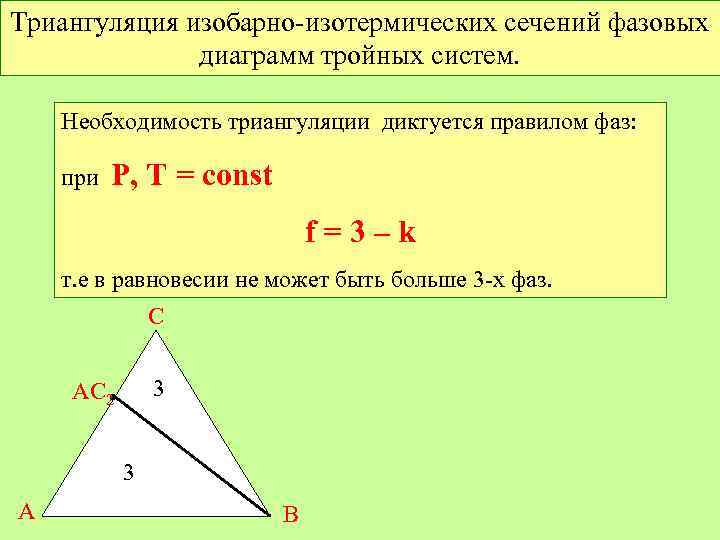
Триангуляция изобарно-изотермических сечений фазовых диаграмм тройных систем. Необходимость триангуляции диктуется правилом фаз: при Р, Т = const f=3–k т. е в равновесии не может быть больше 3 -х фаз. С 3 АС 2 • 3 А В
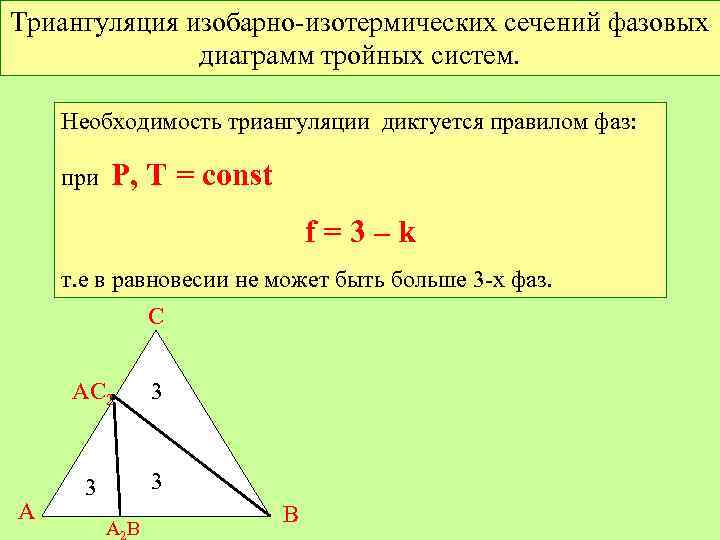
Триангуляция изобарно-изотермических сечений фазовых диаграмм тройных систем. Необходимость триангуляции диктуется правилом фаз: при Р, Т = const f=3–k т. е в равновесии не может быть больше 3 -х фаз. С АС 2 • А 3 3 3 АВ В
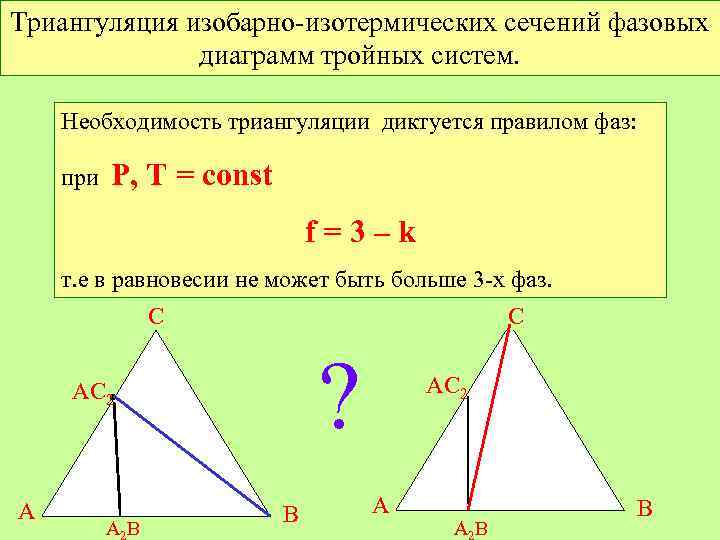
Триангуляция изобарно-изотермических сечений фазовых диаграмм тройных систем. Необходимость триангуляции диктуется правилом фаз: при Р, Т = const f=3–k т. е в равновесии не может быть больше 3 -х фаз. С С ? АС 2 • А АВ В АС 2 А АВ В

Принцип исключения нестабильных сечений при триангуляции. С АС 2 А А 2 В АС 2 + В ΔGr В А 2 В + С <0
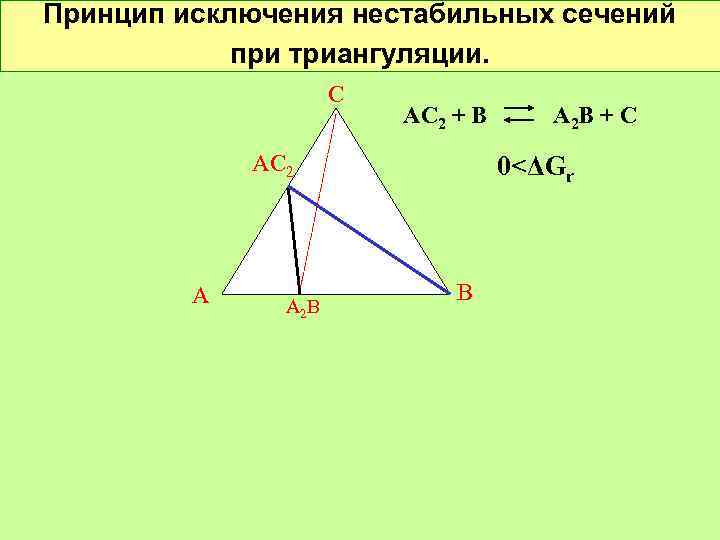
Принцип исключения нестабильных сечений при триангуляции. С АС 2 + В АС 2 А А 2 В А 2 В + С 0<ΔGr В
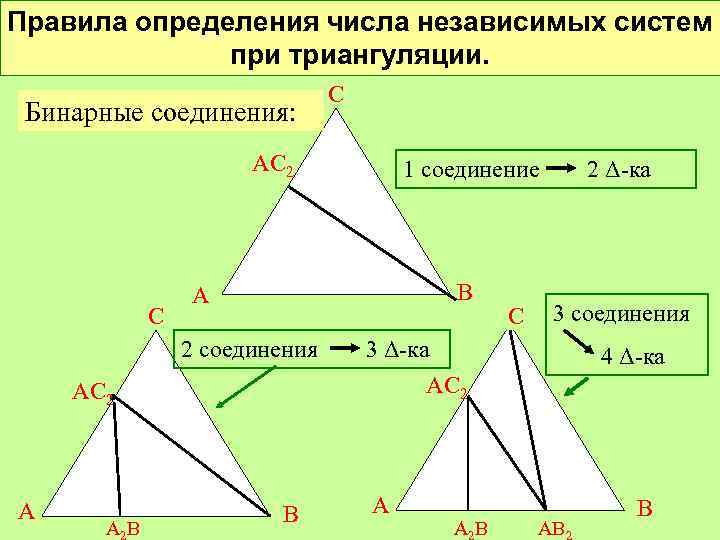
Правила определения числа независимых систем при триангуляции. Бинарные соединения: С АС 2 С В А 2 соединения АС 2 • А АВ 1 соединение В С 2 Δ-ка 3 соединения 3 Δ-ка АС 2 А АВ 4 Δ-ка АВ В
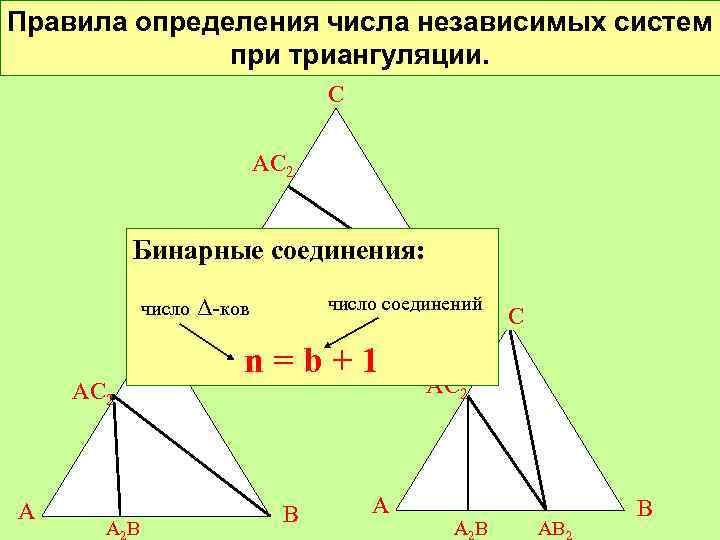
Правила определения числа независимых систем при триангуляции. С АС 2 Бинарные соединения: В А число Δ-ков С АС 2 • А АВ число соединений n=b+1 В А С АС 2 АВ АВ В
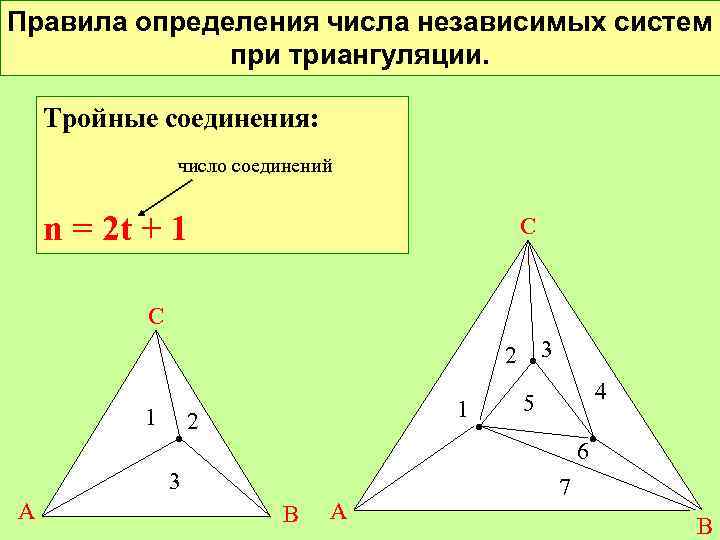
Правила определения числа независимых систем при триангуляции. Тройные соединения: АС 2 число соединений n = 2 t + 1 С С 2 • 3 1 • 1 2 3 А В А • 4 5 6 • 7 В
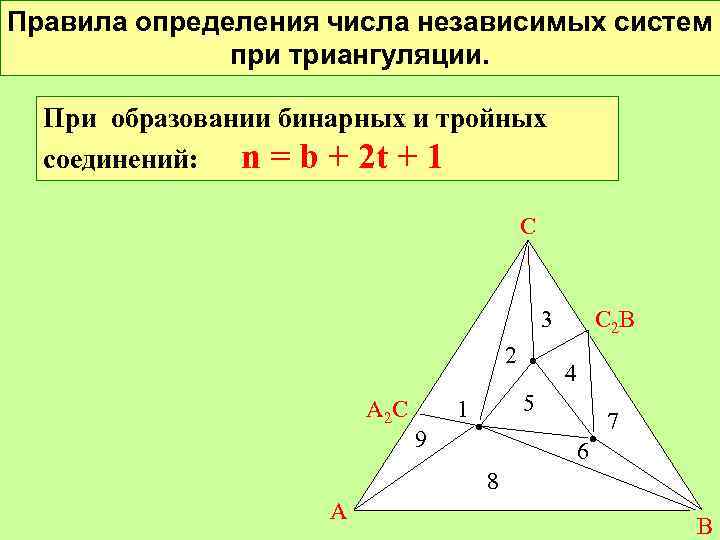
Правила определения числа независимых систем при триангуляции. При образовании бинарных и тройных соединений: n =2 b + 2 t + 1 АС С C 2 B 3 2 • A 2 C 1 9 4 5 • 6 • 7 8 А В
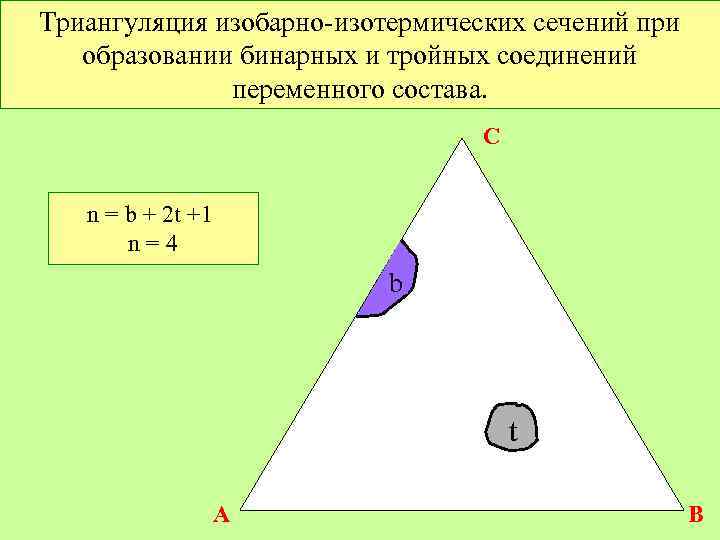
Триангуляция изобарно-изотермических сечений при образовании бинарных и тройных соединений переменного состава. C n = b + 2 t +1 n=4 b t A B
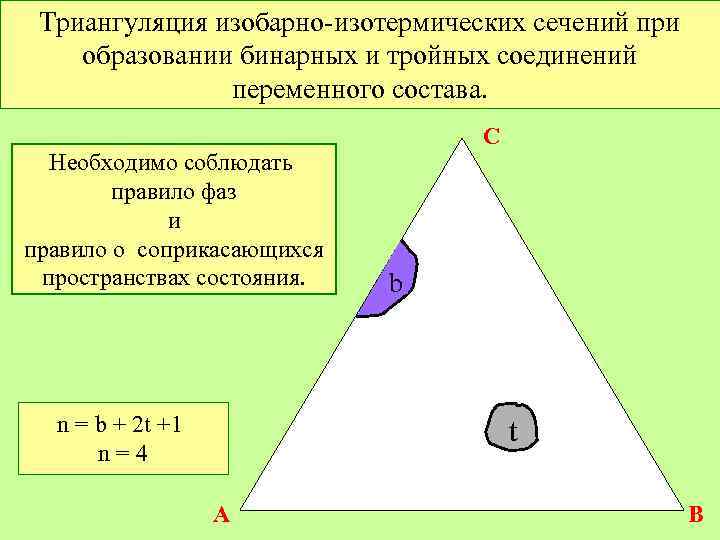
Триангуляция изобарно-изотермических сечений при образовании бинарных и тройных соединений переменного состава. Необходимо соблюдать правило фаз n = b + 2 t +1 и =4 правило о nсоприкасающихся пространствах состояния. n = b + 2 t +1 n=4 C b t A B
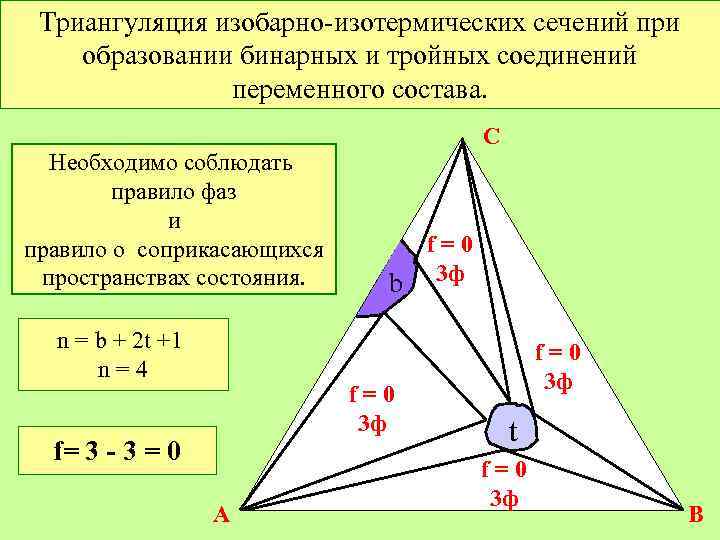
Триангуляция изобарно-изотермических сечений при образовании бинарных и тройных соединений переменного состава. Необходимо соблюдать правило фаз и правило о соприкасающихся пространствах состояния. n = b + 2 t +1 n=4 C b f=0 3 ф f= 3 - 3 = 0 A f=0 3 ф t f=0 3 ф B
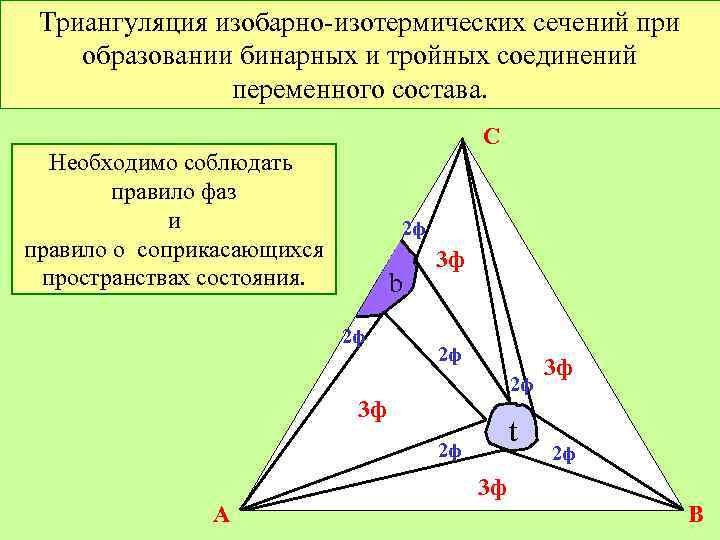
Триангуляция изобарно-изотермических сечений при образовании бинарных и тройных соединений переменного состава. C Необходимо соблюдать правило фаз и правило о соприкасающихся пространствах состояния. 2 ф b 2 ф 3 ф 2 ф 2 ф 3 ф t 2 ф 3 ф A B
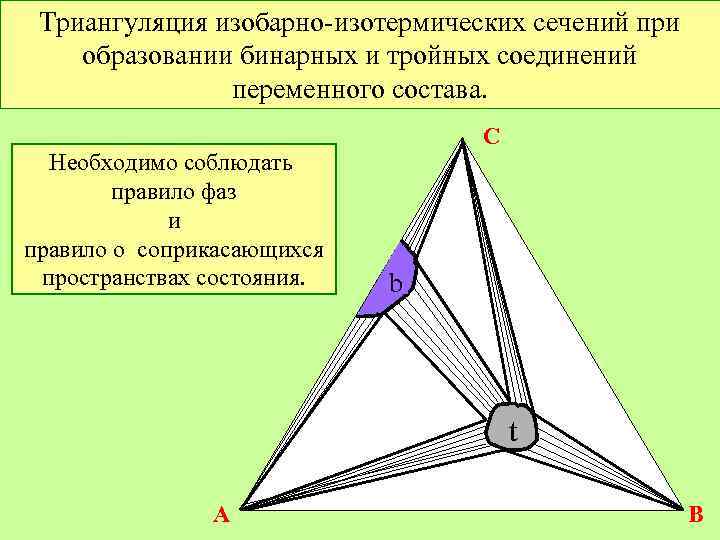
Триангуляция изобарно-изотермических сечений при образовании бинарных и тройных соединений переменного состава. Необходимо соблюдать правило фаз и правило о соприкасающихся пространствах состояния. C b t A B
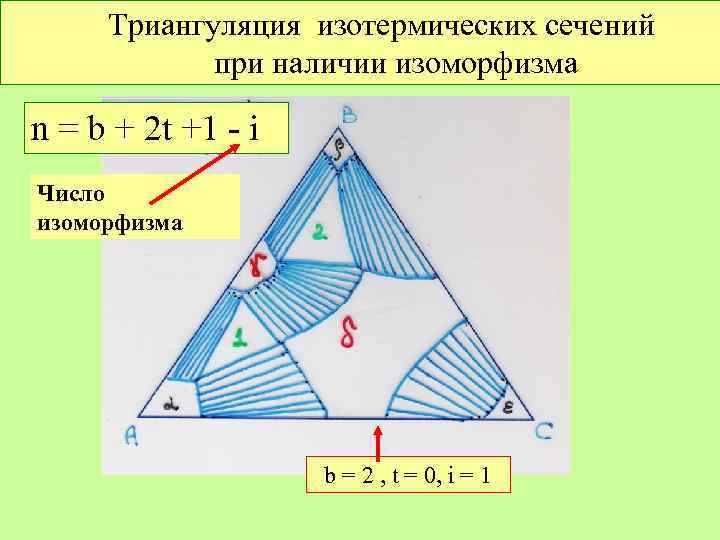
Триангуляция изотермических сечений при наличии изоморфизма n = b + 2 t +1 - i Число изоморфизма b = 2 , t = 0, i = 1
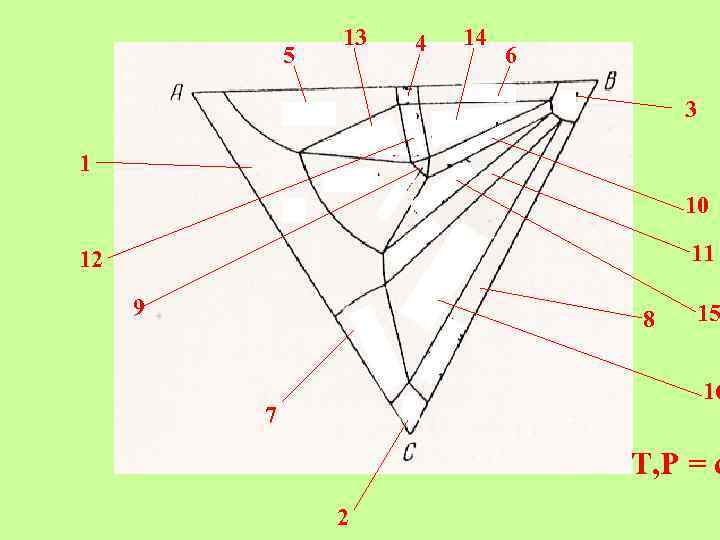
5 13 4 14 6 3 1 10 11 12 9 8 15 16 7 T, P = c 2
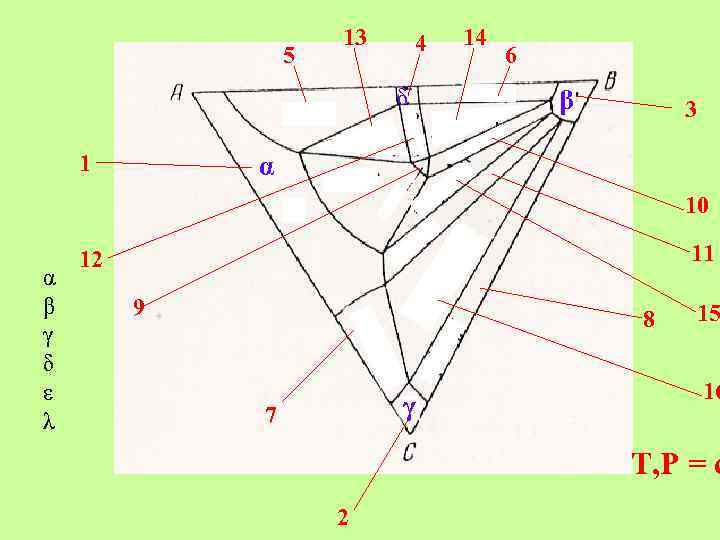
5 13 4 δ 1 14 6 β 3 α 10 α β γ δ ε λ 11 12 9 8 γ 7 15 16 T, P = c 2
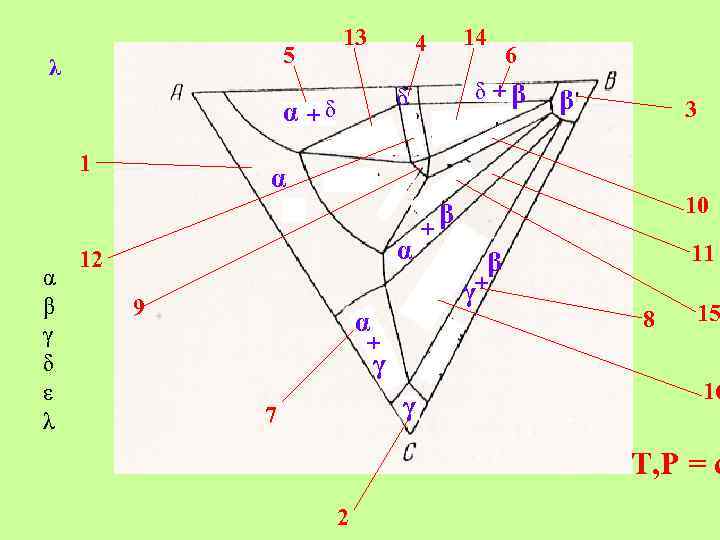
5 λ 13 α β γ δ ε λ 6 δ +β δ α +δ 1 14 4 β 3 α α 12 9 + γ γ 11 β γ+ α 7 + 10 β 8 15 16 T, P = c 2
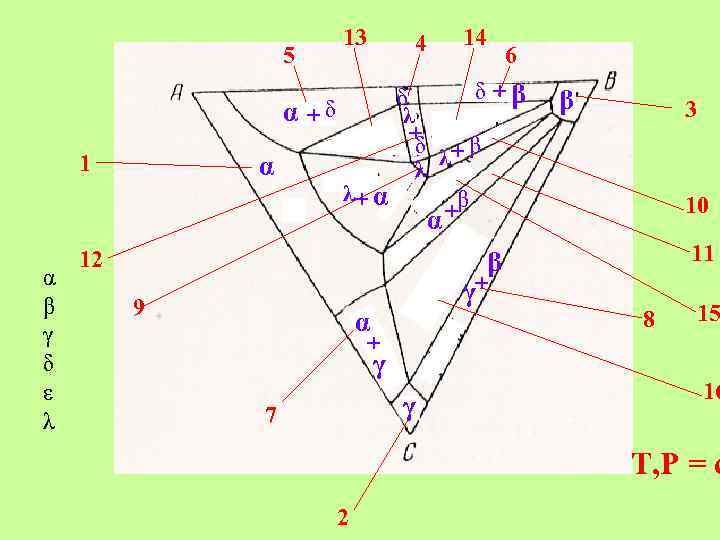
5 α +δ 1 α 13 14 4 6 δ +β δ λ + δ λ+ β λ λ+ α +β β 3 10 α α β γ δ ε λ 12 11 β 9 γ+ α + γ γ 7 8 15 16 T, P = c 2
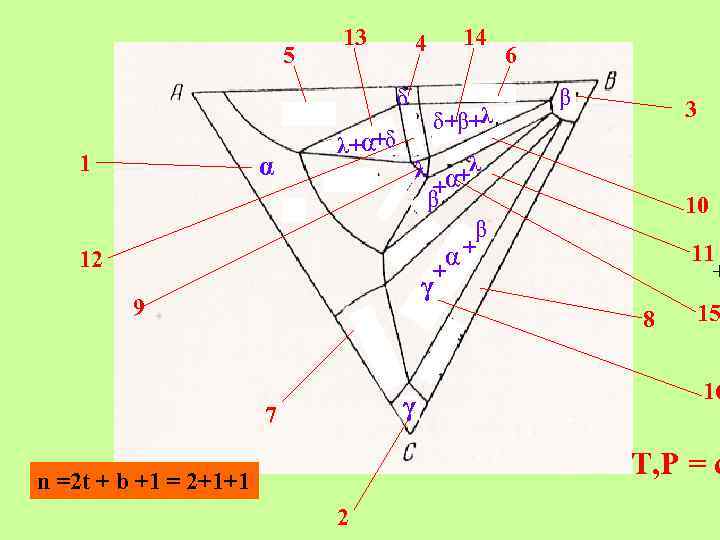
5 13 δ 1 α λ+α+δ 12 14 4 δ+β+λ 6 β 3 λ α+λ + β β α+ + 10 11 + γ 9 8 γ 7 15 16 T, P = c n =2 t + b +1 = 2+1+1 2

Lecture -Ternary systems.ppt