IV семестр Функция и эволюция n БЛОК 1

IV семестр «Функция и эволюция» n БЛОК 1 «Эволюция» – 4 занятия • • • Молекулярная филогенетика. Задачи и подходы. Лекциясеминар, 13. 02. (АБР) Реконструкция филогенетических деревьев. 2 практических занятия, 20. 02 и 27. 02 (САС, АБР) «Алгоритмы реконструкции филогенетических деревьев» . Лекция, семинар, обсуждение полученных результатов, 6. 03 (САС). Срок сдачи основного отчета – 5. 03 n n БЛОК 2 «Функции генов и их продуктов» – 4 занятия БЛОК 3 «Эволюция белкового семейства» – 5 занятий

Biologists must constantly keep in mind that what they see was not designed, but rather evolved. It might be thought, therefore, that evolutionary arguments would play a large part in guiding biological research, but this is far from the case. Francis Crick What Mad Pursuit (1988) pp. 138 -139

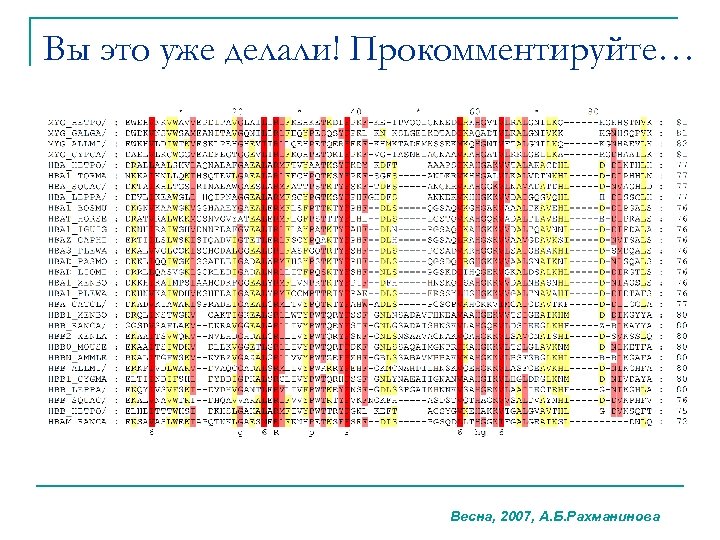
Вы это уже делали! Прокомментируйте… Весна, 2007, А. Б. Рахманинова

Молекулярная эволюция (молекулярная филогенетика) Весна, 2007, А. Б. Рахманинова

Молекулярная филогенетика ─ изучение филогенеза и эволюции путем анализа нуклеотидных и аминокислотных последовательностей

Основные этапы биоинформатического анализа молекулярной эволюции n n n Выбор последовательностей и их выравнивание Построение/выбор эволюционной модели Реконструкция эволюции q реконструкция филогенетического дерева q оценка силы давления и направления отбора q сравнение скоростей эволюции q. . . Оценка статистической значимости реконструкции ? Весна, 2007, А. Б. Рахманинова

Что будет? Выбор последовательностей и их выравнивание n Построение/выбор эволюционной модели § Реконструкция эволюции § реконструкция филогенетического дерева § оценка силы давления и направления отбора q сравнение скоростей эволюции q. . . § Оценка статистической значимости реконструкции n ! Весна, 2007, А. Б. Рахманинова

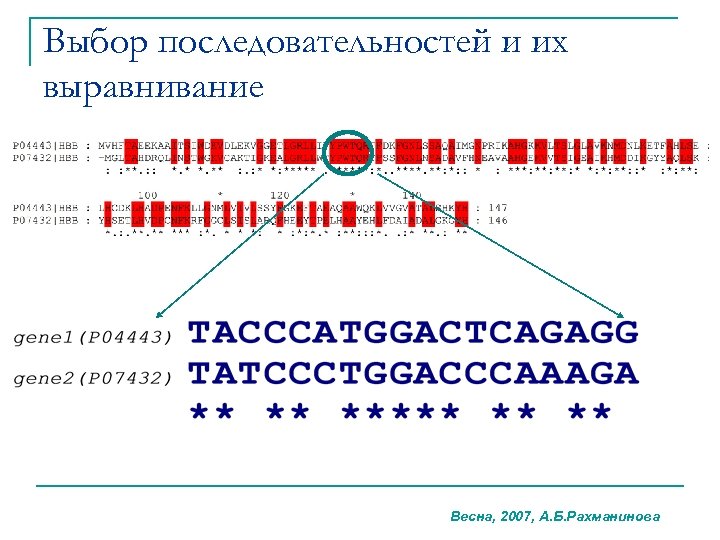
Выбор последовательностей и их выравнивание Весна, 2007, А. Б. Рахманинова

Выравнивание ? Весна, 2007, А. Б. Рахманинова

Выбор последовательностей и их выравнивание Весна, 2007, А. Б. Рахманинова

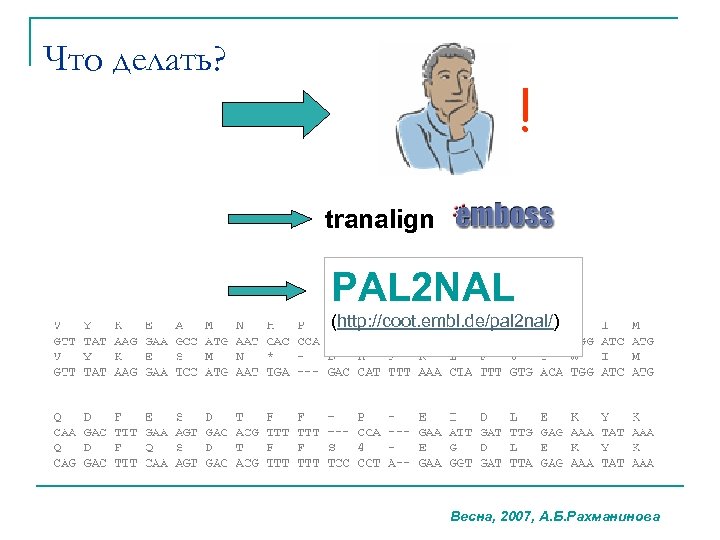
Что делать? ! tranalign PAL 2 NAL (http: //coot. embl. de/pal 2 nal/) Весна, 2007, А. Б. Рахманинова

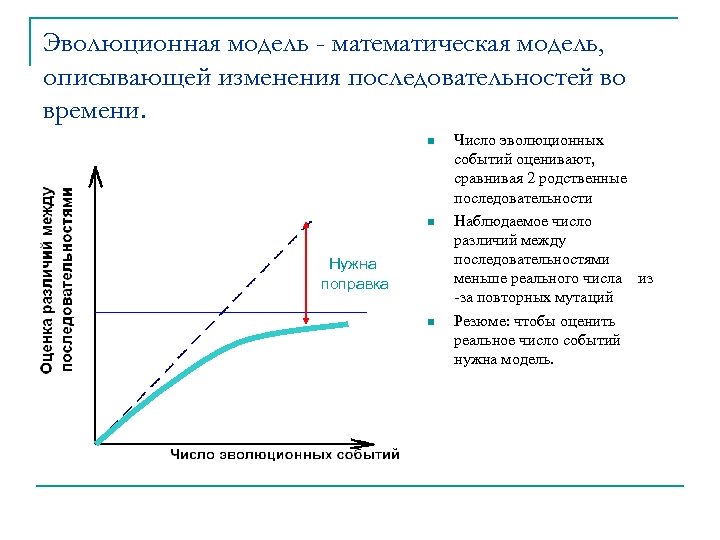
Эволюционная модель - математическая модель, описывающей изменения последовательностей во времени. n n Нужна поправка n Число эволюционных событий оценивают, сравнивая 2 родственные последовательности Наблюдаемое число различий между последовательностями меньше реального числа из -за повторных мутаций Резюме: чтобы оценить реальное число событий нужна модель.

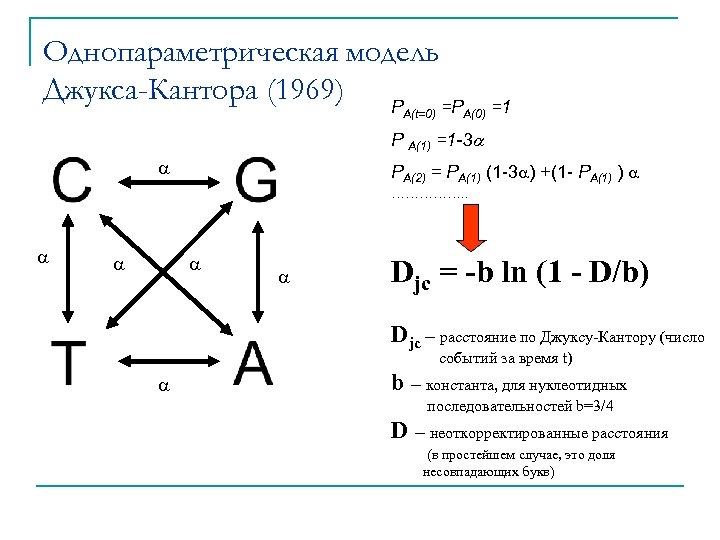
Однопараметрическая модель Джукса-Кантора (1969) P =P A(t=0) A(0) =1 P A(1) =1 -3 PA(2) = PA(1) (1 -3 ) +(1 - PA(1) ) ……………. . Djc = -b ln (1 - D/b) Djc – расстояние по Джуксу-Кантору (число событий за время t) b – константа, для нуклеотидных последовательностей b=3/4 D – неоткорректированные расстояния (в простейшем случае, это доля несовпадающих букв)

Однопараметрическая модель Джукса-Кантора Вероятность А в момент t PA(t=0) =PA(0)=1 PA(1) =1 -3 PA(2) = PA(1) (1 -3 ) +(1 - PA(1) ) PA(t+1) = PA(t) (1 -3 ) + (1 - PA(t)) d. PA(t) —— = - 4 PA(t) + dt PA(t) = 1/4 + (PA(0) -1/4) e -4 t PA(t) = 1/4 + 3/4 e-4 t для PA(0)=1 PA(t) = 1/4 - 1/4 e-4 t для PA(0)=0 Расстояние до предковой последовательности 1. Модель предполагает, что в 1 позиции в единицу времени происходит 3 замен. 2. Прошло время t, Djc – общее число замен/позицию за время t. 3. Доля совпадений/позицию между предковой и настоящей последовательностью? 4. Доля несовпадений/позицию между предковой и настоящей последовательностью? 5. Расстояние между предковой и настоящей последовательностью в смысле ожидаемого числа замен за время t (Djc ) - ?

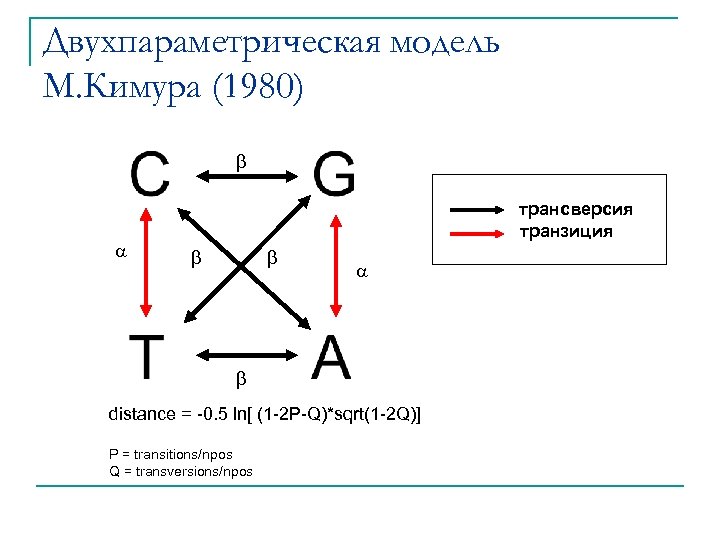
Двухпараметрическая модель М. Кимура (1980) трансверсия транзиция distance = -0. 5 ln[ (1 -2 P-Q)*sqrt(1 -2 Q)] P = transitions/npos Q = transversions/npos

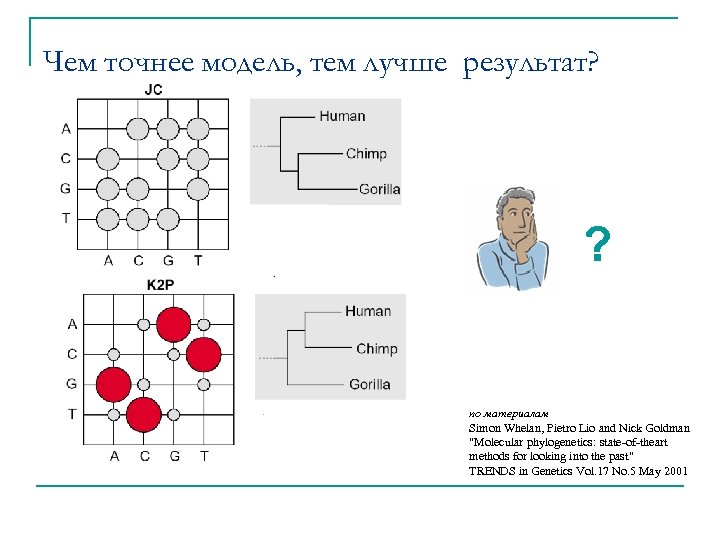
Чем точнее модель, тем лучше результат? ? по материалам Simon Whelan, Pietro Lio and Nick Goldman "Molecular phylogenetics: state-of-theart methods for looking into the past" TRENDS in Genetics Vol. 17 No. 5 May 2001

Сравнение скоростей эволюции разных генов 1. Thr-Ser-Ala… 2. Pro-Arg-Asp… 1. ACT AGT GCC… 2. ACA AGC GCT… ? 1. ACT AGT GCC… 2. CCT AGA GAC… Весна, 2007, А. Б. Рахманинова

KA/KS – мера давления естественного отбора Сравниваем 2 наблюдения: ATG GGG GCT GGG ATA GGA GAT GGA Несинонимичные замены 1 1 Синонимичные замены 1 1 KA/KS =1 PA Ps ? Ожидаемые значения: 5/6 4/6 1/6 2/6 KA/KS =5 KA/KS = 2 Нормируем на мутабильность последовательностей: KA/KS = 1/5 KA/KS = 1/2

KA/KS – мера давления естественного отбора n KA – число несинонимичных замен на 1 несинонимичный сайт n Ks – число синонимичных замен на 1 синонимичный сайт n Пример: Ka= 1 / 8. 67= 0. 12 Ks= 2/ 3. 33= 0. 6 Ka/Ks=0. 12 / 0. 6 =0. 19 (стабилизирующий отбор? )

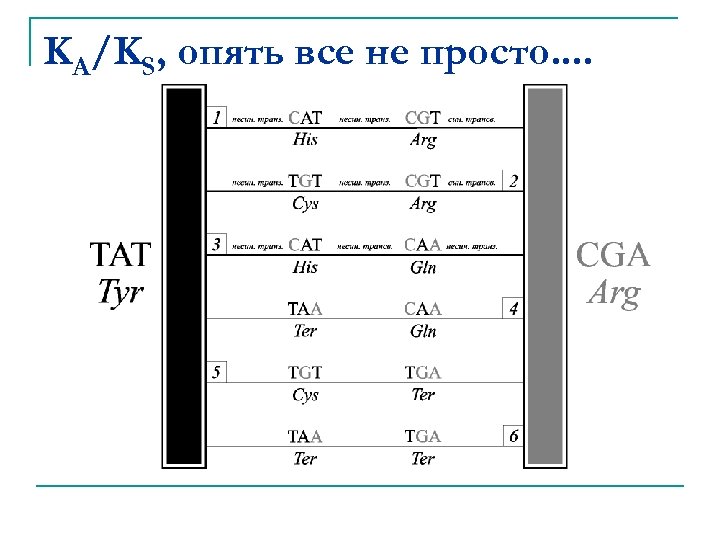
KA/KS, опять все не просто. .

KA/KS – мера давления естественного отбора KA – число несинонимичных замен на 1 несинонимичный сайт Ks – число синонимичных замен на 1 синонимичный сайт n n n KA / Ks << 1 KA / Ks > 1 отрицательный (стабилизирующий) отбор нейтральная эволюция положительный (движущий) отбор

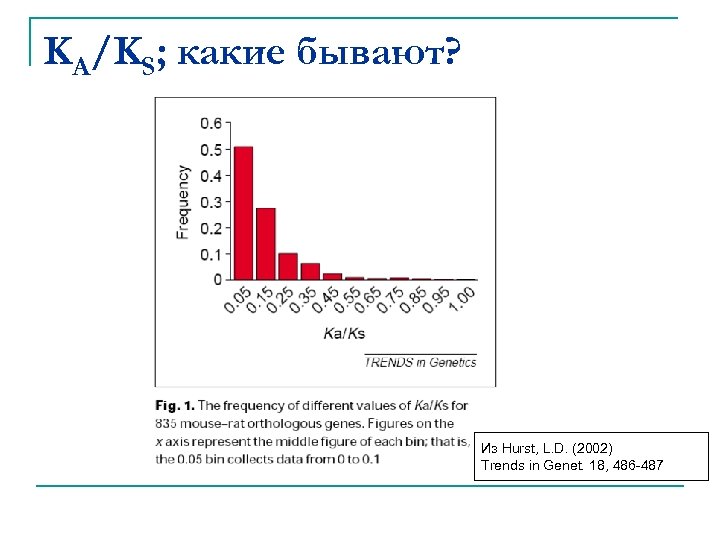
KA/KS; какие бывают? Из Hurst, L. D. (2002) Trends in Genet. 18, 486 -487

КАТЕГОРИИ ГЕНОВ ЧЕЛОВЕКА, ОБНАРУЖИВАЮЩИХ ПРИЗНАКИ ПОЛОЖИТЕЛЬНОГО ОТБОРА ВЗАИМОДЕЙСТВИЕ ПАТОГЕН-ХОЗЯИН ВОСПРОИЗВОДСТВО ПРИСПОСОБЛЕНИЕ К ПИТАНИЮ ВНЕШНОСТЬ СЕНСОРНЫЕ СИСТЕМЫ ПОВЕДЕНИЕ ОРГАНИЗАЦИЯ МОЗГА НЕИЗВЕСТНОГО НАЗНАЧЕНИЯ E. J. Vallender, B. T. Lahn. Hum. Mol. Gen. 2004, V. 13, Rev. Issue 2, R 245 -R 254

Ждите лекций А. В. Алешина по теории эволюции и лекций М. С. Гельфанда по сравнительной геномике!!