IV Частотные характеристики цепей 4 1 Комплексные

IV Частотные характеристики цепей

4. 1 Комплексные передаточные функции

Комплексные передаточные функции (КПФ) – отношение комплексной амплитуды реакции цепи к комплексной амплитуде воздействия

Виды КПФ: безразмерные а) по напряжению b) по току или

c) Комплексное передаточное сопротивление (Ом) или d) Комплексная передаточная проводимость (См) или

Комплексные входные функции Комплексное входное сопротивление Комплексная входная проводимость 2 П

Формы представления КПФ а) алгебраическая б) показательная

Годограф передаточной функции - это некоторая кривая, вычерчиваемая вектором комплексной плоскости при изменении частоты от 0 до на

Логарифмическая АЧХ Используется в том случае, когда изменяется в очень широких пределах при изменении частоты

Ослабление цепи

Пример:

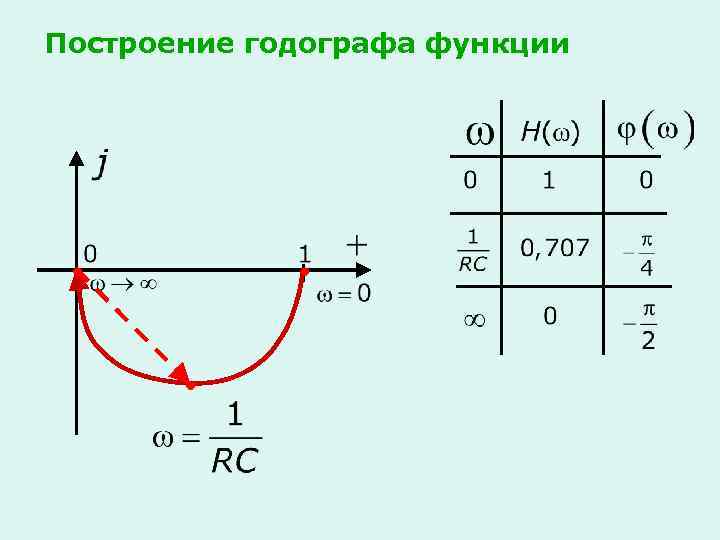Построение годографа функции

Качественное построение АЧХ Построение ведется по характерным точкам Число характерных точек = число реактивных элементов+1

По формуле:

По схеме: Для того, чтобы построить АЧХ цепи, необходимо нарисовать ее схемы для характерных точек и найти значение КПФ в каждой схеме

4. 2 Резонанс напряжений. Последовательный колебательный контур

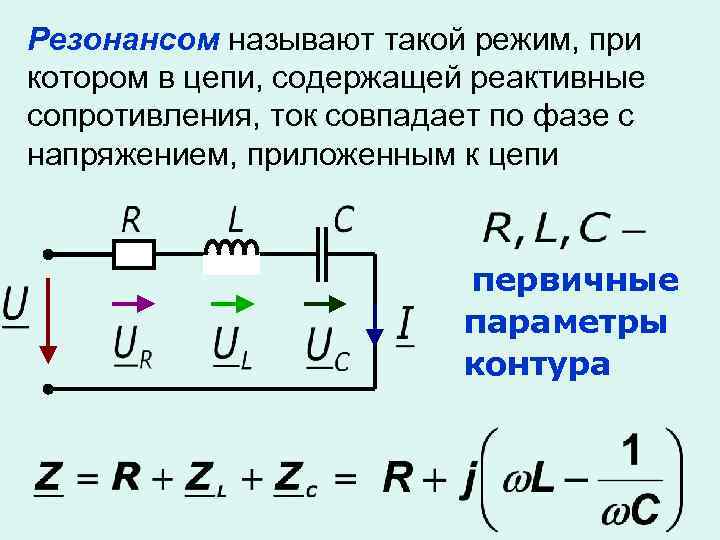Резонансом называют такой режим, при котором в цепи, содержащей реактивные сопротивления, ток совпадает по фазе с напряжением, приложенным к цепи первичные параметры контура

I

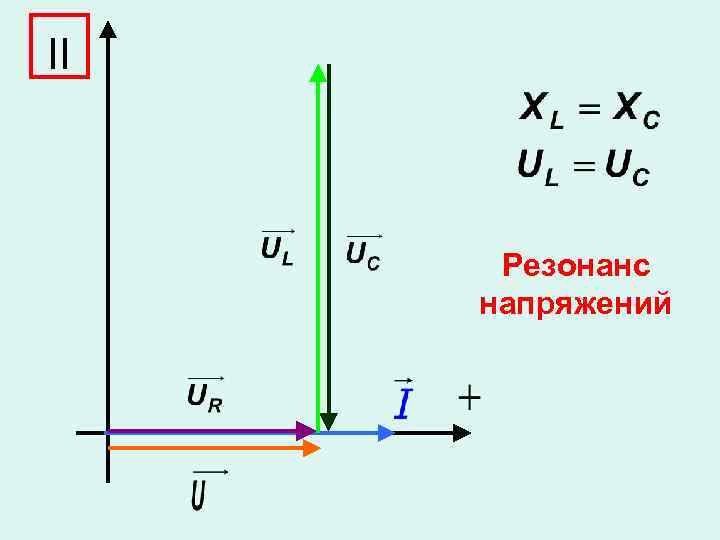II Резонанс напряжений

III

Условие резонанса

Вторичные параметры контура 1. Частота резонанса 2. Характеристическое сопротивление контура

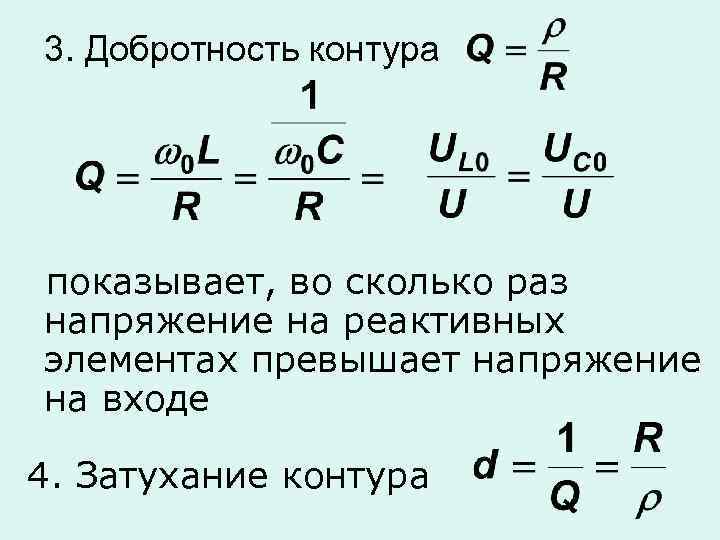3. Добротность контура показывает, во сколько раз напряжение на реактивных элементах превышает напряжение на входе 4. Затухание контура

Признаки резонанса напряжений 1. Напряжение, приложенное к контуру, и ток в контуре совпадают по фазе 2. Входное сопротивление контура минимально и равно

3. Ток в контуре достигает максимальной величины 4. Действующие значения напряжений на индуктивности и емкости равны и в раз превышают входное напряжение

4. 3 Энергетические соотношения при резонансе напряжений.

Мгновенная энергия электромагнитного контура

• При резонансе происходит обмен энергией между индуктивностью и емкостью • Когда индуктивность возвращает энергию в цепь, емкость ее забирает и наоборот • Реактивная мощность источника, поступающая в цепь при резонансе, равна нулю

• Колебаний энергии от генератора к приемнику нет • Энергия, запасенная в контуре при подключении его к источнику, «колеблется» при резонансе между индуктивностью и емкостью без участия источника. Поэтому контур называют колебательным.

• У генератора контур забирает столько энергии, сколько рассеивается на активном сопротивлении R • Если активное сопротивление контура R равно нулю (идеальный контур), то потери в контуре отсутствуют и при отключении источника колебания будут продолжаться бесконечно долго

Способность контура сохранять энергию оценивается добротностью

4. 4 Частотные характеристики последовательного колебательного контура

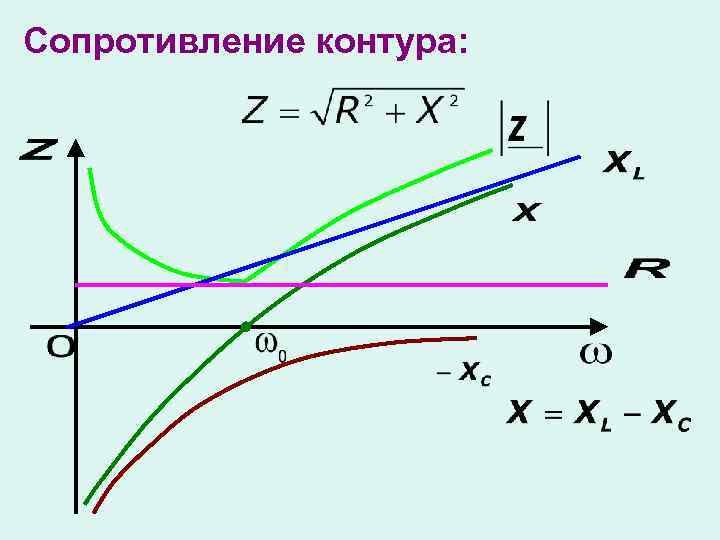Сопротивление контура:

Ток в контуре

Частотные характеристики напряжений

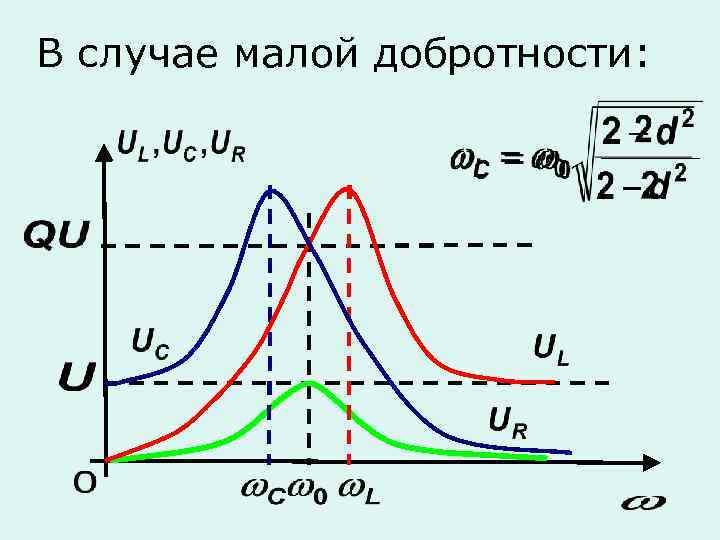В случае малой добротности:

Влияние добротности на частотные характеристики контура

тогда:

Степень отклонения режима колебательного контура от резонанса оценивают расстройками 1. абсолютная расстройка 2. относительная расстройка

3. Обобщенная расстройка Если контур настроен на резонанс, то все расстройки равны нулю

Область малых расстроек – нормальный режим работы контура

Точная формула Приближенная формула

Нормированные частотные характеристики ≈1 Для области малых расстроек ≈1

Полоса пропускания (ПП) - диапазон частот, на границах которого средняя мощность, поглощаемая контуром, равна половине мощности, поглощаемой контуром при резонансной частоте на границах ПП ток или напряжение уменьшаются в раз по сравнению с их максимальным значением

Полоса пропускания

• Абсолютная полоса пропускания • Относительная полоса пропускания

Нормированная частотная характеристика тока на границах полосы пропускания:

Чем больше добротность, тем уже полоса пропускания и лучше избирательность контура Избирательность – способность пропускать полезные сигналы и не пропускать вредные (помехи)

4. 5 Передаточные функции последовательного колебательного контура

Последовательный контур как усилитель напряжения

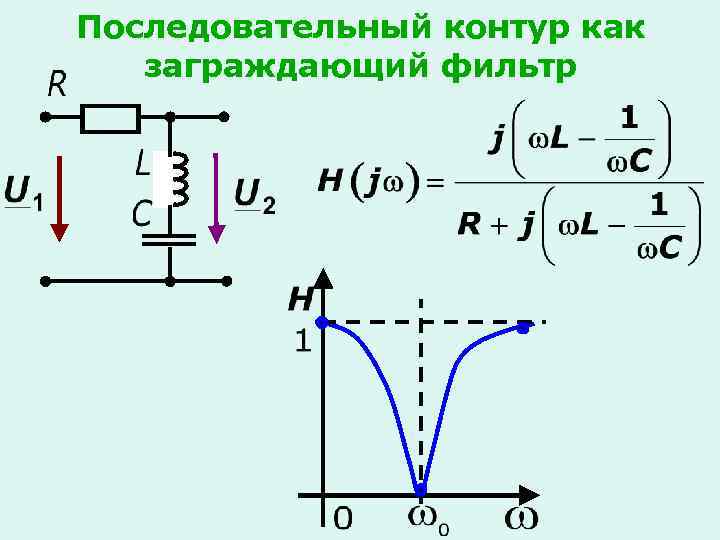Последовательный контур как заграждающий фильтр

4. 6 Влияние источника сигнала и нагрузки на последовательный контур

Влияние источника

• Источник сигнала уменьшает добротность контура • Последовательный контур работает только с источниками напряжения

Влияние нагрузки

Активное сопротивление нагрузки может изменять резонансную частоту контура

Резонансная частота не изменяется

4. 7 Резонанс токов. Параллельный колебательный контур.

Резонанс токов возникает в цепи, содержащей параллельные ветви, имеющие индуктивный и емкостной характер.

эквивалентная проводимость контура:

Условие резонанса токов

Резонанс токов возникает, если: а) б) в) – случай «безразличного» резонанса, на любой частоте проводимость контура носит активный характер

- сопротивление контура на резонансной частоте

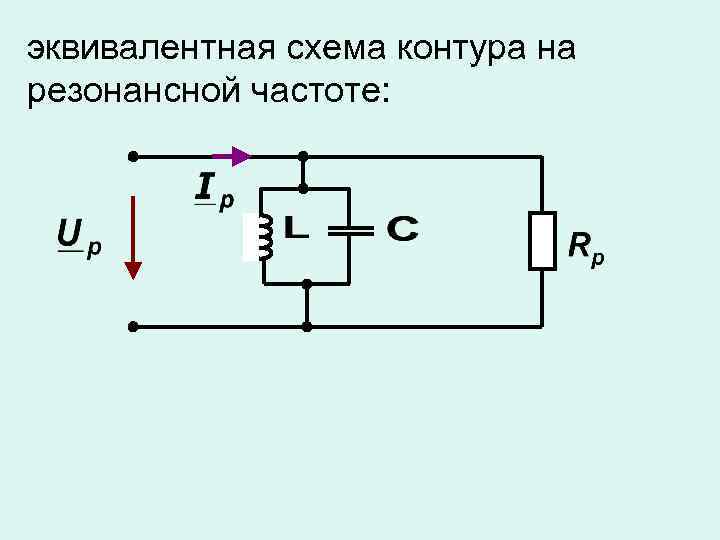эквивалентная схема контура на резонансной частоте:

4. 8 Частные случаи резонансов

1) Идеальный контур (без потерь)

Частотные характеристики Комплексная проводимость контура Реактивная проводимость ветвей Реактивная проводимость контура

Комплексные токи в ветвях: Входной ток:

2) Высокодобротный контур

Вывод: Токи в индуктивной и емкостной ветвях при резонансе в Q раз больше общего тока контура. Поэтому резонанс в параллельном контуре называют резонансом токов.

Векторная диаграмма

Область малых расстроек

4. 9 Влияние источника сигнала и нагрузки на параллельный контур

1) Влияние источника

Относительное напряжение на контуре:

обобщенная расстройка с учетом внутреннего сопротивления генератора:

Выводы: для получения высокой избирательности параллельный контур всегда должен работать с генератором, имеющим максимально возможное внутреннее сопротивление, т. е. с генератором тока. Параллельный контур не усиливает сигнал, а только его избирает

2) Влияние нагрузки