652ffe567a13a7b1b22a37866fadac27.ppt
- Количество слайдов: 19

ITERATIVE DICHOTOMISER (ID 3) ALGORITHM By: Phuong H. Nguyen Professor: Lee, Sin-Min Course: CS 157 B Section: 2 Date: 05/08/07 Spring 2007

Overview Introduction Entropy Information Gain Detailed Example Walkthrough Conclusion References

Introduction ID 3 algorithm is a greedy algorithm for decision tree construction developed by Ross Quinlan in 1987. ID 3 algorithm uses information gain to select best attribute: Max-Gain (highest gain) for splitting Attribute with most useful information to split

Entropy Measure the impurity or randomness of an example collection. A quantitative measurement of the homogeneity of a set of examples. In other words, it tells us how well an attribute separating the given examples according to the target classification class.

Entropy (cont. ) Entropy (S) = -Ppositive log 2 Ppositive – Pnegative log 2 Pnegative Where: - P = proportion of positive examples - P = proportion of negative examples positive negative Example: If S is a collection of 14 examples with 9 YES and 5 NO, then: Entropy(S) = - (9/14) log (9/14) - (5/14) log (5/14) = 0. 940 2 2

Entropy (cont. ) More than two values: Entropy(S) = ∑ -p(i) log 2 p(i) - Result will be between 0 and 1. Special cases: - If Entropy(S) = 0 all members in S belong to strictly one class (max uniformity, min randomness) Age Income Buys Computer <= 20 Low Yes 21… 40 High Yes >40 Medium Yes If Entropy(S) = 1(max value) members are split equally between the two classes (min uniformity, max randomness) Age Income Buys Computer <15 Low No >= 25 High Yes

Information Gain A statistical property measures how well a given attribute separates example collection into target classes. ID 3 algorithm uses highest information (most useful for classification) to select best attribute

Information Gain (cont. ) Gain(S, A) = Entropy(S) – ∑((|Sv| / |S|) *Entropy(Sv)) Where: A is an attribute of collection S Sv = subset of S for which attribute A has value v |Sv| = number of elements in Sv |S| = number of elements in S

Information Gain (cont. ) Example: Collection S = 14 examples (9 YES - 5 NO) Wind speed is one attribute of S = {Weak, Strong} - Weak = 8 occurrences (6 YES - 2 NO) Strong = 6 occurrences (3 YES - 3 NO) Calculation: Entropy(S) = - (9/14) log 2 (9/14) - (5/14) log 2 (5/14) = 0. 940 Entropy(Sweak) = - (6/8)*log 2(6/8) - (2/8)*log 2(2/8) = 0. 811 Entropy(Sstrong) = - (3/6)*log 2(3/6) = 1. 00 Gain(S, Wind) = Entropy(S) - (8/14)*Entropy(Sweak) - (6/14)*Entropy(Sstrong) = 0. 940 - (8/14)*0. 811 - (6/14)*1. 00 = 0. 048 - For each attribute in S, the gain is calculated and the highest gain is used in the root node or decision node.

Example Walkthrough Example of company sending out some promotion to various houses and recording a few facts about each house and also whether people responded or not: District House Type Income Previous Customer Outcome Suburban Detached High No Nothing Suburban Detached High Responded Nothing Rural Detached High No Responded Urban Semi-detached Low Responded Nothing Rural Semi-detached Low Responded Suburban Terrace High No Nothing Suburban Semi-detached Low No Responded Urban Terrace Low No Responded Suburban Terrace Low Responded Rural Terrace High Responded Rural Detached Low No Responded Urban Terrace High Responded Nothing
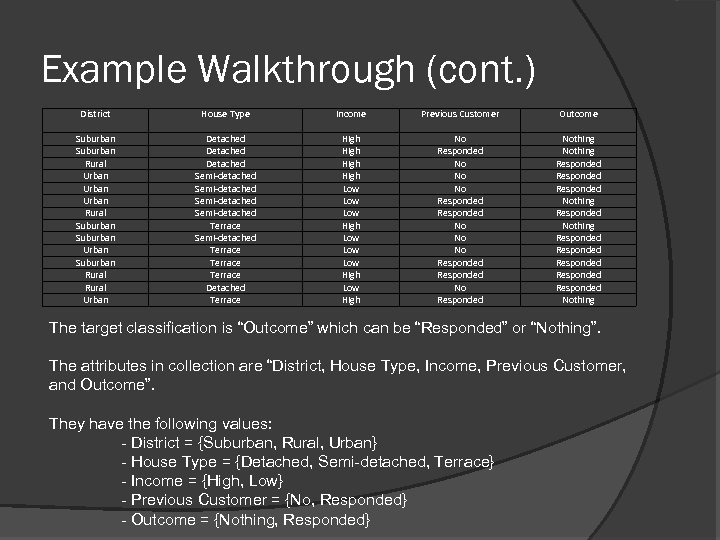
Example Walkthrough (cont. ) District House Type Income Previous Customer Outcome Suburban Rural Urban Rural Suburban Urban Suburban Rural Urban Detached Semi-detached Terrace Semi-detached Terrace Detached Terrace High Low Low Low High No Responded No No No Responded Nothing Responded Nothing Responded Responded Nothing The target classification is “Outcome” which can be “Responded” or “Nothing”. The attributes in collection are “District, House Type, Income, Previous Customer, and Outcome”. They have the following values: - District = {Suburban, Rural, Urban} - House Type = {Detached, Semi-detached, Terrace} - Income = {High, Low} - Previous Customer = {No, Responded} - Outcome = {Nothing, Responded}
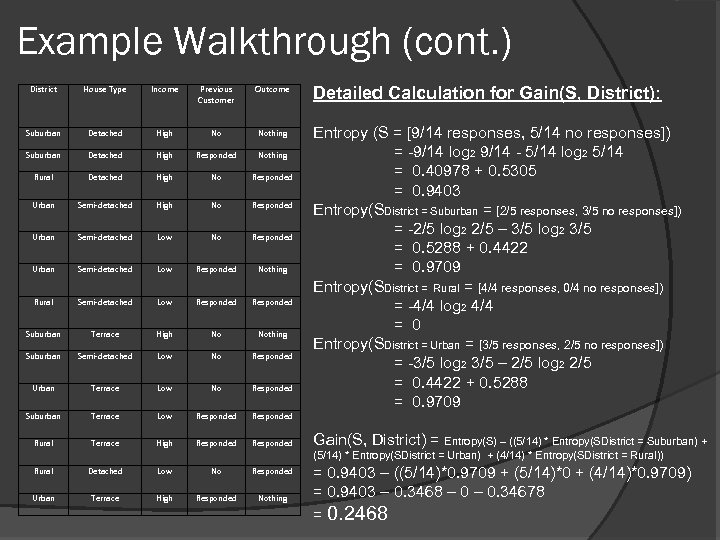
Example Walkthrough (cont. ) District House Type Income Previous Customer Outcome Detailed Calculation for Gain(S, District): Suburban Detached High No Nothing Suburban Detached High Responded Nothing Rural Detached High No Responded Urban Semi-detached Low Responded Nothing Rural Semi-detached Low Responded Suburban Terrace High No Nothing Suburban Semi-detached Low No Responded Urban Terrace Low No Responded Entropy (S = [9/14 responses, 5/14 no responses]) = -9/14 log 2 9/14 - 5/14 log 2 5/14 = 0. 40978 + 0. 5305 = 0. 9403 Entropy(SDistrict = Suburban = [2/5 responses, 3/5 no responses]) = -2/5 log 2 2/5 – 3/5 log 2 3/5 = 0. 5288 + 0. 4422 = 0. 9709 Entropy(SDistrict = Rural = [4/4 responses, 0/4 no responses]) = -4/4 log 2 4/4 = 0 Entropy(SDistrict = Urban = [3/5 responses, 2/5 no responses]) = -3/5 log 2 3/5 – 2/5 log 2 2/5 = 0. 4422 + 0. 5288 = 0. 9709 Suburban Terrace Low Responded Rural Terrace High Responded Gain(S, District) = Entropy(S) – ((5/14) * Entropy(SDistrict = Suburban) + (5/14) * Entropy(SDistrict = Urban) + (4/14) * Entropy(SDistrict = Rural)) Rural Detached Low No Responded Urban Terrace High Responded Nothing = 0. 9403 – ((5/14)*0. 9709 + (5/14)*0 + (4/14)*0. 9709) = 0. 9403 – 0. 3468 – 0. 34678 = 0. 2468

Example Walkthrough (cont. ) So we now have: Gain(S, District) = 0. 2468 Apply the same process to the remaining 3 attributes of S, we get: - Gain(S, House Type) = 0. 049 - Gain(S, Income) = 0. 151 - Gain(S, Previous Customer) = 0. 048 Comparing the information gain of the four attributes, we see that “District” has the highest value. District will be the root node of the decision tree. So far the decision tree will look like following: District Suburban ? ? ? Rural Urban ? ? ?

Example Walkthrough (cont. ) Apply the same process to the left side of the root node (Suburban), we get: - Entropy(Ssuburban) = 0. 970 - Gain(Ssuburban, House Type) = 0. 570 - Gain(Ssuburban, Income) = 0. 970 - Gain(Ssuburban, Previous Customer) = 0. 019 The information gain of “Income” is highest: Income will be the decision node. The decision tree will look like following: District Suburban Income Rural Urban ? ? ?

Example Walkthrough (cont. ) For the center of the root node (Rural), it is a special case because: - Entropy(SRural) = 0 all members in SRural belong to strictly one target classification class (responded) Thus, we skip all the calculation and add the corresponding target classification value to the tree. The decision will look like following: District Suburban Income Rural Responded Urban ? ? ?

Example Walkthrough (cont. ) Apply the same process to the right side of the root node (Urban), we get: - Entropy(Surban) = 0. 970 - Gain(Surban, House Type) = 0. 019 - Gain(Surban, Income) = 0. 019 - Gain(Surban, Previous Customer) = 0. 970 The information gain of “Previous Customer” is highest: Previous Customer will be the decision node. The decision tree will look like following: District Suburban Income Rural Responded Urban Previous Customer
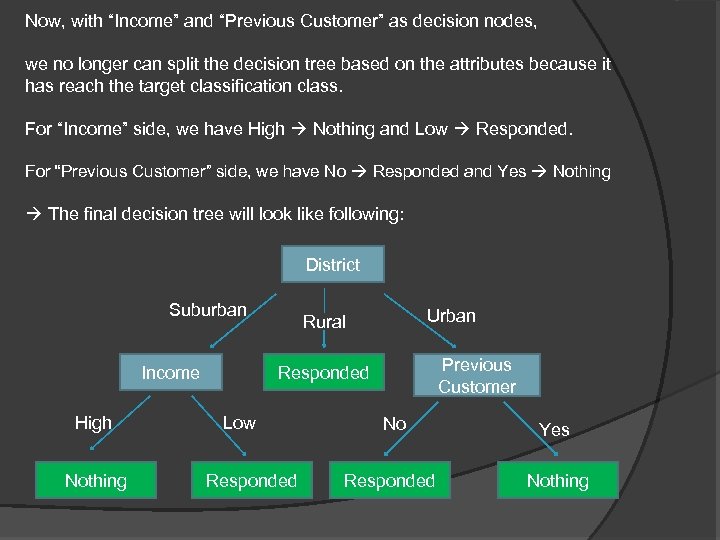
Now, with “Income” and “Previous Customer” as decision nodes, we no longer can split the decision tree based on the attributes because it has reach the target classification class. For “Income” side, we have High Nothing and Low Responded. For “Previous Customer” side, we have No Responded and Yes Nothing The final decision tree will look like following: District Suburban Income High Nothing Urban Rural Previous Customer Responded Low Responded No Yes Responded Nothing

Conclusion ID 3 algorithm is easy to use if we know how it works. Industry has shown that ID 3 has been effective for data mining. ID 3 algorithm is one of the most important techniques in data mining.

References Dr. Lee’s Slides, San Jose State University, Spring 2007 "Building Decision Trees with the ID 3 Algorithm", by: Andrew Colin, Dr. Dobbs Journal, June 1996 "Incremental Induction of Decision Trees", by Paul E. Utgoff, Kluwer Academic Publishers, 1989 http: //www. cise. ufl. edu/~ddd/cap 6635/Fall 97/Short-papers/2. htm http: //decisiontrees. net/node/27
652ffe567a13a7b1b22a37866fadac27.ppt