c920f0dee48f3b4548024dc08c5e21b4.ppt
- Количество слайдов: 28

Item Pricing for Revenue Maximization in Combinatorial Auctions Maria-Florina Balcan, Carnegie Mellon University Joint with Avrim Blum and Yishay Mansour

Outline of the Talk Revenue Maximization in Combinatorial Auctions • Item Pricing in Unlimited Supply Combinatorial Auctions • Single-minded bidders. [Balcan-Blum’ 06] • General bidders. [Balcan-Blum-Mansour’ 07] • Item Pricing in Limited Supply Combinatorial Auctions • Bidders with subadditive valuations. [Balcan-Blum-Mansour’ 07]

Supermarket Pricing Problem • A supermarket trying to decide on how to price the goods. Seller’s Goal: set prices to maximize revenue. • Simple case: customers make separate decisions on each item. • Harder case: customers buy everything or nothing based on sum of prices in list. • Or could be even more complex. “Unlimited supply combinatorial auction with additive / single -minded /unit-demand/ general bidders”

Supermarket Pricing Problem Various recent results have been focused on single minded and unit demand consumers. Algorithmic • Seller knows the market well. Incentive Compatible Auction • Must be in customers’ interest (dominant strategy) to report truthfully. Online Pricing • Customers arrive one at a time, buy what they want at current prices. Seller modifies prices over time.
![Algorithmic Problem, Single-minded Bidders [BB’ 06] • n item types (coffee, cups, sugar, apples), Algorithmic Problem, Single-minded Bidders [BB’ 06] • n item types (coffee, cups, sugar, apples),](https://present5.com/presentation/c920f0dee48f3b4548024dc08c5e21b4/image-5.jpg)
Algorithmic Problem, Single-minded Bidders [BB’ 06] • n item types (coffee, cups, sugar, apples), with unlimited supply of each. • m customers. • Customer i has a shopping list Li and will only shop if the total cost of items in Li is at most some amount wi • All marginal costs are 0, and we know all the (Li, wi). What prices on the items will make you the most money? • Easy if all Li are of size 1. • What happens if all Li are of size 2?
![Algorithmic Problem, Single-minded Bidders [BB’ 06] • A multigraph G with values we on Algorithmic Problem, Single-minded Bidders [BB’ 06] • A multigraph G with values we on](https://present5.com/presentation/c920f0dee48f3b4548024dc08c5e21b4/image-6.jpg)
Algorithmic Problem, Single-minded Bidders [BB’ 06] • A multigraph G with values we on edges e. • Goal: assign prices on vertices to maximize total profit, where: 5 15 10 30 40 10 20 5 Unlimited supply • APX hard [GHKKKM’ 05].
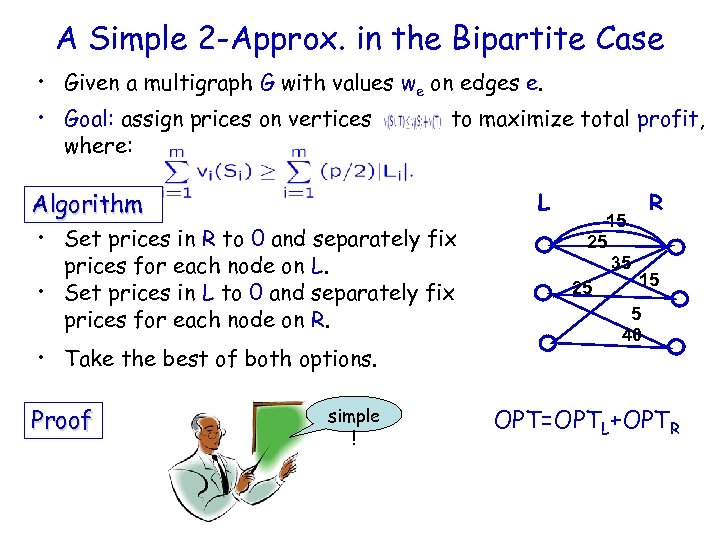
A Simple 2 -Approx. in the Bipartite Case • Given a multigraph G with values we on edges e. • Goal: assign prices on vertices where: to maximize total profit, Algorithm L • Set prices in R to 0 and separately fix prices for each node on L. • Set prices in L to 0 and separately fix prices for each node on R. • Take the best of both options. Proof simple ! R 15 25 35 15 25 5 40 OPT=OPTL+OPTR
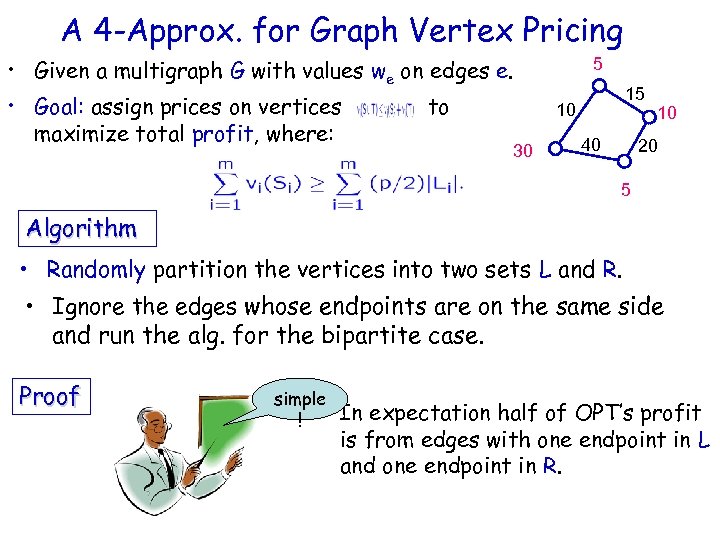
A 4 -Approx. for Graph Vertex Pricing • Given a multigraph G with values we on edges e. • Goal: assign prices on vertices maximize total profit, where: to 5 15 10 30 40 10 20 5 Algorithm • Randomly partition the vertices into two sets L and R. • Ignore the edges whose endpoints are on the same side and run the alg. for the bipartite case. Proof simple ! In expectation half of OPT’s profit is from edges with one endpoint in L and one endpoint in R.

Algorithmic Pricing, Single-minded Bidders, k-hypergraph Problem 15 What about lists of size · k? 10 Algorithm 20 – Put each node in L with probability 1/k, in R with probability 1 – 1/k. – Let GOOD = set of edges with exactly one endpoint in L. Set prices in R to 0 and optimize L wrt GOOD. • Let OPTj, e be revenue OPT makes selling item j to customer e. Let Xj, e be indicator RV for j 2 L & e 2 GOOD. • Our expected profit at least:
![Algorithmic Problem, Single-minded Bidders [BB’ 06] Summary: • 4 approx for graph case. • Algorithmic Problem, Single-minded Bidders [BB’ 06] Summary: • 4 approx for graph case. •](https://present5.com/presentation/c920f0dee48f3b4548024dc08c5e21b4/image-10.jpg)
Algorithmic Problem, Single-minded Bidders [BB’ 06] Summary: • 4 approx for graph case. • O(k) approx for k-hypergraph case. Improves the O(k 2) approximation [BK’ 06]. Can also apply the [B-B-Hartline-M’ 05] reductions to obtain good truthful mechanisms. Can be naturally adapted to the online setting.
![Algorithmic Problem, Single-minded Bidders [BB’ 06] Other known results: • O(log mn) approx. by Algorithmic Problem, Single-minded Bidders [BB’ 06] Other known results: • O(log mn) approx. by](https://present5.com/presentation/c920f0dee48f3b4548024dc08c5e21b4/image-11.jpg)
Algorithmic Problem, Single-minded Bidders [BB’ 06] Other known results: • O(log mn) approx. by picking the best single price [GHKKKM 05]. • (log n) hardness for general case [DFHS 06].
What about the most general case? 20$ 100$ 5$ 25$ 30$ 1$ 20$ 30$
![General Bidders Can we say anything at all? ? Can extend [GHKKKM 05] and General Bidders Can we say anything at all? ? Can extend [GHKKKM 05] and](https://present5.com/presentation/c920f0dee48f3b4548024dc08c5e21b4/image-13.jpg)
General Bidders Can we say anything at all? ? Can extend [GHKKKM 05] and get a log-factor approx for general bidders by an item pricing. Theorem There exists a price a p which gives a log(m) +log (n) approximation to the total social welfare.
![General Bidders • Can extend [GHKKKM 05] and get a log-factor approx for general General Bidders • Can extend [GHKKKM 05] and get a log-factor approx for general](https://present5.com/presentation/c920f0dee48f3b4548024dc08c5e21b4/image-14.jpg)
General Bidders • Can extend [GHKKKM 05] and get a log-factor approx for general bidders by an item pricing. Note: if bundle pricing is allowed, can do it easily. – Pick a random admission fee from {1, 2, 4, 8, …, h} to charge everyone. – Once you get in, can get all items for free. For any bidder, have 1/log chance of getting within factor of 2 of its max valuation. Can we do this via Item Pricing?
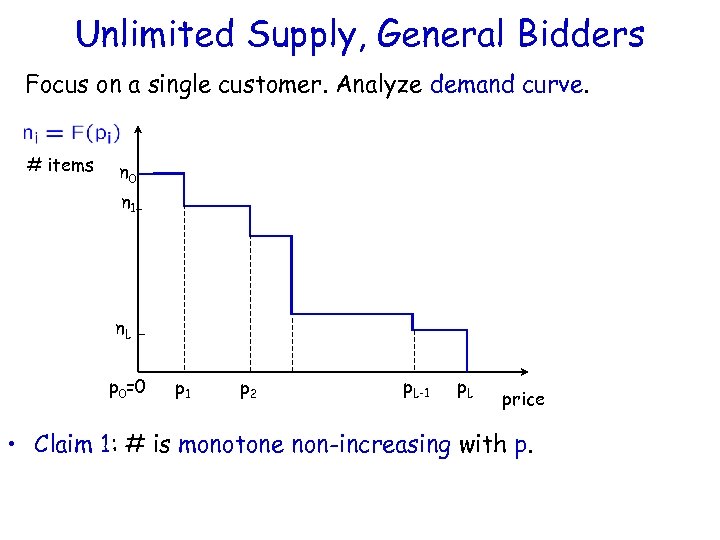
Unlimited Supply, General Bidders Focus on a single customer. Analyze demand curve. # items n 0 n 1 - n. L p 0=0 p 1 p 2 p. L-1 p. L price • Claim 1: # is monotone non-increasing with p.
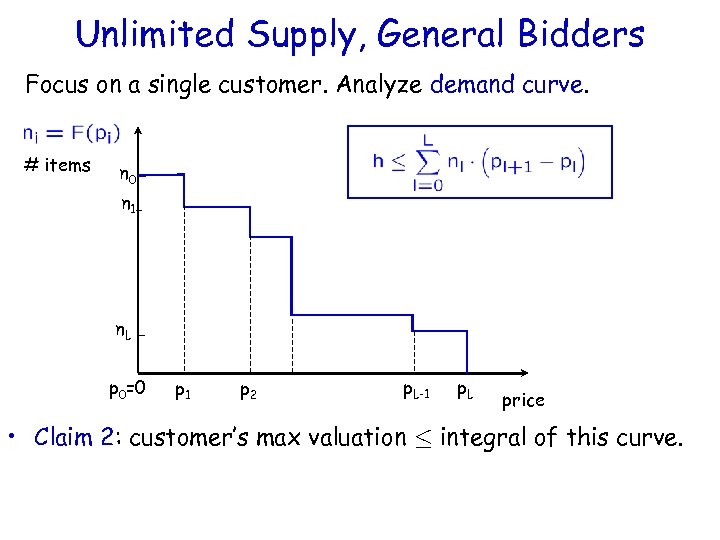
Unlimited Supply, General Bidders Focus on a single customer. Analyze demand curve. # items n 0 n 1 - n. L p 0=0 p 1 p 2 p. L-1 p. L price • Claim 2: customer’s max valuation · integral of this curve.
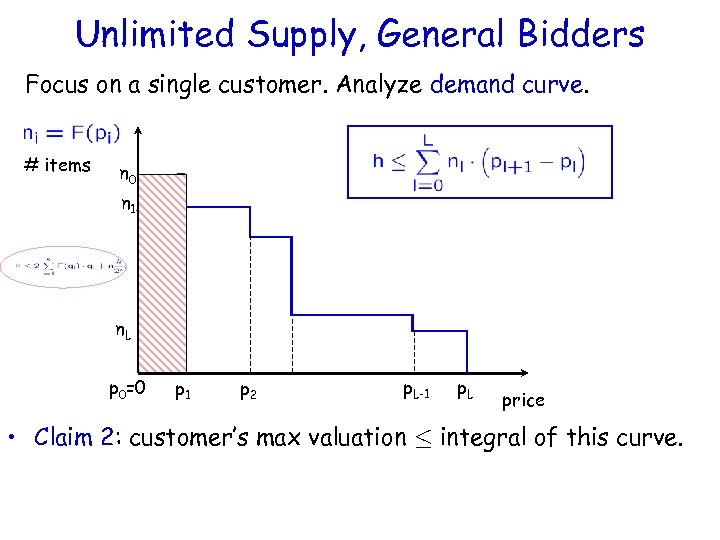
Unlimited Supply, General Bidders Focus on a single customer. Analyze demand curve. # items n 0 n 1 - n. L p 0=0 p 1 p 2 p. L-1 p. L price • Claim 2: customer’s max valuation · integral of this curve.
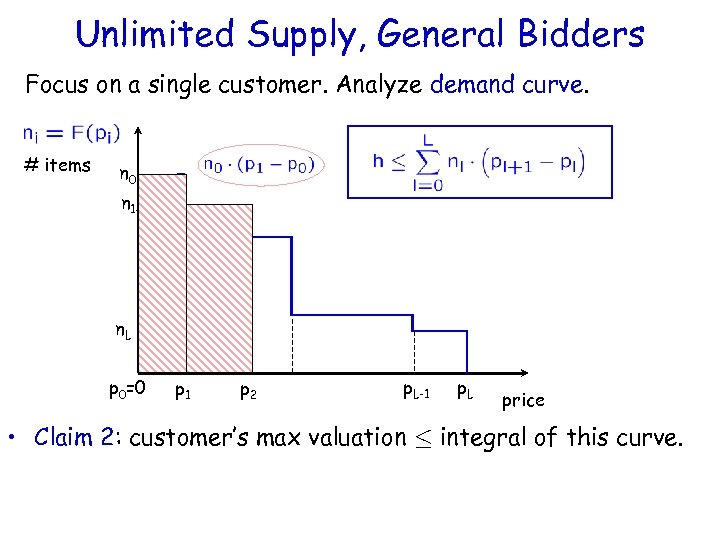
Unlimited Supply, General Bidders Focus on a single customer. Analyze demand curve. # items n 0 n 1 - n. L p 0=0 p 1 p 2 p. L-1 p. L price • Claim 2: customer’s max valuation · integral of this curve.
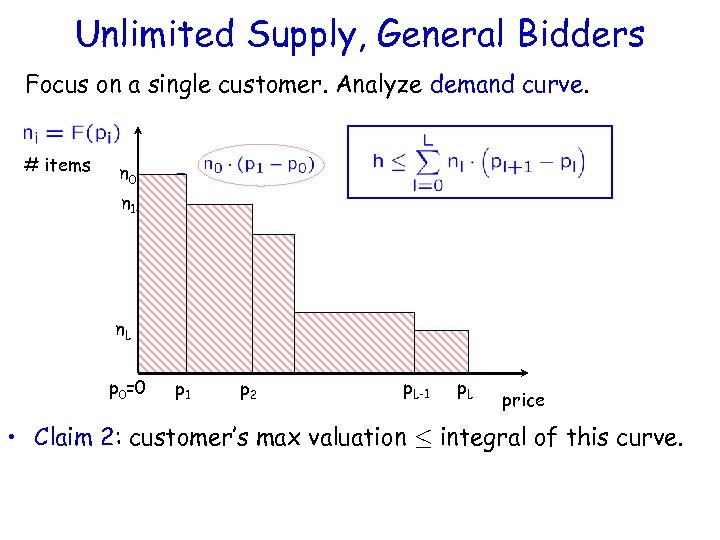
Unlimited Supply, General Bidders Focus on a single customer. Analyze demand curve. # items n 0 n 1 - n. L p 0=0 p 1 p 2 p. L-1 p. L price • Claim 2: customer’s max valuation · integral of this curve.
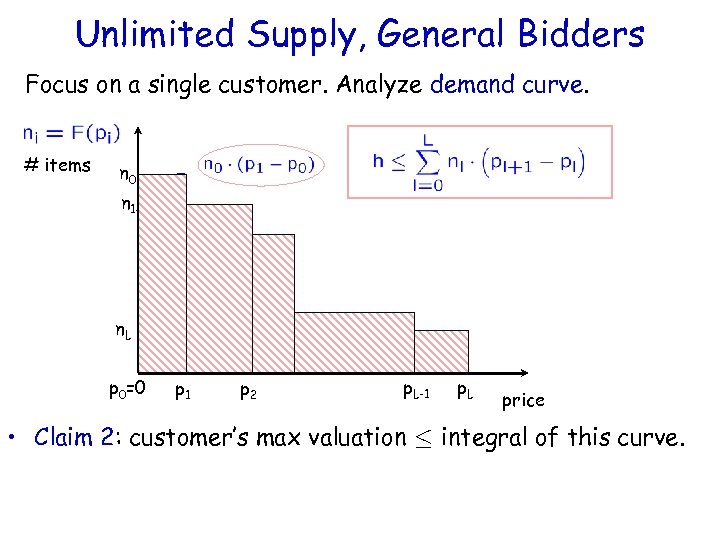
Unlimited Supply, General Bidders Focus on a single customer. Analyze demand curve. # items n 0 n 1 - n. L p 0=0 p 1 p 2 p. L-1 p. L price • Claim 2: customer’s max valuation · integral of this curve.
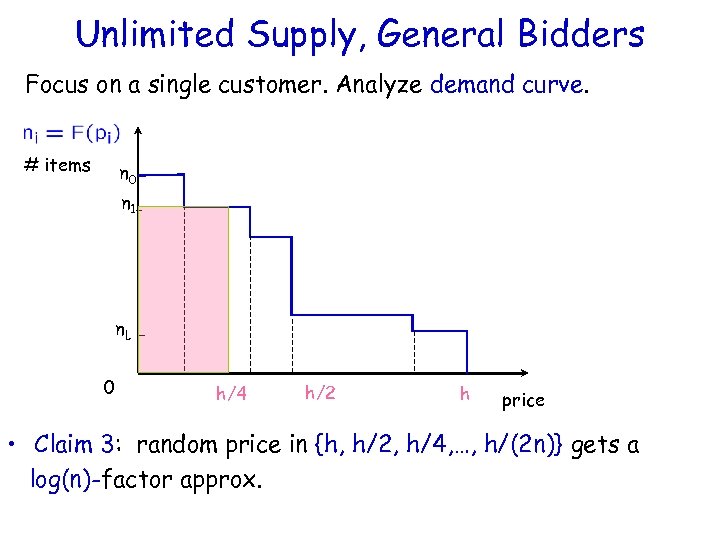
Unlimited Supply, General Bidders Focus on a single customer. Analyze demand curve. # items n 0 n 1 - n. L 0 h/4 h/2 h price • Claim 3: random price in {h, h/2, h/4, …, h/(2 n)} gets a log(n)-factor approx.

What about the limited supply setting?

What about Limited Supply? Assume one copy of each item. Goal: Profit Maximization Fixed Price (p): Set R=J. For each bidder i, in some arbitrary order: • Let Si be the demanded set of bidder i given the following prices: p for each item in R and for each item in JR. • Allocate Si to bidder i and set R=R Si. Assume bidders with subadditive valuations.

Limited Supply, Subadditive Valuations There exists a single price mechanism whose profit is a approximation to the social welfare. Can show a lower bound, for =1/4. Other known results: welfare & revenue [DNS’ 06] show a approximation to the total welfare for bidders with general valuations. welfare [DNS’ 06], [D’ 07] show that a single price mechanism provides a logarithmic approx. for social welfare in the submodular, subadditive case.

A Property of Subadditive Valuations Lemma 1 Assume vi subadditive. Let (T 1, …, Tm) be feasible allocation. There exists (L 1, …, Lm) and a price p such that : (1) (2) (L 1, …, Lm) is supported at price p. Li the subset that bidder i buys in a store where he sees only Ti and every item is priced at p.

Subadditive Valuations, Limited Supply Lemma 1 Let (T 1, …, Tm) be feasible allocation. 9 (L 1, …, Lm) and price p such that : and (L 1, …, Lm) is supported at price p. Lemma 2 Assume (L 1, …, Lm) is supported at p and let (S 1, …, Sm) be the allocation produced by Fixed. Price (p/2). Then: Theorem • There exists a single price mechanism whose profit is a approximation to the social welfare.

Conclusions and Open Problems Summary: • Item Pricing mechanism for limited supply setting. • Matching upper and lower bounds. Open Problems • Better revenue maximizing mechanisms for the limited supply?

c920f0dee48f3b4548024dc08c5e21b4.ppt