eba533470eb52d9bafb9b8bdc013049a.ppt
- Количество слайдов: 154

It’s the…

• You remember this! It’s just: • • • Seems simple? It is!! Just remember that you have to factor out “h” from the numerator so that it cancels with the denominator, and you’re set. – Unfortunately, teachers/exam writers know it’s easy so they make this factoring process really (really!)hard.

Try an Example Start with the function Input it into the rule Expand the factorial Now you have to factor out h… And apply the limit! Remember: h cannot =0 but it gets SO CLOSE we just can ignore it!

Need MORE Pra. CTi. CE? • Don’t be fooled – this powerpoint makes first principles simple and, while the concept is, the test questions can really do test your factoring abilities. • Pointers: – You may be left with “h”s all over after factoring it out – as long as none are denominators, you should be ok! • Practice: HL Math Book page 316 (example) – Questions on page 321… try with first principles!

Power Rule, Chain Rule, & Implicit Differentiation Peter Tu IB Math HL (C)

Power Rule • The power rule comes into effect for differentiation for equations who are in the form, a being a constant, x the variable, and n also a constant: • From the method of first • Hence, the power rule principles, we find that: states:

Example • Since it is possible to actually split up different terms during differentiation, • We can use this to differentiate the equation: • In the following fashion:

Chain Rule • What should we do if we have to differentiate a function respective to another function? • Given x, y, and z, can we differentiate x relative to z indirectly? • If we write the differential as: • Since a differential is defined as the small change of one over the small change of the other, we can apply a multiplication rule of fractions for the chain rule:

Example • The factory produces cups modeled by function: • These cups in turn generate revenue modeled by the function: • What is the rate of revenue generated?

Further exploration • Note, that the chain rule has no limits on how many elements it can have, since it is really based on multiplication of fractions, so it is possible to have:

Implicit Differentiation • What happens when we try to differentiate a relationship between two variables that are no given as explicit functions? • Take: • Implicit functions are dealt with the same way, by differentiating each term with respect to one variable, in this case x:

• Then, by using the chain rule and product rules, we can simplify the equation: • Then we move the terms with the differential of y in respect to x to one side, and factor:

Further Example • Consider a simpler case: • The concept is the same:

Product Rule Function Derivative

Differentiate the following: Let y = so that u = x² and v = sin (x) This means that and = 2 x This time set up a table: T h function derivative i s = cos (x). Using the product rule we have that Adding, we have:

Quotient Rule Function Derivative

Differentiate the following: Let u = x² + 1 and v = sin (x) This gives the following derivatives, and Using the quotient rule we have:

Differentiation of Trig. Functions

Examples

DIFFERENTIATION Log and Euler Functions

Differentiation of Log Functions NOTE! The derivative of the natural log of any value nx, example: ln 5 x, is equal to 1 over x!
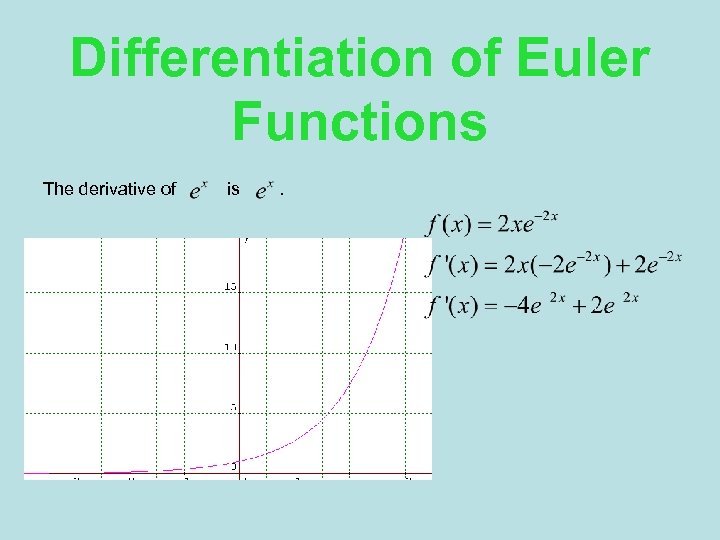
Differentiation of Euler Functions The derivative of is .

Jessie Chiang Block C

Tangents and Normals Finding Tangents: (the line that touches a point on a function and shares the slope of the point on the function) 1. FIND THE SLOPE OF THE TANGENT (slope of tangent at (x, y) will be f’(x) at x) 2. PLUG THE SLOPE (m) INTO LINEAR EQUATION y= mx+b 3. PLUG ORIGINAL POINTS (x, y) INTO LINEAR EQUATION TO FIND b 4. DONE!!

Tangents and Normals • Finding Normals: (the perpendicular line to a point on a function) 1. FIND THE SLOPE OF THE TANGENT (slope of tangent at (x, y) will be f’(x) at x) 2. REMEMBER THAT LIKE ALL PERPENDICULAR LINES, THE SLOPE OF THE NORMAL X THE SLOPE OF THE TANGENT = -1. 3. USE SLOPE OF TANGENT TO GET SLOPE OF PERPENDICULAR 4. PLUG THE SLOPE (m) INTO LINEAR EQUATION y= mx+b 5. PLUG ORIGINAL POINTS (x, y) INTO LINEAR EQUATION TO FIND b 6. DONE!!
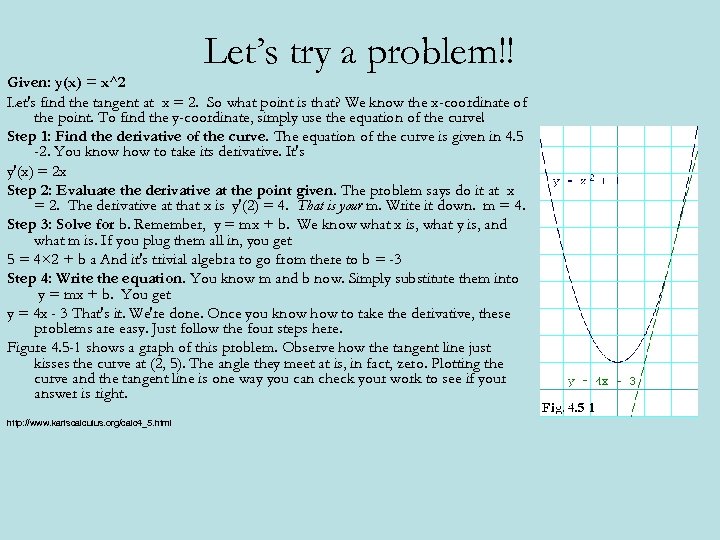
Let’s try a problem!! Given: y(x) = x^2 Let's find the tangent at x = 2. So what point is that? We know the x-coordinate of the point. To find the y-coordinate, simply use the equation of the curve! Step 1: Find the derivative of the curve. The equation of the curve is given in 4. 5 -2. You know how to take its derivative. It's y'(x) = 2 x Step 2: Evaluate the derivative at the point given. The problem says do it at x = 2. The derivative at that x is y'(2) = 4. That is your m. Write it down. m = 4. Step 3: Solve for b. Remember, y = mx + b. We know what x is, what y is, and what m is. If you plug them all in, you get 5 = 4× 2 + b a And it's trivial algebra to go from there to b = -3 Step 4: Write the equation. You know m and b now. Simply substitute them into y = mx + b. You get y = 4 x - 3 That's it. We're done. Once you know how to take the derivative, these problems are easy. Just follow the four steps here. Figure 4. 5 -1 shows a graph of this problem. Observe how the tangent line just kisses the curve at (2, 5). The angle they meet at is, in fact, zero. Plotting the curve and the tangent line is one way you can check your work to see if your answer is right. http: //www. karlscalculus. org/calc 4_5. html

Another problem! Let's take our example from before where the curve is y = x^2 + 1 and we want the normal line to pass through (2, 5). Step 1 is the same as before. It is still the case that y' = 2 x. In step 2, though, after we evaluate y'(x) at x = 2 and find that it's equal to 4, instead of setting m to that, we set m to its negative reciprocal, which is -1/4. The remaining steps are the same. Solve for b with the x and y coordinates you have and the m you have just determined. In this case we have: 5 = (-1/4)× 2 + b and solving for b, we have b = 5. 5 So the answer here is y = (-1/4)x + 5. 5 Figure 4. 5 -2 shows a plot of our curve and the line that is normal to it at x = 2. Observe that the normal line crosses our curve in two places. At (2, 5) is the crossing at right angles that we expected to get. To the left there is another crossing at a point we have not determined yet. http: //www. karlscalculus. org/calc 4_5. html
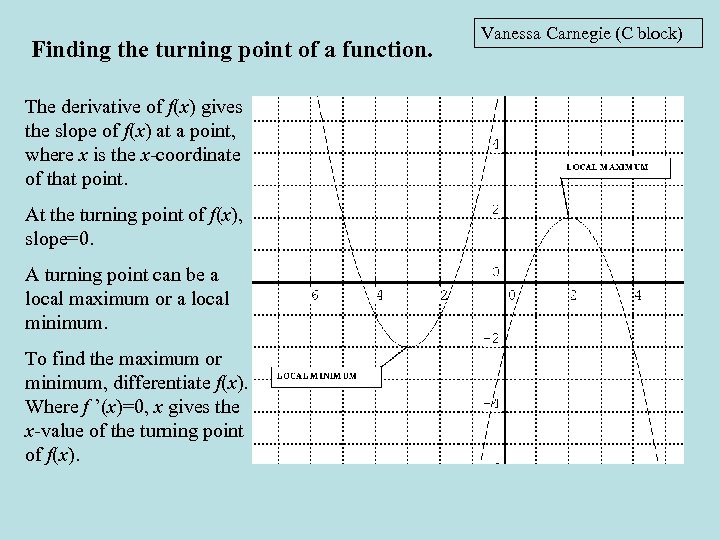
Finding the turning point of a function. The derivative of f(x) gives the slope of f(x) at a point, where x is the x-coordinate of that point. At the turning point of f(x), slope=0. A turning point can be a local maximum or a local minimum. To find the maximum or minimum, differentiate f(x). Where f ’(x)=0, x gives the x-value of the turning point of f(x). Vanessa Carnegie (C block)
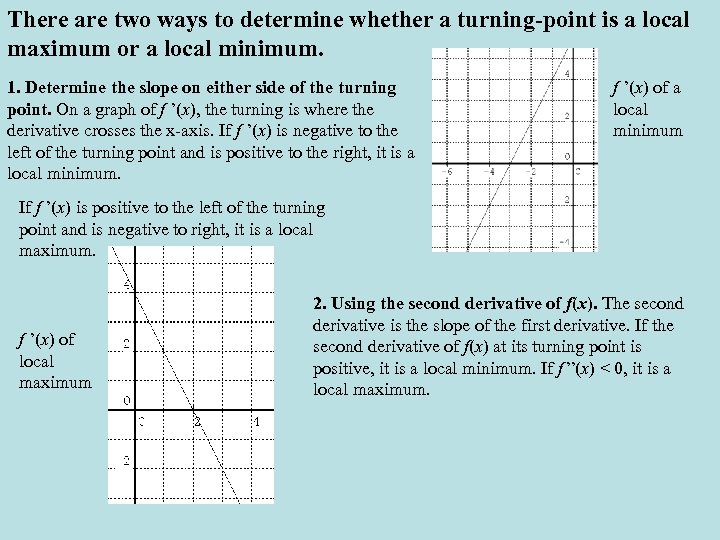
There are two ways to determine whether a turning-point is a local maximum or a local minimum. 1. Determine the slope on either side of the turning point. On a graph of f ’(x), the turning is where the derivative crosses the x-axis. If f ’(x) is negative to the left of the turning point and is positive to the right, it is a local minimum. f ’(x) of a local minimum If f ’(x) is positive to the left of the turning point and is negative to right, it is a local maximum. f ’(x) of local maximum 2. Using the second derivative of f(x). The second derivative is the slope of the first derivative. If the second derivative of f(x) at its turning point is positive, it is a local minimum. If f ”(x) < 0, it is a local maximum.

And now for an example… An open rectangular box with square base is to be made from 48 ft. 2 of material. What dimensions will result in a box with the largest possible volume ? Find an equation for the surface area of the box. Rearrange this to solve for y. Now, find an equation for the volume of the box. Replace y in so that x is the only variable.

To find the maximum volume for the box, differentiate V and let it equal zero. Solve for x. To verify our answer, find the second derivative for the volume. At x=4, This confirms that there is a local maximum at x=4. (x cannot be a negative value because it represents a length. ) Now we can find y. The dimensions that will result in a box with the largest possible volume are: Example taken from http: //www. math. ucdavis. edu/~kouba/Calc. One. DIRECTORY/maxmindirectory/Max. Min. html (full of applied maximum/minimum problems)

Maximum and Minimum Word Qu 3 stions Jason L 3 i

Max / Minimum Word Questions • Application of calculus to find maximums or minimums • Example – The points PQR form the corner of a house, where angle PQR is a right angle. Running parallel to these walls is a garden patch. 20 meters of fencing is available to create an enclosure PUTSRQ, in such a way that PU = RS = x. Assume PQ = QR = y.

Example (continued): How should the fencing be placed so that area PQRSTU is a maximum? We know total fencing = 20 m 2(y+x)+2 x=20 2 y+4 x=20 1. 2 y = 20 – 4 x Area = 2(x*y) + x^2 = x^2 + 2 xy Sub 1. Into this equation = x^2 + 20 x - 4 x^2 = 20 x – 3 x^2

Example(continued) We know A = 20 x – 30 x^2 Using the first derivative we can find the x value that will give a maximum Area f’(x) = 20 – 60 x = 20 x=1/3 Let f’(x) = 0 Still we need to check if this is a maximum, minimum or point of inflexion For x values lower than 1/3, f’(x) is + For x values higher than 1/3, f’(x) is – Therefore it is a maximum point!!!

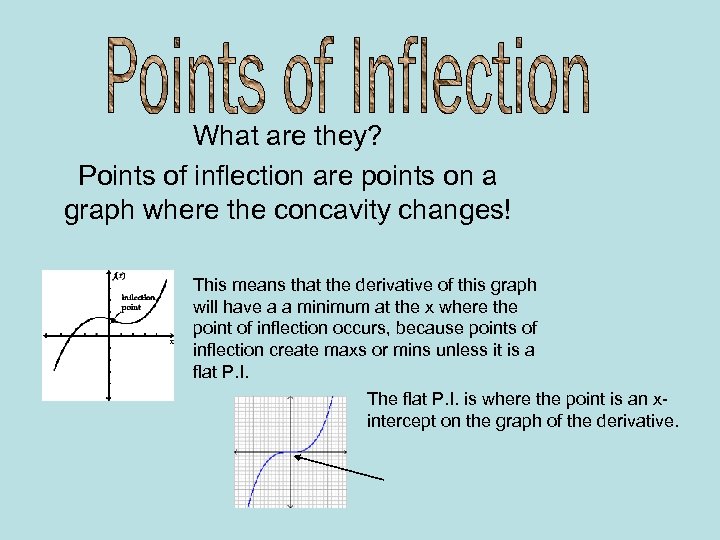
What are they? Points of inflection are points on a graph where the concavity changes! This means that the derivative of this graph will have a a minimum at the x where the point of inflection occurs, because points of inflection create maxs or mins unless it is a flat P. I. The flat P. I. is where the point is an xintercept on the graph of the derivative.
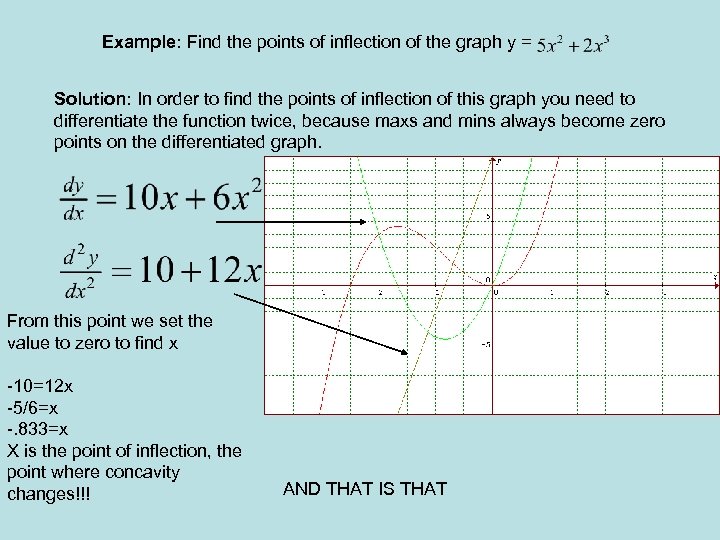
Example: Find the points of inflection of the graph y = Solution: In order to find the points of inflection of this graph you need to differentiate the function twice, because maxs and mins always become zero points on the differentiated graph. From this point we set the value to zero to find x -10=12 x -5/6=x -. 833=x X is the point of inflection, the point where concavity changes!!! AND THAT IS THAT

Related Rates of Change!

Related Rates of Change What’s this all about? • We use related rates to relate the rate of change of one variable with another • Everybody could have their own method of doing these that they are comfortable with! • Generally, start with this when you get a question: – Given: Write what information you have. – Want: What are you looking to find? – When: When! • You need to know your formulae for shapes! – Ex// Volumes and surface areas of spheres, cones, cylinders • Try to visualize each problem!

Let’s do a problem together! Get a pencil and pen! • Air is leaking from a spherical balloon at a rate of 5 cm 3 /min. Fin the rate at which the surface area of the balloon is changing when the radius is 10 cm. • Given: • Want: • When: Good Job!

Integration of LOG and EULER functions By: Cassandra Wee Block G

So…we already know how to do basic integration. Now, we’ll learn how to do it with log and Euler functions! =D For log functions, you want to change the integral into the following form: For Euler functions, you want to change the integral into the following form:

Let’s try to integrate with a log function… REMEMBER: our goal is to get this

Now let’s try a Euler function… REMEMBER: our goal is to get this

Integrating Trig Functions how exciting… Elyn Tan

Integrating trig functions can be tricky… More specifically, let’s look at the cosine double angle rule… This tricky little thing can equate to other tricky little things that can eventually help you solve complex trig functions!!

Example This is a common type of situation where you would need to use the double angle rule… Then, looking at the previous slide, choose the appropriate rule to use. In this case, we should use

And so using that rule we can now integrate the trig function… And so… Here we must use the substitution rule Let

Another example Again, we must use the substitution rule Looks hard? No worries… First begin with this: Let

Differentiation and Integration of Inverse Trigonometric Functions Differentiation of inverse sine: Differentiation of inverse tangent: Differentiate both sides with respect to x But, from the identity: We have:

Differentiation and Integration of Inverse Trigonometric Functions Integration to inverse sine: Integration to inverse tangent: Express in terms of differentials: Integrate both sides:

Differentiation and Integration of Inverse Trigonometric Functions Example 1: By the chain rule: Example 2: Knowing that: We find that:

Integration by Substitution Normal… Integration by Substitution is pretty self-explanatory. Basically, we let something in the original function equal to something new to make the integration easier or work. Consider: First step, we would look for any derivatives of a term in the integral function. We can spot two. derivative is . Then, we choose a term in the integral to be substituted by another easier variable, say u.

In this particular function, we can substitute either term in the integral ( and ) I will substitute Therefore, for u. And… substitute to get Since we derivative Therefore, know. REMINDER: IF INTEGRAL IS DEFINITE, THEN DON’T FORGET TO CHANGE THE BOUNDARIES WITH THE SUBSTITUTED VALUE!!!!! Rearrange it and we get Look at the original equation, there is also We can substitute it for du, forming the equation… Which is much easier than it was at first. Now… You try a question.
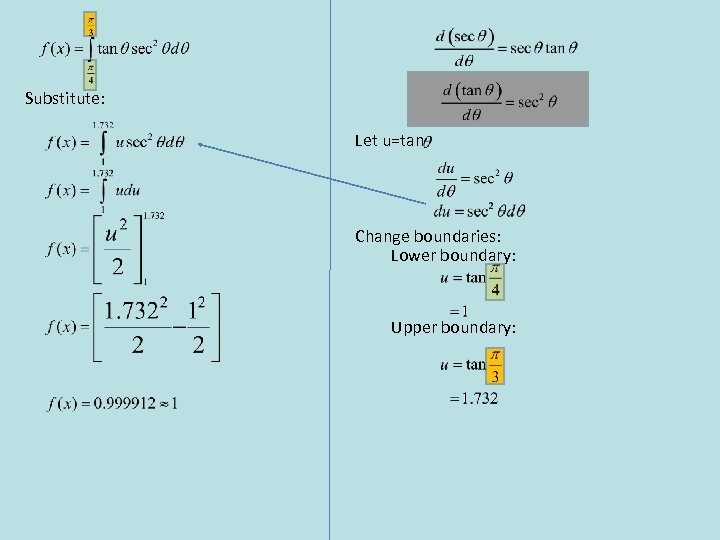
Substitute: Let u=tan Change boundaries: Lower boundary: Upper boundary:

Unusual and Special Substitutions Julian Springer

Integration by Substitution Integration by substitution is used to make the integration process easier. Usually, what needs to be substituted is easy to see, but there are cases where it is not obvious what part of the function needs to be substituted to make the integration easier to solve.

Examples There is a way to solve these problems, but it is not immediately obvious. In the next slide, the substitution will be shown.

The Substitution Function Contains: Substitute: Ex:

Examples Solved Here, the first example is solved: This is the substitution: The final step is done using triangles, and finding what angle theta holds.

Integration by Parts Lena Shen

So what is Integration by Parts? I • Used when the integral contains the product of two functions of x • We know from product rule that: • Therefore:

So what is Integration by Parts? II • Changing the sides, we get: • WHICH IS OUR RULE~ (*^U^)人(≧V≦*)/ • Written in rule book as:

Sample Problem! • Integrate let

INTEGRATION BY PARTS (double) Yung Lam Ho

Integration by parts (double) is when you have to integrate by parts TWICE! PART 1: Now we need to use integration by parts one more time to integrate cosxex!

PART 2:

Differential Equations: • • Used to solve problems in the form: Strategy to solve such problems: Bring all the y-terms and x-terms such that: Example: The dx cancels here so left side becomes only in terms of y and the right side only in terms of x Note: do NOT forget the constant c and simply add a “+ c” at the end of the expression because this would be WRONG! I. e. Would be wrong.

Another example! Step by step: First bring the expression with y on the left side. Then integrate both sides with respect to x. Finish the integration. Re-arrange the equation to make it in terms of y (don’t forget the constant c because this is an indefinite integral) Where which is a constant.

Last example this time with definite integral equations! • • Consider the following expression: = 1, find the definite expression for y. The working out to solve this is shown below: and given that for y = 0, x • Now, at this point, sub in the values given above and solve for c: therefore the y expression is:
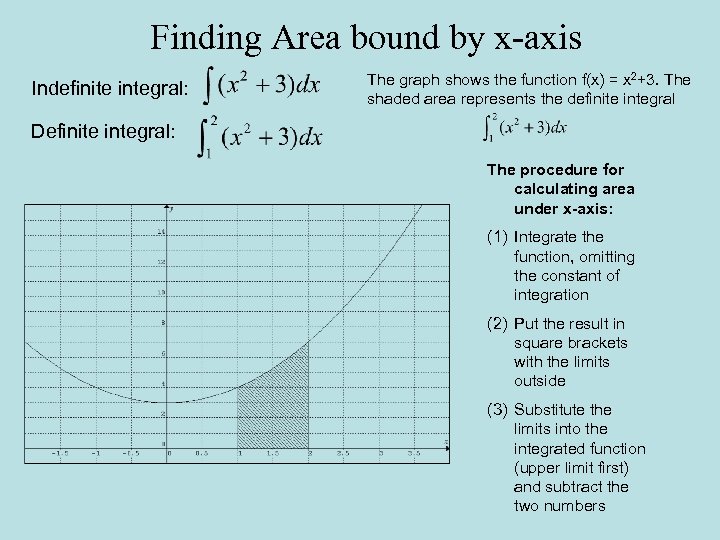
Finding Area bound by x-axis Indefinite integral: The graph shows the function f(x) = x 2+3. The shaded area represents the definite integral Definite integral: The procedure for calculating area under x-axis: (1) Integrate the function, omitting the constant of integration (2) Put the result in square brackets with the limits outside (3) Substitute the limits into the integrated function (upper limit first) and subtract the two numbers
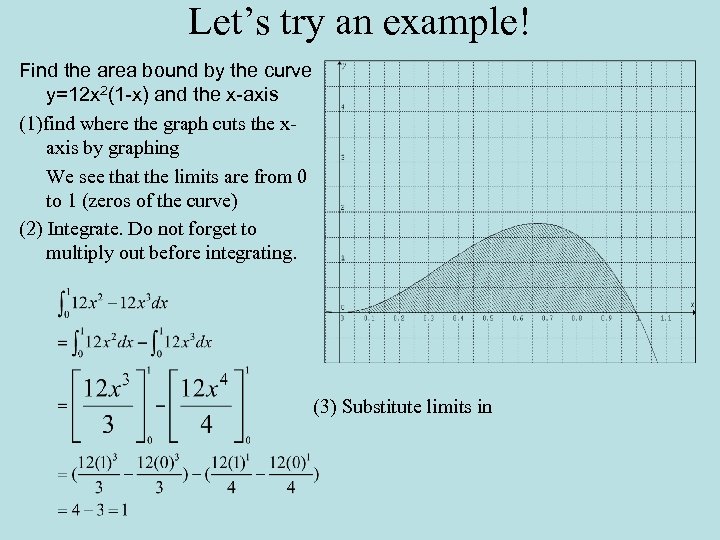
Let’s try an example! Find the area bound by the curve y=12 x 2(1 -x) and the x-axis (1)find where the graph cuts the xaxis by graphing We see that the limits are from 0 to 1 (zeros of the curve) (2) Integrate. Do not forget to multiply out before integrating. (3) Substitute limits in
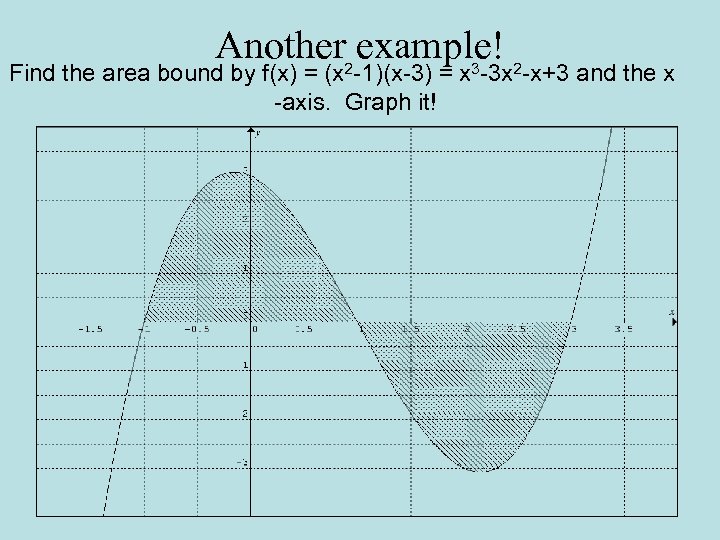
Another example! Find the area bound by f(x) = (x 2 -1)(x-3) = x 3 -3 x 2 -x+3 and the x -axis. Graph it!

We can see from the graph that the limits are from -1 to 1, and 1 to 3. We must be careful here. There is a negative area. You cannot integrate separately and add the two areas. You must subtract the negative area from the positive because we want a positive area!
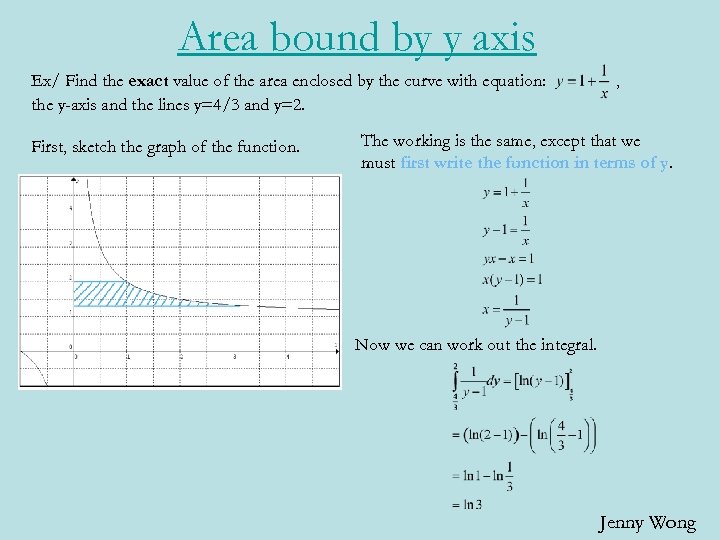
Area bound by y axis Ex/ Find the exact value of the area enclosed by the curve with equation: the y-axis and the lines y=4/3 and y=2. First, sketch the graph of the function. , The working is the same, except that we must first write the function in terms of y. Now we can work out the integral. Jenny Wong

Area Between Two Curves

Boundaries • First, the intersection points between the two graphs needs to be found. To do this, set the two functions to be equal to each other and then solve for x. • These intersection points are the boundaries for the integration. Generally there will only be 2 intersection points, but if there are more, consider the functions to be in different sections. For example, if there are intersection points at x = -2, 2 and 4, then integrate between -2 and then 2 and 4.

What next? • Before you integrate the functions, first find which function is will have a greater area beneath it. To do this, you can simply graph the two functions and see which is further from the axis which you will be integrating from (this will almost always be the x-axis)

Finally integrate • The area bound by the two curves is the difference in the areas beneath each of the curves. This can be done by integrating the difference of the curves. Eg. or • For good examples of how to do it, go to http: //archives. math. utk. edu/visual. calculus/5/ar ea 2 curves. 3/index. html

Volume Around X Axis By: Patrick Bai

Volume Around the X Axis • Consider the region between the graph of a continuous function and the x axis from where x = a to x = b • Take for example where and 2 -D image Revolved around the x axis

Volume Around X Axis • Volume = where • V= Taken from: http: //curvebank. calstatela. edu/volrev. htm

Volume Around Y Axis By: Michael Chang

Volume Around the X Axis • Consider the region between the graph of a continuous function • To find the volume of revolution around the y axis, express the equation in terms of x using y. • Find the limits in terms of y; y = a to y = b • Take for example where and

Volume Around X Axis • Volume = • V=
Volumes of revolution – bound by 2 curves!
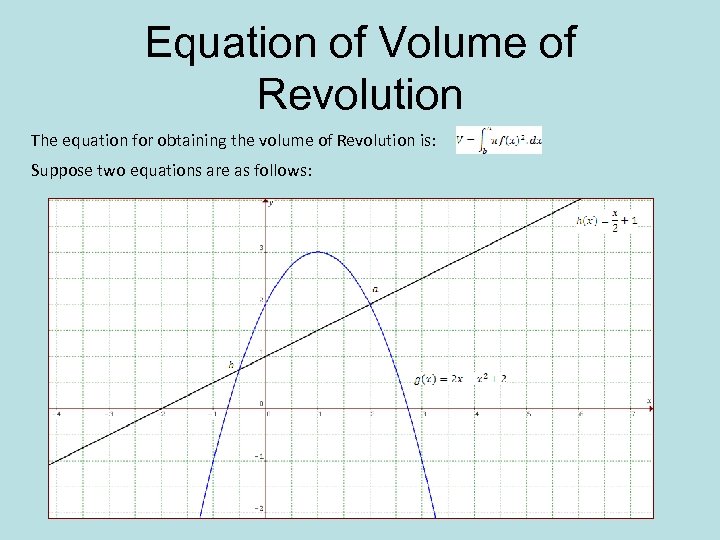
Equation of Volume of Revolution The equation for obtaining the volume of Revolution is: Suppose two equations are as follows:

Calculations First find the intersection points (a, b) by equating the two curves: After calculating the intersection you will find: , ) Second find plug the functions into the equation: It’s g(x) – h(x) because g(x) is on top! *Note* Remember to graph the functions so you can see which is on top The equation can then be worked out: We can then use the fn. Int (f(x), x, a, b) function to figure out the volume = π ( 15. 46875 – 5. 0520833) = π (10. 4167) = 125 π/12 units 3


Calculus Test#1 7. Find the total area enclosed by the function and the x-axis. Graph the function on the calculator. It shows that area between x=1 and x=1 has a positive yvalue and areas between x=1 and x=2, and between x=1 and x=-2 have negative y-values. While integrating, set up the equation so that there’s a negative sign in front of areas with boundaries that have negative y-values.
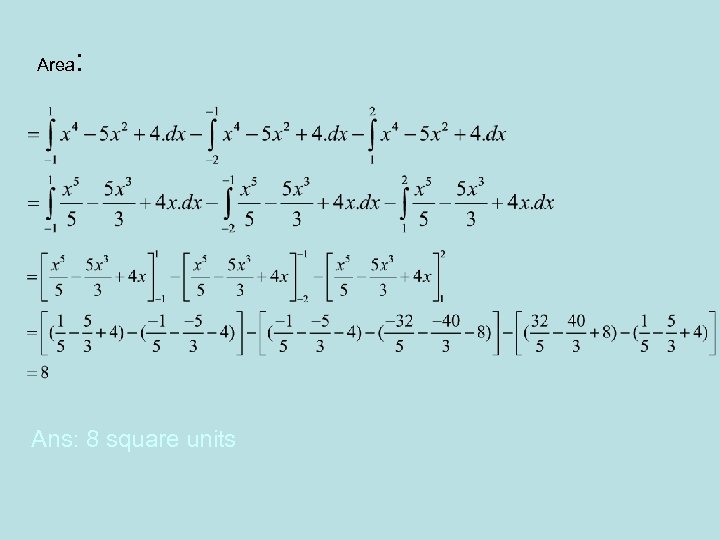
Area : Ans: 8 square units

8. The shaded area shown below the function is 6 a units. Find a. Integrate the given equation using a and -a as boundaries
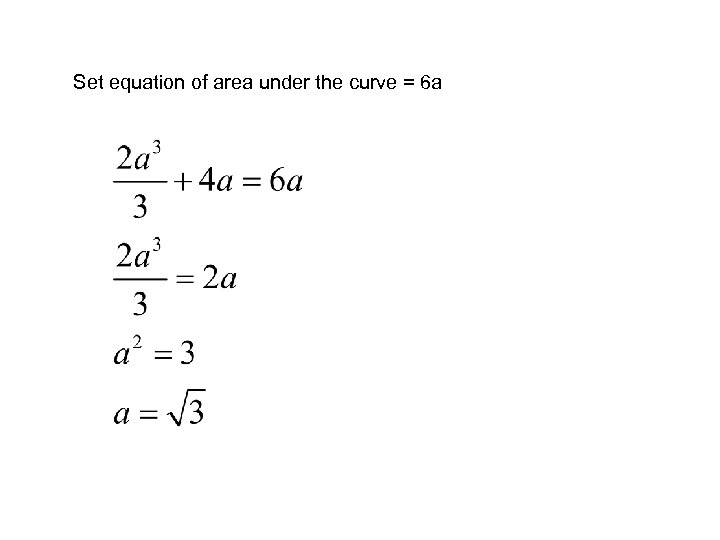
Set equation of area under the curve = 6 a

By Robert Xie

The beginning…

Cont. .

It cannot yet be determined whether it is a maximum point. Thus, we use the second derivative. If the value is greater than zero, it is a minimum; if it is less than zero, it is a maximum.

ii) To find the coordinates iii) Inflection occurs when of the maximum, we the second derivative of substitute the x value f(x) is equal to zero into the original f(x) function.

c) To find the area bound by the x axis, function f and x=5, the intersection between the function and the x axis must be found Therefore the limits are x=1 and x=5.

To integrate, the substitution rule will be used.

d) Finding the volume can be done using the calculator since the question does not ask for an exact answer.


Semester 2 Exam #3
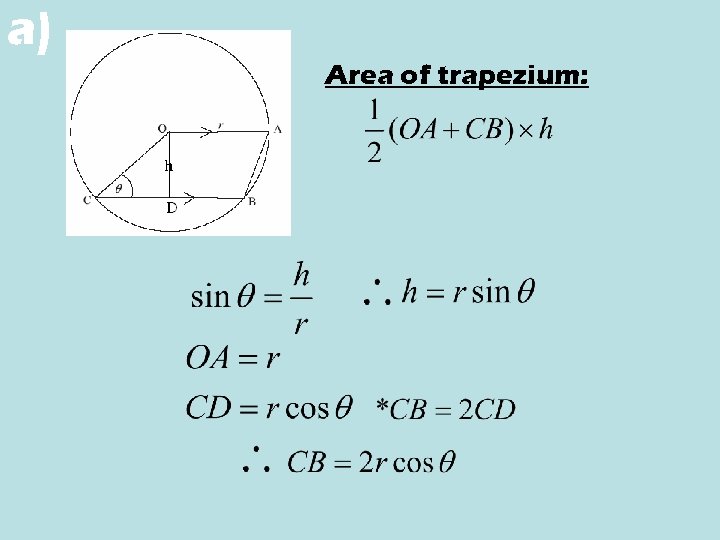
a) Area of trapezium:
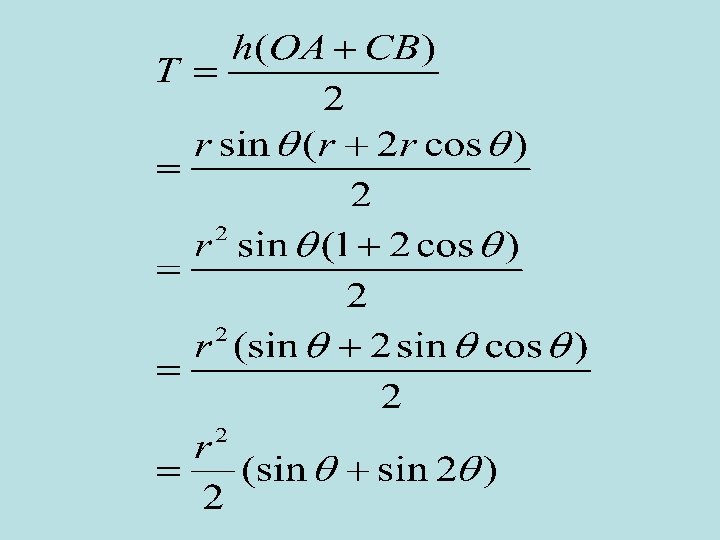

b) differentiate
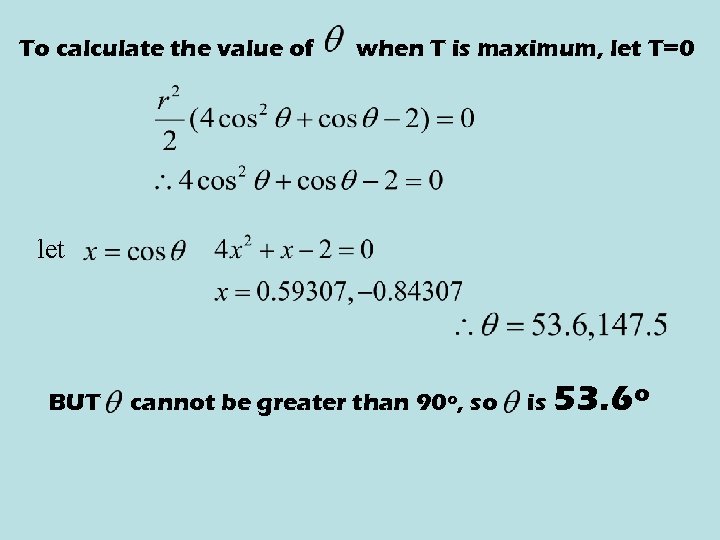
To calculate the value of when T is maximum, let T=0 let BUT cannot be greater than 90º, so is 53. 6º

Verify! x f(x) x<53. 6 f’(x)>0 x>53. 6 f‘(x)<0 Maximum when x=53. 6º

c) Using Cosine Rule:

Parameter = OA+OC+CB+AB = r + 1. 18 r + 0. 902 r 75 cm = 4. 08 r r = 18. 4 cm T is maximum when

Question 6 from 2006 Calculus Exam #2 Given the two functions, and where x and is an angle in radians, find (a) The exact area bound by the two curves and the y axis. (6 marks) (b) The exact volume of the solid generated when the area found in part (a) is rotated fully around the x axis. (6 marks) Yujin Park
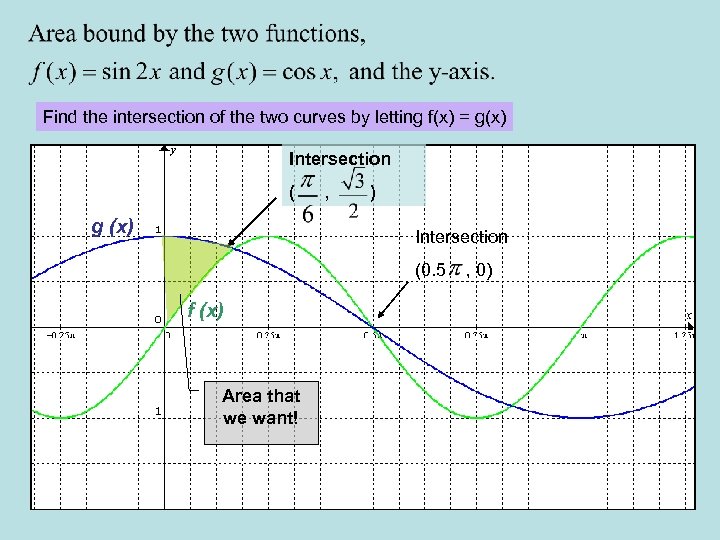
Find the intersection of the two curves by letting f(x) = g(x) Intersection ( g (x) , ) Intersection (0. 5 f (x) Area that we want! , 0)

(a) The exact area bound by the curves and the y axis.
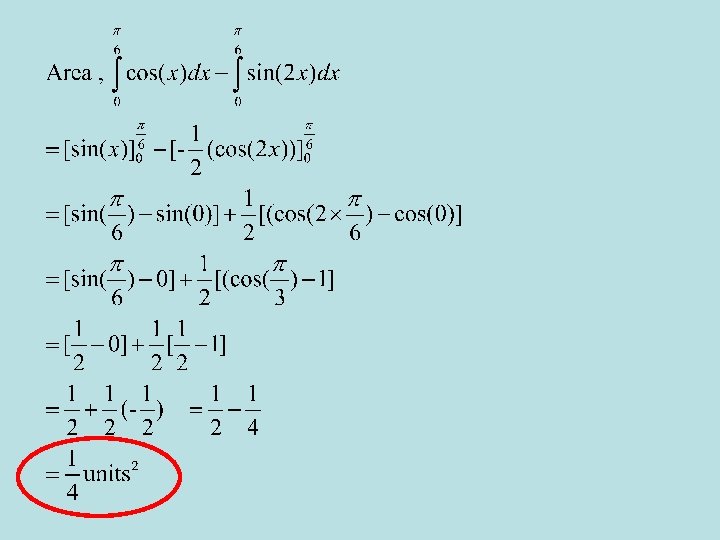

(b) The exact volume of the solid generated when the area found in part (a) is rotated fully around the x axis.


• Question 1. • (Hint: a calculator may be used for (b) and (c) but give some explanation as to how you solved it)

Solution!

Cont…

Question 2. Air is leaking from a spherical balloon at a rate of 5 cm 3/min. Find the rate at which the surface area of the balloon is changing when the radius is 10 cm.

Solution

Cont… Thus area is changing at -1 cm^2/sec when r = 10

Calculus Test #1 Q 9 To make it easier, we’ll rename the functions f(x) and g(x). (a) On the same set of axis, sketch the curves and find the intersection points. (-0. 632, 0. 8) (0. 632, 0. 8) That’s easy, the question doesn’t ask for exact values; just find them on your calculator: (-0. 632, 0. 8) (0. 632, 0. 8)

(b) Find the exact volume of revolution formed when the region enclosed by the curves in (a) is rotated about the y axis. Ok, so we can’t really find the volume around the y axis… We have to rewrite the functions in terms of y so that we can find the volume of revolution around the x axis:
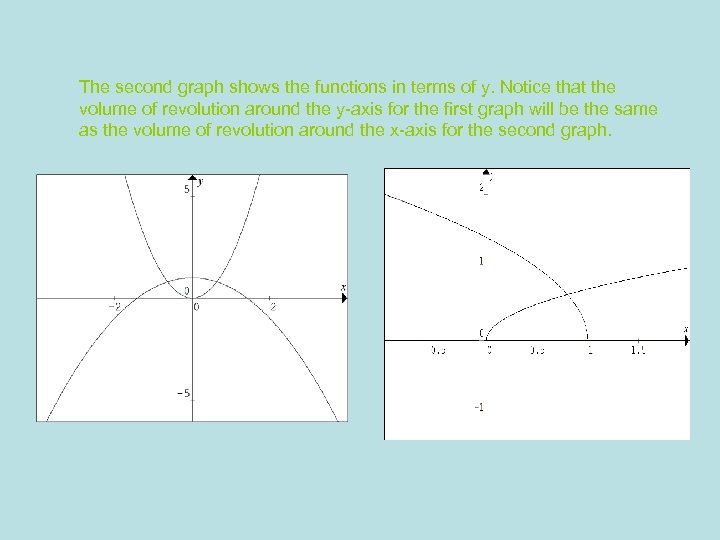
The second graph shows the functions in terms of y. Notice that the volume of revolution around the y-axis for the first graph will be the same as the volume of revolution around the x-axis for the second graph.
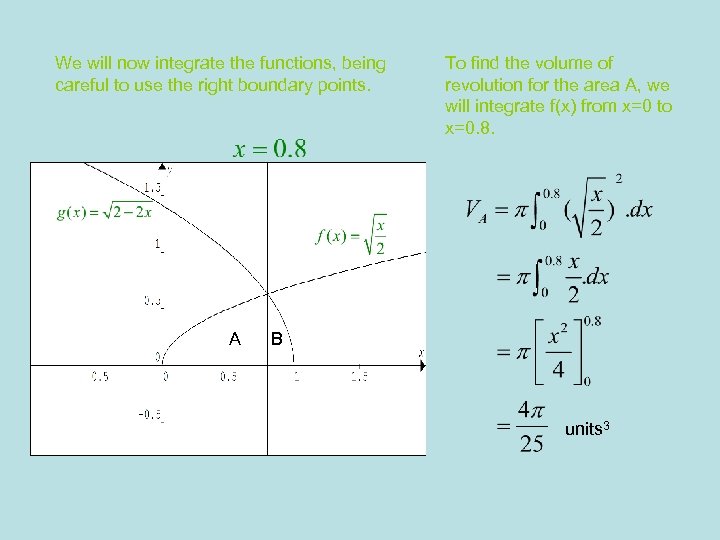
We will now integrate the functions, being careful to use the right boundary points. A To find the volume of revolution for the area A, we will integrate f(x) from x=0 to x=0. 8. B units 3
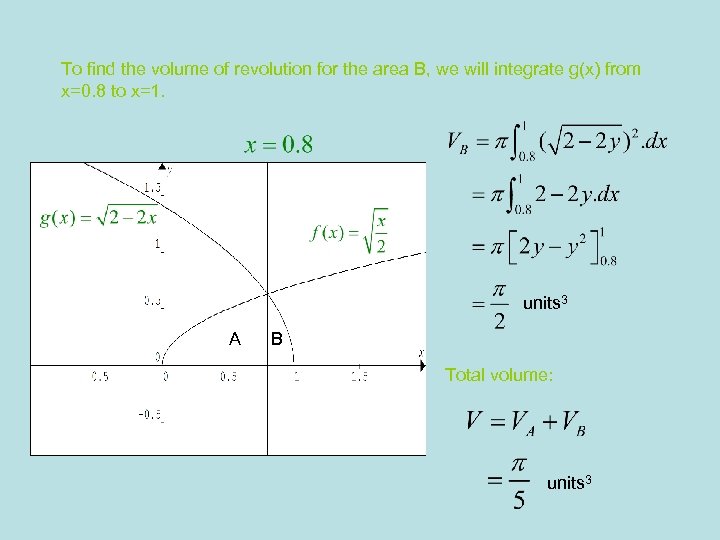
To find the volume of revolution for the area B, we will integrate g(x) from x=0. 8 to x=1. units 3 A B Total volume: units 3

(c) Write an integration equation involving only a single integral that could be used to find the volume of revolution if the region described in (a) is rotated about the x axis. The exact value of the intersection point 0. 632 from (a) can be stored on your calculator and used as the boundary points for the integration. Note the area revolved is g(x) – f(x). (-0. 632, 0. 8) (0. 632, 0. 8)

Madeleine Ong Block C; Math HL II Armstrong

A curve has equation Find the equation of the tangent to this curve at the point (1, 1) Step 1: Find the slope of the tangent formula is the derivative of the given function

Cont… Step 2: Use the slope-intercept form to find the equation of the tangent

Step 1: Establish what rate(s) is known and needs to be found

Cont… Step 2: Manipulate equations to find the rate

Cont…


Test #2 Short Answers 5 and 6 Richard Yeung

Short Answer #5

Part a

Part b

Short Answer #6
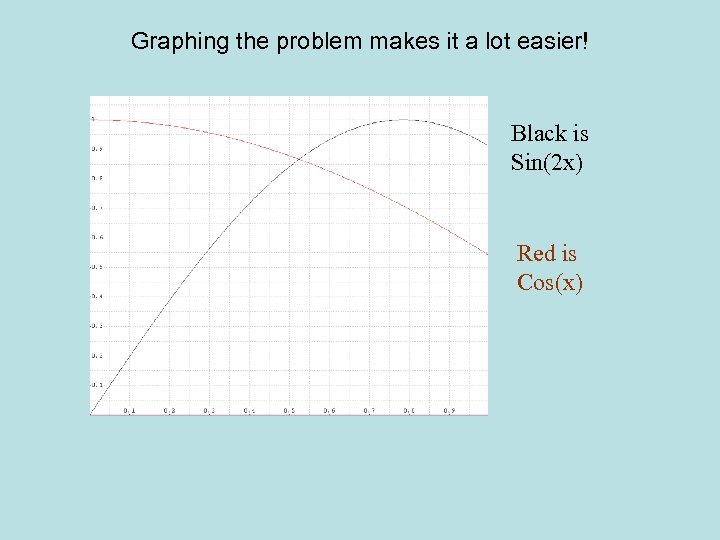
Graphing the problem makes it a lot easier! Black is Sin(2 x) Red is Cos(x)
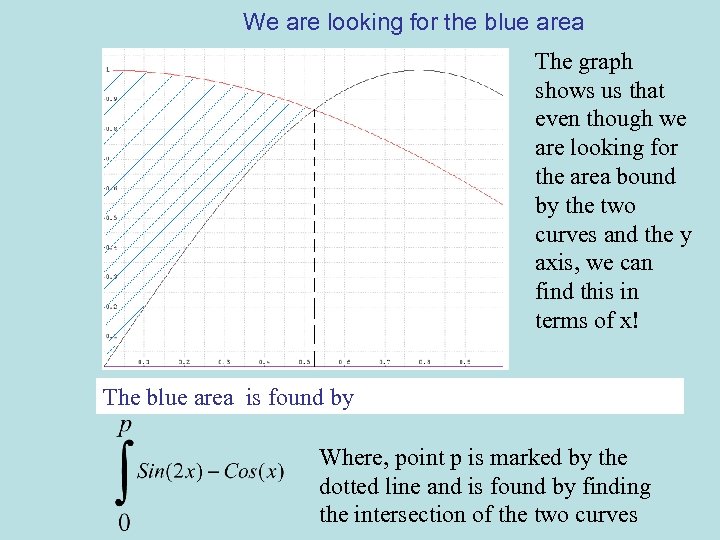
We are looking for the blue area The graph shows us that even though we are looking for the area bound by the two curves and the y axis, we can find this in terms of x! The blue area is found by Where, point p is marked by the dotted line and is found by finding the intersection of the two curves

Finding Intersect • Let – Sin(2 x) = Cos(2 x) – 2 Sin(x)Cos(x) = Cos(x) – Sin(x) = 0. 5 – Think of the 30 -60 -90 triangle –X=

Finding area • We know that p = • Now we must find the area using

Solve • We know that = = = Let u = Cos(x) = Then du = -Sin(x). dx = = 0. 433


g x x


Calculus Test #1 Numbers 3 and 4 Solutions!!

3. The tangent to the curve y = 2 x²+ax+b at the point (-2, 11) is perpendicular to the line 2 y = x + 7. Find the value of a and b • DIFFERENTIATE y = 2 x²+ax+b • y’ = 4 x+a (This is now the slope) • The slope • 2 y = x+7 • y= • Here we can see that the slope equals • ATTENTION! The question asked for. . Perpendicular, thus meaning that the slops is a negative reciprocal • 4 x+a = -2, where x = -2 • a=6

Number 3 continued • Now that we’ve found (a), substitute a=6 into the original equation • y = 2 x²+6 x+b • Now substitute in the point given (-2, 11) to find b • 11 = 2(-2)²+6(-2)+b • 11 = 8 -12+b • b = 15 • So yeay!! Now we’ve found a AND b • a=6 • b = 15

4. Given the sketch below (a) If the line represents y = f(x) give the approximate x values for when (i) f’(x) = 0 ………………………. . (ii) f’’(x) = 0 ……………………. . . • When the first derivative equals zero, you look for the maximum and minimum of the graph – • Thus -5. 5, -1/4, and 4(1/4) When the second derivative equals zero, you look for the x intercepts – Thus -1 and 2

(b) If the line represents y = f’’(x) write the approximate x values where (i) y = f(x) has minimum points …………………. (ii) y = f(x) has maximum points ………………… (iii) y = f(x) has points of inflection ……………… • Since the second derivative is zero, the steps have to be taken backwards to solve this problem. • Use the x intercepts of y = f’’(x) to construct the first derivative graph since they will be the maximum and minimum points • Now use the x intercepts of y = f’(x) to construct the original graph of y = f(x). • Answers – (i) x = -1 – (ii) x = 2 – (iii) x = -5. 5, -1/4, 4
eba533470eb52d9bafb9b8bdc013049a.ppt