История и способы доказательства Теоремы Пифагора Выполнил работу

История и способы доказательства Теоремы Пифагора Выполнил работу ученик 9 класса Мацевич Константин. Руководитель Лытина О. В. Новосибирск 2012

Содержание • Посмотреть, в чем кроется популярность великого математика Пифагора; • История создания теоремы; • Формулировка теоремы; • Разобраться в разных способах доказательства теоремы; • Рассмотреть область ее применения; • Значение теоремы Пифагора.

Биография Пифагора • Великий ученый Пифагор родился в 570 г. до н. э. на острове Самосе. Отцом Пифагора был резчик по драгоценным камням. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Неугомонному воображению юного Пифагора очень скоро стало тесно на маленьком Самосе, и он отправился в Милет, где встретился с другим великим ученым – Фалесом, который посоветовал ему отправиться за знаниями в Египет, что Пифагор и сделал, где изучил язык и религию египтян.

История создания теоремы • Долгое время считали, что до Пифагора эта теорема не была известна. В настоящее время установлено, что эта величайшая теорема встречается в вавилонских текстах, написанных за 1200 лет до Пифагора. Сегодня теорема Пифагора обнаружена в египетском треугольнике в папирусе времен фараона Аменемхета и в древнеиндийском трактате. В древнейшем китайском трактате, утверждается, что китайцы знали свойства египетского треугольника, а к VI в. до н. э. —и общий вид теоремы. • Не смотря на все это, сегодня принято считать, что Пифагор дал первое доказательство носящей его имя теоремы. Увы, от этого доказательства также не сохранилось никаких следов.

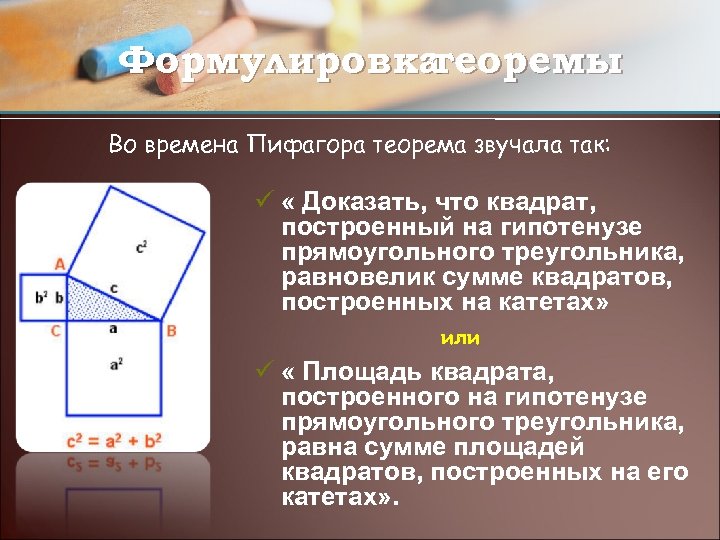
Формулировка теоремы Во времена Пифагора теорема звучала так: ü « Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах» или ü « Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах» .

Пифагоровы тройки • c 2=a 2+b 2 a 3 5 6 7 9 11 13 15 17 19 b 4 12 8 24 40 60 84 112 144 180 c 5 13 10 25 41 61 85 113 145 181 Они обладают рядом интересных особенностей: один из «катетов» должен быть кратным трём; один из «катетов» должен быть равен четырём; Одно из пифагоровых чисел должно быть кратно пяти.

Способы доказательства теоремы Пифагора • Существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и др. ). • Все доказательства делятся на несколько групп: через площадь, через аксиомы, через подобные треугольники, «экзотические» (например, с помощью дифференциальных уравнений), с помощью дополнения или разложения чертежа…

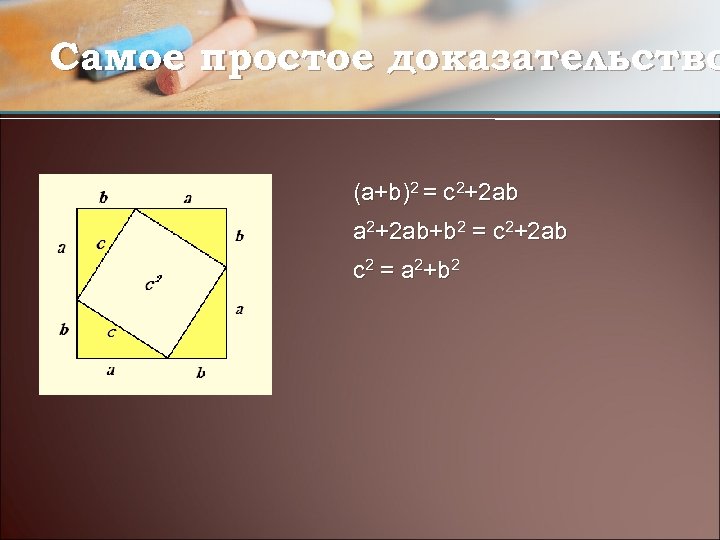
Самое простое доказательство (a+b)2 = c 2+2 ab a 2+2 ab+b 2 = c 2+2 ab c 2 = a 2+b 2

Векторноедоказательство Пусть АВС - прямоугольный треугольник с прямым углом при вершине С, построенный на векторах. Тогда справедливо векторное равенство: b+c=a откуда имеем c=a-b возводя обе части в квадрат, получим c²=a²+b²-2 ab Так как a перпендикулярен b, то ab=0, откуда c²=a²+b² или c²=a²+b²

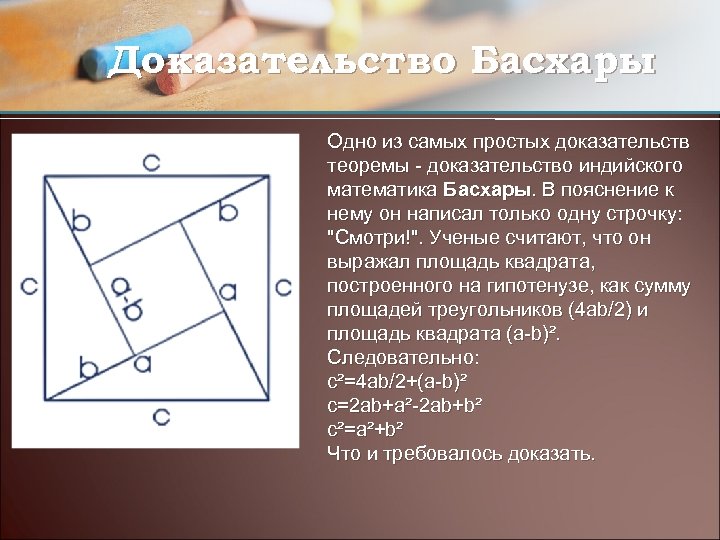
Доказательство Басхары Одно из самых простых доказательств теоремы - доказательство индийского математика Басхары. В пояснение к нему он написал только одну строчку: "Смотри!". Ученые считают, что он выражал площадь квадрата, построенного на гипотенузе, как сумму площадей треугольников (4 ab/2) и площадь квадрата (a-b)². Следовательно: c²=4 ab/2+(a-b)² c=2 ab+a²-2 ab+b² c²=a²+b² Что и требовалось доказать.

Алгебраическое доказательство Дано: ABC-прямоугольный треугольник Доказать: AB 2=AC 2+BC 2 Доказательство: 1) Проведем высоту CD из вершины прямого угла С. 2) По определению косинуса угла соs. А=AD/AC=AC/AB, отсюда следует AB*AD=AC 2. 3) Аналогично соs. В=BD/BC=BC/AB, значит AB*BD=BC 2. 4) Сложив полученные равенства почленно, получим: AC 2+BC 2=АВ*(AD + DB) AB 2=AC 2+BC 2.

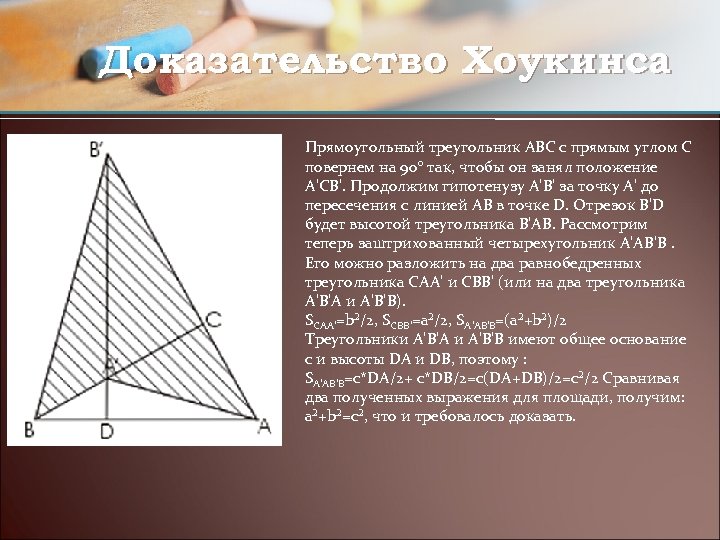
Доказательство Хоукинса Прямоугольный треугольник ABC с прямым углом C повернем на 90° так, чтобы он занял положение A'CB'. Продолжим гипотенузу A'В' за точку A' до пересечения с линией АВ в точке D. Отрезок В'D будет высотой треугольника В'АВ. Рассмотрим теперь заштрихованный четырехугольник A'АВ'В. Его можно разложить на два равнобедренных треугольника САA' и СВВ' (или на два треугольника A'В'А и A'В'В). SCAA'=b²/2, SCBB'=a²/2, SA'AB'B=(a²+b²)/2 Треугольники A'В'А и A'В'В имеют общее основание с и высоты DA и DB, поэтому : SA'AB'B=c*DA/2+ c*DB/2=c(DA+DB)/2=c²/2 Сравнивая два полученных выражения для площади, получим: a²+b²=c², что и требовалось доказать.

Доказательство через подобны треугольники Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. a/c=HB/a, b/c=AH/b т. е. a 2=c*HB , b 2=c*AH Следовательно a 2+b 2=c*(HB+AH)=c 2 Что и требовалось доказать.

Геометрическое доказательств Дано: ABC-прямоугольный треугольник Доказать: BC 2=AB 2+AC 2 Доказательство: 1) Построим отрезок CD равный отрезку AB на продолжении катета AC прямоугольного треугольника ABC. Затем опустим перпендикуляр ED к отрезку AD, равный отрезку AC, соединим точки B и E. 2) Площадь фигуры ABED можно найти, если рассматривать её как сумму площадей трёх треугольников: SABED=2*AB*AC/2+BC 2/2 3) Фигура ABED является трапецией, значит, её площадь равна: SABED= (DE+AB)*AD/2. 4) Если приравнять левые части найденных выражений, то получим: AB*AC+BC 2/2=(DE+AB)(CD+AC)/2 AB*AC+BC 2/2= (AC+AB)2/2 AB*AC+BC 2/2= AC 2/2+AB*AC BC 2=AB 2+AC 2. Это доказательство было опубликовано в 1882 году Гэрфилдом.

Доказательство через равнодополняемость

Доказательство Евклида Все доказательство теоремы сводится к доказательству равенства площадей квадрата ABFH и прямоугольника BDJL (или квадрата ACKG и прямоугольника CJLE). Треугольники ABD и BFC равны по двум сторонам и углу между ними: FB = AB, BC = BD, <FBC = <D + <ABC = <ABD. SABD = 1/2 S BJLD , SFBC=1/2 S ABFH Тогда SABD=SFBC, SBJLD=SABFH. Также доказывается и SJCEL=SACKG А затем SABFH+SACKG= SBJLD+SJCEL= SBCED т. е. a 2+b 2=c 2 , что и требовалось доказать.

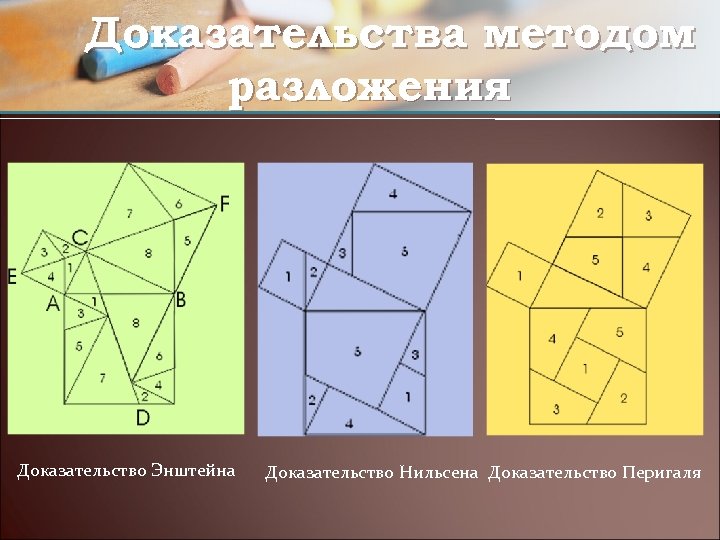
Доказательства методом разложения Доказательство Энштейна Доказательство Нильсена Доказательство Перигаля

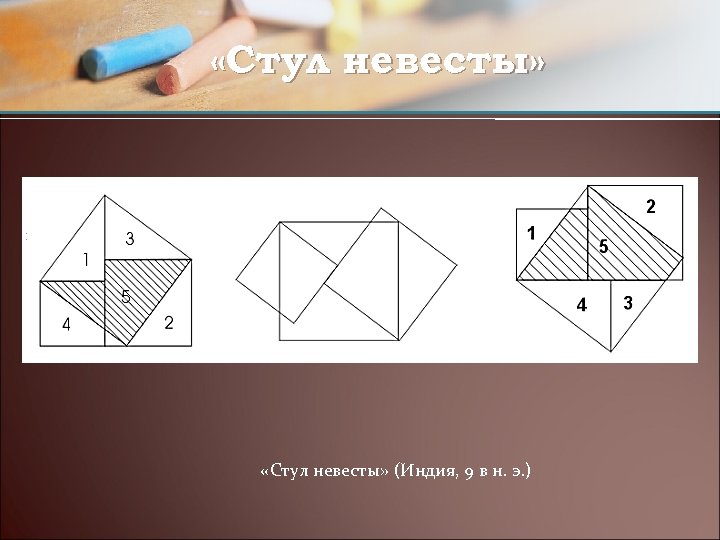
«Стул невесты» (Индия, 9 в н. э. )

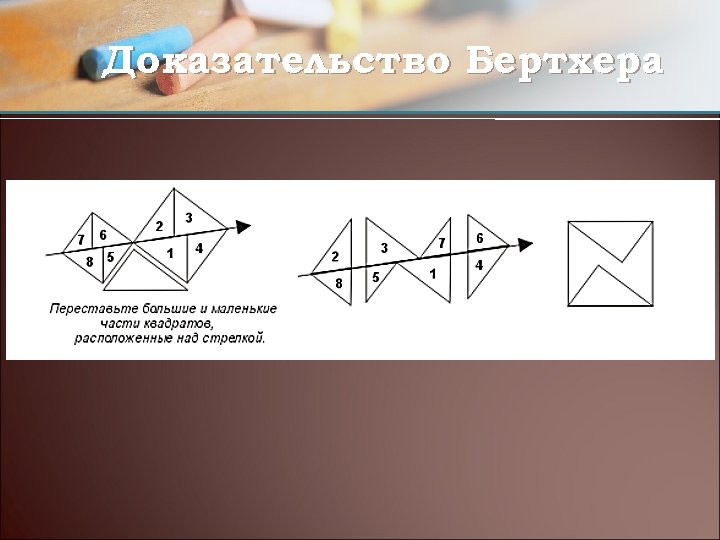
Доказательство Бертхера

Практическое применение Теорема Пифагора используется практически везде: в строительстве: для проектирования чертежа крыши дома, создания некоторых видов окон; в астрономии, в работе мобильной связи и в других вещах, которыми мы пользуемся ежедневно.

Значение теоремы Пифагора • Теорема Пифагора - это одна из самых важных теорем геометрии. Значение её состоит в том, что из неё или с её помощью можно вывести большинство теорем геометрии.

Заключение • В заключении хотелось бы отметит, что хотя теорема Пифагора и была известна около 4000 лет назад, люди ещё находят новые способы её доказательства. Так что может быть и вы откроете ещё одно. Надо только захотеть.

• Доказательство теоремы Пифагора учащиеся средних веков считали очень трудным и называли его Dons asinorum - ослиный мост, или elefuga - бегство «убогих» , так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Слабые ученики, заучившие теоремы наизусть, без понимания, и прозванные поэтому «ослами» , были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста. Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее также «ветряной мельницей» , составляли стихи, вроде «Пифагоровы штаны на все стороны равны» , рисовали карикатуры.

Литературные источники • 1)Энциклопедия для детей «Аванта» . Математика том 11. Москва 2004 • 2)wikipedia. ru • 3)pifagor. ru • 4)google. imagine. ru