Источники ЭМП Неподвижные заряды Дифференциальные характеристики неподвижных зарядов

Источники ЭМП Неподвижные заряды Дифференциальные характеристики неподвижных зарядов Объемная плотность зарядов (количество заряда в единице объема) , Кл/м³ поверхностная плотность зарядов (количество заряда на единице поверхности) , Кл/м² линейная плотность зарядов (количество заряда на единицу длины заряженной нити) , Кл/м Интегральные характеристики неподвижных зарядов количество заряда в объеме V, Кл количество заряда на поверхности S, Кл количество заряда на заряженной нити L, Кл

точечный заряд, Кл Движущиеся заряды Дифференциальная характеристика движущихся зарядов Вектор плотности тока проводимости (определяет скорость прохождения положительного заряда через единицу поверхности, ориентированную в направлении максимальной величины этой скорости), А/м² Интегральная характеристика движущихся зарядов Электрический ток проводимости, А

Структура ЭМП Векторы ЭМП Напряженность электрического поля , В/м (силовая характеристика электрического поля) Электрическая индукция (вектор электрического смещения) , Кл/м² Магнитная индукция магнитного поля , Тл (силовая характеристика магнитного поля) Напряженность магнитного поля , А/м

Уравнения ЭМП в интегральной форме Закон полного тока Закон электромагнитной индукции Постулат Максвелла Принцип непрерывности магнитного поля (условие соленоидальности магнитного поля) Материальные уравнения поля Для диэлектрической среды Для магнитных сред Для проводящих сред

- Абсолютная диэлектрическая проницаемость диэлектрика, ф/м - диэлектрическая постоянная - Абсолютная магнитная проницаемость магнетика, Гн/м - магнитная постоянная - Электрическая проводимость (электропроводность) проводящей среды, 1/Омм Уравнения ЭМП в дифференциалиной форме Закон полного тока Закон электромагнитной индукции

Постулат Максвелла Принцип непрерывности магнитного поля (условие соленоидальности магнитного поля) Энергия ЭМП Удельная энергия электрического поля, Дж/м³ Удельная энергия магнитного поля, Дж/м³ Энергия ЭМП в объеме V, Дж

Уравнения электростатического поля (поле неподвижных зарядов) Условие потенциальности электростатического поля Постулат Максвелла Условие потенциальности позволяет ввести скалярную функцию – электростатический потенциал В декартовой системе

Три векторных уравнения превращаются в одно скалярное для электростатического потенциала Для однородной среды ( ) получим или Уравнение Пуассона Для области , где нет зарядов Уравнение Лапласа В декартовой системе

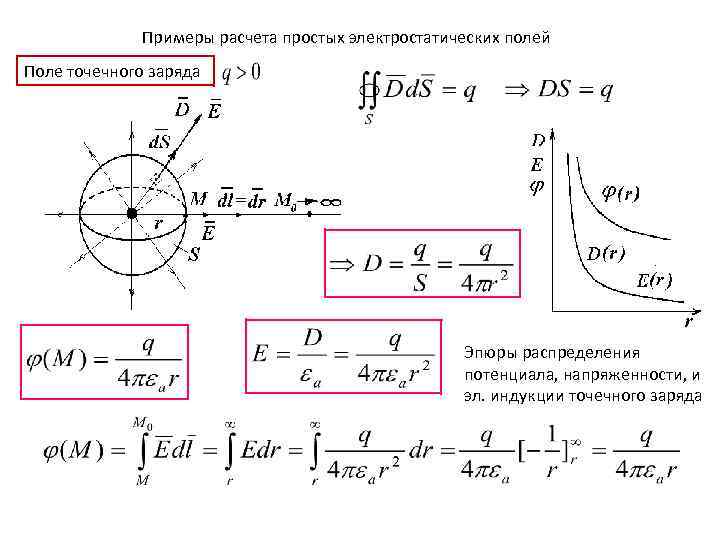Примеры расчета простых электростатических полей Поле точечного заряда Эпюры распределения потенциала, напряженности, и эл. индукции точечного заряда

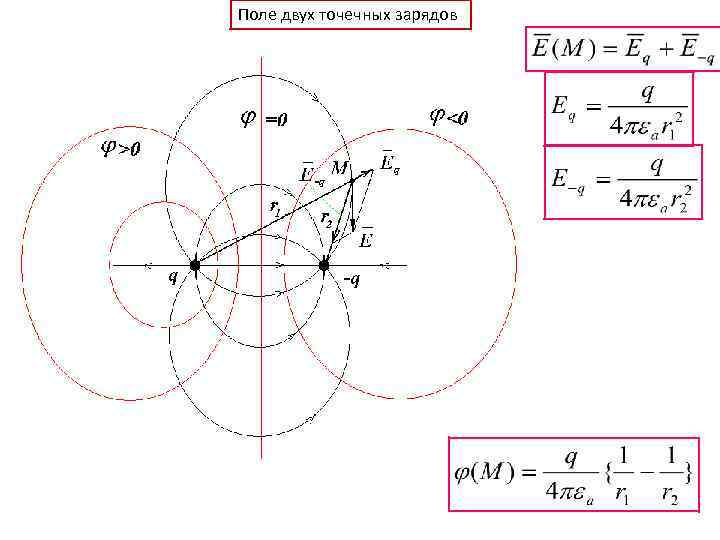Поле двух точечных зарядов

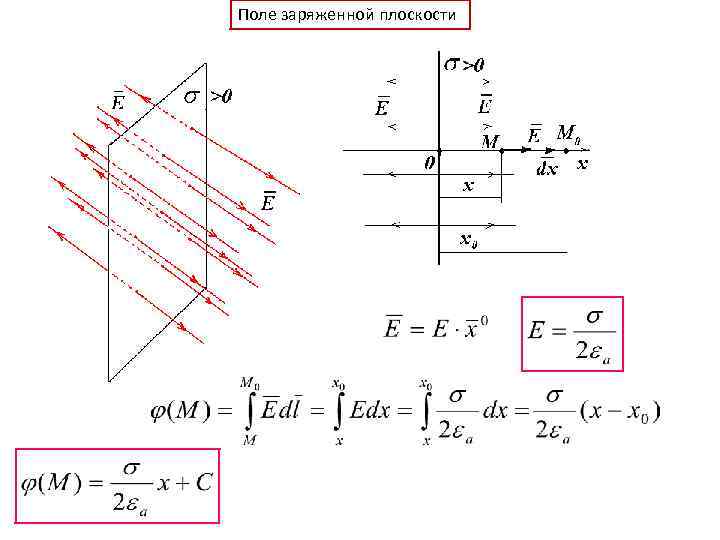Поле заряженной плоскости

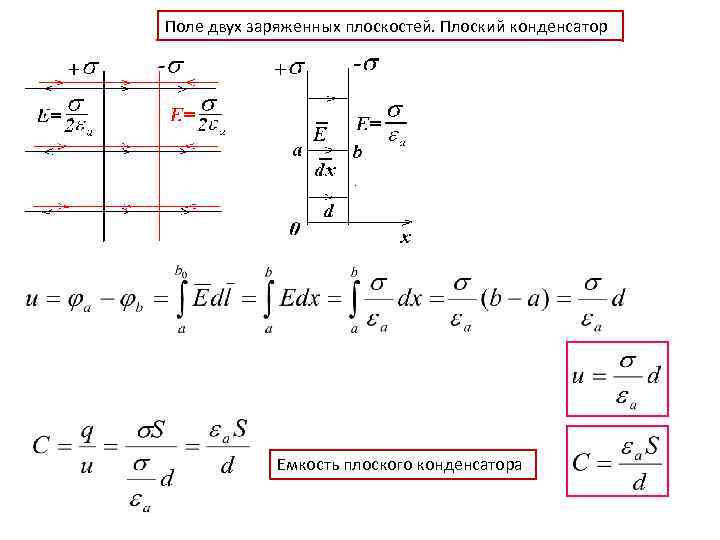Поле двух заряженных плоскостей. Плоский конденсатор Емкость плоского конденсатора

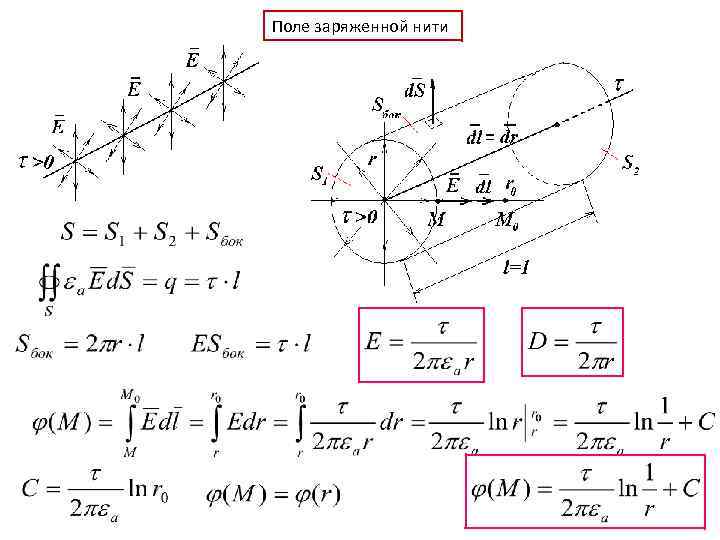Поле заряженной нити

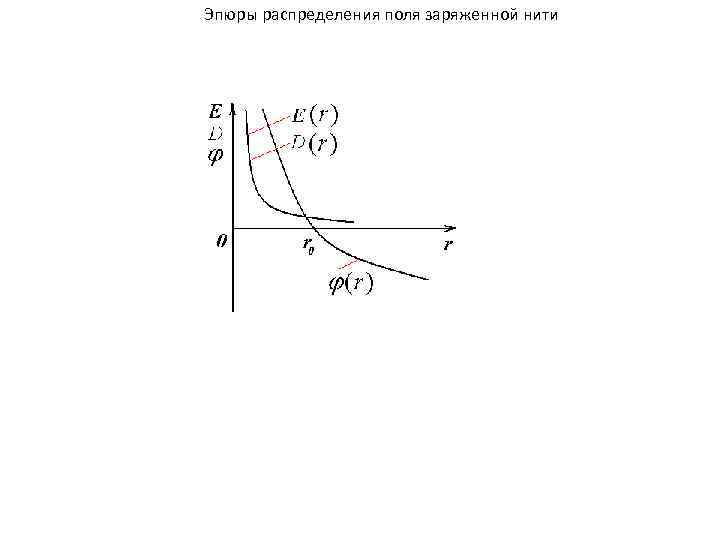Эпюры распределения поля заряженной нити

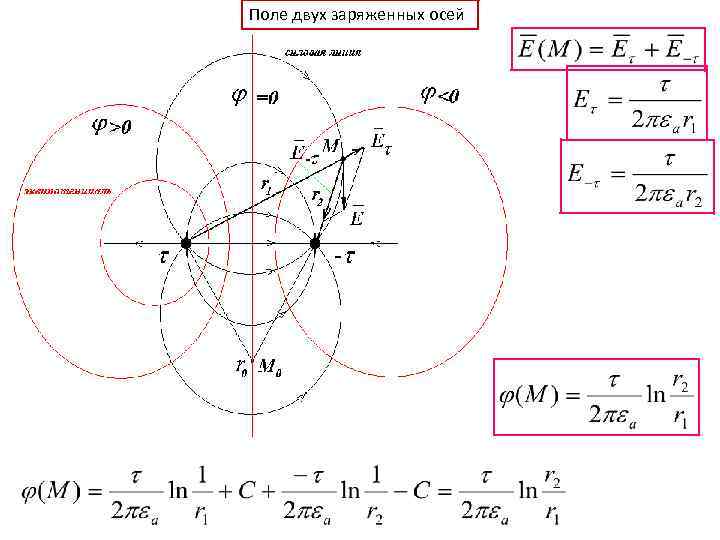Поле двух заряженных осей

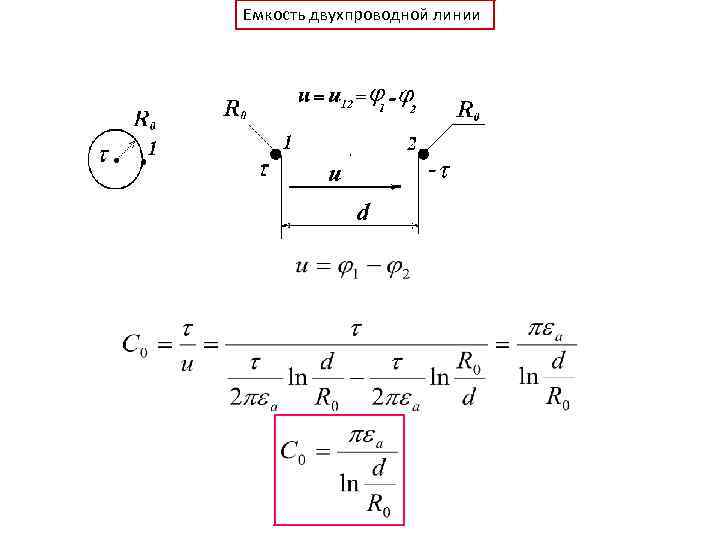Емкость двухпроводной линии

Объемный потенциал. Краевые задачи по методу наложения объемный потенциал Объемный потенциал справедлив для однородного пространства. Если область ограничена объемом V, то распределение потенциала ищется как решение краевой задачи если ρ=0, то краевая задача Дирихле

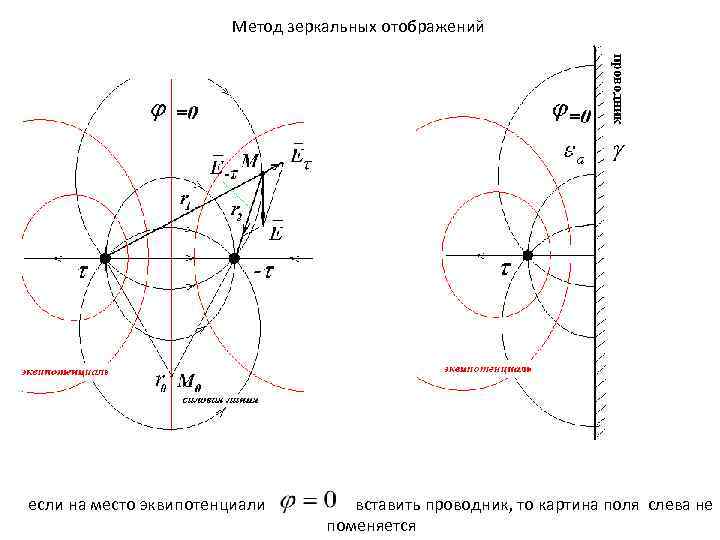Метод зеркальных отображений если на место эквипотенциали вставить проводник, то картина поля слева не поменяется

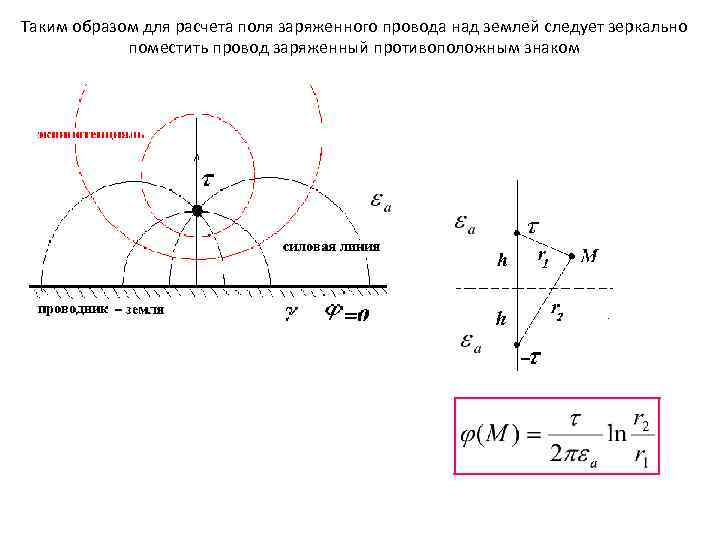Таким образом для расчета поля заряженного провода над землей следует зеркально поместить провод заряженный противоположным знаком

Связь потенциалов заряженных тел с их зарядами. Потенциальные коэффициенты, коэффициенты электростатической индукции, частичные емкости Потенциальные коэффициенты

Потенциальные коэффициенты системы заряженных тел определяются матрицей этих коэффициентов Потенциальные коэффициенты позволяют определять потенциалы тел , если заданы заряды тел При известных потенциалах решение системы позволяет определить заряды тел Коэффициенты называют коэффициентами электростатической индукции

частичные емкости определяют схему замещения системы проводников в электростатическом поле

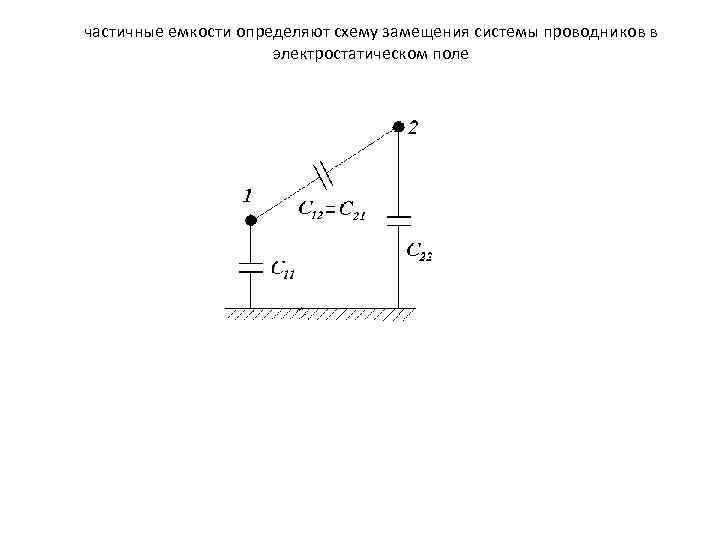частичные емкости определяют схему замещения системы проводников в электростатическом поле

Расчет электростатического поля двухпроводной заряженной линии в прямоугольном проводящем туннеле Дано: рассчитать: потенциал и напряженность электростатического поля в точке М Потенциал в точке М от заряженной линии при отсутствии проводящего туннеля Потенциал в точке М от индуцированных зарядов на поверхности проводящего туннеля Так как туннель проводник, то на его поверхности потенциал результирующего поля постоянен и его можно принять равным нулю

следовательно Потенциалы от заряженных осей (без учета индуцированных зарядов) Потенциал на контуре следа туннеля Потенциал в точке М

Для потенциала от индуцированных зарядов внутри туннеля будет справедливо уравнение Лапласа при заданном распределении этого потенциала на границе туннеля, то есть задача Дирихле Решением уравнения Лапласа являются функции , обладающие такими свойствами: -значение потенциала в точке М равно среднему от потенциалов точек окрестности. -потенциалы точек внутри области не могут быть больше максимального значения на границе области и меньше наименьшего граничного значения Эти свойства определяются : -теоремой о среднем -теоремой о максимуме и миниуме

теорема о среднем Свойства потенциала, полученные как решение уравнения Лапласа позволяют получать решение численным методом- методом сеток Для этого прямоугольную область (сечение туннеля) разбивают на ячейки (наносят сетку ). В узлах сетки должны быть определены значения потенциалов По теореме о среднем (по обозначениям рисунка)

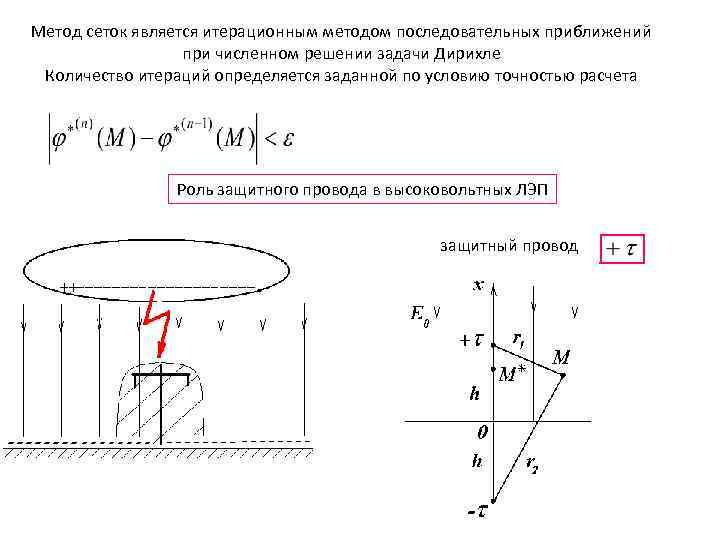Метод сеток является итерационным методом последовательных приближений при численном решении задачи Дирихле Количество итераций определяется заданной по условию точностью расчета Роль защитного провода в высоковольтных ЛЭП защитный провод

Потенциал поля , созданный зарядом грозового облака и зарядом на заземленном защитном проводе равен Потенциал поля , созданный зарядом грозового облака Потенциал поля , созданный зарядом на заземленном защитном проводе Если точку М поместить на поверхность земли (потенциал равен 0 ), то получим следовательно

Найдем проекцию вектора напряженности Е на ось Х напряженность Е на оси ОХ будет равна нулю при Х: При = 0. 01 м Х=0. 858 h Вблизи этой точки будет защитная зона

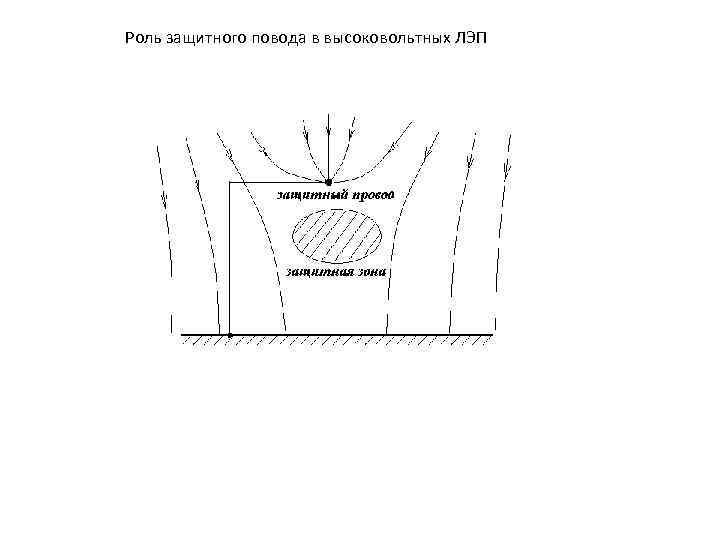Роль защитного повода в высоковольтных ЛЭП

Магнитное поле постоянного тока Так как магнитное поле вихревое , то для упрощения его описания вводят не скалярный, а векторный потенциал тогда при

Векторное уравнение Пуассона Расчеты простейших магнитных полей Магнитное поле бесконечно длиной линии с током - радиус провода

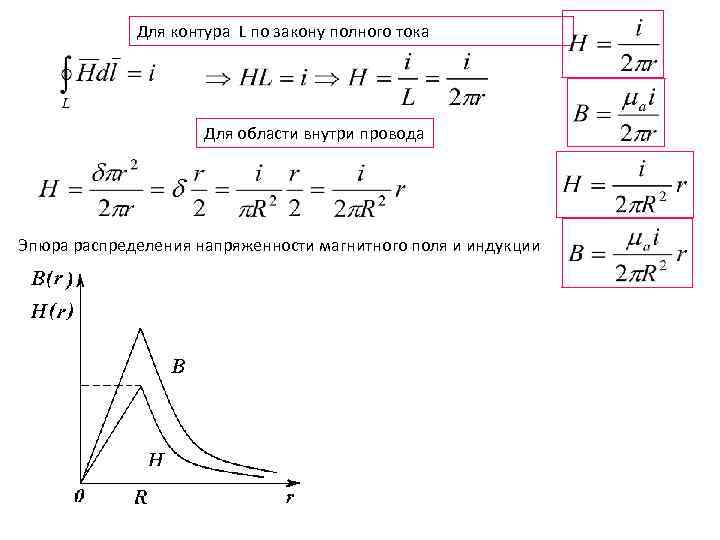Для контура L по закону полного тока Для области внутри провода Эпюра распределения напряженности магнитного поля и индукции

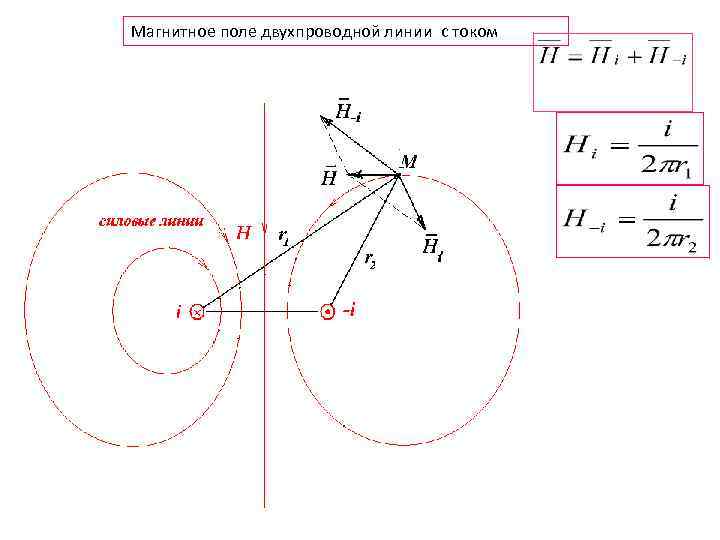Магнитное поле двухпроводной линии с током

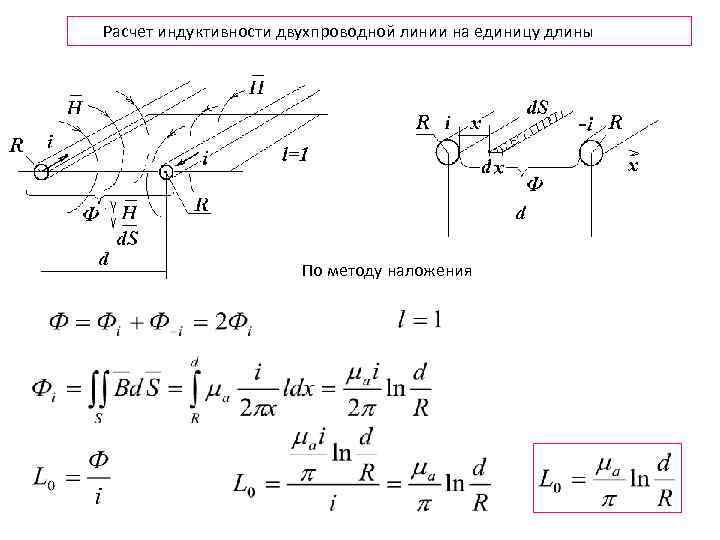Расчет индуктивности двухпроводной линии на единицу длины По методу наложения

Расчет взаимной индуктивности двухпроводной линии и рамки

вычисление магнитного потока с помощью векторного потенциала Интеграл по площади заменяется интегралом по контуру, охватывающему эту площадь (теорема Стокса) Для магнитного поля б/длинного проводника с током векторный потенциал имеет только одну проекцию по направлению провода и определяется по формуле Для двухпроводной линии с током

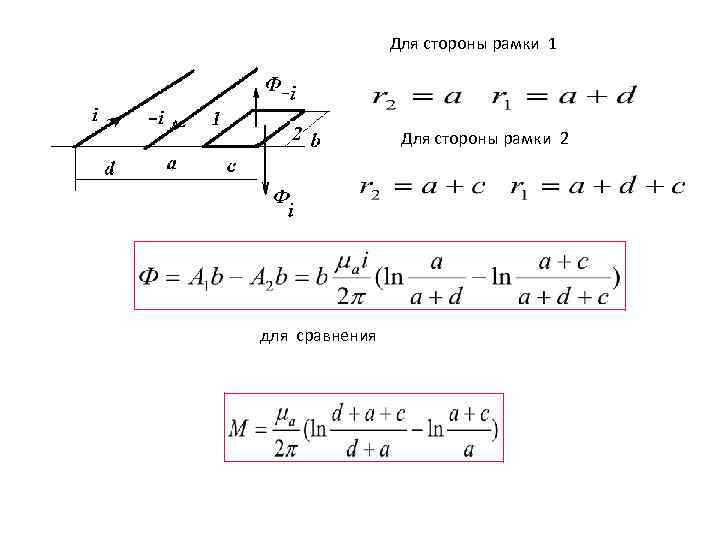Для стороны рамки 1 Для стороны рамки 2 для сравнения