ЛК_5_6_Gidrav_2012.pptx
- Количество слайдов: 47

ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ, НАСАДКОВ И КОРОТКИХ ТРУБ

• Задача об истечении жидкости через отверстия – одна из основных в гидравлике и решается она уже две тысячи лет, восходя к Герону Александрийскому. • Решение ее сводится к определению скорости истечения и расхода вытекающей жидкости. • Этот случай движения характеризуется тем, что в процессе истечения запас потенциальной энергии, которой обладает жидкость в резервуаре, превращается с большими или меньшими потерями в кинетическую энергию свободной струи или капель. • В зависимости от размеров и формы различают малые и большие отверстия в тонкой и толстой стенках.

классификация напорных систем 1. ТРУБОПРОВОДЫ (местные потери энергии пренебрежимо малы по сравнению с потерями по длине) 2. КОРОТКИЕ ТРУБЫ (местные потери соизмеримы с потерями по длине) 3. НАСАДКИ (местные потери значительно превосходят потери по длине) 4. ОТВЕРСТИЯ В ТОНКОЙ СТЕНКЕ (длина насадка не влияет на характер истечения)

ВИДЫ ОТВЕРСТИЙ 1. МАЛОЕ – наибольший вертикальный размер - d<0, 1 H (напора над отверстием) и скорость истечения постоянна по всему сечению 2. БОЛЬШОЕ – d>0, 1 H; скорость и давление в различных точках поперечного сечения струи отличаются, следовательно применять уравнение Бернулли нельзя
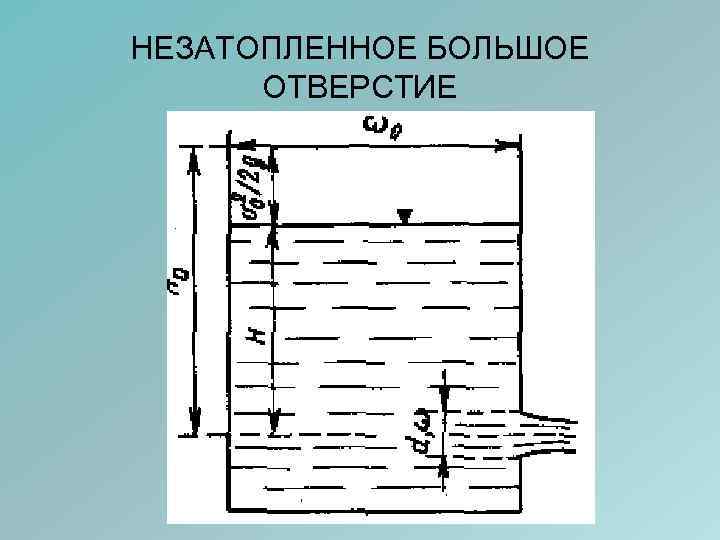
НЕЗАТОПЛЕННОЕ БОЛЬШОЕ ОТВЕРСТИЕ

ВИДЫ СТЕНОК 1. «ТОНКАЯ» стенка не влияет на характер истечения, если толщина стенок резервуара δ < 3 d (d – диаметр) 2. «ТОЛСТЫЕ» стенки, НАСАДКИ или КОРОТКИЕ ТРУБЫ влияют на характер истечения, так как струя соприкасается с отверстием только по внутренней кромке, далее отрывается от стенок по всей длине, если толщина стенок (длина трубы) δ>3÷ 4 d (L > 3÷ 4 d)
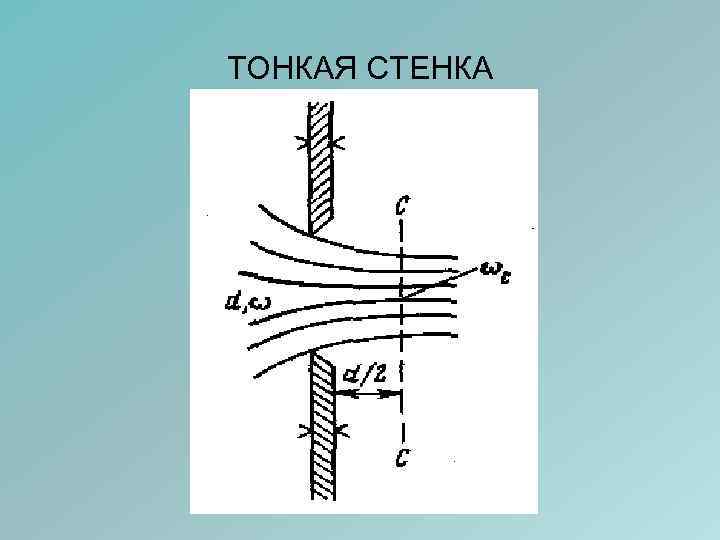
ТОНКАЯ СТЕНКА
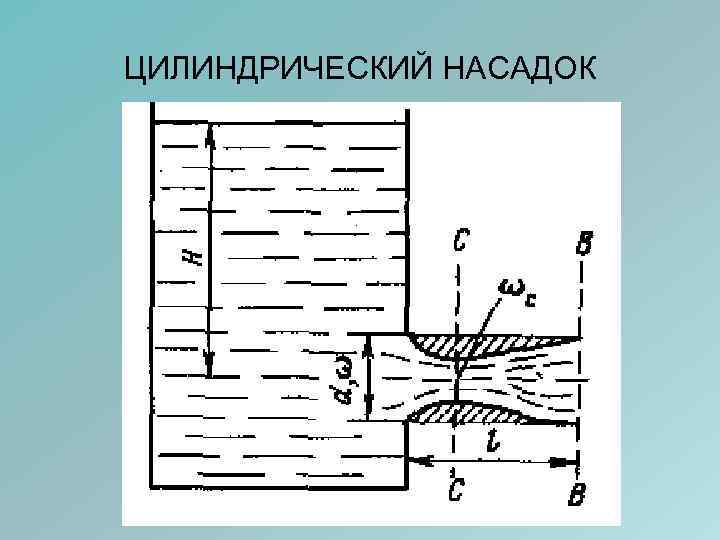
ЦИЛИНДРИЧЕСКИЙ НАСАДОК

В зависимости от расположения отверстия и условий протекания жидкости различают • полное и неполное сжатие струи, • совершенное и несовершенное сжатие струи, • истечение из затопленного и незатопленного отверстия • истечение при постоянном и переменном напоре.

РАЗЛИЧНЫЕ СЛУЧАИ СЖАТИЯ 1. ПОЛНОЕ сжатие – струя вытекающей жидкости, испытывает сжатие по всему периметру отверстия 2. НЕПОЛНОЕ сжатие – струя подвергается сжатию только на некоторой части периметра (если, например, отверстие располагается в углу или на дне)

РАЗЛИЧНЫЕ СЛУЧАИ СЖАТИЯ 1. СОВЕРШЕННОЕ сжатие – достигается максимальное сжатие струи (на рис. l 1>3 a, l 2>3 b) тогда, наблюдается когда боковые стенки и дно резервуара не влияют на истечение жидкости, т. е. удалены от отверстия на расстояние превышающее утроенный поперечный размер отверстия 2. НЕСОВЕРШЕННОЕ сжатие – достигается при более близком расположении отверстия к направляющим стенкам резервуара
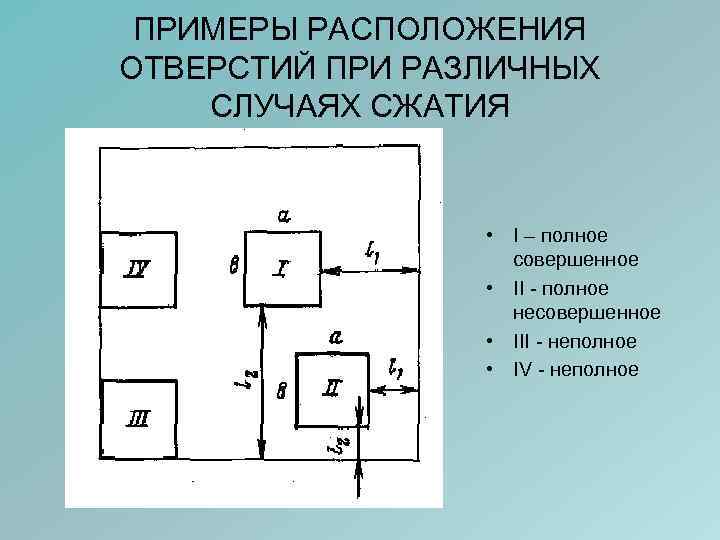
ПРИМЕРЫ РАСПОЛОЖЕНИЯ ОТВЕРСТИЙ ПРИ РАЗЛИЧНЫХ СЛУЧАЯХ СЖАТИЯ • I – полное совершенное • II - полное несовершенное • III - неполное • IV - неполное

Истечение из затопленного и незатопленного отверстия • Отверстие считается незатопленным, если истечение жидкости происходит в атмосферу. • Отверстие считается затопленным, если истечение происходит не в атмосферу, а под уровень жидкости.
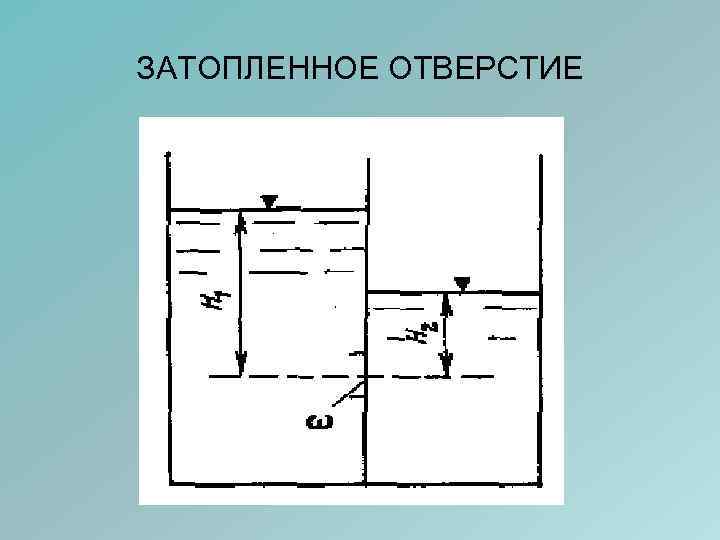
ЗАТОПЛЕННОЕ ОТВЕРСТИЕ

Истечение жидкости при постоянном и переменном напоре • • При постоянном уровне – установившееся движение жидкости При переменном уровне – неустановившееся движение жидкости

Формулы для расчета скорости и расхода при истечении жидкости из малых незатопленных отверстий в тонкой стенке при постоянном напоре

истечение жидкости из малого круглого отверстия • Возьмем большой резервуар с жидкостью под давлением Pат, имеющий малое круглое отверстие в стенке на достаточно большой глубине Н от свободной поверхности • Частицы жидкости приближаются к отверстию из всего прилежащего объема, двигаясь ускоренно по различным плавным траекториям. • Струя отрывается от стенки у кромки отверстия и затем несколько сжимается. • Цилиндрическую форму струя принимает на расстоянии, равном примерно одному диаметру отверстия. • Сжатие струи обусловлено необходимостью плавного перехода от различных направлений движения жидкости в резервуаре, в том числе от радиально движения по стенке, к осевому движению в струе
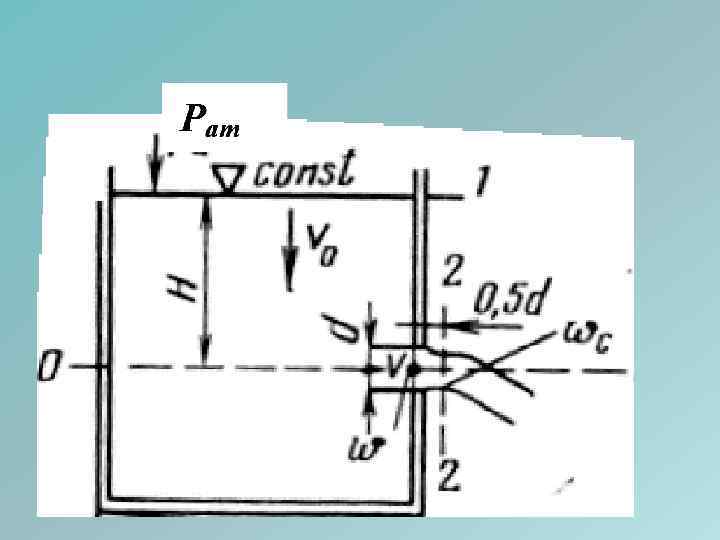

• Так как размер отверстия предполагается малым, по сравнению с напором Н и размерами резервуара и свободная поверхность жидкости не влияют на приток струи жидкости к отверстию, то наблюдается совершенное сжатие струи. • Степень сжатия оценивается коэффициентом сжатия ε, равным отношению площади поперечного сечения струи в месте сжатия к площади отверстия: ε = wс/w.

• Для определения скорости истечения и расхода жидкости составим уравнение Бернулли для сечений 1– 1 и 2– 2 относительно плоскости сравнения 0– 0, проходящей через центр отверстия H+pa /γ+ v 02/2 g= pa /γ + v 2/2 g+hw • Потери напора в данном случае представляют собой местные потери на входе в отверстие, т. е. : hw = hм=ζм v 2/2 g, здесь ζм – коэффициент сопротивления отверстия

скорость истечения жидкости: v=φ где φ – коэффициент скорости (для отверстия в тонкой стенке φ = 0, 97) коэффициент скорости φ есть отношение действительной скорости к теоретической: φ = v/vт теоретическая скорость истечения по формуле Торричелли равна vт =

• Расход жидкости в сжатом сечении можно определить из уравнения неразрывности: Q=wсж v • Практически удобнее пользоваться вместо wсж произведением εw • (где ε коэффициент сжатия для малых отверстий, равный 0, 6– 0, 64), таким образом, можно записать: Q= εw φ

• Произведение ε на φ принято обозначать буквой μ и называть коэффициентом расхода, подставив μ=εφ получим формулу для расчета расхода жидкости при истечении ее в атмосферу через отверстия и насадки Q= μ w

• На основе опытов установлено, что для малого отверстия в тонкой стенке μ колеблется от 0, 59 до 0, 63, или в среднем μ =0, 61. • Это выражение применимо для всех случаев истечения, трудность заключается в достаточной оценке коэффициента расхода μ • коэффициент расхода представляет собой отношение действительного расхода к теоретическому, который имел бы место при отсутствии сжатия струи и сопротивления • Действительный расход всегда меньше теоретического, следовательно, коэффициент μ всегда меньше 1 вследствие влияния двух факторов: сжатия струи и сопротивления

• Введенные коэффициенты – сопротивления отверстия ζ, коэффициент расхода μ и коэффициент скорости φ зависят в первую очередь от типа отверстия и насадка, а также как и все безразмерные коэффициенты в гидравлике, от основного критерия гидродинамического подобия – числа Re.
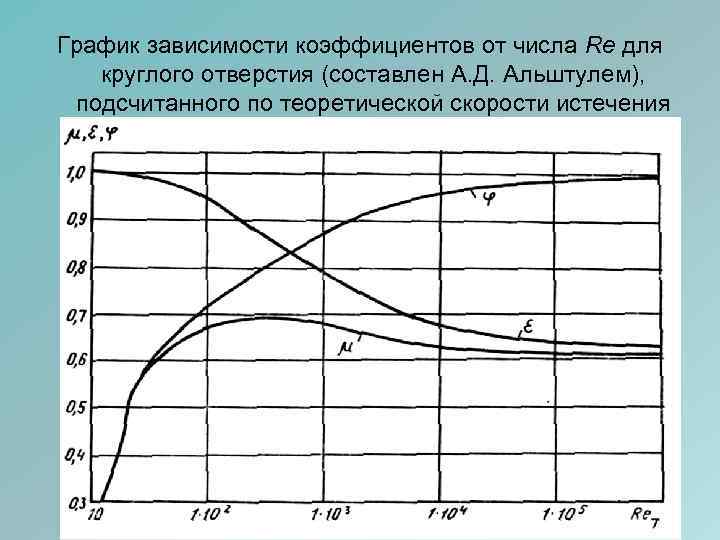
График зависимости коэффициентов от числа Re для круглого отверстия (составлен А. Д. Альштулем), подсчитанного по теоретической скорости истечения

• При истечении воды и других жидкостей малой вязкости из отверстий малого диаметра (d<3 см) и при малых напорах коэффициенты истечения ε, φ, μ могут испытывать заметное влияние поверхностного натяжения. • С увеличением поверхностного натяжения при истечении из малых отверстий в тонкой стенке уменьшается коэффициент скорости φ, возрастает коэффициент сжатия струи ε и уменьшается коэффициент расхода μ.

Коэффициенты расхода μ, скорости φ и сжатия ε зависят от: • Формы и кромки отверстия • Положения отверстия относительно стенок резервуара • Режима движения жидкости • Поверхностного натяжения жидкости Они рассчитаны для большинства случаев и сведены в таблицы или номограммы

Истечение жидкости при несовершенном сжатии • Несовершенное сжатие струи наблюдается в том случае, когда на истечение жидкости через отверстие и на формирование струи оказывает влияние близость боковых стенок резервуара. • Ввиду того, что боковые стенки частично направляют движение жидкости при подходе к отверстию, струя по выходе из отверстия сжимается в меньшей степени, чем при истечении из резервуара неограниченных размеров, когда имелось совершенное сжатие. • Вследствие уменьшения сжатия струи возрастет коэффициент сжатия струи, а следовательно и коэффициент расхода.

• Если направляющие стенки не совпадают ни с одной из кромок отверстия, то наблюдается полное сжатие. В противном случае наблюдается неполное сжатие, для которого: μнеп. сж= μ(1+Кn*), где μ – коэффициент расхода при полном сжатии, К – эмпирический коэффициент, n*= , א/*א - *א та часть периметра, по которой сжатие устранено направляющей стенкой, - א полный периметр отверстия

эмпирический коэффициент К имеет следующие значения: • • для круга – 0, 128, малого квадрата – 0, 152, малого прямоугольника – 0, 134, прямоугольника шириной 0, 2 и высотой 0, 16 – 0, 157. • Павловский Н. Н. рекомендует независимо от формы отверстий принимать К=0, 49

Истечение жидкости через затопленное отверстие • В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении. • Для затопленного отверстия формулы для определения скорости и расхода имеют тот же вид, что и для незатопленного отверстия. • Разница заключается в том, что под величиной Н подразумевается в случае затопленного отверстия не глубина погружения, а разность уровней в резервуарах: Q=μз w

Истечение жидкости через затопленное отверстие • Коэффициент сжатия струи ε и коэффициент сопротивления ζ при истечении при затопленном отверстии практически не отличается от соответствующих коэффициентов при истечении через незатопленное отверстие. • Опыт показывает, что коэффициент расхода μз при истечении через затопленное отверстие можно принимать равным коэффициенту μ для незатопленного отверстия
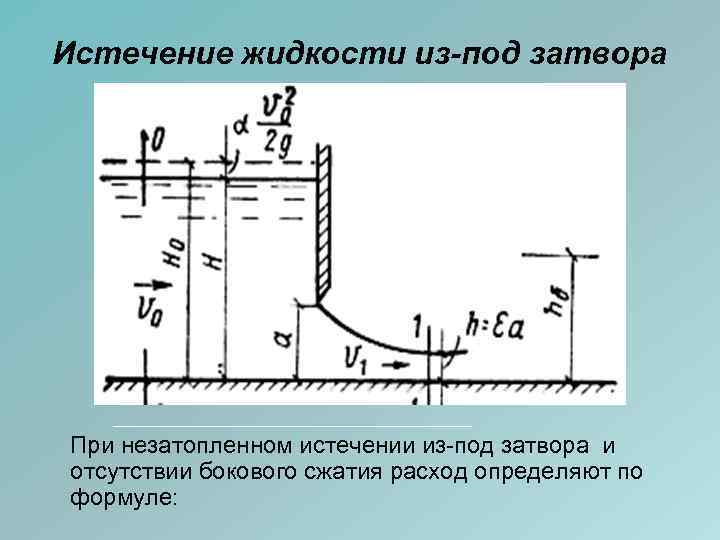
Истечение жидкости из-под затвора При незатопленном истечении из-под затвора и отсутствии бокового сжатия расход определяют по формуле:

Истечение жидкости из-под затвора где H – глубина воды перед отверстием; а – высота отверстия; b – ширина отверстия; φ – поправочный коэффициент, учитывающий влияние потерь напора, значение которого можно принимать по таблице, в зависимости от числа Фруда. j 1, 04 Fr=v 02/2 g. H 0, 002 0, 005 1, 02 0, 99 0, 975 0, 97 0, 965 0, 96 0, 01 0, 02 0, 03 0, 04 >0, 06

Истечение жидкости через большие отверстия Для отверстий любой формы: Q= μ w 0 где Н 0 – полный напор с учетом скорости подхода H 0 = H + v 02/2 g v 0 - средняя скорость потока выше отверстия
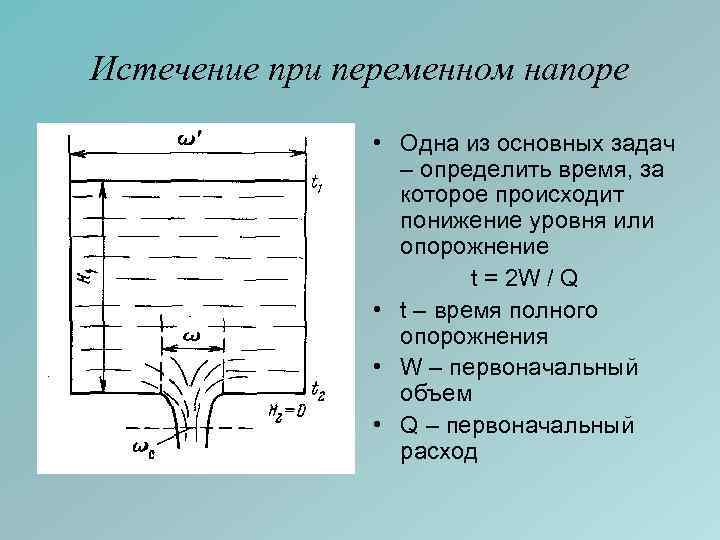
Истечение при переменном напоре • Одна из основных задач – определить время, за которое происходит понижение уровня или опорожнение t = 2 W / Q • t – время полного опорожнения • W – первоначальный объем • Q – первоначальный расход

Истечение жидкости через насадки и короткие трубы

Гидравлический насадок • Гидравлический насадок, это короткая труба для выпуска жидкости в атмосферу или перетекания жидкости из одного резервуара в другой, тоже заполненный жидкостью. • Насадками являются не только трубы, но и каналы, отверстия в толстых стенках, а также зазоры между деталями машин. • Длина насадка, при которой возможно заполнение всего сечения канала и достигается максимальная пропускная способность для внешних и внутренних цилиндрических насадков, составляет l =(3– 4) d.

• Насадки бывают трех типов: цилиндрические внешние и внутренние, конически сходящиеся и расходящиеся, коноидальные. • Все насадки, как и отверстия, могут работать в затопленном и незатопленном режиме, истечение жидкости через них может быть как при постоянном напоре, так и при переменном.

Типы насадков: а) цилиндрические внешние, б) внутренние, в) конически сходящиеся и г) расходящиеся, д) коноидальные

Насадки применяются в технике для различных целей • Для выпуска жидкости из резервуара и водоемов применяют различные цилиндрические насадки. Внешние и внутренние цилиндрические насадки увеличивают расход по сравнению просто с отверстием. • Для получения больших выходных скоростей и дальности полета струи жидкости применяют конически сходящиеся насадки в виде пожарных брандспойтов, форсунок для подачи топлива, гидромониторов, для размыва грунта, фонтанных сопел, сопел гидравлических турбин.

Насадки применяются в технике для различных целей • Наоборот, для замедления течения жидкости и увеличения давления во всасывающих трубах гидравлических турбин, для замедления подачи смазочных масел применяют конически расходящиеся насадки. Для конических сходящихся и расходящихся насадков существуют оптимальные углы конусности. • Наибольшей пропускной способностью обладает коноидальный насадок, продольное сечение которого выполняется по форме вытекающей из отверстия струи. • Насадки специальных конструкций применяют в форсунках для распыления топлива.

• В коноидальных насадках вход выполняют по форме вытекающей через отверстия струи, а выход – цилиндрическим, благодаря этому обеспечивает безотрывность течения внутри насадка параллейноструйность в выходном сечении. • За счет такой формы сжатие струи отсутствует, ε =1 и коэффициенты φ=μ. • Это весьма распространенный насадок, так как он имеет коэффициент расхода близкий к единице, и очень малые потери (ε =1), а также устойчивый режим истечения без кавитации. Значения коэффициента сопротивления те же, что и в случае плавного сужения, т. е. ζ=0, 03 -0, 10 (большим числам Re соответствуют меньшие ζ), φ = μ = 0, 99 -0, 96.

Формула для расчета расхода насадка: Q= μ нw где μ н – коэффициент расхода, отнесенный к выходному отверстию насадка w - площадь выходного отверстия насадка Н – напор над центром выходного отверстия насадка (или разность напоров при затопленном насадке)

Истечение жидкости из коротких труб • Короткие трубы рассчитывают так же, как цилиндрические насадки, но коэффициенты μ и φ должны учитывать и потери напора по длине. • Коэффициенты расхода и скорости в этом случае называют коэффициентами системы. • Как и для цилиндрического насадка, сжатие струи на выходе отсутствует, а поэтому μс = φс. Потери напора определяются как сумма потерь напора по длине и местных потерь

• Коэффициенты расхода для незатопленных труб • для затопленных • где R = d/4 - гидравлический радиус. Коэффициенты гидравлического трения λ вычисляются либо по графику Никурадзе, либо по соответствующим формулам
ЛК_5_6_Gidrav_2012.pptx