Исследовательская и проектная деятельность на уроках физики

Исследовательская и проектная деятельность на уроках физики

«Исследование – процесс поиска неизвестного, новых знаний, один из видов познавательной деятельности человека…» «Проектирование – это творчество по плану в определенных контролируемых рамках»

n n n Умение придумывать Умение прогнозировать Умение проводить исследование физических явлений Умение планировать учебную деятельность Умение выполнять рефлексию своей деятельности

Исследовательская работа «Экстремумы в задачах по физике»

Актуальность работы в том, что решение задач на экстремум имеет не только теоретический интерес. К решению данных задач сводятся иногда задачи связанные с практикой и повседневной деятельностью человека. Цель исследования: провести реферативноисследовательский анализ теоретических основ решения экстремальных задач на конкретных задачах. Продемонстрировать различные методы их решения. Экспериментально выявить факторы, влияющие на нахождение экстремальных величин.

• “Экстремум” в переводе с латинского означает “крайнее”. • Экстремальные задачи – это задачи на отыскание максимума или минимума.

В мире не происходит ничего, в чём бы не был виден смысл какого -нибудь максимума или минимума Леонард Эйлер

История изучения задач на экстремумы Герон Александрийский ( I век до н. э. ) -задача о кратчайшем пути луча Пьер Ферма ( XVII век) -закон преломления света Якоб Бернулли ( XVII век) -задача о брахистохроне или кривой наискорейшего спуска Иоганн Кеплер -задача о винных бочках

В разные времена этой проблемой занимались: Архимед Луи Бройль Жозеф Луи Готфрид Вильгельм Лагранж фон Лейбниц Рене Декарт Евклид Пьер Мопертюи Никколо Тарталья Макс Планк

Методы решения задач на экстремумы Теория оптимального управления Теория дифференциальног о исчисления Теория вариационного исчисления

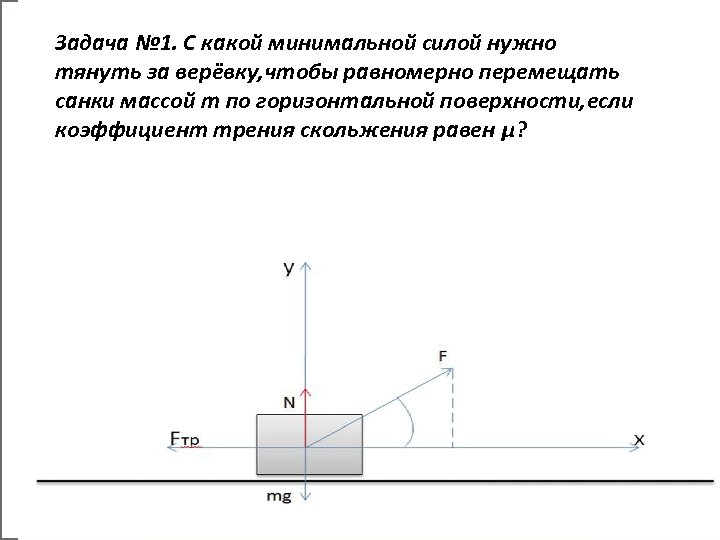Задача № 1. С какой минимальной силой нужно тянуть за верёвку, чтобы равномерно перемещать санки массой m по горизонтальной поверхности, если коэффициент трения скольжения равен μ?

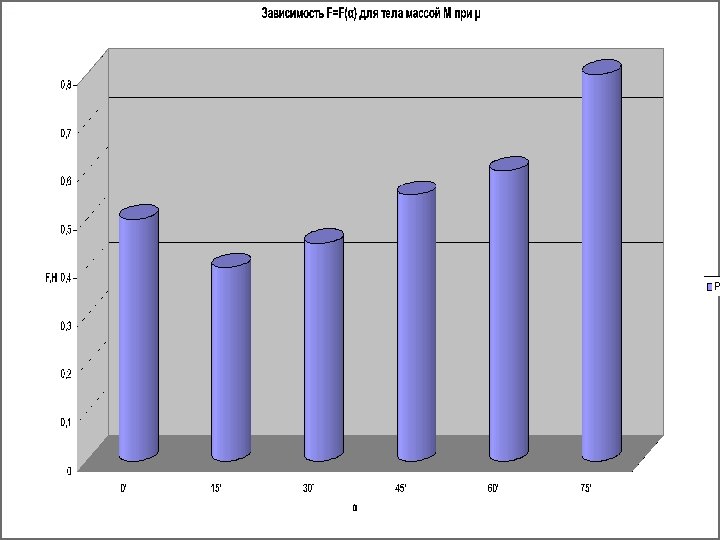
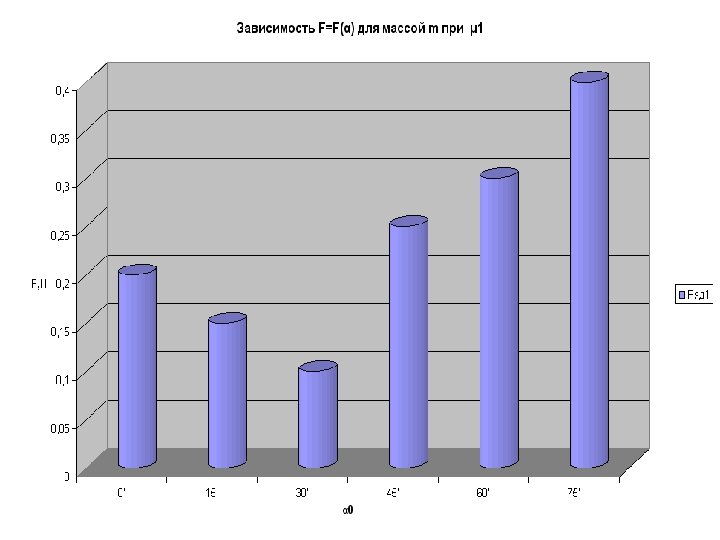
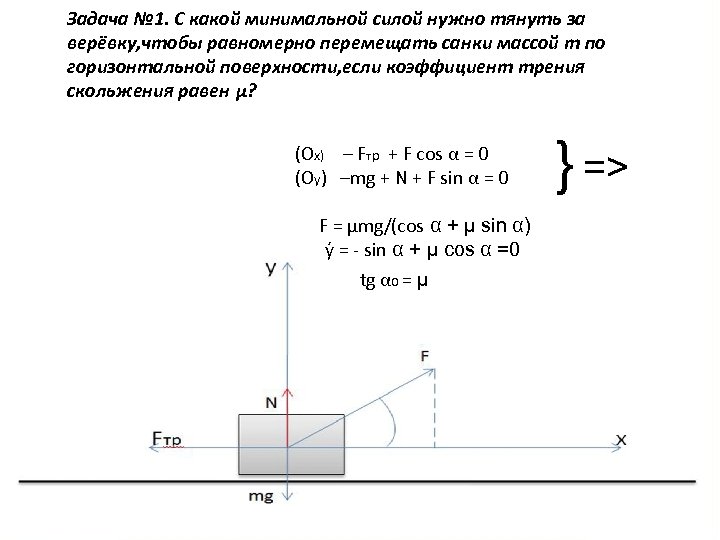Задача № 1. С какой минимальной силой нужно тянуть за верёвку, чтобы равномерно перемещать санки массой m по горизонтальной поверхности, если коэффициент трения скольжения равен μ? (Ox) – Fтр + F cos α = 0 (Oy) –mg + N + F sin α = 0 F = μmg/(cos α + μ sin α) y = - sin α + μ cos α =0 tg α 0 = μ } =>

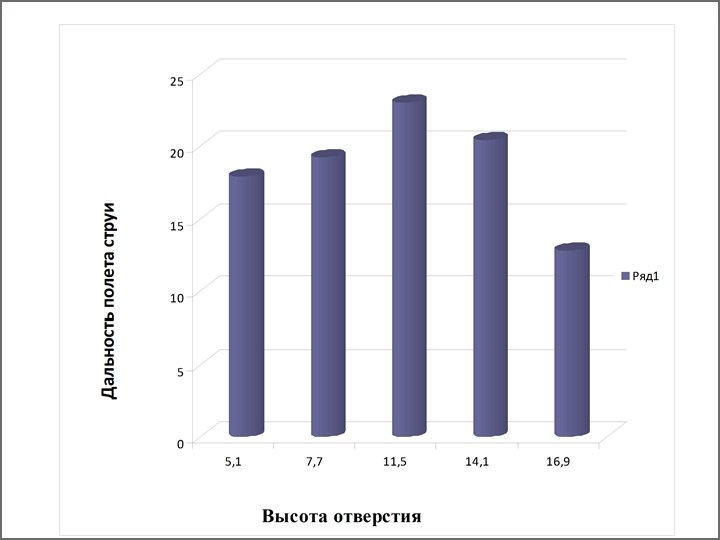
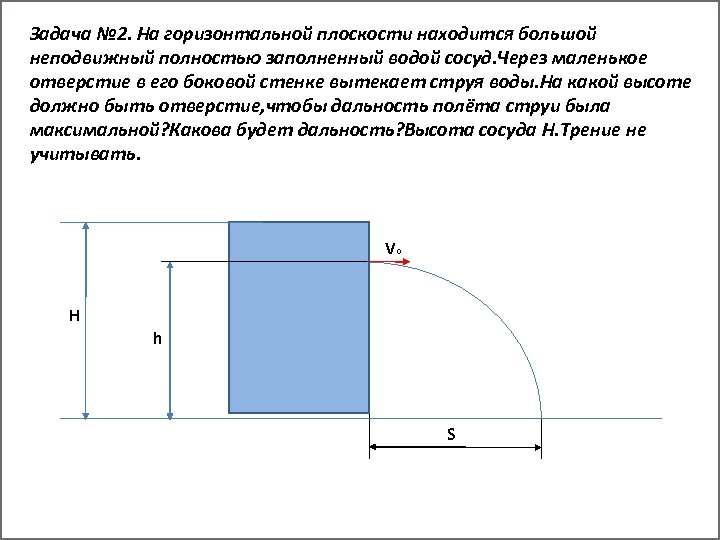Задача № 2. На горизонтальной плоскости находится большой неподвижный полностью заполненный водой сосуд. Через маленькое отверстие в его боковой стенке вытекает струя воды. На какой высоте должно быть отверстие, чтобы дальность полёта струи была максимальной? Какова будет дальность? Высота сосуда H. Трение не учитывать. Vo H h S

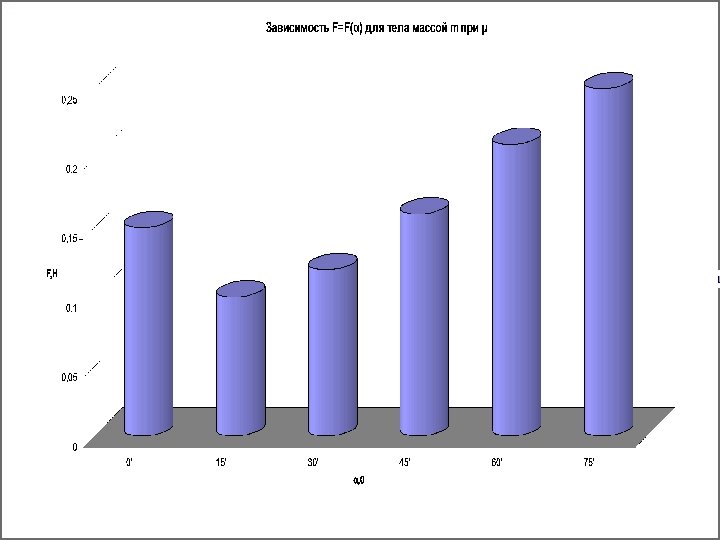
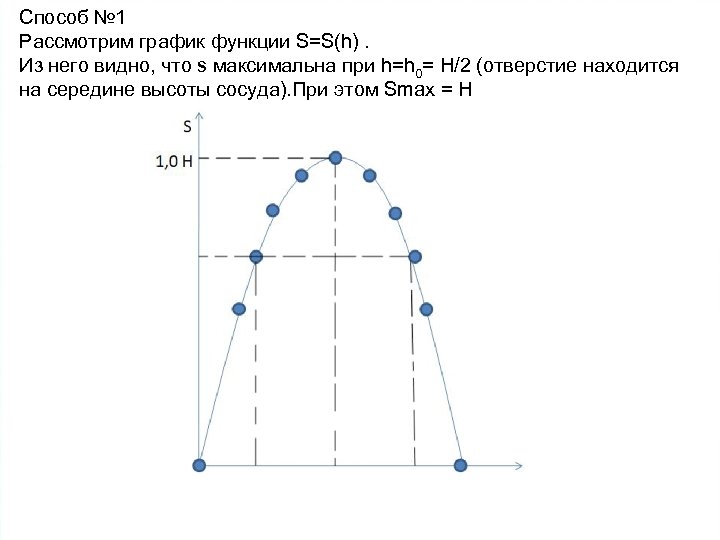Способ № 1 Рассмотрим график функции S=S(h). Из него видно, что s максимальна при h=h 0= H/2 (отверстие находится на середине высоты сосуда). При этом Smax = H

Способ» № 2 Эти же результаты можно получить аналитически. Действительно, функция S(h) максимальна, когда максимально подкоренное выражение. Обозначим его буквой y, возьмём y по аргументу h и приравняем её к нулю: y = H-2 h = 0. Отсюда h=h 0 =H/2 а, максимальная дальность Smax =H

Способ№ 3 Будем считать, что в уравнении задано S , а h - не известна. Переписав его в виде квадратного уравнения h 2 - Hh + S 2/4=0, Запишем условие равенства нулю дискриминанта: H 2 - S 2 max=0, Откуда получаем ответ: Smax=H.

Неньютоновские жидкости

Цель: n Изучение свойств неньютоновской жидкости

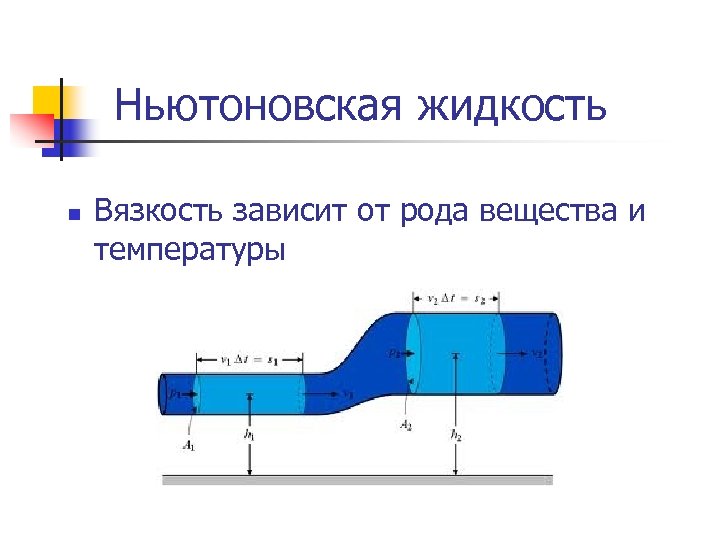Ньютоновская жидкость n Вязкость зависит от рода вещества и температуры

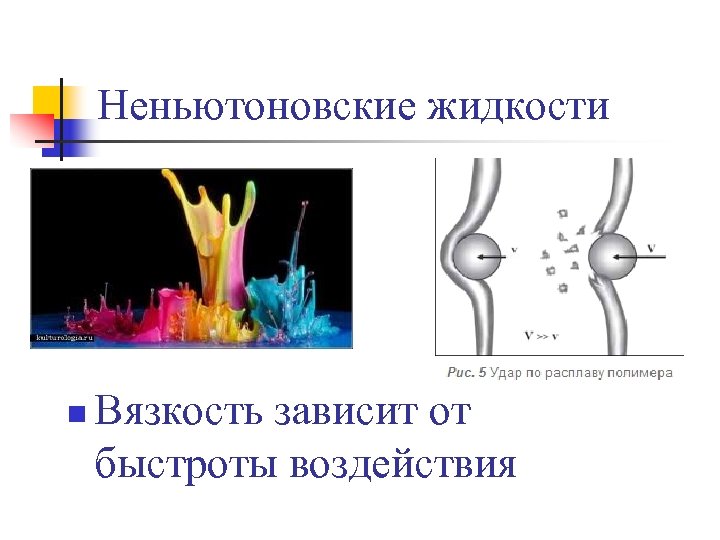Неньютоновские жидкости n Вязкость зависит от быстроты воздействия

Ход работы:

Что наблюдаем?

Применение неньютоновских жидкостей «Умный» пластилин

Бронежилет

Моторное масло

Неньютоновская жидкость починит дорожные ямы

Зыбучие пески