ef46060dcf7389c8c43362d11d950209.ppt
- Количество слайдов: 18

Исследование регламентируемых фрагментов российского Веба Печников Андрей Анатольевич, к. ф. -м. н. , ст. н. с. Институт прикладных математических исследований Карельского научного центра РАН

• Регламентируемый веб-ресурс - это веб-ресурс, для которого существует (должен существовать) нормативный документ, в котором изложены цели, задачи, основные структурные составляющие, правила обновления, добавления и изменения информации веб-ресурса. • Целевое множество - задаваемое прямым перечислением множество регламентируемых сайтов. • Сопутствующее множество - множество сайтов, не входящих в целевое множество, на которые существуют гиперссылки с сайтов целевого множества. • Фрагмент Веба - объединение сайтов целевого и сопутствующего множеств и множество связывающих их гиперссылок. 2

Объекты исследований: • академический фрагмент Веба (целевое множество – официальные сайты научных учреждений РАН); • университетский фрагмент Веба (целевое множество – официальные сайты классических университетов РФ); • бюрократический фрагмент Веба (целевое множество – официальные сайты органов государственной власти Республики Карелия). 3

Информационная система для вебометрических исследований: 1. Робот-сборщик гиперссылок 2. База данных Операции, функции, фильтры БД ВИ: Разработаны около 20 штук по мере возникновения необходимости. Первая – ВЫБОРКА, . . затем – ССЫЛКИ НА ЗАДАННЫЙ САЙТ, ССЫЛКИ С ЗАДАННОГО САЙТА, СОПУТСТВУЮЩЕЕ МНОЖЕСТВО, . . МАТРИЦА СМЕЖНОСТИ, . . . И т. д. 4
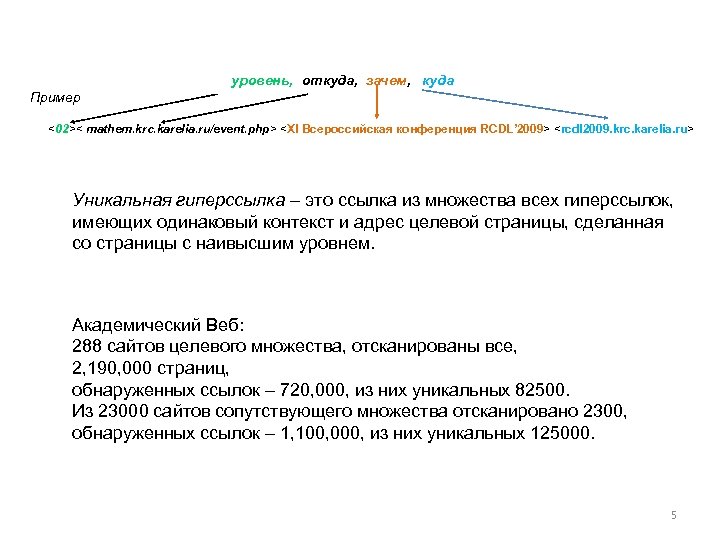
уровень, откуда, зачем, куда Пример <02>< mathem. krc. karelia. ru/event. php> <XI Всероссийская конференция RCDL’ 2009> <rcdl 2009. krc. karelia. ru> Уникальная гиперссылка – это ссылка из множества всех гиперссылок, имеющих одинаковый контекст и адрес целевой страницы, сделанная со страницы с наивысшим уровнем. Академический Веб: 288 сайтов целевого множества, отсканированы все, 2, 190, 000 страниц, обнаруженных ссылок – 720, 000, из них уникальных 82500. Из 23000 сайтов сопутствующего множества отсканировано 2300, обнаруженных ссылок – 1, 100, 000, из них уникальных 125000. 5
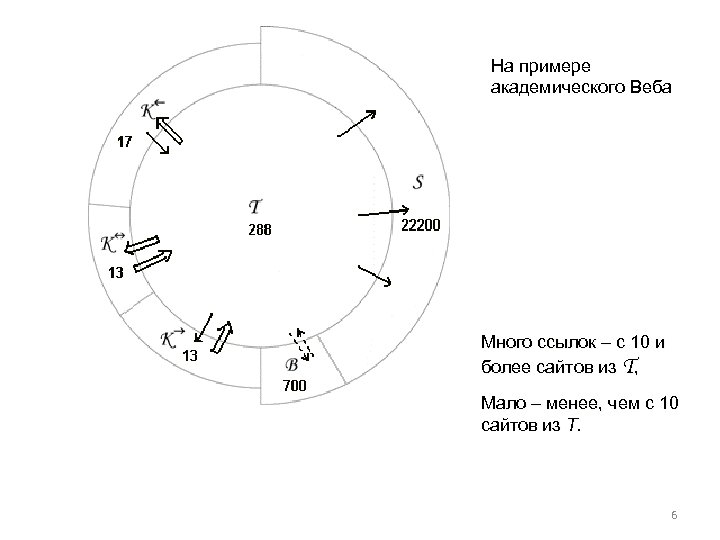
На примере академического Веба Много ссылок – с 10 и более сайтов из T, Мало – менее, чем с 10 сайтов из T. 6
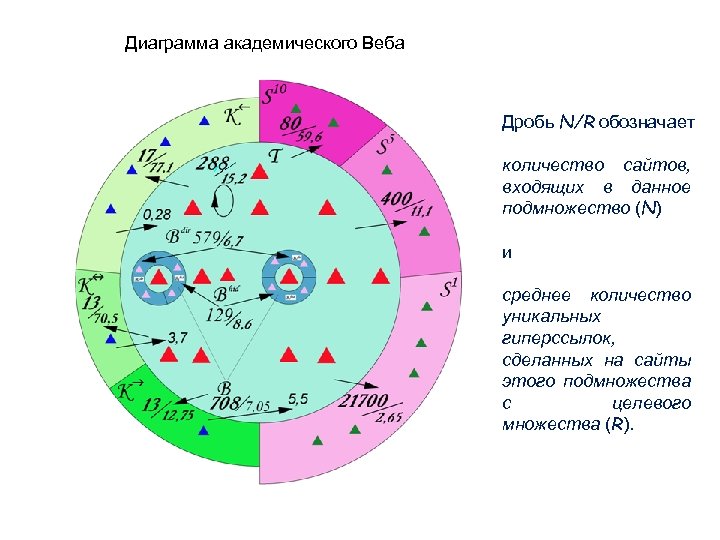
Диаграмма академического Веба Дробь N/R обозначает количество сайтов, входящих в данное подмножество (N) и среднее количество уникальных гиперссылок, сделанных на сайты этого подмножества с целевого множества (R).
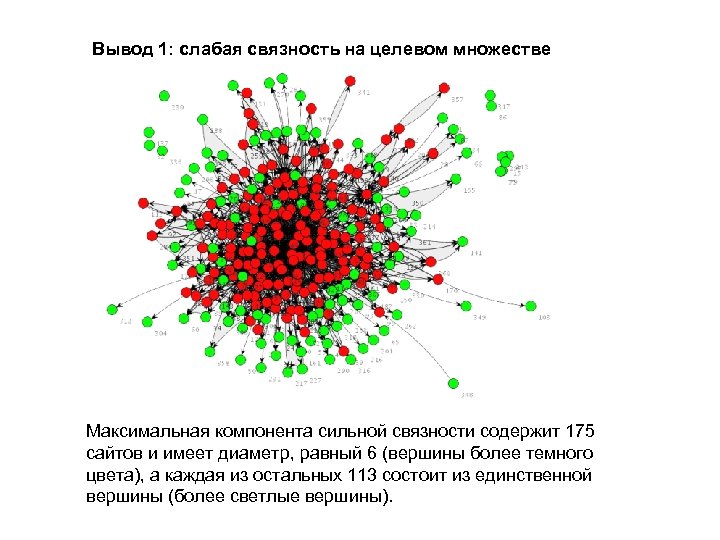
Вывод 1: слабая связность на целевом множестве Максимальная компонента сильной связности содержит 175 сайтов и имеет диаметр, равный 6 (вершины более темного цвета), а каждая из остальных 113 состоит из единственной вершины (более светлые вершины).

Примеры: Сайты-коммуникаторы академического Веба 1 2 3 4 5 6 Академические коллекторы (17) РФФИ Научная электронная библиотека ВАК Московский государственный университет МАИК Наука_Интерпериодика Роснаука РФ 102 62 44 33 53 26 9 1 3 4 2 3 1 2 3 4 5 Академические посредники (8) Новосибирский государственный университет Отделение ГПНТБ СО РАН Междисциплинарный научный сервер Московский физико-технический институт Библиотека по естественным наукам РАН Новосибирский государственный технический 6 университет 1 2 3 4 5 6 Академические индукторы (8) Все о геологии Общероссийский математический портал Портал для аспирантов Библиотека Академии Наук Исторический факультет МГУ Издательство СО РАН Прикладные проблемы управления макросистемами 2010 8 8 7 6 6 6 27 23 23 22 19 10 14 118 13 37 16 10 24 13 17 20 19 20 9

Вывод 2 : ценность коммуникаторов • При добавлении коллекторов: мощность максимальной компоненты связности увеличивается до 214. • При добавлении индукторов: мощность максимальной компоненты связности увеличивается до 190. • При добавлении посредников: мощность максимальной компоненты связности увеличивается до 191. • При добавлении всех трех подмножеств коммуникаторов: мощность максимальной компоненты связности увеличивается до 237. • Во всех четырех случаях диаметр наибольшей компоненты связности становится равным 7.

Пример взвешенного веб-графа для 4 сайтов. Граф – сильно связный. Дуги имеют различные веса. d(i, t) – длина кратчайшего пути из вершины i в вершину t в графе G(T, Е), где i, t T. Критерий доступности сайта t на множестве T - средняя длина пути в заданную вершину t T из любой вершины i T, i≠t, которая задается следующим образом: На примере для вершины 1: midd(1)=(1+3+1)/3=5/3. Далее будем использовать просто сумму, а не среднюю сумму, т. к. это не влияет на результат. Задача дележа затрат (1) 11
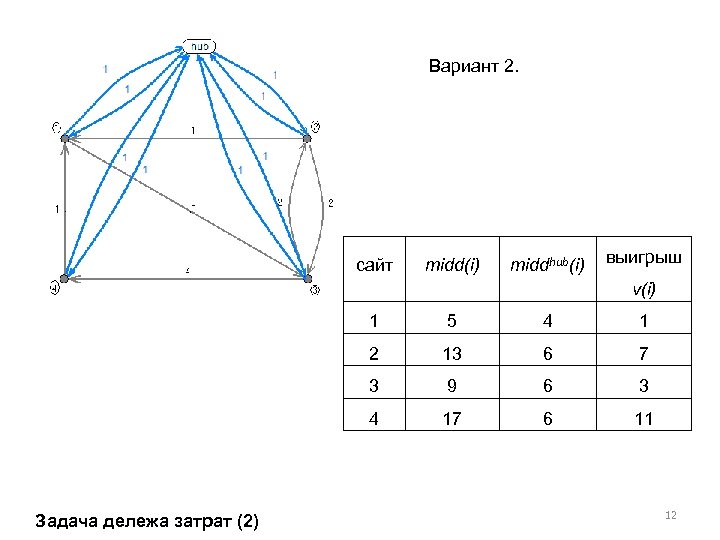
Вариант 2. сайт midd(i) middhub(i) выигрыш v(i) 1 4 1 2 13 6 7 3 9 6 3 4 Задача дележа затрат (2) 5 17 6 11 12

Вариант 3. Кооперативные игры. Вектор Шепли — принцип оптимальности распределения выигрыша между игроками в задачах теории кооперативных игр. Представляет собой распределение, в котором выигрыш каждого игрока равен его среднему вкладу в благосостояние тотальной коалиции при определенном механизме ее формирования. Задача дележа затрат (3) 13

На нашем примере сайт midd(i) выигрыш w(i) 1 5 4, 67 0, 33 2 13 5, 83 7, 17 3 9 2, 67 6, 33 4 17 8, 83 8, 17 выигрыш Вар 2 v(i) 1 4, 55% 7 31, 82% 3 13, 64% 11 50, 00% Задача дележа затрат (4) выигрыш w(i) 0, 33 7, 17 6, 33 8, 17 Вар 3 1, 50% 32, 59% 28, 77% 37, 14% 14

Пусть n – количество участников, ci – значимость i-го участника, ci>0, i=1. . n, mi – максимально возможное количество прямых ссылок от i-го на других участников, mi>0, i=1. . n. Матрица ссылок X=(xij), i, j=1. . n, где xij=1, если существует ссылка от i-го участника к j-му, и xij=0, если нет. Ограничения будут определены несколько ниже. F(X) ‑ функция, характеризующая некоторый интегральный показатель значимости всех участников веб-системы и зависящая от того, каким образом расставлены ссылки между ее участниками. Функция приращения значимости: – чем больше ссылок на ресурс, тем он становится «значимее» , – чем больше значимость ресурса i, тем больше возрастает значимость ресурса j, если xij=1, – чем больше исходящих ссылок от ресурса i, тем меньше приращение значимости каждого ресурса j, для которого xij=1. Задача расстановки ссылок в локализованной системе веб-ресурсов (1)

• Ограничения • Целевая функция 1 Чем меньше , тем больше • Целевая функция 2 Задача расстановки ссылок в локализованной системе веб-ресурсов (2)

, Задача расстановки ссылок в локализованной системе веб-ресурсов (3) Апробация и модификация моделей на данных Яндекса ограничение в качестве заменено на строгое равенство, приняты значения т. ИЦ, отобрано 20 реальных сообществ, содержащих от 7 до 84 участников. • • • По модели 1: Религия. Православие, Баннерная сеть Ket. Ru, Министерства РФ, Сайты Кар. НЦ РАН (0. 905), Целлюлозно-Бумажная Баннерная Сеть По модели 2: Сайты Кар. НЦ РАН, Министерства РФ, Баннерная сеть Ket. Ru, Религия. Православие, Целлюлозно-Бумажная Баннерная Сеть. Задача расстановки ссылок в локализованной системе веб-ресурсов (3)

18
ef46060dcf7389c8c43362d11d950209.ppt