8907f84a800dbc71a8db98b305e0a402.ppt
- Количество слайдов: 180
 Исследование операций в экономике Составлено к. т. н. профессором С. Н. Мартышенко
Исследование операций в экономике Составлено к. т. н. профессором С. Н. Мартышенко
 Лекция 1 Тема: Введение в исследование операций Рассматриваются вопросы: 1. Литература 2. Исследование операций, как научная дисциплина, история развития дисциплины. 3. Основные понятия исследования операций: операция, математическая модель операции, оптимальное решение, эффективность операции. 4. Классификация основных типов моделей исследования операций.
Лекция 1 Тема: Введение в исследование операций Рассматриваются вопросы: 1. Литература 2. Исследование операций, как научная дисциплина, история развития дисциплины. 3. Основные понятия исследования операций: операция, математическая модель операции, оптимальное решение, эффективность операции. 4. Классификация основных типов моделей исследования операций.
 3. Основные понятия исследования операций: операция, математическая модель операции, оптимальное решение, эффективность операции. Операция – любое управляемое мероприятие, направленное на достижение цели. Результат операции зависит от способа ее проведения, организации, иначе – от выбора некоторых параметров. Модель операции это достаточное описание операции с помощью математического аппарата (различного рода функций, уравнений, систем уравнений и неравенств и т. п. ). Оптимальными считаются те решения, которые по тем или иным соображениям предпочтительнее других. Эффективность операции – степень ее приспособленности к выполнению задачи – количественно выражается в виде критерия эффективности – целевой функции.
3. Основные понятия исследования операций: операция, математическая модель операции, оптимальное решение, эффективность операции. Операция – любое управляемое мероприятие, направленное на достижение цели. Результат операции зависит от способа ее проведения, организации, иначе – от выбора некоторых параметров. Модель операции это достаточное описание операции с помощью математического аппарата (различного рода функций, уравнений, систем уравнений и неравенств и т. п. ). Оптимальными считаются те решения, которые по тем или иным соображениям предпочтительнее других. Эффективность операции – степень ее приспособленности к выполнению задачи – количественно выражается в виде критерия эффективности – целевой функции.
 1. Литература
1. Литература
 2. Исследование операций, как научная дисциплина, история развития дисциплины (слайд 1). Исследование операций – научная дисциплина, занимающаяся разработкой и практическим применением методов наиболее эффективного управления различными организационными системами. Целью исследования операций является количественное обоснование принимаемых решений по организации управления.
2. Исследование операций, как научная дисциплина, история развития дисциплины (слайд 1). Исследование операций – научная дисциплина, занимающаяся разработкой и практическим применением методов наиболее эффективного управления различными организационными системами. Целью исследования операций является количественное обоснование принимаемых решений по организации управления.
 2. Исследование операций, как научная дисциплина, история развития дисциплины (слайд 2). Применение методов исследования операций предполагает : 1. Построение экономических и математических моделей для задач принятия решения в сложных ситуациях или в условиях неопределенности; 2. Изучение взаимосвязей, определяющих в последствии принятие решений, и установление критериев эффективности, позволяющих оценивать преимущество того или иного варианта действия.
2. Исследование операций, как научная дисциплина, история развития дисциплины (слайд 2). Применение методов исследования операций предполагает : 1. Построение экономических и математических моделей для задач принятия решения в сложных ситуациях или в условиях неопределенности; 2. Изучение взаимосвязей, определяющих в последствии принятие решений, и установление критериев эффективности, позволяющих оценивать преимущество того или иного варианта действия.
 3. Основные понятия исследования операций: операция, математическая модель операции, оптимальное решение, эффективность операции. Операция – любое управляемое мероприятие, направленное на достижение цели. Результат операции зависит от способа ее проведения, организации, иначе – от выбора некоторых параметров. Модель операции это достаточное описание операции с помощью математического аппарата (различного рода функций, уравнений, систем уравнений и неравенств и т. п. ). Оптимальными считаются те решения, которые по тем или иным соображениям предпочтительнее других. Эффективность операции – степень ее приспособленности к выполнению задачи – количественно выражается в виде критерия эффективности – целевой функции.
3. Основные понятия исследования операций: операция, математическая модель операции, оптимальное решение, эффективность операции. Операция – любое управляемое мероприятие, направленное на достижение цели. Результат операции зависит от способа ее проведения, организации, иначе – от выбора некоторых параметров. Модель операции это достаточное описание операции с помощью математического аппарата (различного рода функций, уравнений, систем уравнений и неравенств и т. п. ). Оптимальными считаются те решения, которые по тем или иным соображениям предпочтительнее других. Эффективность операции – степень ее приспособленности к выполнению задачи – количественно выражается в виде критерия эффективности – целевой функции.
 4. Классификация основных типов моделей исследования операций. По содержательной постановке различают ряд типов задач исследования операций: 1. 2. 3. 4. 5. 6. 7. 8. 9. Задача сетевого планирования и управления. Задача массового обслуживания. Задача управления запасами. Задача распределения ресурсов. Задача ремонта и замены оборудования. Задача составления расписаний. Задача планировки и размещения. Задача выбора маршрута. Задачи теории игр.
4. Классификация основных типов моделей исследования операций. По содержательной постановке различают ряд типов задач исследования операций: 1. 2. 3. 4. 5. 6. 7. 8. 9. Задача сетевого планирования и управления. Задача массового обслуживания. Задача управления запасами. Задача распределения ресурсов. Задача ремонта и замены оборудования. Задача составления расписаний. Задача планировки и размещения. Задача выбора маршрута. Задачи теории игр.
 Лекция 2 Тема: Основы линейного программирования. Графическое решение задачи линейного программирования. Рассматриваются вопросы: 1. Примеры задач линейного программирования. 1. 1. Задача составления рациона. 1. 2. Задача использования ресурсов. 1. 3. Основные этапы записи модели линейного программирования. 2. Стандартная и каноническая формы записи модели линейного программирования. 3. Основные приемы перехода от произвольной записи модели к стандартной и канонической форме записи.
Лекция 2 Тема: Основы линейного программирования. Графическое решение задачи линейного программирования. Рассматриваются вопросы: 1. Примеры задач линейного программирования. 1. 1. Задача составления рациона. 1. 2. Задача использования ресурсов. 1. 3. Основные этапы записи модели линейного программирования. 2. Стандартная и каноническая формы записи модели линейного программирования. 3. Основные приемы перехода от произвольной записи модели к стандартной и канонической форме записи.
 1. Примеры задач линейного программирования. 1. 1. Задача составления рациона (слайд 1). Исходные данные задачи Поголовье 20000 цыплят Средний расход корма на единицу на период планирования – 0, 5 кг Таблица 1. Требования по питательности Вид корма Содержание питательных веществ кг/кг корма Стоимость руб. /кг кальций белок клетчатка Известняк 0. 380 4 Зерно 0. 001 0. 09 0. 02 15 Соевые бобы 0. 002 0. 50 0. 08 40
1. Примеры задач линейного программирования. 1. 1. Задача составления рациона (слайд 1). Исходные данные задачи Поголовье 20000 цыплят Средний расход корма на единицу на период планирования – 0, 5 кг Таблица 1. Требования по питательности Вид корма Содержание питательных веществ кг/кг корма Стоимость руб. /кг кальций белок клетчатка Известняк 0. 380 4 Зерно 0. 001 0. 09 0. 02 15 Соевые бобы 0. 002 0. 50 0. 08 40
 1. Примеры задач линейного программирования. 1. 1. Задача составления рациона (слайд 2). Требования к кормовой смеси по питательности - смесь должна содержать: 1) не менее 0. 8%, но не более 1. 2% кальция; 2) не менее 22% белка; 3) не более 5% клетчатки. Цель Птицеводческой ферме необходимо составить рацион минимальной стоимости при соблюдении требований по питательности.
1. Примеры задач линейного программирования. 1. 1. Задача составления рациона (слайд 2). Требования к кормовой смеси по питательности - смесь должна содержать: 1) не менее 0. 8%, но не более 1. 2% кальция; 2) не менее 22% белка; 3) не более 5% клетчатки. Цель Птицеводческой ферме необходимо составить рацион минимальной стоимости при соблюдении требований по питательности.
 1. Примеры задач линейного программирования. 1. 1. Задача составления рациона (слайд 3). Процесс построения математической модели можно представить как ответы на следующие три вопроса: 1. Для определения каких величин должна быть построена модель? 2. В чем состоит цель, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать оптимальному (наилучшему) решению задачи? 1. 3. Какие ограничения должны быть наложены на переменные, чтобы выполнить условия, отраженные в содержательной постановке задачи?
1. Примеры задач линейного программирования. 1. 1. Задача составления рациона (слайд 3). Процесс построения математической модели можно представить как ответы на следующие три вопроса: 1. Для определения каких величин должна быть построена модель? 2. В чем состоит цель, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать оптимальному (наилучшему) решению задачи? 1. 3. Какие ограничения должны быть наложены на переменные, чтобы выполнить условия, отраженные в содержательной постановке задачи?
 1. Примеры задач линейного программирования. 1. 1. Задача составления рациона (слайд 4). 1. Неизвестными являются содержание в смеси кормов. Отсюда переменные задачи : - содержание известняка в смеси; - содержание зерна в смеси; - содержание соевых бобов в смеси. 2. Критерием эффективности при сравнении различных вариантов рациона служит стоимость смеси. Следовательно, целевая функция задачи будет иметь вид:
1. Примеры задач линейного программирования. 1. 1. Задача составления рациона (слайд 4). 1. Неизвестными являются содержание в смеси кормов. Отсюда переменные задачи : - содержание известняка в смеси; - содержание зерна в смеси; - содержание соевых бобов в смеси. 2. Критерием эффективности при сравнении различных вариантов рациона служит стоимость смеси. Следовательно, целевая функция задачи будет иметь вид:
 1. Примеры задач линейного программирования. 1. 1. Задача составления рациона (слайд 5). 3. Содержательный смысл ограничений. 1). Ограничение на минимальный недельный рацион для всего поголовья 2). Смесь должна содержать не менее 0. 8% кальция 3). Смесь должна содержать не более 1. 2% кальция 4). Смесь должна содержать не менее 22% белка 5). Смесь должна содержать не более 5% клетчатки
1. Примеры задач линейного программирования. 1. 1. Задача составления рациона (слайд 5). 3. Содержательный смысл ограничений. 1). Ограничение на минимальный недельный рацион для всего поголовья 2). Смесь должна содержать не менее 0. 8% кальция 3). Смесь должна содержать не более 1. 2% кальция 4). Смесь должна содержать не менее 22% белка 5). Смесь должна содержать не более 5% клетчатки
 1. Примеры задач линейного программирования. 1. 1. Задача составления рациона (слайд 6). После преобразования система ограничений будет иметь вид:
1. Примеры задач линейного программирования. 1. 1. Задача составления рациона (слайд 6). После преобразования система ограничений будет иметь вид:
 1. Примеры задач линейного программирования. 1. 2. Задача использования ресурсов (слайд 1). Содержательная постановка задачи Для отделочных работ поступает мраморная крошка 3 -х видов и цветной цемент в количестве 50 т. , 30 т. , 40 т. , 30 т. . Эти материалы используются для приготовления 2 -х видов облицовочных растворов. Растворы получают при смешивании компонентов в пропорциях 2: 3: 2: 1: 2 и 2: 1: 4. Последний член пропорции приходится на прочие материалы, которые поступают без ограничения. Определить оптимальный план приготовления облицовочных растворов, при котором достигается минимум стоимости неиспользованных материалов, если стоимость 1 т материалов соответственно равна 500, 800, 300, 100 рублям.
1. Примеры задач линейного программирования. 1. 2. Задача использования ресурсов (слайд 1). Содержательная постановка задачи Для отделочных работ поступает мраморная крошка 3 -х видов и цветной цемент в количестве 50 т. , 30 т. , 40 т. , 30 т. . Эти материалы используются для приготовления 2 -х видов облицовочных растворов. Растворы получают при смешивании компонентов в пропорциях 2: 3: 2: 1: 2 и 2: 1: 4. Последний член пропорции приходится на прочие материалы, которые поступают без ограничения. Определить оптимальный план приготовления облицовочных растворов, при котором достигается минимум стоимости неиспользованных материалов, если стоимость 1 т материалов соответственно равна 500, 800, 300, 100 рублям.
 1. Примеры задач линейного программирования. 1. 2. Задача использования ресурсов (слайд 2). Предварительный расчет параметров : Где, - стоимость материалов, идущих на приготовление 1 т растворов - общая стоимость материалов
1. Примеры задач линейного программирования. 1. 2. Задача использования ресурсов (слайд 2). Предварительный расчет параметров : Где, - стоимость материалов, идущих на приготовление 1 т растворов - общая стоимость материалов
 1. Примеры задач линейного программирования. 1. 2. Задача использования ресурсов (слайд 3). План приготовления растворов включает две переменные: - количество раствора первого вида - количество раствора второго вида. Целевая функция задачи
1. Примеры задач линейного программирования. 1. 2. Задача использования ресурсов (слайд 3). План приготовления растворов включает две переменные: - количество раствора первого вида - количество раствора второго вида. Целевая функция задачи
 1. Примеры задач линейного программирования. 1. 2. Задача использования ресурсов (слайд 4). Система ограничений включает один тип ограничений ограничения по ресурсам, то есть расход всех имеющихся ресурсов не должен превышать их количество
1. Примеры задач линейного программирования. 1. 2. Задача использования ресурсов (слайд 4). Система ограничений включает один тип ограничений ограничения по ресурсам, то есть расход всех имеющихся ресурсов не должен превышать их количество
 2. Эквивалентные формы записи модели линейного программирования (слайд 1). Стандартной задачей называется следующая форма записи задачи ЛП. Среди всех неотрицательных решений, удовлетворяющих системе линейных неравенств, выбрать такое, при котором линейная форма принимает минимальное значение
2. Эквивалентные формы записи модели линейного программирования (слайд 1). Стандартной задачей называется следующая форма записи задачи ЛП. Среди всех неотрицательных решений, удовлетворяющих системе линейных неравенств, выбрать такое, при котором линейная форма принимает минимальное значение
 2. Эквивалентные формы записи модели линейного программирования (слайд 2) Канонической задачей называется следующая форма записи задачи ЛП. Среди всех неотрицательных решений системы уравнений выбрать такое, при котором линейная форма принимает минимальное значение
2. Эквивалентные формы записи модели линейного программирования (слайд 2) Канонической задачей называется следующая форма записи задачи ЛП. Среди всех неотрицательных решений системы уравнений выбрать такое, при котором линейная форма принимает минимальное значение
 3. Основные приемы перехода от произвольной записи модели к стандартной и канонической форме записи (слайд 1). 1. Переход от неравенства типа к неравенству осуществляется умножением неравенства на 1. Например, неравенства эквивалентны. 2. Переход от задачи на отыскание максимума к задаче на отыскание минимума осуществляется умножением целевой функции на 1. Например, функция достигает максимального значения при тех же значениях неизвестных, что и функция достигает минимального значения.
3. Основные приемы перехода от произвольной записи модели к стандартной и канонической форме записи (слайд 1). 1. Переход от неравенства типа к неравенству осуществляется умножением неравенства на 1. Например, неравенства эквивалентны. 2. Переход от задачи на отыскание максимума к задаче на отыскание минимума осуществляется умножением целевой функции на 1. Например, функция достигает максимального значения при тех же значениях неизвестных, что и функция достигает минимального значения.
 3. Основные приемы перехода от произвольной записи модели к стандартной и канонической форме записи (слайд 2). 3. Переход от неравенства к равенству. Этот переход основан на том, что в задаче ЛП принято, что все переменные. Рассмотрим общий вид неравенства Перенесем свободный член в левую часть неравенства Обозначим левую часть через Последнее уравнение совместно c требованием не отрицательности переменной будет эквивалентно исходному неравенству. Переход от равенств к неравенствам осуществляется в обратном порядке.
3. Основные приемы перехода от произвольной записи модели к стандартной и канонической форме записи (слайд 2). 3. Переход от неравенства к равенству. Этот переход основан на том, что в задаче ЛП принято, что все переменные. Рассмотрим общий вид неравенства Перенесем свободный член в левую часть неравенства Обозначим левую часть через Последнее уравнение совместно c требованием не отрицательности переменной будет эквивалентно исходному неравенству. Переход от равенств к неравенствам осуществляется в обратном порядке.
 Лекция 3 Тема: Основы линейного программирования. Графическое решение задачи линейного программирования. Рассматриваются вопросы: 1. Решение задачи линейного программирования графическим способом. 2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 1. Анализ чувствительности к изменению правых частей ограничений; 2. 2. Анализ ценности ресурсов; 2. 3. Анализ чувствительности к изменению коэффициентов целевой функции.
Лекция 3 Тема: Основы линейного программирования. Графическое решение задачи линейного программирования. Рассматриваются вопросы: 1. Решение задачи линейного программирования графическим способом. 2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 1. Анализ чувствительности к изменению правых частей ограничений; 2. 2. Анализ ценности ресурсов; 2. 3. Анализ чувствительности к изменению коэффициентов целевой функции.
 1. Решение задачи линейного программирования графическим способом (слайд 1). 1 -й этап. Перейти к стандартной форме записи модели. Если число переменных в системе ограничений равно двум, то такая задача ЛП может быть решена графически. 2 -й этап. Производится графическое построение области допустимых решений (ОДР) системы ограничений задачи. Рассмотрим одно из неравенств системы ограничений Приравняем нулю левую часть неравенства. Получим уравнение прямой , которая может быть построена на плоскости X 1 OX 2
1. Решение задачи линейного программирования графическим способом (слайд 1). 1 -й этап. Перейти к стандартной форме записи модели. Если число переменных в системе ограничений равно двум, то такая задача ЛП может быть решена графически. 2 -й этап. Производится графическое построение области допустимых решений (ОДР) системы ограничений задачи. Рассмотрим одно из неравенств системы ограничений Приравняем нулю левую часть неравенства. Получим уравнение прямой , которая может быть построена на плоскости X 1 OX 2
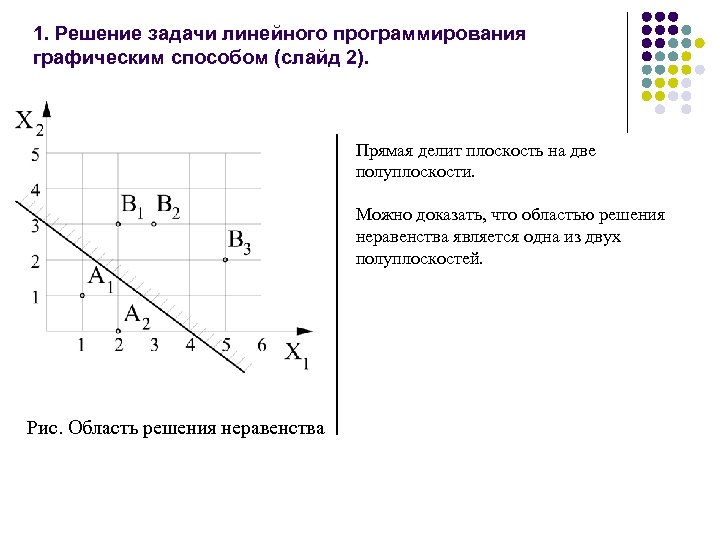 1. Решение задачи линейного программирования графическим способом (слайд 2). Прямая делит плоскость на две полуплоскости. Можно доказать, что областью решения неравенства является одна из двух полуплоскостей. Рис. Область решения неравенства
1. Решение задачи линейного программирования графическим способом (слайд 2). Прямая делит плоскость на две полуплоскости. Можно доказать, что областью решения неравенства является одна из двух полуплоскостей. Рис. Область решения неравенства
 1. Решение задачи линейного программирования графическим способом (слайд 3). При построении ОДР могут возникнуть три случая: 1. замкнутая область; 2. разомкнутая область; 3. противоречивая область. Примеры ОДР системы ограничений
1. Решение задачи линейного программирования графическим способом (слайд 3). При построении ОДР могут возникнуть три случая: 1. замкнутая область; 2. разомкнутая область; 3. противоречивая область. Примеры ОДР системы ограничений
 1. Решение задачи линейного программирования графическим способом (слайд 4). 3 -ий этап. Дается геометрическая интерпретация целевой функции и определяется оптимальное решение задачи. Рассмотрим целевую функцию: Различным значениям целевой функции соответствует семейство параллельных прямых. При перемещении прямой в направлении вектора целевая функция будет возрастать, а в направлении убывать. Рис. Положение прямой, ассоциированной с целевой функцией при различных значениях С
1. Решение задачи линейного программирования графическим способом (слайд 4). 3 -ий этап. Дается геометрическая интерпретация целевой функции и определяется оптимальное решение задачи. Рассмотрим целевую функцию: Различным значениям целевой функции соответствует семейство параллельных прямых. При перемещении прямой в направлении вектора целевая функция будет возрастать, а в направлении убывать. Рис. Положение прямой, ассоциированной с целевой функцией при различных значениях С
 1. Решение задачи линейного программирования графическим способом (слайд 5). Рассмотрим примеры графической интерпретации целевой функции
1. Решение задачи линейного программирования графическим способом (слайд 5). Рассмотрим примеры графической интерпретации целевой функции
 1. Решение задачи линейного программирования графическим способом (слайд 6). Очевидно, решение достигается в одной из вершин ОДР. Координаты этой вершины определяют значение переменных в точке оптимума . Рис. Графическое решение задачи линейного программирования Рассмотрим пример графического решения задачи распределения ресурсов, частная формулировка которой была приведена выше. Из рисунка легко определить оптимальное решение . Подставляя полученные значения переменных в выражение целевой функции, определяем оптимальное значение целевой функции .
1. Решение задачи линейного программирования графическим способом (слайд 6). Очевидно, решение достигается в одной из вершин ОДР. Координаты этой вершины определяют значение переменных в точке оптимума . Рис. Графическое решение задачи линейного программирования Рассмотрим пример графического решения задачи распределения ресурсов, частная формулировка которой была приведена выше. Из рисунка легко определить оптимальное решение . Подставляя полученные значения переменных в выражение целевой функции, определяем оптимальное значение целевой функции .
 2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 1. Анализ чувствительности к изменению правых частей ограничений (слайд 1). Оптимальное решение достигается в точке Рис. Графическая интерпретация задачи
2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 1. Анализ чувствительности к изменению правых частей ограничений (слайд 1). Оптимальное решение достигается в точке Рис. Графическая интерпретация задачи
 2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 1. Анализ чувствительности к изменению правых частей ограничений (слайд 2). Таблица Значения целевой функции в особых точках Точка 8 1 25 7 0 21 5 0 15 6 2 20 При анализе правых частей ставится два вопроса: 1. На сколько можно увеличить запас некоторого ресурса для улучшения полученного оптимального значения целевой функции (при сохранении оптимального базиса)? 2. На сколько можно снизить запас некоторого ресурса (при сохранении оптимального базиса)?
2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 1. Анализ чувствительности к изменению правых частей ограничений (слайд 2). Таблица Значения целевой функции в особых точках Точка 8 1 25 7 0 21 5 0 15 6 2 20 При анализе правых частей ставится два вопроса: 1. На сколько можно увеличить запас некоторого ресурса для улучшения полученного оптимального значения целевой функции (при сохранении оптимального базиса)? 2. На сколько можно снизить запас некоторого ресурса (при сохранении оптимального базиса)?
 2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 1. Анализ чувствительности к изменению правых частей ограничений (слайд 3). Прежде всего необходимо классифицировать ограничения на связывающие (активные) и не связывающие (неактивные). Прямая, соответствующая связывающему ограничению, должна проходить через оптимальное решение. Если некоторое ограничение является связывающим, то соответствующий ресурс расходуется полностью и называется дефицитным ресурсом. Ресурсы, c которыми ассоциируются не связывающие ограничения, относятся к разряду недефицитных (т. е. имеются в некотором избытке). В рассматриваемом примере ограничения (2), (4) соответствуют дефицитным ресурсам, а (1), (3) недефицитным ресурсам.
2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 1. Анализ чувствительности к изменению правых частей ограничений (слайд 3). Прежде всего необходимо классифицировать ограничения на связывающие (активные) и не связывающие (неактивные). Прямая, соответствующая связывающему ограничению, должна проходить через оптимальное решение. Если некоторое ограничение является связывающим, то соответствующий ресурс расходуется полностью и называется дефицитным ресурсом. Ресурсы, c которыми ассоциируются не связывающие ограничения, относятся к разряду недефицитных (т. е. имеются в некотором избытке). В рассматриваемом примере ограничения (2), (4) соответствуют дефицитным ресурсам, а (1), (3) недефицитным ресурсам.
 2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 1. Анализ чувствительности к изменению правых частей ограничений (слайд 4). Верхний уровень изменения дефицитного ресурса (2) определим, подставив координаты точки K в левую часть ограничения (2) Проделав аналогичные выкладки определим верхний уровень изменения дефицитного ресурса (4) (точка R). Проанализируем, к чему приведет сокращение дефицитного ресурса. Очевидно, что никакого улучшения оптимального решения не будет. Интерес представляет характер изменения (уменьшения) целевой функции при сокращении дефицитного ресурса.
2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 1. Анализ чувствительности к изменению правых частей ограничений (слайд 4). Верхний уровень изменения дефицитного ресурса (2) определим, подставив координаты точки K в левую часть ограничения (2) Проделав аналогичные выкладки определим верхний уровень изменения дефицитного ресурса (4) (точка R). Проанализируем, к чему приведет сокращение дефицитного ресурса. Очевидно, что никакого улучшения оптимального решения не будет. Интерес представляет характер изменения (уменьшения) целевой функции при сокращении дефицитного ресурса.
 2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 1. Анализ чувствительности к изменению правых частей ограничений (слайд 5). Рис. Зависимость целевой функции от изменения правых частей ограничений
2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 1. Анализ чувствительности к изменению правых частей ограничений (слайд 5). Рис. Зависимость целевой функции от изменения правых частей ограничений
 2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 1. Анализ чувствительности к изменению правых частей ограничений (слайд 6). Рассмотрим дефицитный ресурс, ассоциированный со 2 м ограничением. При сокращении ресурса прямая (2) будет параллельно перемещаться, но только в другом направлении. Вычислив значение целевой функции для нескольких бли жайших начений ресурсов, можно убедиться, что характер изменения целевой з функции не изменится. Однако, при достижении точки Е характер изменения целевой функции изменится. Поэтому значение ресурса, при котором характер зависимости начинает изменяться, будем считать нижним пределом изменения ресурса. Изменение характера зависимости происходит за счет изменения структуры дефицитных ресурсов. Определим предельный нижний уровень изменения 2 го ресурса
2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 1. Анализ чувствительности к изменению правых частей ограничений (слайд 6). Рассмотрим дефицитный ресурс, ассоциированный со 2 м ограничением. При сокращении ресурса прямая (2) будет параллельно перемещаться, но только в другом направлении. Вычислив значение целевой функции для нескольких бли жайших начений ресурсов, можно убедиться, что характер изменения целевой з функции не изменится. Однако, при достижении точки Е характер изменения целевой функции изменится. Поэтому значение ресурса, при котором характер зависимости начинает изменяться, будем считать нижним пределом изменения ресурса. Изменение характера зависимости происходит за счет изменения структуры дефицитных ресурсов. Определим предельный нижний уровень изменения 2 го ресурса
 2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 1. Анализ чувствительности к изменению правых частей ограничений (слайд 7). Аналогично можно определить нижний предел изменения дефицитного ресурса, ассоциированного c 4 м ограничением. Для него происходит изменение структуры дефицитных ресурсов в точке C. Вместо 4 го ресурса становится дефицитным 1 й. Следовательно, пределы изменения дефицитных ресурсов можно записать в виде:
2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 1. Анализ чувствительности к изменению правых частей ограничений (слайд 7). Аналогично можно определить нижний предел изменения дефицитного ресурса, ассоциированного c 4 м ограничением. Для него происходит изменение структуры дефицитных ресурсов в точке C. Вместо 4 го ресурса становится дефицитным 1 й. Следовательно, пределы изменения дефицитных ресурсов можно записать в виде:
 2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 1. Анализ чувствительности к изменению правых частей ограничений (слайд 8). Рассмотрим теперь недефицитные ресурсы (1) и (3). Увеличение недефицитного ресурса не влияет на значение целевой функции, поскольку это приводит к тому, что избыточный ресурс становится еще более избыточным. Таким образом, Однако, при уменьшении недефицитного ресурса может наступить момент, когда такой ресурс станет дефицитным. Такая ситуация возникает, когда прямая, ассоциированная c недефицитным ресурсом, при параллельном перемещении достигает точки оптимума. Координаты точки D известны. Отсюда легко определить предельный нижний уровень недефицитного ресурса.
2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 1. Анализ чувствительности к изменению правых частей ограничений (слайд 8). Рассмотрим теперь недефицитные ресурсы (1) и (3). Увеличение недефицитного ресурса не влияет на значение целевой функции, поскольку это приводит к тому, что избыточный ресурс становится еще более избыточным. Таким образом, Однако, при уменьшении недефицитного ресурса может наступить момент, когда такой ресурс станет дефицитным. Такая ситуация возникает, когда прямая, ассоциированная c недефицитным ресурсом, при параллельном перемещении достигает точки оптимума. Координаты точки D известны. Отсюда легко определить предельный нижний уровень недефицитного ресурса.
 2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 2. Анализ ценности ресурсов. Этот анализ позволяет ответить на вопрос: увеличение какого из ресурсов наиболее выгодно. т. е. какому из ресурсов отдать предпочтение при вложении дополнительных средств. Этот анализ легко произвести, оперируя данными, полученными в предыдущем пункте анализа. Таким образом, ценность недефицитных ресурсов равна нулю. Ценность дефицитного ресурса (2) больше ценности дефицитного ресурса (4).
2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 2. Анализ ценности ресурсов. Этот анализ позволяет ответить на вопрос: увеличение какого из ресурсов наиболее выгодно. т. е. какому из ресурсов отдать предпочтение при вложении дополнительных средств. Этот анализ легко произвести, оперируя данными, полученными в предыдущем пункте анализа. Таким образом, ценность недефицитных ресурсов равна нулю. Ценность дефицитного ресурса (2) больше ценности дефицитного ресурса (4).
 2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 3. Анализ чувствительности к изменению коэффициентов целевой функции (слайд 1). В этом анализе ставится вопрос: в каких пределах могут изменяться коэффициенты целевой функции, в которых не происходит изменения оптимального решения. При изменении коэффициентов целевой функции изменяется наклон прямой, ассоциированной c ней. Оптимальное решение будет сохраняться до тех пор, пока прямая целевой функции будет проходить через одну и ту же опорную вершину ОДР. Однако при изменении одного из коэффициентов целевой функции может сложиться ситуация, когда оптимальное решение сместится в одну из соседних вершин. А это, в свою очередь, повлечет изменение статуса некоторых ресурсов. Существует минимальное и максимальное значение коэффициентов целевой функции, при котором оптимальные значения переменных не изменятся.
2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 3. Анализ чувствительности к изменению коэффициентов целевой функции (слайд 1). В этом анализе ставится вопрос: в каких пределах могут изменяться коэффициенты целевой функции, в которых не происходит изменения оптимального решения. При изменении коэффициентов целевой функции изменяется наклон прямой, ассоциированной c ней. Оптимальное решение будет сохраняться до тех пор, пока прямая целевой функции будет проходить через одну и ту же опорную вершину ОДР. Однако при изменении одного из коэффициентов целевой функции может сложиться ситуация, когда оптимальное решение сместится в одну из соседних вершин. А это, в свою очередь, повлечет изменение статуса некоторых ресурсов. Существует минимальное и максимальное значение коэффициентов целевой функции, при котором оптимальные значения переменных не изменятся.
 2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 3. Анализ чувствительности к изменению коэффициентов целевой функции (слайд 2). Найдем интервал изменения для c 1 коэффициента при x 1. Поскольку изменение коэффициентов c 1 и c 2 влияет только на наклон прямой L, то целесообразно рассматривать уравнение (в примере ). Введем приращение для c 1. и перепишем уравнение в в В рассматриваемом примере
2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 3. Анализ чувствительности к изменению коэффициентов целевой функции (слайд 2). Найдем интервал изменения для c 1 коэффициента при x 1. Поскольку изменение коэффициентов c 1 и c 2 влияет только на наклон прямой L, то целесообразно рассматривать уравнение (в примере ). Введем приращение для c 1. и перепишем уравнение в в В рассматриваемом примере
 2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 3. Анализ чувствительности к изменению коэффициентов целевой функции (слайд 3). Проанализируем уравнение для нашего примера, используя графическую интерпретацию. Если будет принимать отрицательные значения, то прямая L будет поворачиваться вокруг оси, расположенной в точке D в направлении A-A. Оптимальные значения переменных не изменятся, пока не появится альтернативное решение в точке C. При дальнейшем уменьшении коэффициента при x 1 оптимальное решение изменится. Такая ситуация сложится, когда прямая L займет положение прямой, ассоциированной со вторым ограничением. Следовательно, для того, чтобы найти необходимо приравнять коэффициент при x 1 (тангенс угла наклона прямой L) из последнего уравнения, соответствующему коэффициенту уравнения прямой, ассоциированной со вторым ограничением. Уравнение прямой, ассоциированной со вторым ограничением C учетом знака приращения будем иметь
2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 3. Анализ чувствительности к изменению коэффициентов целевой функции (слайд 3). Проанализируем уравнение для нашего примера, используя графическую интерпретацию. Если будет принимать отрицательные значения, то прямая L будет поворачиваться вокруг оси, расположенной в точке D в направлении A-A. Оптимальные значения переменных не изменятся, пока не появится альтернативное решение в точке C. При дальнейшем уменьшении коэффициента при x 1 оптимальное решение изменится. Такая ситуация сложится, когда прямая L займет положение прямой, ассоциированной со вторым ограничением. Следовательно, для того, чтобы найти необходимо приравнять коэффициент при x 1 (тангенс угла наклона прямой L) из последнего уравнения, соответствующему коэффициенту уравнения прямой, ассоциированной со вторым ограничением. Уравнение прямой, ассоциированной со вторым ограничением C учетом знака приращения будем иметь
 2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 3. Анализ чувствительности к изменению коэффициентов целевой функции (слайд 4). При увеличении прямая L , будет поворачиваться вокруг оси, расположенной в точке D в направлении B-B. Однако, альтернативное решение не появляется. Если устремить к бесконечности, то наклон прямой приближается к 90 градусам. Следовательно, а пределы изменения с1: Аналогично можно определить и пределы изменения коэффициента c 2 : .
2. Анализ на чувствительность задачи линейного программирования графическим способом 2. 3. Анализ чувствительности к изменению коэффициентов целевой функции (слайд 4). При увеличении прямая L , будет поворачиваться вокруг оси, расположенной в точке D в направлении B-B. Однако, альтернативное решение не появляется. Если устремить к бесконечности, то наклон прямой приближается к 90 градусам. Следовательно, а пределы изменения с1: Аналогично можно определить и пределы изменения коэффициента c 2 : .
 Лекция 4 Тема: Симплекс-метод решения задач линейного программирования Рассматриваются вопросы: 1. 2. 3. 4. 5. 6. Симплекс процесс. Симплекс таблица. Отыскание оптимального решения симплекс методом. Методы поиска опорного решения. 4. 1. Алгоритм 1. 4. 2. Метод больших штрафов.
Лекция 4 Тема: Симплекс-метод решения задач линейного программирования Рассматриваются вопросы: 1. 2. 3. 4. 5. 6. Симплекс процесс. Симплекс таблица. Отыскание оптимального решения симплекс методом. Методы поиска опорного решения. 4. 1. Алгоритм 1. 4. 2. Метод больших штрафов.
 1. Симплекс-процесс (слайд 1). Симплекс метод это алгебраический аппарат решения задачи ЛП. Рассмотрим пример
1. Симплекс-процесс (слайд 1). Симплекс метод это алгебраический аппарат решения задачи ЛП. Рассмотрим пример
 1. Симплекс-процесс (слайд 2). Экстре мальные точки Нулевые переменные Ненулевые переменные Значение целе вой функции O A B C D E x 1, x 2, S 1, S 4, S 3, x 1 S 1, S 2, S 3, S 4 x 2, S 1, S 3, S 4 x 1, x 2, S 3 x 1, x 2, S 1, S 2, S 4 0 6 16 17 6
1. Симплекс-процесс (слайд 2). Экстре мальные точки Нулевые переменные Ненулевые переменные Значение целе вой функции O A B C D E x 1, x 2, S 1, S 4, S 3, x 1 S 1, S 2, S 3, S 4 x 2, S 1, S 3, S 4 x 1, x 2, S 3 x 1, x 2, S 1, S 2, S 4 0 6 16 17 6
 1. Симплекс-процесс (слайд 3). Выводы: 1. Решение задачи, если оно существует, лежит в одной из вершин ОДР ( в частном случае множество точек одной из граней ОДР). Следовательно оно может быть найдено полным перебором вершин ОДР. Решение, расположенное в вершине ОДР, называется опорным. 2. В опорных вершинах k=n-m переменных равны нулю (n число переменных задачи, m число уравнений, k числo свободных переменных). 3. Смежные опорные вершины отличаются только одной переменной в каждой группе (нулевых и ненулевых переменных). Следовательно, чтобы осуществить переход от одной вершины к другой, необходимо произвести замену переменных.
1. Симплекс-процесс (слайд 3). Выводы: 1. Решение задачи, если оно существует, лежит в одной из вершин ОДР ( в частном случае множество точек одной из граней ОДР). Следовательно оно может быть найдено полным перебором вершин ОДР. Решение, расположенное в вершине ОДР, называется опорным. 2. В опорных вершинах k=n-m переменных равны нулю (n число переменных задачи, m число уравнений, k числo свободных переменных). 3. Смежные опорные вершины отличаются только одной переменной в каждой группе (нулевых и ненулевых переменных). Следовательно, чтобы осуществить переход от одной вершины к другой, необходимо произвести замену переменных.
 1. Симплекс-процесс (слайд 4). Запишем стандартную задачу в общем виде: Введем остаточные переменные и перепишем задачу в виде:
1. Симплекс-процесс (слайд 4). Запишем стандартную задачу в общем виде: Введем остаточные переменные и перепишем задачу в виде:
 1. Симплекс-процесс (слайд 5). В последней системе ограничений x 1, x 2, . . . , xk свободные переменные. Проанализируем, что произойдет, если эти переменные приравнять нулю. Получим: Это решение может быть допустимым или недопустимым. Оно допустимо, если все свободные члены неотрицательны. Предположим, что это условие выполнено, тогда получим опорное решение. Проверим, является ли оно оптимальным. Очевидно, что при . Возможно ли улучшить решение, т. е. уменьшить функцию L? Уменьшить L можно только увеличивая какие нибудь из переменных x 1, x 2, . . . , xk (уменьшать их нельзя, т. к. все они равны нулю, а отрицательные значения переменных не допустимы). Если все коэффициенты в выражении целевой функции положительны, то, увеличивая какие то из переменныx x 1, x 2, . . . , xk сверх нуля , невозможно уменьшить L. Следовательно, найденное опорное решение является оптимальным. Если среди коэффициентов есть отрицательные, то, увеличивая соответствующие переменные, можно улучшить решение, т. е. уменьшить L.
1. Симплекс-процесс (слайд 5). В последней системе ограничений x 1, x 2, . . . , xk свободные переменные. Проанализируем, что произойдет, если эти переменные приравнять нулю. Получим: Это решение может быть допустимым или недопустимым. Оно допустимо, если все свободные члены неотрицательны. Предположим, что это условие выполнено, тогда получим опорное решение. Проверим, является ли оно оптимальным. Очевидно, что при . Возможно ли улучшить решение, т. е. уменьшить функцию L? Уменьшить L можно только увеличивая какие нибудь из переменных x 1, x 2, . . . , xk (уменьшать их нельзя, т. к. все они равны нулю, а отрицательные значения переменных не допустимы). Если все коэффициенты в выражении целевой функции положительны, то, увеличивая какие то из переменныx x 1, x 2, . . . , xk сверх нуля , невозможно уменьшить L. Следовательно, найденное опорное решение является оптимальным. Если среди коэффициентов есть отрицательные, то, увеличивая соответствующие переменные, можно улучшить решение, т. е. уменьшить L.
 1. Симплекс-процесс (слайд 6). Пусть, например, коэффициент отрицателен. Значит имеет смысл увеличивать x 1, т. е. перейти от данного опорного решения к другому, где переменная x 1 не равна нулю, а вместо нее равна нулю какая то другая. Однако, увеличивать x 1 можно до тех пор, пока не станет отрицательной одна из базисных переменных . Если среди ограничений нет уравнений c положительными коэффициентами при x 1, то значение x 1 можно увеличивать беспредельно, а значит, линейная функция L не ограничена снизу. Допустим, что есть уравнения в которых коэффициенты при x положительны. Возьмем одну из базисных переменных xr, соответствующую такому уравнению и определим до какой степени можно увеличивать x 1, т. е. при каком значении переменной x 1 переменная xr станет равной нулю. Выпишем r ое уравнение в виде: В этом уравнении член и коэффициент ar 1 положителен. Следовательно, если оставить , то x 1 можно увеличивать до значения . При дальнейшем увеличении x 1 переменная xr станет отрицательной.
1. Симплекс-процесс (слайд 6). Пусть, например, коэффициент отрицателен. Значит имеет смысл увеличивать x 1, т. е. перейти от данного опорного решения к другому, где переменная x 1 не равна нулю, а вместо нее равна нулю какая то другая. Однако, увеличивать x 1 можно до тех пор, пока не станет отрицательной одна из базисных переменных . Если среди ограничений нет уравнений c положительными коэффициентами при x 1, то значение x 1 можно увеличивать беспредельно, а значит, линейная функция L не ограничена снизу. Допустим, что есть уравнения в которых коэффициенты при x положительны. Возьмем одну из базисных переменных xr, соответствующую такому уравнению и определим до какой степени можно увеличивать x 1, т. е. при каком значении переменной x 1 переменная xr станет равной нулю. Выпишем r ое уравнение в виде: В этом уравнении член и коэффициент ar 1 положителен. Следовательно, если оставить , то x 1 можно увеличивать до значения . При дальнейшем увеличении x 1 переменная xr станет отрицательной.
 1. Симплекс-процесс (слайд 7). Выберем ту из переменных, которая раньше всех обратится в ноль при увеличении x 1 , т. е. ту для которой величина минимальна. Пусть это будет переменная xi. Тогда имеет смысл переразрешить систему ограничений относительно других базисных переменных, выведя из числа свободных x 1 и переведя в группу свободных вместо нее xi. Предположим, что уравнения для нового набора базисных переменных составлены, тогда приходим к началу описанной процедуры, т. е. произведен один шаг итерационного процесса, который называется симплекс процессом.
1. Симплекс-процесс (слайд 7). Выберем ту из переменных, которая раньше всех обратится в ноль при увеличении x 1 , т. е. ту для которой величина минимальна. Пусть это будет переменная xi. Тогда имеет смысл переразрешить систему ограничений относительно других базисных переменных, выведя из числа свободных x 1 и переведя в группу свободных вместо нее xi. Предположим, что уравнения для нового набора базисных переменных составлены, тогда приходим к началу описанной процедуры, т. е. произведен один шаг итерационного процесса, который называется симплекс процессом.
 2. Симплекс-таблица (слайд 1). где, базисные переменные; x 1, x 2, . . . , xk свободные переменные; m число ограничений задачи; n = m + k число переменных задачи;
2. Симплекс-таблица (слайд 1). где, базисные переменные; x 1, x 2, . . . , xk свободные переменные; m число ограничений задачи; n = m + k число переменных задачи;
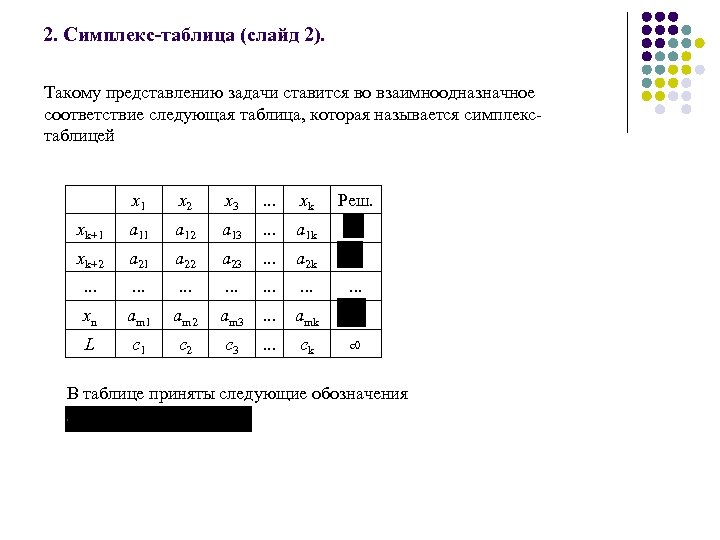 2. Симплекс-таблица (слайд 2). Такому представлению задачи ставится во взаимноодназначное соответствие следующая таблица, которая называется симплекс таблицей x 1 x 2 x 3 . . . xk xk+1 a 12 a 13 . . . a 1 k xk+2 a 21 a 22 a 23 . . . a 2 k . . . . xn am 1 am 2 am 3 . . . amk L c 1 c 2 c 3 . . . ck Реш. . c 0 В таблице приняты следующие обозначения
2. Симплекс-таблица (слайд 2). Такому представлению задачи ставится во взаимноодназначное соответствие следующая таблица, которая называется симплекс таблицей x 1 x 2 x 3 . . . xk xk+1 a 12 a 13 . . . a 1 k xk+2 a 21 a 22 a 23 . . . a 2 k . . . . xn am 1 am 2 am 3 . . . amk L c 1 c 2 c 3 . . . ck Реш. . c 0 В таблице приняты следующие обозначения
 2. Симплекс-таблица (слайд 3). Определения 1. Строка симплекс таблицы, которая соответствует базисной переменной выводимой из базиса, называется разрешающей. 2. Столбец симплекс таблицы, который соответствует свободной переменной вводимой в базис, называется разрешающим столбцом. 3. Элемент симплекс таблицы, стоящий на пересечении разрешающей строки и разрешающего столбца, называется разрешающим. Алгоритм расчета элементов симплекс-таблицы при замене переменных: 1. Элемент "новой" симплекс таблицы, соответствующий разрешающему элементу исходной таблицы, есть величина обратная разрешающему элементу. 2. Все остальные элементы, соответствующие разрешающей строке, рассчитываются как отношение соответствующих элементов исходной таблицы к разрешающему элементу. 3. Все остальные элементы, соответствующие разрешающему столбцу, рассчитываются как отношение соответствующих элементов исходной таблицы к разрешающему элементу c обратным знаком. 4. Все остальные элементы "новой" таблицы рассчитываются по правилу прямоугольника: элемент "новой" симплекс таблицы; элемент исходной симплекс таблицы; разрешающий элемент.
2. Симплекс-таблица (слайд 3). Определения 1. Строка симплекс таблицы, которая соответствует базисной переменной выводимой из базиса, называется разрешающей. 2. Столбец симплекс таблицы, который соответствует свободной переменной вводимой в базис, называется разрешающим столбцом. 3. Элемент симплекс таблицы, стоящий на пересечении разрешающей строки и разрешающего столбца, называется разрешающим. Алгоритм расчета элементов симплекс-таблицы при замене переменных: 1. Элемент "новой" симплекс таблицы, соответствующий разрешающему элементу исходной таблицы, есть величина обратная разрешающему элементу. 2. Все остальные элементы, соответствующие разрешающей строке, рассчитываются как отношение соответствующих элементов исходной таблицы к разрешающему элементу. 3. Все остальные элементы, соответствующие разрешающему столбцу, рассчитываются как отношение соответствующих элементов исходной таблицы к разрешающему элементу c обратным знаком. 4. Все остальные элементы "новой" таблицы рассчитываются по правилу прямоугольника: элемент "новой" симплекс таблицы; элемент исходной симплекс таблицы; разрешающий элемент.
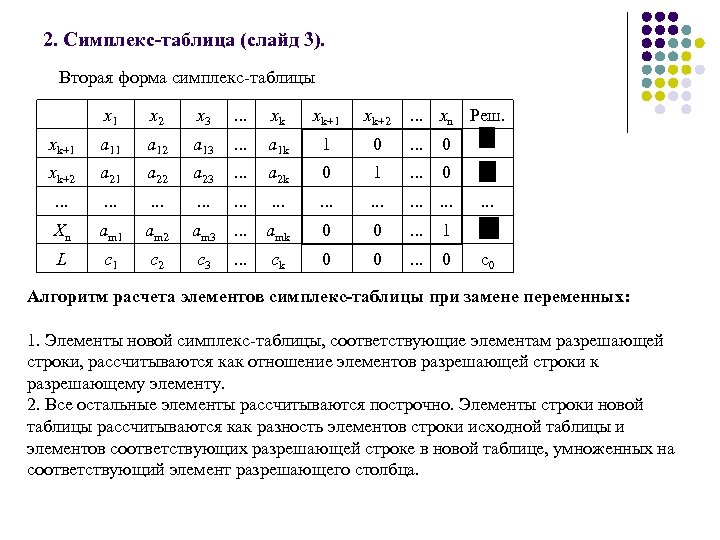 2. Симплекс-таблица (слайд 3). Вторая форма симплекс таблицы x 1 x 2 x 3 . . . xk xk+1 xk+2 . . . xn Реш. xk+1 a 12 a 13 . . . a 1 k 1 0 . . . 0 xk+2 a 21 a 22 a 23 . . . a 2 k 0 1 . . . 0 . . . . Xn am 1 am 2 am 3 . . . amk 0 0 . . . 1 L c 1 c 2 c 3 . . . ck 0 0 . . . c 0 Алгоритм расчета элементов симплекс-таблицы при замене переменных: 1. Элементы новой симплекс таблицы, соответствующие элементам разрешающей строки, рассчитываются как отношение элементов разрешающей строки к разрешающему элементу. 2. Все остальные элементы рассчитываются построчно. Элементы строки новой таблицы рассчитываются как разность элементов строки исходной таблицы и элементов соответствующих разрешающей строке в новой таблице, умноженных на соответствующий элемент разрешающего столбца.
2. Симплекс-таблица (слайд 3). Вторая форма симплекс таблицы x 1 x 2 x 3 . . . xk xk+1 xk+2 . . . xn Реш. xk+1 a 12 a 13 . . . a 1 k 1 0 . . . 0 xk+2 a 21 a 22 a 23 . . . a 2 k 0 1 . . . 0 . . . . Xn am 1 am 2 am 3 . . . amk 0 0 . . . 1 L c 1 c 2 c 3 . . . ck 0 0 . . . c 0 Алгоритм расчета элементов симплекс-таблицы при замене переменных: 1. Элементы новой симплекс таблицы, соответствующие элементам разрешающей строки, рассчитываются как отношение элементов разрешающей строки к разрешающему элементу. 2. Все остальные элементы рассчитываются построчно. Элементы строки новой таблицы рассчитываются как разность элементов строки исходной таблицы и элементов соответствующих разрешающей строке в новой таблице, умноженных на соответствующий элемент разрешающего столбца.
 2. Алгоритм определения оптимального решения. Алгоритм применяется если в симплекс таблице определено опорное решение, т. е. нет отрицательных элементов в столбце свободных членов (столбец решение). Сформулируем алгоритм относительно задачи на отыскание минимума. 1. Рассматривается строка, соответствующая целевой функции. Если среди элементов строки нет положительных элементов, то оптимальное решение достигнуто. Если есть положительный элемент, то любой из них может послужить для выбора разрешающего столбца. 2. Рассматриваются элементы разрешающего столбца. Если среди элементов нет положительных (за исключением строки целевой функции), то целевая функция не ограничена. Если среди элементов есть положительные, вычисляются отношения элементов столбца свободных членов (столбец решение) к таким элементам. Элемент, при котором достигается минимум отношения, выбирается в качестве разрешающего. 3. Рассчитываются элементы новой симплекс таблицы и переходят к пункту 1. Для задачи на максимум алгоритм совпадает c точностью до знака целевой функции.
2. Алгоритм определения оптимального решения. Алгоритм применяется если в симплекс таблице определено опорное решение, т. е. нет отрицательных элементов в столбце свободных членов (столбец решение). Сформулируем алгоритм относительно задачи на отыскание минимума. 1. Рассматривается строка, соответствующая целевой функции. Если среди элементов строки нет положительных элементов, то оптимальное решение достигнуто. Если есть положительный элемент, то любой из них может послужить для выбора разрешающего столбца. 2. Рассматриваются элементы разрешающего столбца. Если среди элементов нет положительных (за исключением строки целевой функции), то целевая функция не ограничена. Если среди элементов есть положительные, вычисляются отношения элементов столбца свободных членов (столбец решение) к таким элементам. Элемент, при котором достигается минимум отношения, выбирается в качестве разрешающего. 3. Рассчитываются элементы новой симплекс таблицы и переходят к пункту 1. Для задачи на максимум алгоритм совпадает c точностью до знака целевой функции.
 3. Алгоритм определения опорного решения - алгоритм 1. Задача определения опорного решения возникает, когда в симплекс таблице среди свободных членов (столбец решение) есть отрицательные элементы. Для первой формы симплекс таблиц используется следующий алгоритм определения опорного решения. 1. Рассматривается строка симплекс таблицы, содержащая отрицательный элемент в столбце решение. Если в этой строке больше нет ни одного отрицательного элемента, то задача линейного программирования не имеет реше ния. Если отрицательный элемент есть, то столбец в котором он расположен выбирается в качестве разрешающего. 2. Вычисляются отношения совпадающих по знаку элементов столбца решение и разрешающего столбца. Элемент, при котором достигается минимум отношения, выбирается в качестве разрешающего. 3. После перехода к новому базису рассматривается столбец свободных членов таблицы. Если среди элементов столбца нет отрицательных то опорное решение найдено, если есть отрицательный, то перейти к пункту 1 алгоритма.
3. Алгоритм определения опорного решения - алгоритм 1. Задача определения опорного решения возникает, когда в симплекс таблице среди свободных членов (столбец решение) есть отрицательные элементы. Для первой формы симплекс таблиц используется следующий алгоритм определения опорного решения. 1. Рассматривается строка симплекс таблицы, содержащая отрицательный элемент в столбце решение. Если в этой строке больше нет ни одного отрицательного элемента, то задача линейного программирования не имеет реше ния. Если отрицательный элемент есть, то столбец в котором он расположен выбирается в качестве разрешающего. 2. Вычисляются отношения совпадающих по знаку элементов столбца решение и разрешающего столбца. Элемент, при котором достигается минимум отношения, выбирается в качестве разрешающего. 3. После перехода к новому базису рассматривается столбец свободных членов таблицы. Если среди элементов столбца нет отрицательных то опорное решение найдено, если есть отрицательный, то перейти к пункту 1 алгоритма.
 3. Алгоритм определения опорного решения методом больших штрафов.
3. Алгоритм определения опорного решения методом больших штрафов.
 Лекция 5 Тема: Симплекс-метод решения задач линейного программирования Рассматриваются вопросы: 1. Анализ на чувствительность задачи линейного программирования табличный алгоритм 1. 1. Анализ чувствительности к изменению правых частей ограничений; 1. 2. Анализ ценности ресурсов; 1. 3. Анализ чувствительности к изменению коэффициентов целевой функции.
Лекция 5 Тема: Симплекс-метод решения задач линейного программирования Рассматриваются вопросы: 1. Анализ на чувствительность задачи линейного программирования табличный алгоритм 1. 1. Анализ чувствительности к изменению правых частей ограничений; 1. 2. Анализ ценности ресурсов; 1. 3. Анализ чувствительности к изменению коэффициентов целевой функции.
 1. 1. Анализ чувствительности к изменению правых частей ограничений –табличный алгоритм (слайд 1).
1. 1. Анализ чувствительности к изменению правых частей ограничений –табличный алгоритм (слайд 1).
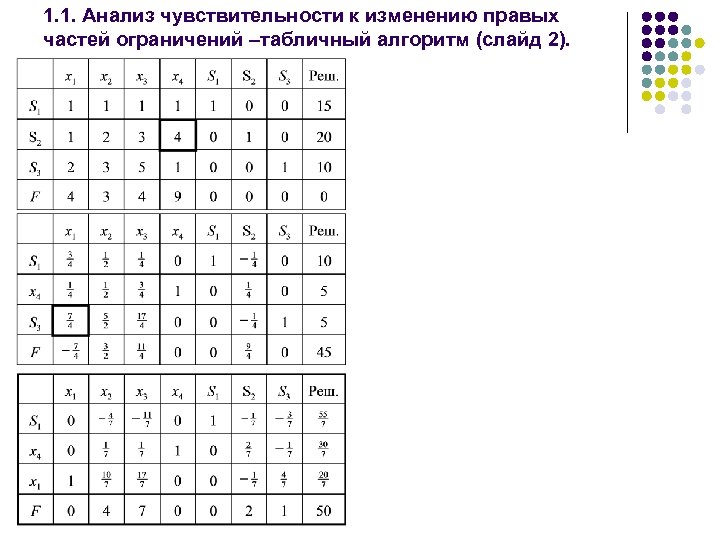 1. 1. Анализ чувствительности к изменению правых частей ограничений –табличный алгоритм (слайд 2).
1. 1. Анализ чувствительности к изменению правых частей ограничений –табличный алгоритм (слайд 2).
 1. 1. Анализ чувствительности к изменению правых частей ограничений –табличный алгоритм (слайд 3).
1. 1. Анализ чувствительности к изменению правых частей ограничений –табличный алгоритм (слайд 3).
 1. 1. Анализ чувствительности к изменению правых частей ограничений –табличный алгоритм (слайд 3).
1. 1. Анализ чувствительности к изменению правых частей ограничений –табличный алгоритм (слайд 3).
 1. 1. Анализ чувствительности к изменению правых частей ограничений –табличный алгоритм (слайд 3).
1. 1. Анализ чувствительности к изменению правых частей ограничений –табличный алгоритм (слайд 3).
 1. 2. Анализ ценности ресурсов –табличный алгоритм.
1. 2. Анализ ценности ресурсов –табличный алгоритм.
 1. 3. Анализ чувствительности к изменению коэффициентов целевой функции - табличный алгоритм
1. 3. Анализ чувствительности к изменению коэффициентов целевой функции - табличный алгоритм
 1. 3. Анализ чувствительности к изменению коэффициентов целевой функции - табличный алгоритм
1. 3. Анализ чувствительности к изменению коэффициентов целевой функции - табличный алгоритм
 Лекция 6 Тема: Транспортная задача Рассматриваются вопросы: 1. 2. 3. 4. 5. Математическая модель транспортной задачи. Особенности транспортной задачи. Поиск опорного решения методом северо-западного угла. Поиск опорного решения методом минимального элемента. Поиск опорного решения методом Фогеля.
Лекция 6 Тема: Транспортная задача Рассматриваются вопросы: 1. 2. 3. 4. 5. Математическая модель транспортной задачи. Особенности транспортной задачи. Поиск опорного решения методом северо-западного угла. Поиск опорного решения методом минимального элемента. Поиск опорного решения методом Фогеля.
 1. Математическая модель транспортной задачи слайд 1).
1. Математическая модель транспортной задачи слайд 1).
 1. Математическая модель транспортной задачи (слайд 2).
1. Математическая модель транспортной задачи (слайд 2).
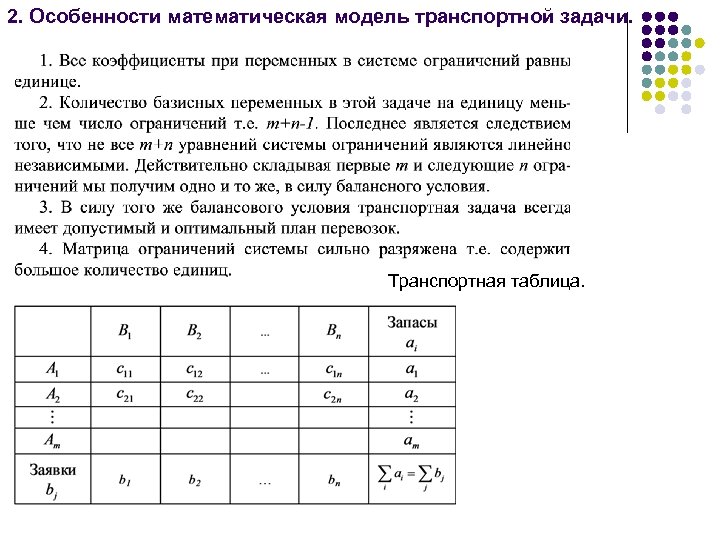 2. Особенности математическая модель транспортной задачи. Транспортная таблица.
2. Особенности математическая модель транспортной задачи. Транспортная таблица.
 3. Поиск опорного решения – метод северо-западного угла. l Переходим в верхний левый угол и устанавливаем x в такое максимальное значение, чтобы полностью исчерпать предложение или удовлетворить спрос. В первом случае вычёркиваем строку, во втором столбец. Если и то, и другое происходит одновременно, вычёркивается только строка или только столбец. l Процесс повторяется, пока невычеркнутым не останется только один столбец или только одна строка.
3. Поиск опорного решения – метод северо-западного угла. l Переходим в верхний левый угол и устанавливаем x в такое максимальное значение, чтобы полностью исчерпать предложение или удовлетворить спрос. В первом случае вычёркиваем строку, во втором столбец. Если и то, и другое происходит одновременно, вычёркивается только строка или только столбец. l Процесс повторяется, пока невычеркнутым не останется только один столбец или только одна строка.
 4. Поиск опорного решения – метод минимального элемента. l В таблице находится ячейка с минимальной стоимостью. Х в этой ячейка присваивается максимально допустимое ограничениями значение. Соответствующая строка или столбец вычёркивается. l Процесс повторяется, пока невычеркнутым не останется только один столбец или только одна строка.
4. Поиск опорного решения – метод минимального элемента. l В таблице находится ячейка с минимальной стоимостью. Х в этой ячейка присваивается максимально допустимое ограничениями значение. Соответствующая строка или столбец вычёркивается. l Процесс повторяется, пока невычеркнутым не останется только один столбец или только одна строка.
 5. Поиск опорного решения – метод Фогеля. 1. 2. 3. l l Для каждой строки (столбца), которой соответствует положительное предложение (спрос), вычисляется штраф путём вычитания минимальной стоимости из следующей по величине в данной строке (столбце). Выделяется строка с максимальным штрафом (если их несколько, выбор произволен). Из этой строки выбирается переменная с максимальной стоимостью и ей присваивается максимальное допустимое ограничениями значение. Затем в соответствии с присвоенным значением переменной корректируются размеры неудовлетворённого спроса и нереализованного предложения. Строка или столбец, соответствующие выполненному ограничению, вычёркиваются. Если ограничения на спрос и предложения выполняются одновременно, вычёркивается ТОЛЬКО строка или ТОЛЬКО столбец, причём оставшейся строке (столбцу) приписывается нулевое предложение (спрос). а) Если не вычеркнута только одна строка (столбец) с нулевым спросом (предложением), вычисления заканчиваются б) Если не вычеркнута только одна строка (столбец) с ненулевым спросом (предложением), в этой строке (столбце) методом минимального элемента находятся базисные переменные и вычисления заканчиваются в) Если всем невычеркнутым строкам и столбцам соответствуют нулевые объёмы предложения и спроса, методом минимального элемента находятся нулевые базисные переменные и вычисления заканчиваются В остальных случаях следует перейти к шагу 1
5. Поиск опорного решения – метод Фогеля. 1. 2. 3. l l Для каждой строки (столбца), которой соответствует положительное предложение (спрос), вычисляется штраф путём вычитания минимальной стоимости из следующей по величине в данной строке (столбце). Выделяется строка с максимальным штрафом (если их несколько, выбор произволен). Из этой строки выбирается переменная с максимальной стоимостью и ей присваивается максимальное допустимое ограничениями значение. Затем в соответствии с присвоенным значением переменной корректируются размеры неудовлетворённого спроса и нереализованного предложения. Строка или столбец, соответствующие выполненному ограничению, вычёркиваются. Если ограничения на спрос и предложения выполняются одновременно, вычёркивается ТОЛЬКО строка или ТОЛЬКО столбец, причём оставшейся строке (столбцу) приписывается нулевое предложение (спрос). а) Если не вычеркнута только одна строка (столбец) с нулевым спросом (предложением), вычисления заканчиваются б) Если не вычеркнута только одна строка (столбец) с ненулевым спросом (предложением), в этой строке (столбце) методом минимального элемента находятся базисные переменные и вычисления заканчиваются в) Если всем невычеркнутым строкам и столбцам соответствуют нулевые объёмы предложения и спроса, методом минимального элемента находятся нулевые базисные переменные и вычисления заканчиваются В остальных случаях следует перейти к шагу 1
 Лекция 7 Тема: Транспортная задача Рассматриваются вопросы: 1. 2. 3. 4. Понятие цикла транспортной задачи. Распределительный метод решения транспортной задачи. Решение транспортной задачи методом потенциалов. Некоторые частные случаи и обобщения транспортной модели.
Лекция 7 Тема: Транспортная задача Рассматриваются вопросы: 1. 2. 3. 4. Понятие цикла транспортной задачи. Распределительный метод решения транспортной задачи. Решение транспортной задачи методом потенциалов. Некоторые частные случаи и обобщения транспортной модели.
 1. Решение транспортной задачи распределительным методом. l Среди небазисных переменных выбирается одна, введение которой в базис позволит улучшить значение целевой функции. Если условия оптимальности выполняются для всех небазисных переменных – вычисления заканчиваются, иначе переходим к следующему шагу. l Определяется исключаемая из базиса переменная. Происходит изменение базиса, затем процесс повторяется.
1. Решение транспортной задачи распределительным методом. l Среди небазисных переменных выбирается одна, введение которой в базис позволит улучшить значение целевой функции. Если условия оптимальности выполняются для всех небазисных переменных – вычисления заканчиваются, иначе переходим к следующему шагу. l Определяется исключаемая из базиса переменная. Происходит изменение базиса, затем процесс повторяется.
 2. Решение транспортной задачи методом потенциалов (слайд 1).
2. Решение транспортной задачи методом потенциалов (слайд 1).
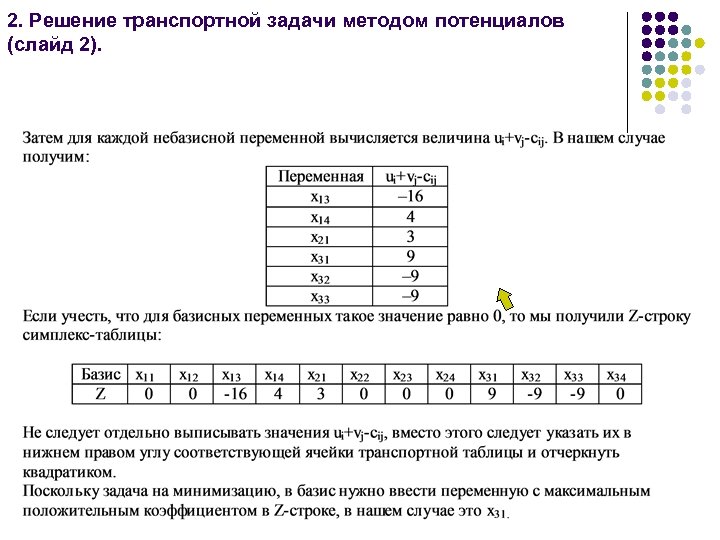 2. Решение транспортной задачи методом потенциалов (слайд 2).
2. Решение транспортной задачи методом потенциалов (слайд 2).
 2. Решение транспортной задачи методом потенциалов (слайд 3).
2. Решение транспортной задачи методом потенциалов (слайд 3).
 2. Решение транспортной задачи методом потенциалов (слайд 4).
2. Решение транспортной задачи методом потенциалов (слайд 4).
 Лекция 8 Тема: Двойственные задачи линейного программирования Рассматриваются вопросы: 1. Определение двойственной задачи. 2. Правила записи двойственной задачи. 3. Примеры записи двойственных задач.
Лекция 8 Тема: Двойственные задачи линейного программирования Рассматриваются вопросы: 1. Определение двойственной задачи. 2. Правила записи двойственной задачи. 3. Примеры записи двойственных задач.
 1. Определение двойственной задачи (слайд 1). l l l Двойственная задача вспомогательная задача ЛП, формулируемая c помощью определенных правил непосредственно из условий исходной (прямой) задачи. В литературе по ЛП в большинстве случаев раccматриваютcя формулировки двойcтвенной задачи, cоответcтвующие различным формам прямой задачи, которые, в свою очередь, определяются типом ограничений, знаками переменных направлением оптимизации. Раccмотрим обобщенную формулировку двойcтвенной задачи ЛП, которая применима к любой форме представления прямой задачи. В основу такой формулировки положен тот факт, что использование cимплекc метода требует приведения любой задачи ЛП к канонической форме. Т. к. все методы вычислений, основанные на соотношениях двойcтвенноcти, предполагают непосредственное использование симплекс таблиц, логично формулировать двойственную задачу в соответствии c канонической формой прямой.
1. Определение двойственной задачи (слайд 1). l l l Двойственная задача вспомогательная задача ЛП, формулируемая c помощью определенных правил непосредственно из условий исходной (прямой) задачи. В литературе по ЛП в большинстве случаев раccматриваютcя формулировки двойcтвенной задачи, cоответcтвующие различным формам прямой задачи, которые, в свою очередь, определяются типом ограничений, знаками переменных направлением оптимизации. Раccмотрим обобщенную формулировку двойcтвенной задачи ЛП, которая применима к любой форме представления прямой задачи. В основу такой формулировки положен тот факт, что использование cимплекc метода требует приведения любой задачи ЛП к канонической форме. Т. к. все методы вычислений, основанные на соотношениях двойcтвенноcти, предполагают непосредственное использование симплекс таблиц, логично формулировать двойственную задачу в соответствии c канонической формой прямой.
 1. Определение двойственной задачи (слайд 2).
1. Определение двойственной задачи (слайд 2).
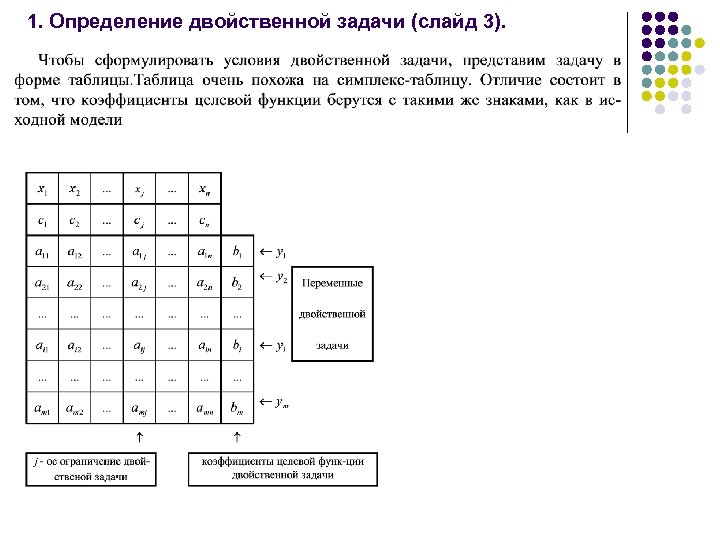 1. Определение двойственной задачи (слайд 3).
1. Определение двойственной задачи (слайд 3).
 2. Правила запиcи двойственных задач (слад 1). 1. Каждому ограничению прямой задачи соответствует переменная двойственной. 2. Каждой переменной прямой задачи соответствует ограничение двойcтвенной задачи. 3. Коэффициенты при некоторой переменной, фигурирующей в ограничениях прямой задачи становятся коэффициентами левой части соответствующего ограничения двойcтвенной задачи, а коэффициент, фигурирующий при той же переменной в выражении для целевой функции прямой задачи, становятся постоянной правой части этого же ограничения двойcтвенной задачи. Если прямая задача имеет n переменных и m ограничений, то двойственная ей задача имеет m переменных и n ограничений.
2. Правила запиcи двойственных задач (слад 1). 1. Каждому ограничению прямой задачи соответствует переменная двойственной. 2. Каждой переменной прямой задачи соответствует ограничение двойcтвенной задачи. 3. Коэффициенты при некоторой переменной, фигурирующей в ограничениях прямой задачи становятся коэффициентами левой части соответствующего ограничения двойcтвенной задачи, а коэффициент, фигурирующий при той же переменной в выражении для целевой функции прямой задачи, становятся постоянной правой части этого же ограничения двойcтвенной задачи. Если прямая задача имеет n переменных и m ограничений, то двойственная ей задача имеет m переменных и n ограничений.
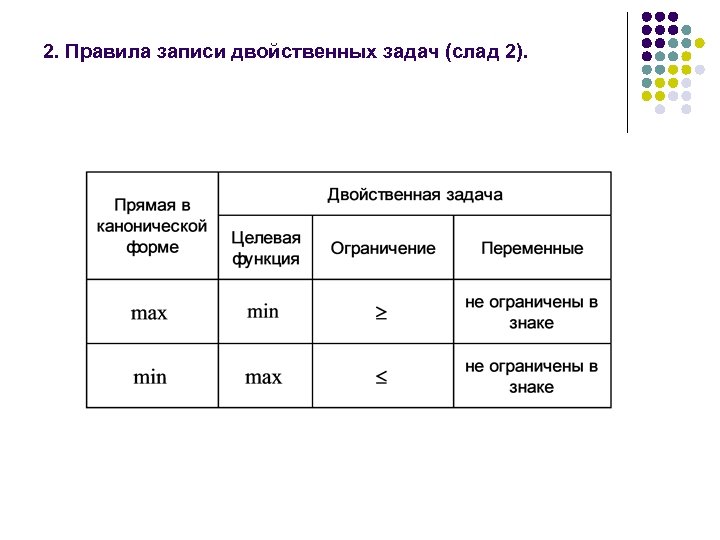 2. Правила запиcи двойственных задач (слад 2).
2. Правила запиcи двойственных задач (слад 2).
 2. Пример записи двойственной задачи 1.
2. Пример записи двойственной задачи 1.
 2. Пример записи двойственной задачи 2.
2. Пример записи двойственной задачи 2.
 Лекция 9 Тема: Двойственные задачи линейного программирования Рассматриваются вопросы: 1. Первая теорема двойственности. 2. Вторая теорема двойственности. 3. Двойственный симплекс-метод.
Лекция 9 Тема: Двойственные задачи линейного программирования Рассматриваются вопросы: 1. Первая теорема двойственности. 2. Вторая теорема двойственности. 3. Двойственный симплекс-метод.
 1. Первая теорема двойственности (слайд 1).
1. Первая теорема двойственности (слайд 1).
 1. Первая теорема двойственности (слайд 2).
1. Первая теорема двойственности (слайд 2).
 2. Первая теорема двойственности - доказательство пунктов б и г (слайд 1).
2. Первая теорема двойственности - доказательство пунктов б и г (слайд 1).
 2. Первая теорема двойственности - доказательство пункта б и г (слайд 1).
2. Первая теорема двойственности - доказательство пункта б и г (слайд 1).
 2. Первая теорема двойственности - доказательство пункта б и г (слайд 1).
2. Первая теорема двойственности - доказательство пункта б и г (слайд 1).
 2. Первая теорема двойственности - доказательство пункта б и г (слайд 1).
2. Первая теорема двойственности - доказательство пункта б и г (слайд 1).
 3. Вторая теорема двойственности (слайд 1).
3. Вторая теорема двойственности (слайд 1).
 3. Вторая теорема двойственности (слайд 2).
3. Вторая теорема двойственности (слайд 2).
 3. Вторая теорема двойственности (слайд 3).
3. Вторая теорема двойственности (слайд 3).
 4. Получение оптимального решения двойственной задачи по решению прямой.
4. Получение оптимального решения двойственной задачи по решению прямой.
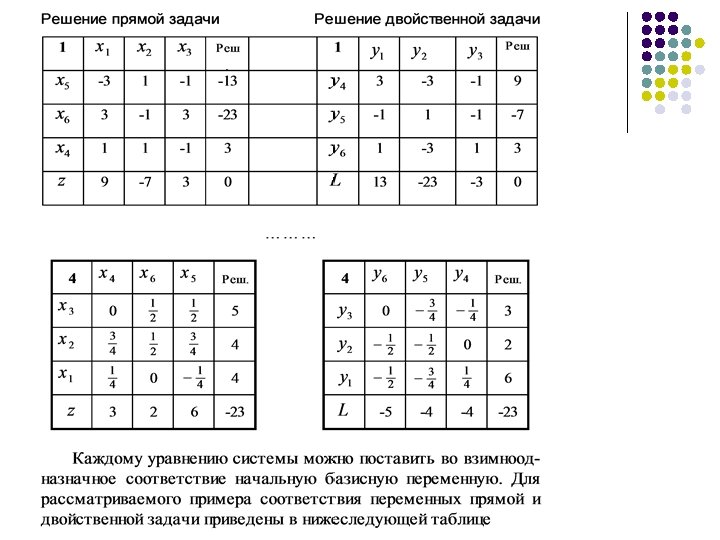
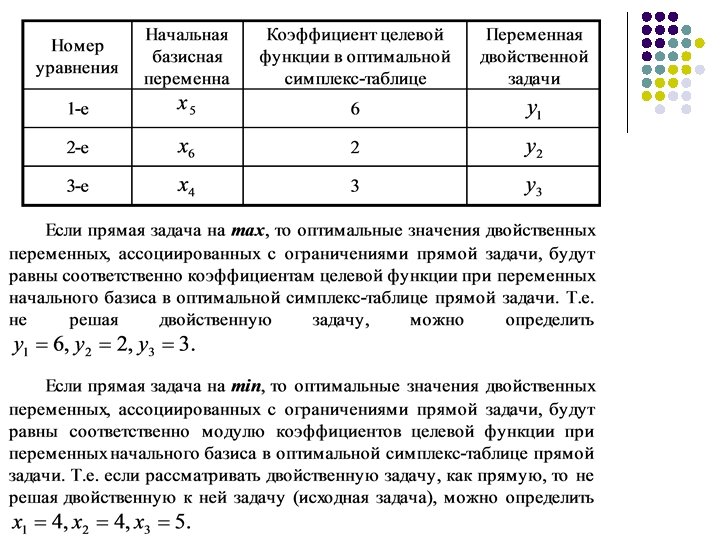
 4. Получение оптимального решения двойственной задачи по решению прямой.
4. Получение оптимального решения двойственной задачи по решению прямой.
 5. Двойственный симплекс-метод. Двойственный симплекс метод это такой алгоритм решения исходной задачи, для которого на каждой итерации, за исключением последней, решение оказывается недопустимым вследствие невыполнения условия не отрицательности переменных; соответствующее же решение двойственной задачи при каждой такой итерации является допустимым. Такой алгоритм позволяет в ряде случаев облегчить поиск оптимального решения без определения начального опорного решения. В тоже время этот алгоритм позволяет произвести некоторые виды анализа моделей на чувствительность. Рассмотрим пример:
5. Двойственный симплекс-метод. Двойственный симплекс метод это такой алгоритм решения исходной задачи, для которого на каждой итерации, за исключением последней, решение оказывается недопустимым вследствие невыполнения условия не отрицательности переменных; соответствующее же решение двойственной задачи при каждой такой итерации является допустимым. Такой алгоритм позволяет в ряде случаев облегчить поиск оптимального решения без определения начального опорного решения. В тоже время этот алгоритм позволяет произвести некоторые виды анализа моделей на чувствительность. Рассмотрим пример:

 Алгоритм двойственного симплекс-метода
Алгоритм двойственного симплекс-метода

 Лекция 10 Тема: Целочисленное программирование Рассматриваются вопросы: 1. Примеры постановок задачи целочисленного программирования. 2. Некоторые задачи нелинейного программирования, которые сводятся к задаче целочисленного программирования 2. 1. задачи с постоянным элементом затрат; 2. 2. задачи на разрывных областях; 2. 3. задачи с дихотомией.
Лекция 10 Тема: Целочисленное программирование Рассматриваются вопросы: 1. Примеры постановок задачи целочисленного программирования. 2. Некоторые задачи нелинейного программирования, которые сводятся к задаче целочисленного программирования 2. 1. задачи с постоянным элементом затрат; 2. 2. задачи на разрывных областях; 2. 3. задачи с дихотомией.
 1. Примеры постановок задачи целочисленного программирования. l Задача называется полностью целочисленной, если условие целочисленности наложено на все ее переменные, если условие целочисленности распространяется не на все переменные, то задача называется частично целочисленной. l Как правило, в задачах целочисленного программирования нельзя получить хороших приближений простым округлением решений задачи, полученных при снятии условия целочисленности. l Особое место среди целочисленных задач имеют задачи c булевыми переменными, для таких задач округление вообще не имеет смысла.
1. Примеры постановок задачи целочисленного программирования. l Задача называется полностью целочисленной, если условие целочисленности наложено на все ее переменные, если условие целочисленности распространяется не на все переменные, то задача называется частично целочисленной. l Как правило, в задачах целочисленного программирования нельзя получить хороших приближений простым округлением решений задачи, полученных при снятии условия целочисленности. l Особое место среди целочисленных задач имеют задачи c булевыми переменными, для таких задач округление вообще не имеет смысла.
 1. Примеры постановок задачи целочисленного программирования. Задача о ранце
1. Примеры постановок задачи целочисленного программирования. Задача о ранце
 1. Примеры постановок задачи целочисленного программирования. Задача закрепления рабочей силы
1. Примеры постановок задачи целочисленного программирования. Задача закрепления рабочей силы
 2. 1. Задача c постоянным элементом затрат (слайд 1).
2. 1. Задача c постоянным элементом затрат (слайд 1).
 2. 1. Задача c постоянным элементом затрат (слайд 2).
2. 1. Задача c постоянным элементом затрат (слайд 2).
 2. 2. Задача c ограничением на размер партии.
2. 2. Задача c ограничением на размер партии.
 2. 3. Задача c дихотомией.
2. 3. Задача c дихотомией.
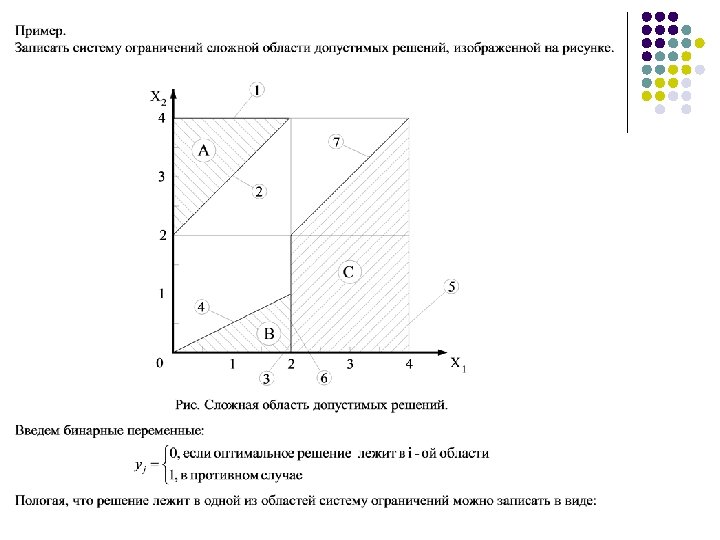
 Система ограничений для примера с разрывными областями
Система ограничений для примера с разрывными областями
 Лекция 11 Тема: Целочисленное программирование Рассматриваются вопросы: 1. Метод отсекающей плоскости. 2. Метод ветвей и границ.
Лекция 11 Тема: Целочисленное программирование Рассматриваются вопросы: 1. Метод отсекающей плоскости. 2. Метод ветвей и границ.
 1. Метод отсекающих плоскостей
1. Метод отсекающих плоскостей
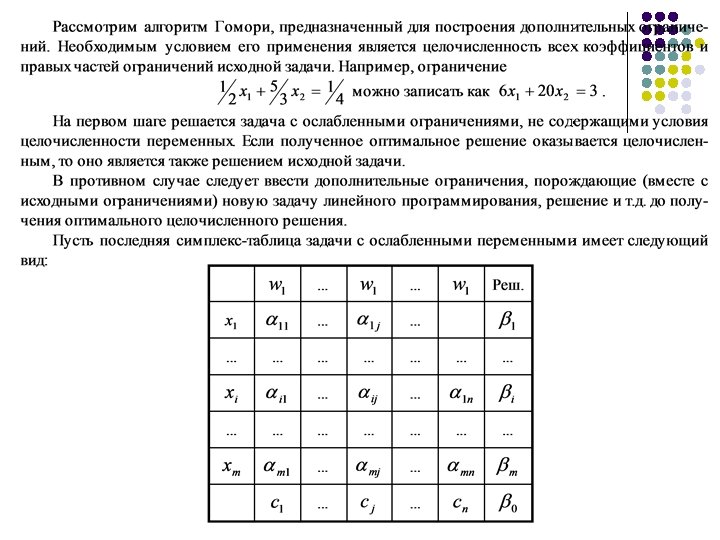

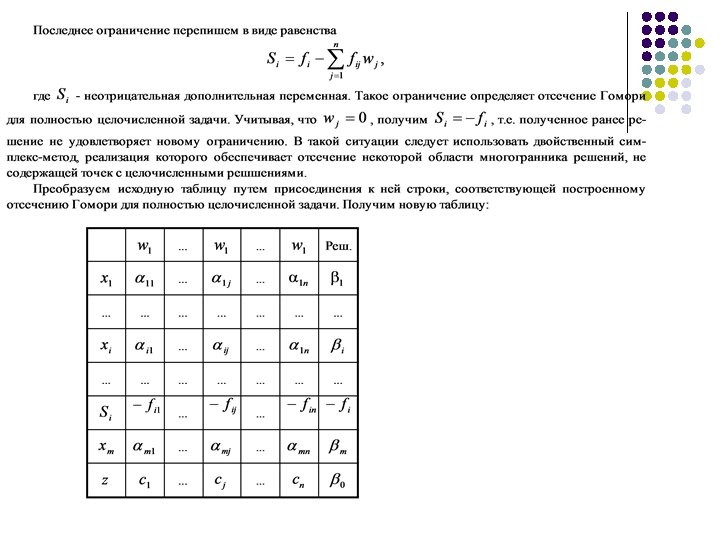
 1. Метод отсекающих плоскостей l Еcли полученное решение (в результате применения двойственного cимплекc метода) является целочисленным, то процесс решения задачи завершен. В противном случае необходимо ввести новое отсечение на базе полученной таблицы и вновь воспользоваться двойственным симплекс методом. Процедура повторяется до тех пор, пока не будет найдено целочисленное решение. Еcли на некоторой итерации при использовании двойственного cимплекc метода обнаружено отсутствие допустимого решения, то исходная задача не имеет целочисленного решения. l Рассмотренный алгоритм иначе называется дробным, поскольку все ненулевые коэффициенты вводимых ограничений меньше либо равны единицы. После небольших изменений этот алгоритм применим и к частично целочисленным задачам.
1. Метод отсекающих плоскостей l Еcли полученное решение (в результате применения двойственного cимплекc метода) является целочисленным, то процесс решения задачи завершен. В противном случае необходимо ввести новое отсечение на базе полученной таблицы и вновь воспользоваться двойственным симплекс методом. Процедура повторяется до тех пор, пока не будет найдено целочисленное решение. Еcли на некоторой итерации при использовании двойственного cимплекc метода обнаружено отсутствие допустимого решения, то исходная задача не имеет целочисленного решения. l Рассмотренный алгоритм иначе называется дробным, поскольку все ненулевые коэффициенты вводимых ограничений меньше либо равны единицы. После небольших изменений этот алгоритм применим и к частично целочисленным задачам.
 2. 1. Метод ветвей и границ.
2. 1. Метод ветвей и границ.
 Лекция 12 Тема: Элементы теории игр Рассматриваются вопросы: 1. Основные понятия теории игр 2. Платежная матрица. 3. Примеры простейших игр. 4. Нижняя и верхняя цена игры. 5. Решение игры в смешанных стратегиях. 6. Упрощение игр.
Лекция 12 Тема: Элементы теории игр Рассматриваются вопросы: 1. Основные понятия теории игр 2. Платежная матрица. 3. Примеры простейших игр. 4. Нижняя и верхняя цена игры. 5. Решение игры в смешанных стратегиях. 6. Упрощение игр.
 1. Основные понятия теории игр (слайд 1).
1. Основные понятия теории игр (слайд 1).
 1. Основные понятия теории игр (слайд 2).
1. Основные понятия теории игр (слайд 2).
 1. Основные понятия теории игр (слайд 3).
1. Основные понятия теории игр (слайд 3).
 1. Основные понятия теории игр (слайд 4).
1. Основные понятия теории игр (слайд 4).
 2. Платежная матрица игры (слайд 1).
2. Платежная матрица игры (слайд 1).
 2. Платежная матрица игры (слайд 2).
2. Платежная матрица игры (слайд 2).
 3. Примеры простейших игр (слайд 1).
3. Примеры простейших игр (слайд 1).
 3. Примеры простейших игр (слайд 2).
3. Примеры простейших игр (слайд 2).
 4. Нижняя и верхняя цена игры (слайд 1).
4. Нижняя и верхняя цена игры (слайд 1).
 4. Нижняя и верхняя цена игры (слайд 2).
4. Нижняя и верхняя цена игры (слайд 2).
 4. Нижняя и верхняя цена игры (слайд 3).
4. Нижняя и верхняя цена игры (слайд 3).
 5. Решение игр в смешанных стратегиях (слайд 1).
5. Решение игр в смешанных стратегиях (слайд 1).
 5. Решение игр в смешанных стратегиях (слайд 2).
5. Решение игр в смешанных стратегиях (слайд 2).
 5. Решение игр в смешанных стратегиях (слайд 3).
5. Решение игр в смешанных стратегиях (слайд 3).
 6. Упрощение игр (слайд 1).
6. Упрощение игр (слайд 1).
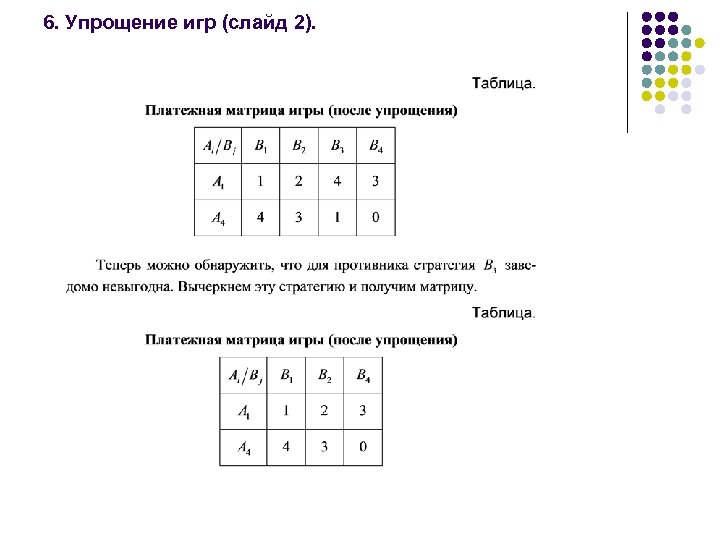 6. Упрощение игр (слайд 2).
6. Упрощение игр (слайд 2).
 6. Упрощение игр (слайд 3).
6. Упрощение игр (слайд 3).
 6. Упрощение игр (слайд 4).
6. Упрощение игр (слайд 4).
 Лекция 13 Тема: Элементы теории игр Рассматриваются вопросы: 1. Геометрическая интерпретация игры 2*2. 2. Решение игр 2*n и m*2. 3. Приведение матричной игры к задаче линейного программирования.
Лекция 13 Тема: Элементы теории игр Рассматриваются вопросы: 1. Геометрическая интерпретация игры 2*2. 2. Решение игр 2*n и m*2. 3. Приведение матричной игры к задаче линейного программирования.
 1. Геометрическая интерпретация игры 2*2 (слайд 1).
1. Геометрическая интерпретация игры 2*2 (слайд 1).
 1. Геометрическая интерпретация игры 2*2 (слайд 2).
1. Геометрическая интерпретация игры 2*2 (слайд 2).
 1. Геометрическая интерпретация игры 2*2 (слайд 3).
1. Геометрическая интерпретация игры 2*2 (слайд 3).
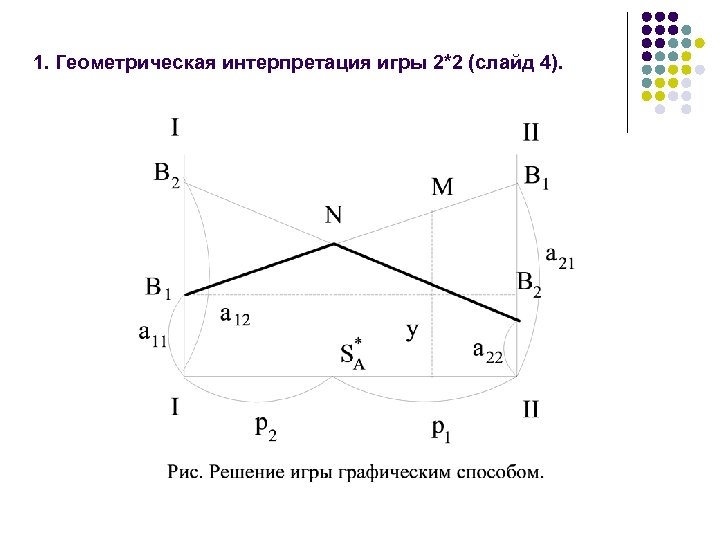 1. Геометрическая интерпретация игры 2*2 (слайд 4).
1. Геометрическая интерпретация игры 2*2 (слайд 4).
 2. Решение игр 2*n и m*2.
2. Решение игр 2*n и m*2.
 3. Приведение матричной игры к задаче линейного программирования (слайд 1).
3. Приведение матричной игры к задаче линейного программирования (слайд 1).
 3. Приведение матричной игры к задаче линейного программирования (слайд 2).
3. Приведение матричной игры к задаче линейного программирования (слайд 2).
 3. Приведение матричной игры к задаче линейного программирования (слайд 3).
3. Приведение матричной игры к задаче линейного программирования (слайд 3).
 3. Приведение матричной игры к задаче линейного программирования (слайд 4).
3. Приведение матричной игры к задаче линейного программирования (слайд 4).
 3. Приведение матричной игры к задаче линейного программирования (слайд 5).
3. Приведение матричной игры к задаче линейного программирования (слайд 5).
 Лекция 14 Тема: Модели сетевого планирования и управления Рассматриваются вопросы: 1. Основные элементы сетевой модели. 2. Расчет параметров сетевого графика. 3. График Ганта. Оптимизация сетевого графика методом «времястоимость» .
Лекция 14 Тема: Модели сетевого планирования и управления Рассматриваются вопросы: 1. Основные элементы сетевой модели. 2. Расчет параметров сетевого графика. 3. График Ганта. Оптимизация сетевого графика методом «времястоимость» .
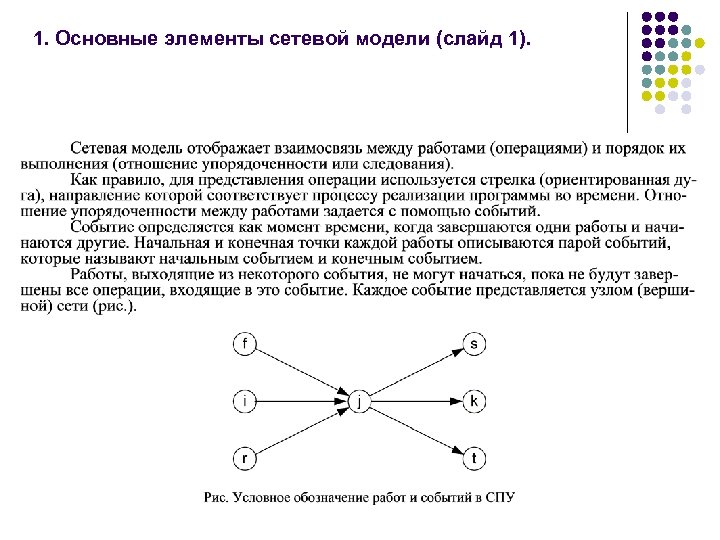 1. Основные элементы сетевой модели (слайд 1).
1. Основные элементы сетевой модели (слайд 1).
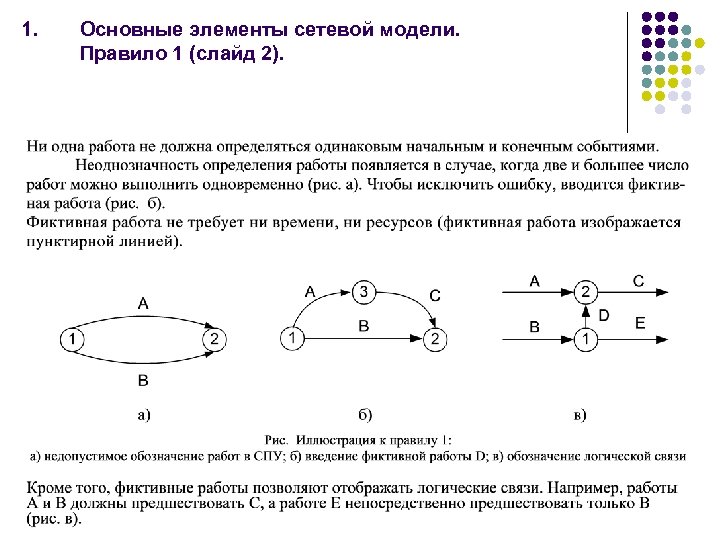 1. Основные элементы сетевой модели. Правило 1 (слайд 2).
1. Основные элементы сетевой модели. Правило 1 (слайд 2).
 1. Основные элементы сетевой модели. Правило 2 (слайд 3).
1. Основные элементы сетевой модели. Правило 2 (слайд 3).
 2. Расчет параметров сетевого графика. (слайд 1).
2. Расчет параметров сетевого графика. (слайд 1).
 2. Расчет параметров сетевого графика. (слайд 2).
2. Расчет параметров сетевого графика. (слайд 2).
 2. Расчет параметров сетевого графика. (слайд 3).
2. Расчет параметров сетевого графика. (слайд 3).
 2. Расчет параметров сетевого графика (слайд 4).
2. Расчет параметров сетевого графика (слайд 4).
 2. Расчет параметров сетевого графика (слайд 5).
2. Расчет параметров сетевого графика (слайд 5).
 2. Расчет параметров сетевого графика (слайд 5).
2. Расчет параметров сетевого графика (слайд 5).
 2. Расчет параметров сетевого графика (слайд 6).
2. Расчет параметров сетевого графика (слайд 6).
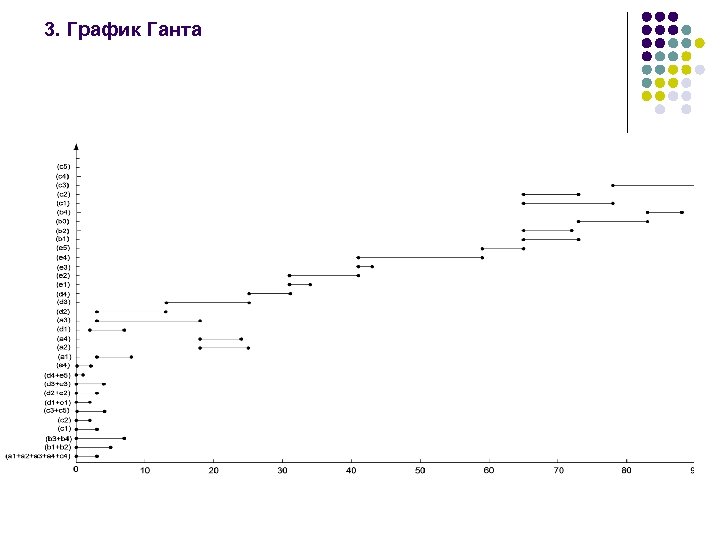 3. График Ганта
3. График Ганта
 Лекция 15 Тема: Модели динамического программирования Рассматриваются вопросы: 1. 2. 3. 4. Общая постановка задачи динамического программирования. Принцип Беллмана. Задача о наборе высоты и скорости летательного аппарата. Задача распределения средств между предприятиями.
Лекция 15 Тема: Модели динамического программирования Рассматриваются вопросы: 1. 2. 3. 4. Общая постановка задачи динамического программирования. Принцип Беллмана. Задача о наборе высоты и скорости летательного аппарата. Задача распределения средств между предприятиями.
 1. Общая постановка задачи динамического программирования. Динамическое программирование – метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Такие операции называются многошаговыми.
1. Общая постановка задачи динамического программирования. Динамическое программирование – метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Такие операции называются многошаговыми.
 2. Принцип оптимальности Беллмана.
2. Принцип оптимальности Беллмана.
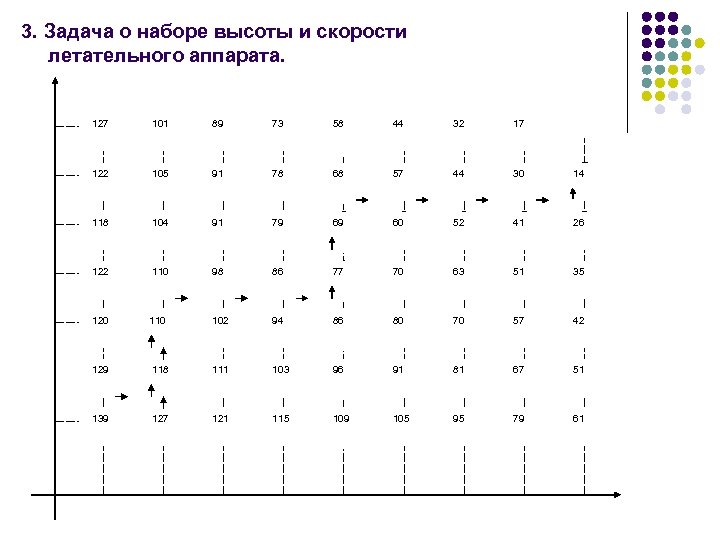 3. Задача о наборе высоты и скорости летательного аппарата. 127 101 89 73 44 58 32 17 122 17 105 14 91 13 78 10 68 11 57 13 44 14 30 17 14 118 14 104 13 91 12 79 10 69 9 60 8 52 11 41 15 26 122 110 98 86 77 70 63 51 35 120 10 110 8 102 8 94 8 86 10 80 12 70 13 57 15 42 129 11 118 9 111 8 103 7 96 9 91 13 81 14 67 18 51 139 12 127 11 121 10 115 9 109 13 105 14 95 17 79 20 61
3. Задача о наборе высоты и скорости летательного аппарата. 127 101 89 73 44 58 32 17 122 17 105 14 91 13 78 10 68 11 57 13 44 14 30 17 14 118 14 104 13 91 12 79 10 69 9 60 8 52 11 41 15 26 122 110 98 86 77 70 63 51 35 120 10 110 8 102 8 94 8 86 10 80 12 70 13 57 15 42 129 11 118 9 111 8 103 7 96 9 91 13 81 14 67 18 51 139 12 127 11 121 10 115 9 109 13 105 14 95 17 79 20 61
 4. Задача распределения средств между предприятиями.
4. Задача распределения средств между предприятиями.
 Лекция 16 Тема: Разработка и анализ оптимизационных моделей по содержательной постановке на ПЭВМ. Рассматриваются вопросы: 1. Решение задачи линейного программирования с помощью программы поиск решения EXCEL.
Лекция 16 Тема: Разработка и анализ оптимизационных моделей по содержательной постановке на ПЭВМ. Рассматриваются вопросы: 1. Решение задачи линейного программирования с помощью программы поиск решения EXCEL.
 1. Постановка задачи.
1. Постановка задачи.
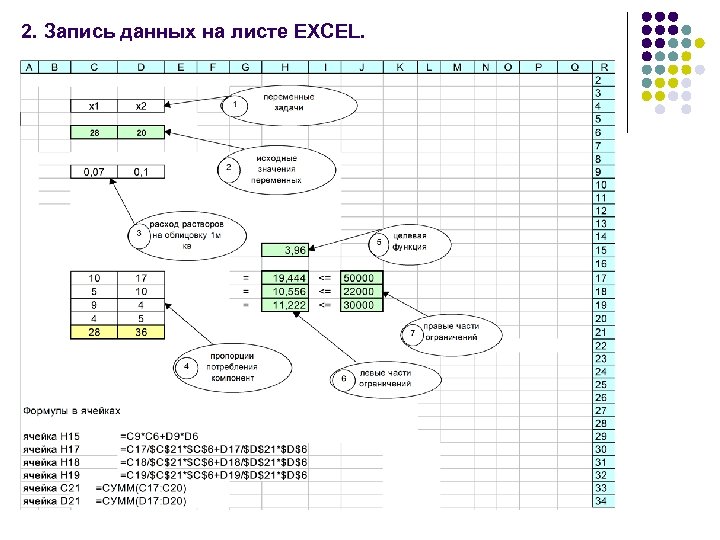 2. Запись данных на листе EXCEL.
2. Запись данных на листе EXCEL.
 3. Главное окно программы “поиск решений.
3. Главное окно программы “поиск решений.
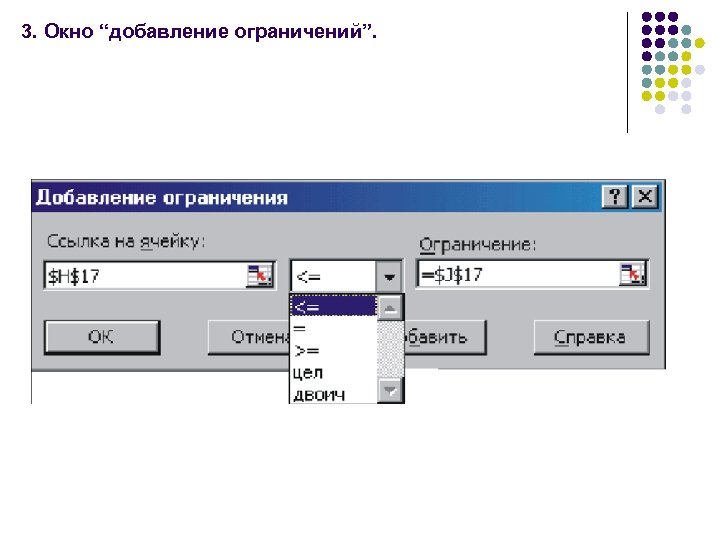 3. Окно “добавление ограничений”.
3. Окно “добавление ограничений”.
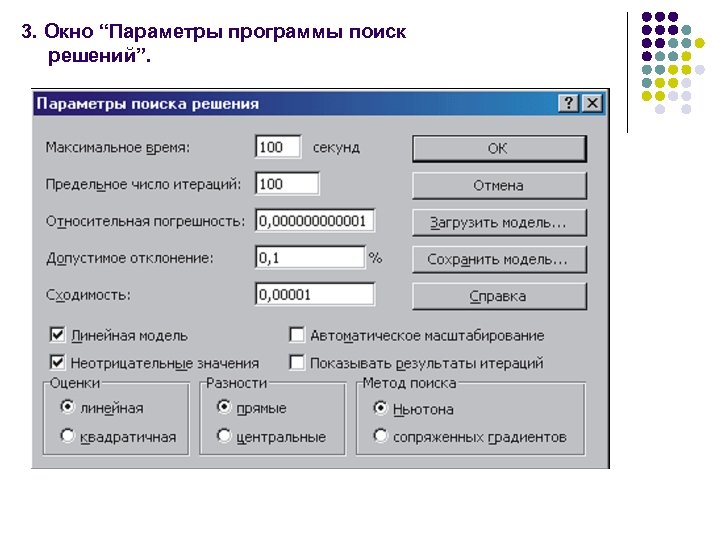 3. Окно “Параметры программы поиск решений”.
3. Окно “Параметры программы поиск решений”.
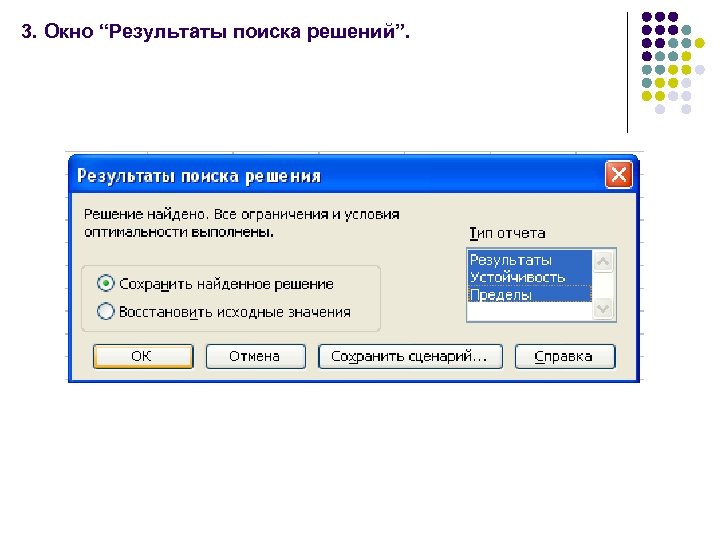 3. Окно “Результаты поиска решений”.
3. Окно “Результаты поиска решений”.
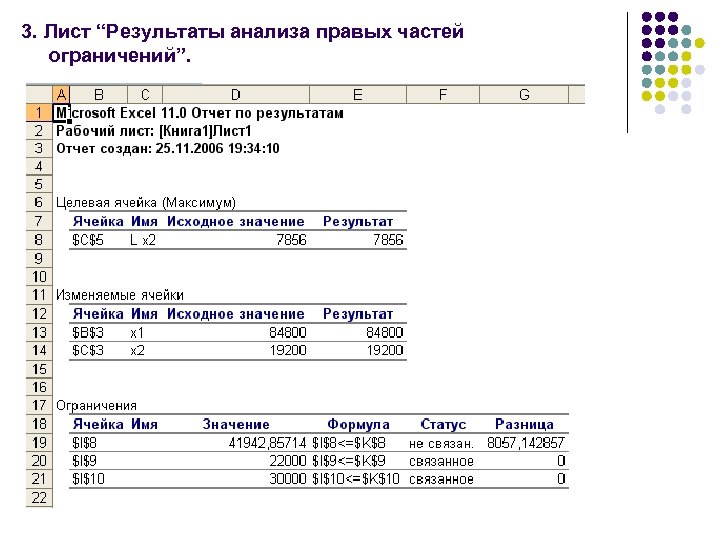 3. Лист “Результаты анализа правых частей ограничений”.
3. Лист “Результаты анализа правых частей ограничений”.
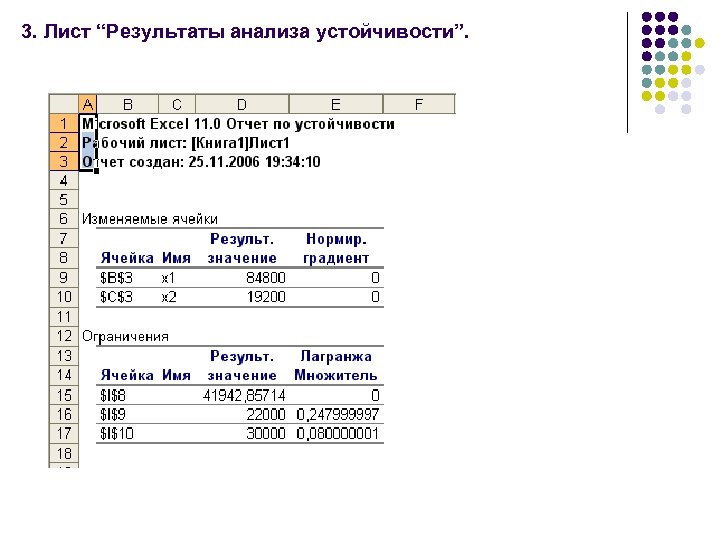 3. Лист “Результаты анализа устойчивости”.
3. Лист “Результаты анализа устойчивости”.
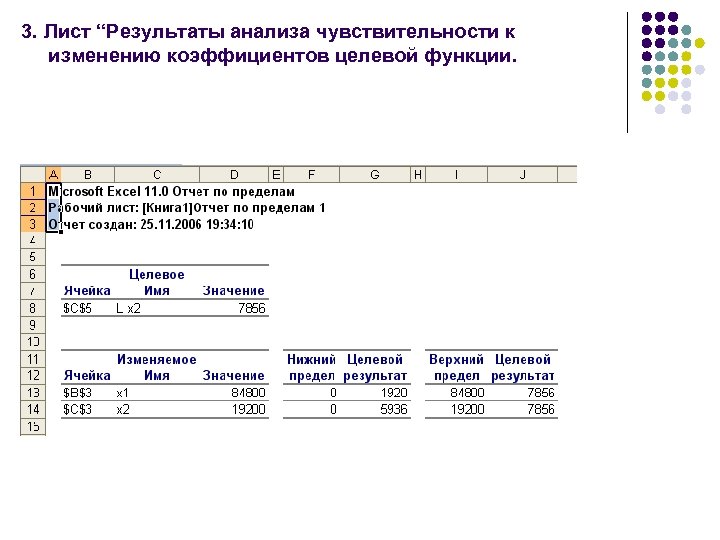 3. Лист “Результаты анализа чувствительности к изменению коэффициентов целевой функции.
3. Лист “Результаты анализа чувствительности к изменению коэффициентов целевой функции.


