Исследование операций Курс Исследование операций ИСО рассчитан на

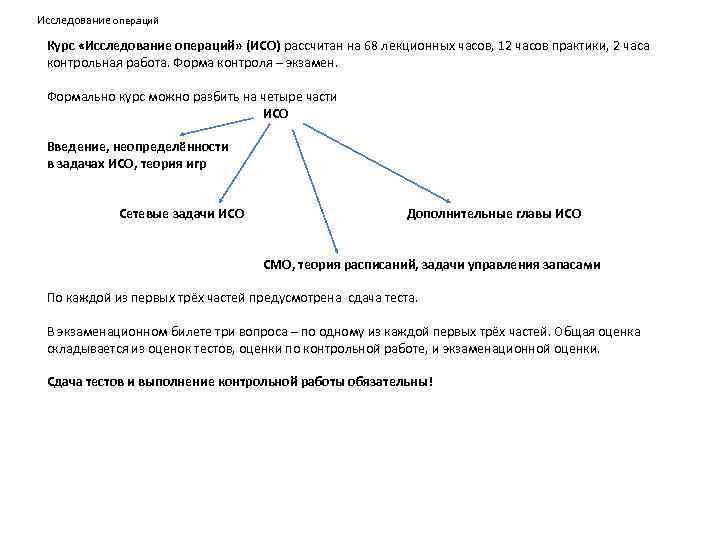Исследование операций Курс «Исследование операций» (ИСО) рассчитан на 68 лекционных часов, 12 часов практики, 2 часа контрольная работа. Форма контроля – экзамен. Формально курс можно разбить на четыре части ИСО Введение, неопределённости в задачах ИСО, теория игр Сетевые задачи ИСО Дополнительные главы ИСО СМО, теория расписаний, задачи управления запасами По каждой из первых трёх частей предусмотрена сдача теста. В экзаменационном билете три вопроса – по одному из каждой первых трёх частей. Общая оценка складывается из оценок тестов, оценки по контрольной работе, и экзаменационной оценки. Сдача тестов и выполнение контрольной работы обязательны!

Исследование операций Литература рекомендуемая для изучения курса: • Гермейер Ю. Б. Введение в теорию исследования операций. – М. : Наука, 1971. – 383 с. • Вагнер Г. Основы исследования операций. – М. : Мир, 1972 (в трёх томах). • Танаев В. С. , Шкурба В. В. Введение в теорию расписаний. – М. : Наука, 1975. – 256 с. • Крушевский А. В. Теория игр. – Киев: Выща школа, 1977. – 216 с. (Изложены основные положения и сведения из теории игр). • Фрэнк Г. , Фриш И. Сети, связь и потоки. – М. : Связь, 1978. – 448 с. • Сакович В. А. Исследование операций. – Мн. : Выш. шк. , 1984. – 256 с. (Излагатся количественные методы анализа и синтеза оптимальных решений). • Свами М. , Тхуласираман К. Графы, сети и алгоритмы. – М. : Мир, 1984. – 455 с. • Морозов В. В. , Сухарев А. Г. , Фёдоров В. В. Исследование операций в задачах и упражнениях. – М. : Высш. шк. , 1986. – 287 с. (Знакомит с основными понятиями и методами исследования операций). • Вентцель Е. С. Исследование операций. Задачи, принципы, методология. –М. : Наука. 1988. – 208 с. (Популярно излагаются основы ИСО. Главное внимание уделяется не математическому аппарату, а методологии). • Танаев В. С. , Сотсков Ю. Н. , Струсевич В. А. Теория расписаний. Многостадийные системы. – М. : Наука, 1989. – 328 с. • Давыдов Э. Г. Исследование операций. – М. : Высш. шк. , 1990. – 383 с. (Излагаются методологические основы исследования операций). • Петросян Л. А. , Зенкевич Н. А. , Сёмина Е. А. Теория игр. – М. : Высш. шк. , 1998. - 304 с. (Краткое учебное пособие по теории игр). • Бахтин В. И. и др. Исследование операций: Курс лекций. – Минск: БГУ, 2003. – 199 с. • Таха Х. Введение в исследование операций (7 - изд. ). – Вильямс, 2005. – 903 с. • Костевич Л. С. , Лако А. А. Исследование операций. Теория игр (2 -изд. ). - Минск: Выш. шк. , 2008. – 368 с.

Исследование операций Литература рекомендуемая для изучения курса: • Исаченко А. Н. , Дробушевич Л. Ф. Исследование операций в задачах. В 3 ч. , Ч. 1: Математические модели. Теория игр. – Минск: БГУ, 2010. – 50 с. • Исаченко А. Н. , Дробушевич Л. Ф. Исследование операций в задачах. В 3 ч. , Ч. 2: Сетевые задачи. – Минск: БГУ, 2011. – 76 с.

Исследование операций Под операциями обычно понимают целенаправленные управляемые процессы. Природа их может быть различной - это могут быть военные действия, производственные процессы, коммерческие мероприятия, административные решения и т. д. История возникновения исследования операций. 1) В 1885 году Фредерик Тейлор пришел к выводу о возможности применения научного анализа в сфере производства. Проблема, рассмотренная им, на первый взгляд, кажется тривиальной: "как оптимальным образом организовать работу землекопов? " Казалось бы, ответ давно известен - "Бери больше, кидай дальше, отдыхай, пока летит". Однако применение математического аппарата показало несостоятельность этого принципа. Оказалось, что оптимальный вес груза, позволяющий максимизировать количество перебрасываемого материала (при разумной экономии рабочей силы) значительно меньше того, что может поднять человек при максимальной нагрузке. 2) Пионером в области перевода сложных военно-стратегических задач на язык математики стал Фредерик Ланчестер. Одним из наиболее значительных результатов, полученных ученым, стало открытие в 1916 г. так называемого квадратичного закона, количественно связывающего достижение победы с двумя основными факторами: численным превосходством живой силы и эффективностью оружия. Было показано, что при одновременном вступлении в бой численное превосходство в живой силе более важно, чем применение более совершенного вооружения, поскольку главную роль играет сосредоточение собственных войск и расчленение сил противника. 3) В 1917 году датский математик А. К. Эрланг, работавший в телефонной компании, поставил задачу минимизации потерь времени на установление телефонной связи. Полученные им результаты стали основополагающими принципами в теории телефонной связи. Формулы Эрланга (среднее время ожидания вызова и др. ) были приняты министерством связи Англии в качестве стандартов для расчета эффективности телефонных линий. Идеи Эрланга почти на полвека предвосхитили современные теории расчета телефонных узлов.

Исследование операций 4) В 1930 г. Г. Левинсон начал применять научный анализ к решению задач, возникающих в торговле. Методика исследования операций была использована для исследования эффективности рекламы, размещения товаров, влияния конъюнктуры на номенклатуру и количество проданных товаров. 5) В 1935 г. в Великобритании с целью подготовки эффективных средств противодействия возрастающей угрозе со стороны военно-воздушных сил Германии ученые начали форсированную подготовку серии экспериментов, направленных на разработку системы обнаружения самолетов, основанной на радиолокации. По мере того как новые тактические операции отрабатывались в рамках крупномасштабных учебных действий в воздухе, ученые стали уделять все большее внимание оценке эффективности разрабатываемых операций. Применительно как раз к таким исследованиям в 1938 г. впервые использовали термин "операционное исследование» . Период с 1935 по 1938 г. - время формирования основных положений научного направления ИСО. В годы второй мировой войны исследование операций широко применялось для планирования боевых действий. Так, специалисты по исследованию операций работали в командовании бомбардировочной авиации США, дислоцированном в Англии. Ими исследовались многочисленные факторы, влияющие на эффективность бомбометания. Были выработаны рекомендации, приведшие к 4 -х-кратному повышению эффективности бомбометания. Общее число ученых в Англии, Америке и Канаде привлечённых к операционным исследованиям вов время 2 -ой мировой войны превышало 700 человек. Отделы ИСО были созданы в основных командных органах вооружённых сил Великобритании, США, Канады. Среди организаторов исследований два лауреата Нобелевской премии: П. Блеккет, физик, получивший впоследствии за свои работы по исследованию космических лучей Нобелевскую премию, У. Шокли , ставшей лауреатом Нобелевской премии за работы по транзисторам.

Исследование операций Предмет ИСО В широком смысле ИСО – есть научный подход к решению задач организационного управления или научное обоснование задач принятия решений. Сложность задач организационного управления обусловлена следующими причинами: 1) в организационных системах достаточно трудно определить и предусмотреть какие-либо случайные состояния; 2) практически невозможно провести предварительный эксперимент по поведению организационных систем; 3) при управлении, как правило, имеется много взаимосвязанных между собой факторов, влияющих на возможные варианты решений. 4) помимо этого в любой организационной задаче всегда фигурируют "человеческий фактор", который с трудом поддается изучению и количественному анализу.

Исследование операций Предмет ИСО – прикладная математическая дисциплина, которая занимается вопросами количественного обоснования решений по управлению целенаправленными процессами (операциями) в сложных системах. В данном определении принципиально важными являются три ключевых момента. 1) Объектом исследования является система. Система – это совокупность объектов, связанных взаимными отношениями, и рассматриваемая как единое целое. Система взаимодействует с внешней средой. Предметом изучения является решение в сложных системах. 2) Исследуются целенаправленные процессы. Понятие цели является центральным, определяющим при исследовании сложных систем. . По отношению к анализируемой операции всегда выделяется субъект, который преследует вполне определенную цель и стремится достичь ее с помощью своих решений. Понятие операции также связано с целью. Операция это любая целенаправленная совокупность действий. 3) Использование математических методов исследования. Подчеркивая использование математических методов, ИСО можно определить как построение, разработку и приложение математических моделей принятия оптимальных решений.

Исследование операций Методология операционного исследования Каждое операционное исследование содержит несколько типовых этапов: 1) Постановка задачи и разработка концептуальной модели. 2) Построение математической модели. 3) Выбор метода и алгоритма решения. 4) Проверка адекватности и корректировка модели. 5) Поиск решения на математической модели. 6) Реализация найденного решения на практике.

Исследование операций 1) Методология операционного исследования Постановка задачи и разработка концептуальной модели. Первоначально задачу операционного исследования формулирует субъект, в чьих интересах проводится операционное исследование. Как правило, постановка задачи имеет общий характер. Для проведения исследований создается операционная группа из системных аналитиков, специалистов предметной области, к которой относится система, социологов, психологов и т. п. Операционная группа выделяет исследуемый объект или явление из среды, детально обследует соответствующую систему, изучает информационные и материальные потоки в самой системе, её связи с внешней средой. Одновременно изучаются организация подсистемы управления данной системой, а также показатели качества или критерии эффективности функционирования системы и внешние факторы, которые влияют на эти характеристики. После сбора результатов обследования проводится их подробный анализ, в результате которого обнаруживаются существенные факторы и переменные, обосновывается выбор тех или иных показателей качества функционирования системы, а также существенных внешних факторов, структура самой системы, состав его элементов, их взаимосвязи, внутренние параметры. По возможности определяются структурные категории системы (стохастичность, детерминированность, статичность, динамичность, линейность, нелинейность). Результатом этого этапа является концептуальная модель исследуемой системы (задачи). В ней в содержательной форме описывается состав системы, её компоненты и их взаимосвязи, контролируемые и неконтролируемых внешние факторы, перечень основных показателей функционирования системы, перечень стратегий управления (или решений), которые надо определить в результате решения поставленной задачи.

Методология операционного исследования Исследование операций 2) Построение математической модели. Существует два подхода к построению математической модели: идентификация и планирование эксперимента. В первом случае модель строится в режиме пассивного наблюдения над системой без оказания на неё каких-либо воздействий. При планировании эксперимента организуются серия управляющие воздействия на систему, которая называется планом эксперимента, с целью наиболее достоверного выявления структурных категорий и зависимостей между входными и выходными параметрами модели. X={xi} A={ak} Y={yj} ={ p} Состояние системы Y зависит от X, A, и математическая модель должна с определённой точностью отражать эту зависимость Y=f(X, A, ). В общем случае математическая модель системы примет вид Y=f(X, A, ), при ограничениях gi(X, A, ) bi, i=1, …, m, Xmin X Xmax, Ymin Y Ymax, где gi(X, A, )- функция затрат i-го ресурса, bi – величина i-го ресурса в системе.

Исследование операций Методология операционного исследования После того как математическая модель системы построена, необходимо указать цель операции, которая выражается функцией предпочтения на множестве состояний системы F(Y). Целевая функция F(Y) - критерий эффективности, который зависит от принятых стратегий, параметров системы и возмущений. Таким образом, математическая модель примет вид F(Y) max(min) X при выполнении условий gi(X, A, ) bi, i=1, …, m, Xmin X Xmax, Ymin Y Ymax, При построении математической модели существенную роль может сыграть декомпозиция системы на составляющие, связанные между собой элементы, которые проще исходной системы.

Исследование операций Методология операционного исследования 3) Выбор метода и алгоритма решения. Для нахождения оптимального решения задачи в зависимости от вида и структуры целевой функции и ограничений используют те или другие методы теории оптимальных решений. Линейное программирование. Нелинейное программирование. Дискретное программирование. Динамическое программирование, если функции f(X) и gi(X) имеют специальную структуру и являются аддитивными или мультипликативными от переменных X. f(x 1, …, xn) - аддитивная функция, если f(x 1, …, xn)= и - мультипликативная, если f(x 1, …, xn)= Геометрическое программирование, если функция f(X) и ограничения gi(X) представляют собой так называемые функции - позиномы: Стохастическое программирование, если вектор внешних переменных ={ s} или (и) параметров системы A={ak} нерегулируемый и случайный. В этом случае математическая модель будет иметь вид минимизировать M (X, Y, A, ) при ограничениях M {gi(X, A, )} bi, i=1, …, m, или случайных ограничениях P{ gi(X, A, ) bi } 1 - , i=1, …, m, где M математическое ожидание по переменным , P{gi(X, A, ) bi } - соответствующая вероятность того, что выполняется условие gi(X, A, ) bi. Нечеткое математическое программирование, когда приходится принимать решение в условиях неопределенности. Комбинаторное и эвристическое программирование. Его применяют для решения тех задач, в которых задача имеет комбинаторный характера и связана с ним огромного количества вариантов.

Исследование операций Методология операционного исследования 4) Проверка адекватности и корректировка модели. В сложных системах модель лишь частично отражает реальный объект (или процесс). Поэтому необходимо проводить проверку степени соответствия (или адекватности) модели и реального процесса. Проверку можно проводить путем сравнения выходных характеристик модели YM или предвиденного поведения модели с фактическими характеристиками объекта YO при изменении значений управляющих X и внешних факторов , а также (при возможности) параметров системы A в широком диапазоне колебаний. В качестве меры адекватности модели выбирают некоторую меру близости YM и YO, например, одну из следующих величин: а) абсолютное отклонение a=| YM –YO | доп ; б) относительное отклонение ; в) вероятностная оценка . Возможны корректировки концептуальной модели, математической модели и соответственно метода решения.

Исследование операций Методология операционного исследования 5) Поиск решения на модели. После достижения удовлетворительного уровня адекватности модели применяют соответствующий метод или алгоритм для нахождения оптимального (или субоптимального) решения на математической модели. Это решение может принимать разные формы: аналитическую, численную, или алгоритмическую (в виде набора процедур, правил, и т. п. ). 6) Реализация найденного решения на практике. Внедрение в практику найденного на модели решения можно рассмотреть как самостоятельную задачу. Полученной на модели оптимальной стратегии управления необходимо предоставить соответствующую содержательную форму в виде инструкций и правил, что и как делать, которая была бы понятной для административного персонала данной организации и легкой для выполнения в производственных условиях.

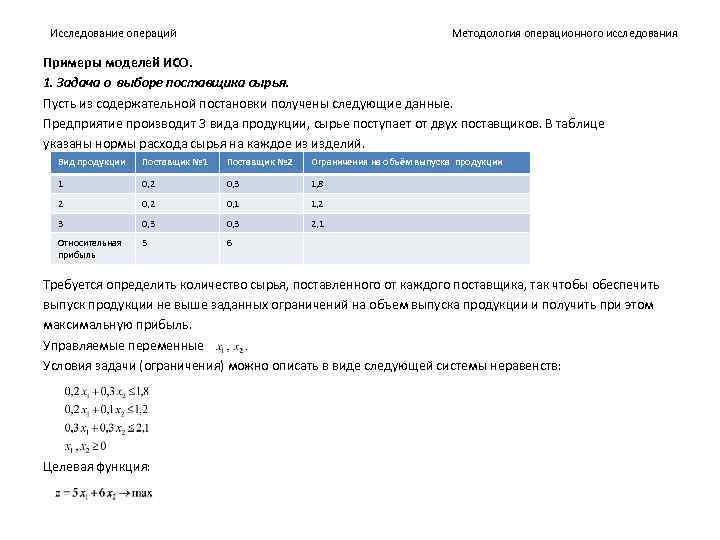Методология операционного исследования Исследование операций Примеры моделей ИСО. 1. Задача о выборе поставщика сырья. Пусть из содержательной постановки получены следующие данные. Предприятие производит 3 вида продукции, сырье поступает от двух поставщиков. В таблице указаны нормы расхода сырья на каждое из изделий. Вид продукции Поставщик № 1 Поставщик № 2 Ограничения на объём выпуска продукции 1 0, 2 0, 3 1, 8 2 0, 1 1, 2 3 0, 3 2, 1 Относительная прибыль 5 6 Требуется определить количество сырья, поставленного от каждого поставщика, так чтобы обеспечить выпуск продукции не выше заданных ограничений на объем выпуска продукции и получить при этом максимальную прибыль. Управляемые переменные Условия задачи (ограничения) можно описать в виде следующей системы неравенств: Целевая функция:

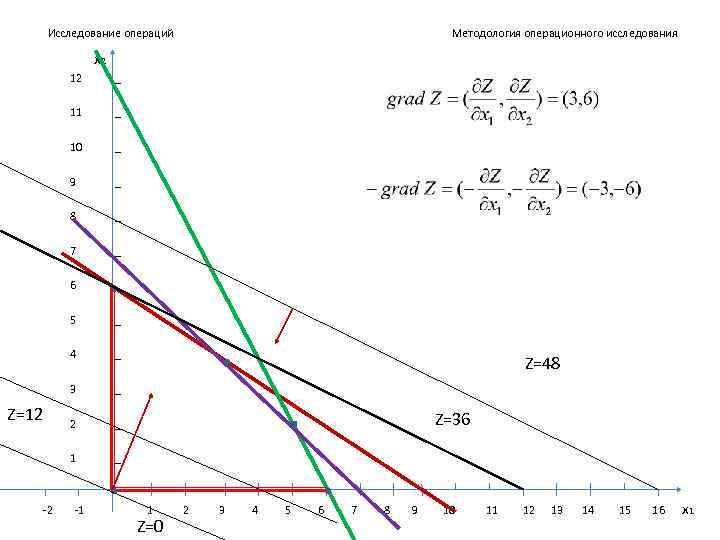Исследование операций Методология операционного исследования x 2 12 11 _ 10 _ 9 _ 8 _ 7 _ 6 _ 5 _ 4 _ 3 Z=12 _ _ 2 1 _ Z=48 Z=36 _ -2 -1 1 2 3 4 5 6 7 8 9 10 Z=0 11 12 13 14 15 16 x 1

Методология операционного исследования Исследование операций 2. Транспортная задача на сети. Пусть задан 6 -ть населенных пунктов, причем некоторые из них связаны между собой дорогами. Имеются 2 -а поставщика, 2 -а потребителя и 2 -а промежуточных транзитных пункта. На каждой из дорог задана стоимость перевозки единицы товара. Для пунктов-поставщиков задан объем товара, который можно из них вывезти. А для пунктов потребителей - объем потребности в данном товаре. Требуется так спланировать перевозки, чтобы удовлетворить запросы пунктов потребителей и чтобы суммарная стоимость перевозок была минимальна. Эта задача транспортного типа. 5 Пр. 1 10 Тр. 1 4 Пр. 2 14 4 Пот. 1 12 3 Пот. 2 12 Тр. 2 Введём переменные - объём товара, перевозимого из пункта производства i через транзитный пункт j в пункт потребления k. Тогда ограничения примут вид: Целевая функция:

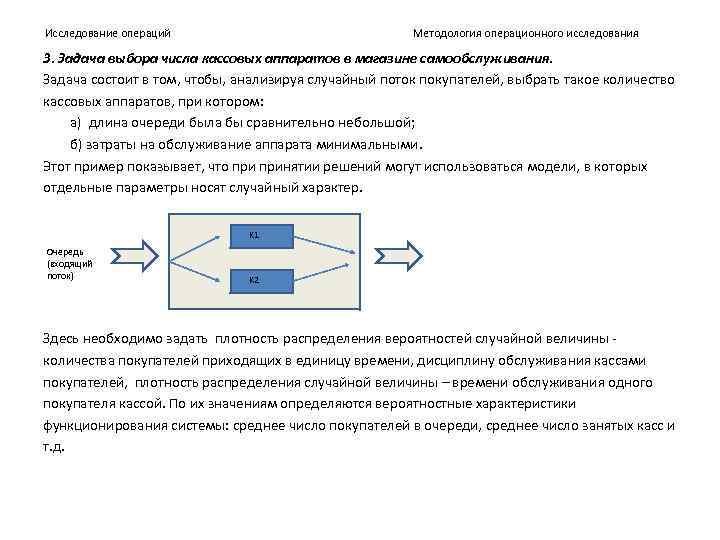Методология операционного исследования Исследование операций 3. Задача выбора числа кассовых аппаратов в магазине самообслуживания. Задача состоит в том, чтобы, анализируя случайный поток покупателей, выбрать такое количество кассовых аппаратов, при котором: а) длина очереди была бы сравнительно небольшой; б) затраты на обслуживание аппарата минимальными. Этот пример показывает, что принятии решений могут использоваться модели, в которых отдельные параметры носят случайный характер. K 1 Очередь (входящий поток) K 2 Здесь необходимо задать плотность распределения вероятностей случайной величины количества покупателей приходящих в единицу времени, дисциплину обслуживания кассами покупателей, плотность распределения случайной величины – времени обслуживания одного покупателя кассой. По их значениям определяются вероятностные характеристики функционирования системы: среднее число покупателей в очереди, среднее число занятых касс и т. д.

Исследование операций Методология операционного исследования 4. Задача оптимального упорядочения. Пусть имеется некоторое устройство (станок), на котором требуется обработать группу деталей. Если на станке обработалась i-ая деталь и после этого на обработку идет j-ая деталь, то известно время настройки или переналадки станка. Известно также время обработки каждой детали на этом станке. Ясно, что суммарное время обработки всех деталей будет зависать от порядка запуска деталей в обработку. Требуется найти такой порядок, при котором суммарное время обработки было бы минимальным. В данной задаче в качестве управляемой переменной нужно выбирать последовательность , определяющую порядок поступления деталей на станок (так называемое расписание). Здесь указывает номер детали поступающей на обработку i-ой. Тогда целевая функция будет иметь вид Если задано n деталей, то существует n! всевозможных порядков запуска деталей в обработку. Уже при n=20 перебор всех вариантов практически невозможен.

Исследование операций Методология операционного исследования 5. Игровая задача. Пусть две стороны A и B имеют противоречивые цели (например, одна сторона – набор вооружений, другая – средства защиты). Для каждой стороны требуется выбрать наилучший для себя способ проведения операций (цель первой – поразить наибольшее число объектов, цели второй – защита наилучшим образом). Оказывается, что такие задачи можно формализовать и для этого необходимо, например, знать число – выигрыш стороны А применении ей i-го варианта действий, если сторона В использует свой j-ый вариант.

Исследование операций Линейное программирование Общая постановка задачи ЛП. Найти план , который (1) при системе ограничений: (2) (3) (4) (5) Z(X) – целевая функция. Множество планов X удовлетворяющих (1)-(5) (обозначим Ω)множество допустимых решений. План X доставляющий экстремальное значение целевой функции называется оптимальным.

Исследование операций Линейное программирование Каноническая форма. Если все ограничения задачи заданы в виде строгих равенств и на все переменные наложено условие неотрицательности, то это задача в канонической форме: при ограничениях

Исследование операций Линейное программирование Переход от задачи на max к задаче на min: Переход к каноническому виду. Вводятся неотрицательные дополнительные переменные

Исследование операций Пример. Перейти к канонической форме: Исходная задача Каноническая форма Линейное программирование

Исследование операций Матричная и векторная форма записи. Обозначим Тогда матричная форма записи: Векторная форма записи: Линейное программирование

Линейное программирование Исследование операций Пример. Исходная задача Матричная форма: Векторная форма: Каноническая форма

Исследование операций Линейное программирование Выпуклость множества допустимых решений. Гиперплоскость в n-мерном пространстве называется множество точек, удовлетворяющих линейному уравнению Полупространство в n-мерном пространстве называется множество точек, удовлетворяющих линейному неравенству Множество точек n-мерного пространства называется выпуклым, если вместе с двумя произвольными оно содержит и соединяющий их отрезок. Если X 1 и X 2 – две конечные точки отрезка, то любую его точку X можно представить как X=λX 1+(1 - λ)X 2, где 0≤ λ ≤ 1. a) Полупространство – выпуклое множество. b) Пересечение любого числа полупространств – выпуклое множество. c) Гиперплоскость выпуклое множество.

Исследование операций Линейное программирование Многогранным множеством называется пересечение конечного числа полупространств. Если многогранное множество ограничено, то оно называется многогранником. Многогранное множество допустимых решений задачи ЛП выпукло. Точку X=λX 1+(1 - λ)X 2 , где 0≤ λ ≤ 1, будем называть выпуклой линейной комбинацией точек X 1 и X 2. Выпуклой линейной комбинацией точек X 1, X 2, …, Xr n-мерного пространства назовём точку a) Выпуклая линейная комбинация произвольного числа допустимых планов задачи ЛП является допустимым планом. Множество называется выпуклым, если вместе с любыми своими точками оно содержит их выпуклую линейную комбинацию. Угловой (крайней) точкой выпуклого множества называют точку , не являющуюся выпуклой линейной комбинацией двух различных точек этого множества. b) Пусть Ω – выпуклый многогранник с крайними точками X 1, X 2, …, Xr. Тогда любая его точка может быть представлена ка выпуклая линейная комбинация крайних точек.