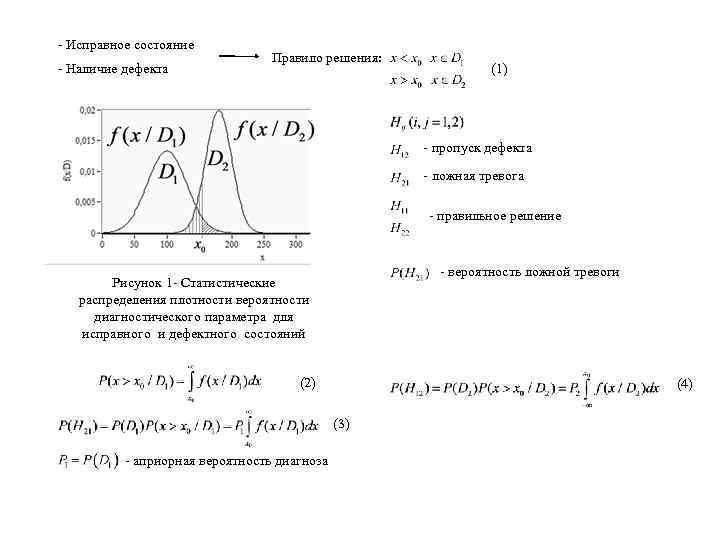
— Исправное состояние — Наличие дефекта Правило решения

- Исправное состояние - Наличие дефекта Правило решения: (1) - пропуск дефекта - ложная тревога - правильное решение - вероятность ложной тревоги Рисунок 1 - Статистические распределения плотности вероятности диагностического параметра для исправного и дефектного состояний (2) (4) (3) - априорная вероятность диагноза

(5) (6) (7) (8) (9) (10) (11) (12) (13) (14)

(15) Пример:

Метод минимального числа ошибочных решений (17) (18) (19) (20) (21) (22) (23)

Метод минимакса (25) (26) (27) (28) (29) (30)

(31) (32) (33) (34) (35)

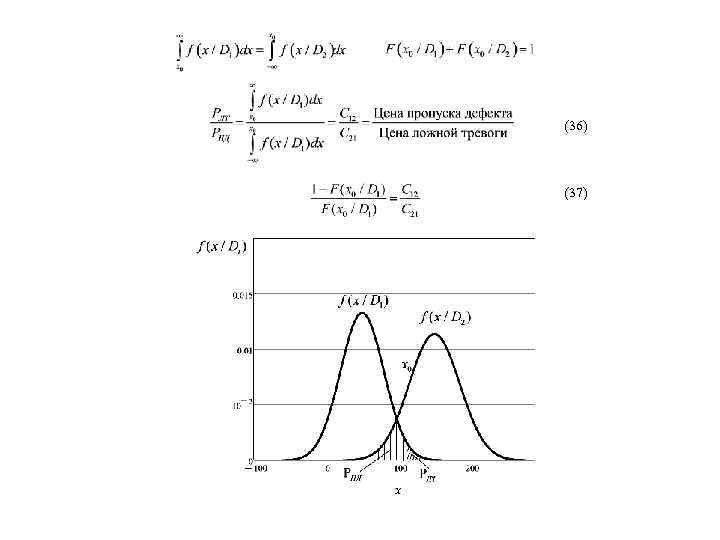(36) (37)

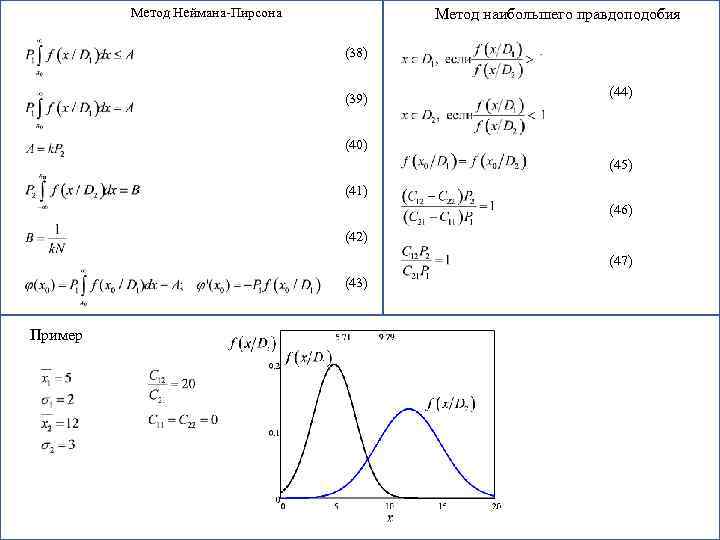Метод Неймана-Пирсона Метод наибольшего правдоподобия (38) (39) (44) (40) (45) (41) (46) (42) (47) (43) Пример

Метод минимального риска Метод минимального числа ошибочных решений Метод минимакса

Метод Неймана-Пирсона Метод наибольшего правдоподобия Таблица – Результаты расчета по методам статистических решений

Статистические решения при наличии зоны неопределенности (1) - отказ от распознавания Определение среднего риска (2) Метод минимального риска при наличии зоны неопределенности (3) (4)

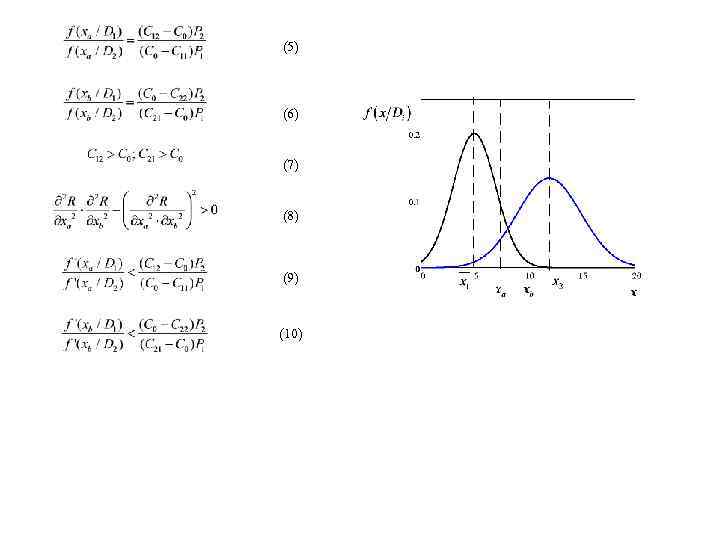(5) (6) (7) (8) (9) (10)

Метод Неймана-Пирсона при наличии зоны неопределенности (12) (13)