Использование теоремы Гаусса для нахождения напряженности и потенциала

Использование теоремы Гаусса для нахождения напряженности и потенциала заряженной плиты Задача 1. Найти напряженность и потенциал электрического поля, созданного заряженной бесконечной плитой толщиной с объемной плотностью заряда. Пусть ось Oz перпендикулярна плите и плоскость является плоскостью симметрии плиты. Тогда в силу симметрии и с учётом того, что плита бесконечна, поле однородно. Имеем: Линии напряжённости перпендикулярны верхней и нижней поверхности плиты и направлены от указанных поверхностей (плита бесконечна). Направления линий напряжённости совпадают направлением нормали верхней и нижней граней параллелепипеда. С нормалями других четырёх граней параллелепипеда угол нормали и линии напряжённости равен градусов.

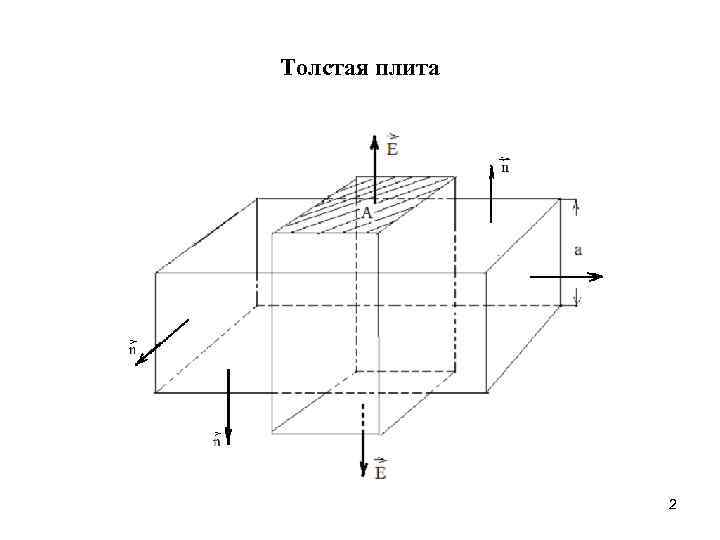Толстая плита 2

Решение задачи Для решения задач будем использовать теорему Гаусса. В качестве гауссовой поверхности будем рассматривать параллелепипед, симметричный относительно плоскости с площадью основания равной и высотой. Следовательно, ненулевой поток образуется только через верхнюю и нижнюю грань параллелепипеда. Запишем теорему Гаусса. Случай а) точка наблюдения внутри плиты Напряженность Потенциал

Случай b). Пусть (точка наблюдения вне плиты) Найдём потенциал в этом случае 4

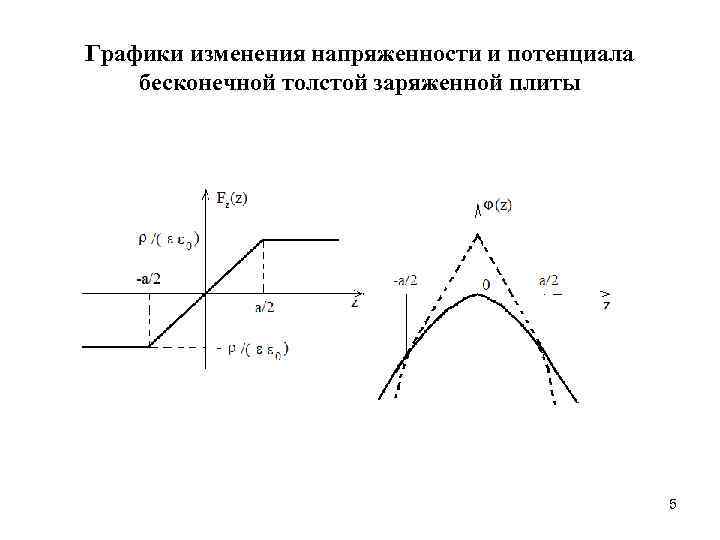Графики изменения напряженности и потенциала бесконечной толстой заряженной плиты 5

Задача 2. Бесконечная плоская плита толщиной заряжена равномерно по объёму с плотностью. Найти потенциал и напряженность электрического поля, созданного плитой, если вещество плиты проводник. Замечание. Заряд распределён не по объёму плиты, а по верхней и нижней поверхностях: Найдем поверхностную плотность заряда В этом случае гауссова поверхность охватывает заряды с двух плоскостей, равные по

Потенциал бесконечной толстой плиты проводника 7

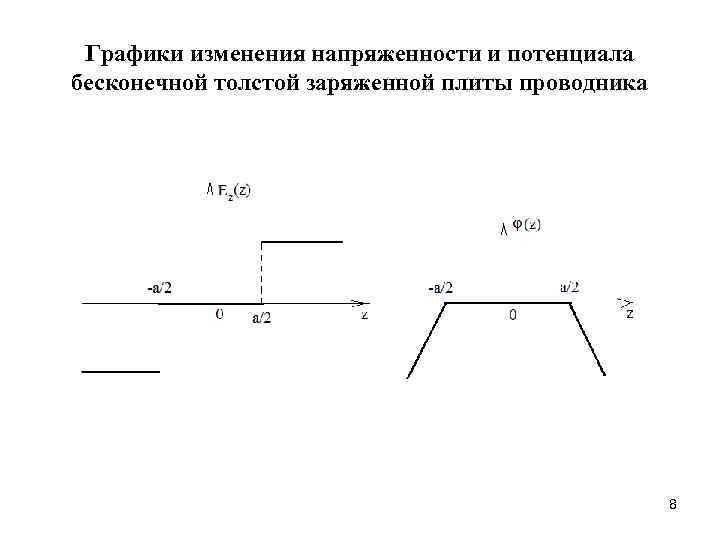Графики изменения напряженности и потенциала бесконечной толстой заряженной плиты проводника 8