Использование средств Excel для финансовых расчетов 1

Использование средств Excel для финансовых расчетов

1. Финансовые функции Excel 2. Подбор параметра 3. Диспетчер сценариев 4. Таблица подстановки

Финансовые функции EXCEL Предназначены для вычисления базовых величин, необходимых для проведения сложных финансовых расчетов

Группы финансовых функций 1. Для анализа инвестиционных проектов 2. Анализа ценных бумаг 3. Для расчета амортизации 4. Вспомогательные функции

Алгоритм расчета результата финансовой функции: 1. В ячейки рабочего листа ввести значения аргументов функции 2. Установить курсор в ячейку для ввода финансовой функции 3. Выполнить: Вставка Функция 4. Выбрать категорию Финансовые

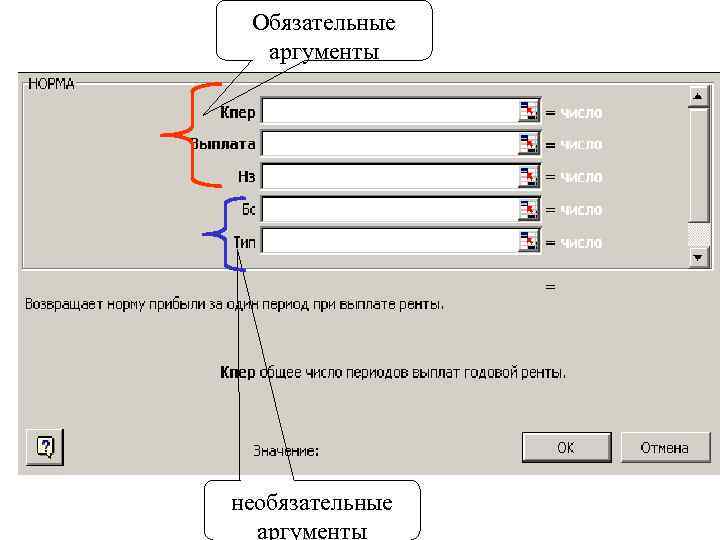Обязательные аргументы необязательные аргументы

В Excel реализовано 15 встроенных и 37 дополнительных финансовых функций Дополнительные функции устанавливаются командой Сервис, Надстройки, Пакет анализа

Функции Excel для расчета финансовых операций по кредитам, займам, ссудам.

Расчеты основаны на концепции временной стоимости денег и предполагают неравноценность денег, относящихся к разным моментам времени

Данные функции позволяют определять: 1. Сумму наращенной стоимости (будущая стоимость) 2. Начальное значение (текущая стоимость) 3. Срок платежа и процентной ставки 4. Расчет периодических платежей, связанных с погашением займов.

Общая формула расчета, которую Excel использует при вычислении финансовых аргументов, связанных с денежными потоками: Формула 1

pmt – фиксированная (неизменная) сумма платежа; n – общее число периодов выплат r – процентная ставка за один период (норма) type – число 0 или 1, обозначающее когда производится выплата: 1 – в начале периода, 0 – в конце периода

pv – текущая стоимость вклада (займа), по которому начисляются проценты по ставке r % n-ое число периодов или текущая стоимость серии фиксированных периодических платежей fv – будущая стоимость вклада (займа) или будущая стоимость серии фиксированных периодических платежей.

Если процентная ставка за период начисления r = 0, то используется формула: Формула 2

Определение будущей стоимости Вложения сделанные сегодня, в будущем составят большую величину (принцип неравноценности денег)

Функция БЗ() рассчитывает будущую стоимость периодических постоянных платежей и будущее значение единой суммы вклада или займа на основе постоянной процентной ставки.

Синтаксис функции: БЗ(норма; число периодов; выплата; нз; тип) Возвращаемое значение функции БЗ() – аргумент fv формулы (1) Формула 3

Задача 1 Рассчитать будущую стоимость единой суммы вклада, по которой начисляются сложное проценты определенное число периодов

Эту величину можно рассчитать по формуле: fv - будущая стоимость вклада (займа) pv -текущая стоимость вклада (займа) n - общее число периодов начисления по % r -процентная ставка по вкладу (займу)

Эта формула соответствует классической формуле расчета наращенной суммы вклада (S) по методу сложных процентов: S = P*(1+i)n P- первоначальный размер долга i – ставка наращения по сложным процентам n – число лет наращения

Сложные проценты применяются в средних и долгосрочных финансово-кредитных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга

n P*(1+i) S= Проценты за n лет равны: i=S–P P*(1+i)n- P = P*((1+i)n-1) q q- множитель наращения по сложным процентам

Присоединение начисленных процентов к основной сумме называют капитализацией процентов

Задача 2 Рассчитать, какая сумма окажется на счете, если 27 тыс. руб. положены на 33 года под 13, 5% годовых. Проценты начисляются каждые полгода.

Решение Проценты начисляются несколько раз в год, значит необходимо рассчитать общее количество периодов начисления процентов и ставку % за период начисления.

% начисляется ежегодно: число периодов = n ставка % за период начисления k % начисляется 1 раз в полгода: число периодов = n*2 % за период начисления k/2

% начисляется каждый квартал n*4 k/4 % начисляется каждый месяц n*12 k/12 % начисляется каждый день n*365 k/365

В задаче общее число периодов = 33*2 Процент начисления = 13, 5%/2 По условию НЗ = -27 Отрицательное число - вложение денег =БЗ(13, 5%/2; 33*2; ; -27) = 2012, 07 тыс. руб

Задача 3 Два варианта инвестирования средств в течение 4 лет при ежегодном взносе 300 тыс. руб. : 1 -й – в начале каждого года под 26% годовых 2 -й – в конце каждого года под 38% годовых Определить сколько денег окажется на счете в конце каждого периода

Решение для 1 -го варианта: норма = 26% число_периодов=4 выплата = - 300 тип = 1 для 2 -го варианта: норма = 38% число_периодов=4 выплата = - 300 тип = 0

Расчеты показали – предпочтительнее первый вариант (инвестировать средства в начале года под 26%)

Функция НПЗ Вычисляет текущую стоимость (NPV) периодических платежей переменной величины как сумму ожидаемых расходов и доходов, дисконтированных нормой процента r

NPV – текущая стоимость периодических и поступлений r – норма дисконтирования (средняя цена капитала 0 n – количество выплат и поступлений valuei – значения выплат и поступлений

Дисконтирование – приведение стоимостной величины, относящейся к будущему, на некоторый, обычно более ранний момент времени (операция обратная наращиванию)

Метод определения чистой текущей стоимости применяется при оценке эффективности инвестиций. Позволяет определить нижнюю границу прибыльности и использовать ее как критерий выбора эффективного проекта

Синтаксис функции НПЗ(норма; значение 1; значение 2; … значение 29) (в XP НПЗ() соответствует ЧПС()

Задача 4 Затраты по проекту на начало его реализации составляют 37 000 р. , ожидаемые доходы в первые 5 лет: 8000 р. , 92000 р. , 10000 р. , 13900 р. , 14500 р. На 6 -й год ожидается убыток – 5000 р. Рассчитать чистую стоимость проекта

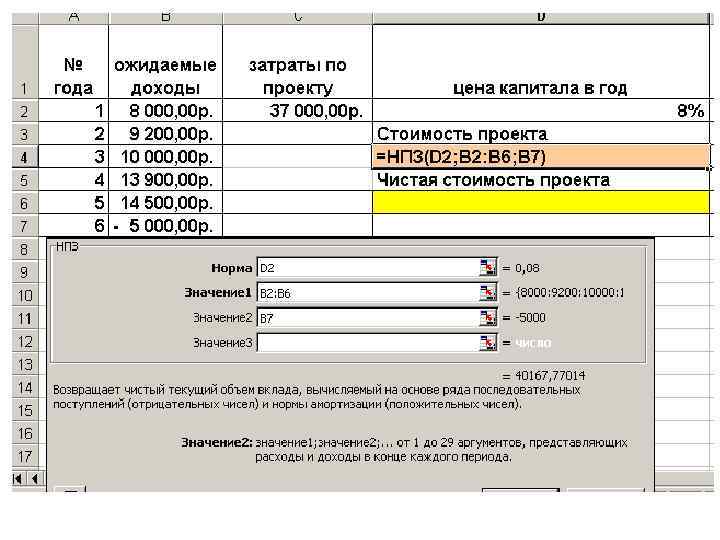
Текущая стоимость проекта : Значение функции НПЗ() -Затраты 3167, 77 р.

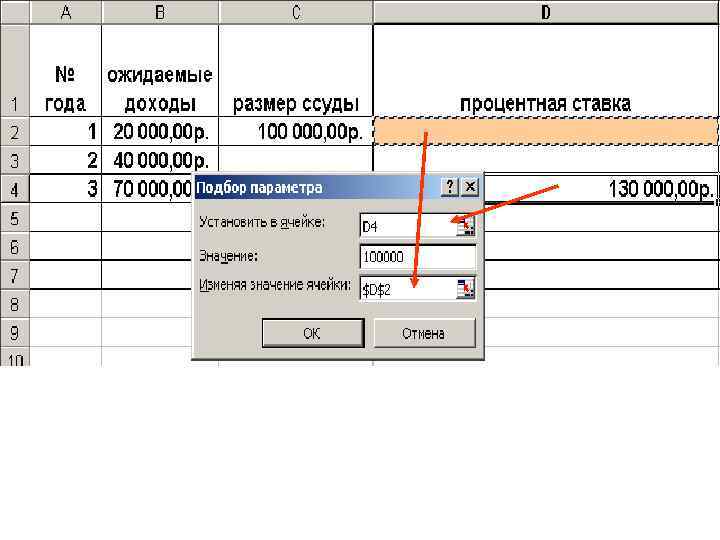
Задача 5 Вас просят дать в долг 100 000 руб. и обещают вернуть через год 20 000 руб. , через 2 года – 40 000 руб. , через 3 года 70 000 руб. При какой % ставке эта сделка выгодна (в банке ставка составляет 10% годовых)?

Решение Задачу следует решить с использованием средства Подбор параметра и функции НПЗ()

=НПЗ(D 2; B 2: B 4)

Задача 6 Оценка эффективности инвестиций В конце года кап. вложения по проекту составят 1280 млн. руб. Ожидается, что в последующие 3 года проект принесет доходы: 420, 490, 550, 590 млн. руб. Рассчитать чистую стоимость проекта для разных норм дисконтирования и объемов кап. вложений

Максимальная величина текущей прибыли достигается при минимальных кап. вложениях и минимальной ставке дисконтирования, например почти одинаковое значение NPV если Кап. вложения = 1310 млн. руб. и норма = 13, 8% Кап. вложения = 1270 млн. руб. и норма = 15%

Функция ПЗ() Возвращает текущий объем вклада на основе постоянных периодических платежей В отличии от НПЗ() допускает внесение денежного взноса в конце или в начале периода, которые должны быть постоянными на весь период инвестиции

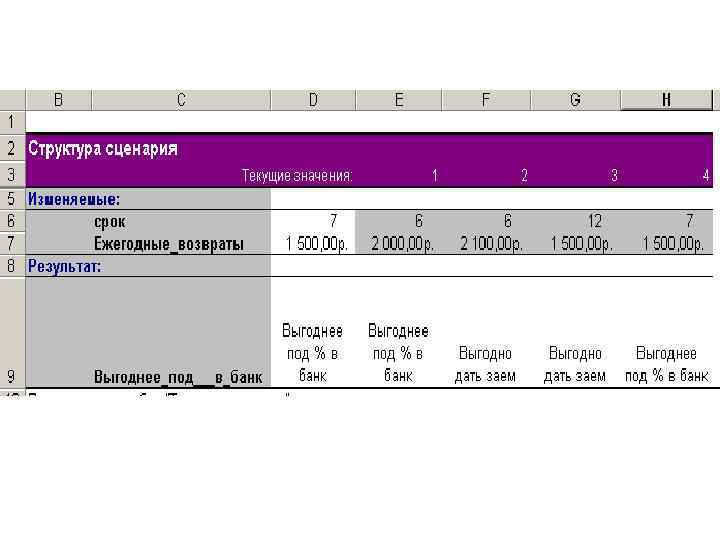
Задача 6 Заем в 10 000 руб. обещают возвращать по 2000 руб. в течение 6 лет. Будет ли выгодна сделка при годовой ставке 7%?

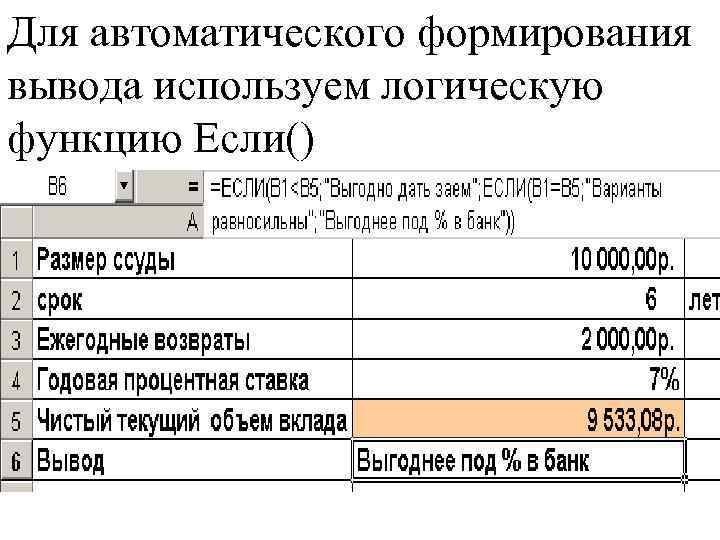Для автоматического формирования вывода используем логическую функцию Если()

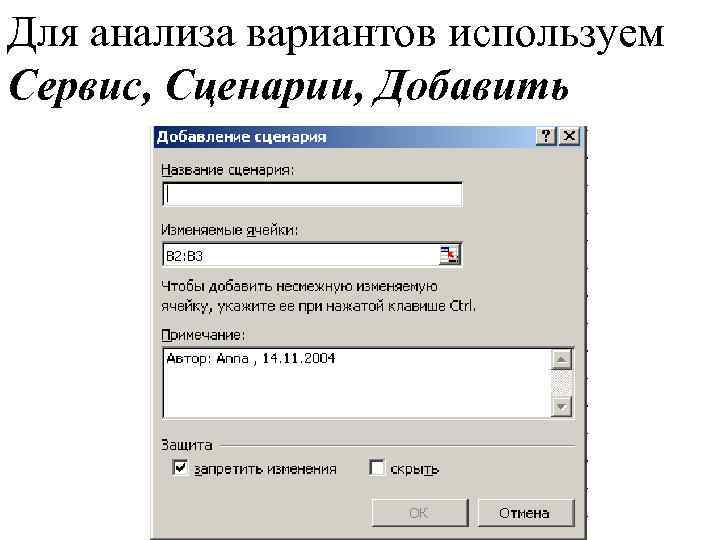Для анализа вариантов используем Сервис, Сценарии, Добавить

Создаем несколько сценариев и выводим отчет