Скачать презентацию Использование симметрии при расчете рам методом перемещений а Скачать презентацию Использование симметрии при расчете рам методом перемещений а

Лекции 27-28.pptx

  • Количество слайдов: 7

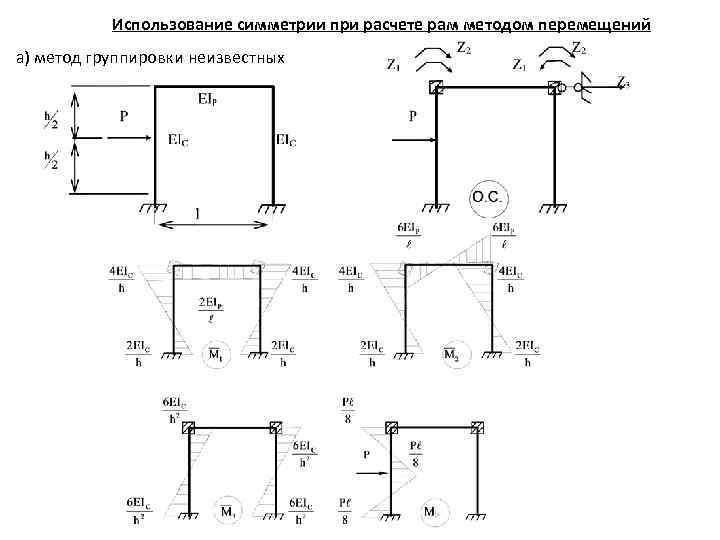
Использование симметрии при расчете рам методом перемещений а) метод группировки неизвестных Использование симметрии при расчете рам методом перемещений а) метод группировки неизвестных

Система из трех уравнений распадается на одно уравнение и систему из двух уравнений с Система из трех уравнений распадается на одно уравнение и систему из двух уравнений с двумя неизвестными.

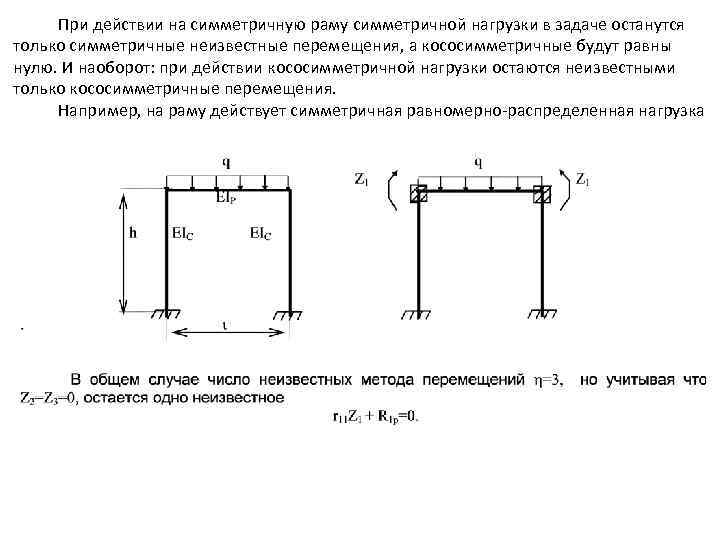При действии на симметричную раму симметричной нагрузки в задаче останутся только симметричные неизвестные При действии на симметричную раму симметричной нагрузки в задаче останутся только симметричные неизвестные перемещения, а кососимметричные будут равны нулю. И наоборот: при действии кососимметричной нагрузки остаются неизвестными только кососимметричные перемещения. Например, на раму действует симметричная равномерно-распределенная нагрузка

Неразрезные балки Неразрезной балкой называется сплошной изгибаемый брус, перекрывающий несколько пролетов и неразрывно связанный Неразрезные балки Неразрезной балкой называется сплошной изгибаемый брус, перекрывающий несколько пролетов и неразрывно связанный с опорами. а) расчет неразрезных балок методом перемещений Заданная схема Основная система Степень линейной подвижности неразрезной балки всегда равна нулю. Степень угловой подвижности равна числу промежуточных опор, т. е. для неразрезных балок число неизвестных метода перемещений определяется = ; т. к. =0. В нашем случае =2.

Уравнение трех моментов, как частный случай метода сил б) рациональная основная система Более рационально Уравнение трех моментов, как частный случай метода сил б) рациональная основная система Более рационально основную систему выбирать, вводя в промежуточные опорные сечения перерезывающие шарниры. В качестве неизвестных, при таком выборе основной системы, выступают опорные моменты. Единичные эпюры распространяются только на два соседних пролета и канонические уравнения метода сил значительно упрощаются, в каждом из них остается не более трех неизвестных.

Уравнение трех моментов, как частный случай метода сил Уравнение трех моментов, как частный случай метода сил

Уравнение трех моментов, как частный случай метода сил Для реализации уравнения 3 -х моментов, Уравнение трех моментов, как частный случай метода сил Для реализации уравнения 3 -х моментов, необходимо: - выбрать основную систему, заменив заданную неразрезную балку системой однопролетных разрезных балок, и в качестве неизвестных принять моменты над промежуточными опорами; - пронумеровать опоры, идя по балке «слева – направо» , и пронумеровать пролеты (номер пролета должен соответствовать номеру правой опоры!!!); - для всех неизвестных опорных моментов записать уравнения трех моментов, - построить грузовую эпюру и вычислить правые части уравнений, - решая систему уравнений, найти неизвестные опорные моменты. Примечание: если одна из крайних опор – жесткое защемление, то со стороны этой опоры вводят фиктивный пролет, длина которого равна нулю.