статистика тема 2.pptx
- Количество слайдов: 56

ИСПОЛЬЗОВАНИЕ МЕТОДОВ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ ДЛЯ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ ЛЕКЦИЯ 2 С. И. Смирнова

Основные понятия Статистические гипотезы систематизируют предположения исследователя. Нулевая гипотеза (H 0) Альтернативная гипотеза (H 1) Это гипотеза об отсутствии различий, это то, что мы хотим опровергнуть, чтобы доказать значимость различий Это гипотеза о значимости различий, это то, что мы хотим доказать (иногда ее называют экспериментальной) Направленные гипотезы H 0: Х 1 не превышает Х 2 H 1: Х 1 превышает Х 2 Ненаправленные гипотезы H 0: Х 1 не отличается от Х 2 H 1: Х 1 отличается от Х 2

Основные понятия Статистический критерий – это решающее правило, которое описывает условия принятия истинной гипотезы и отклонения ложной с высокой степенью вероятности. Чтобы подтвердить или опровергнуть гипотезу, надо сравнить эмпирическое (полученное исследователем) и критическое (табличное) значения критерия.

Основные понятия Уровень статистической значимости – это вероятность того, что мы сочли различия существенными, а они на самом деле случайны. Если говорят, что различия достоверны на 5%-ом уровне значимости, то вероятность того, что они все-таки недостоверны, составляет 0, 05. Исторически сложилось, что в педагогических исследованиях принято считать низшим уровнем статистической значимости 5%-ый уровень (р ≤ 0, 05), достаточным – 1%-ый уровень (р ≤ 0, 01) и высшим – 0, 1%-ый уровень (р ≤ 0, 001).
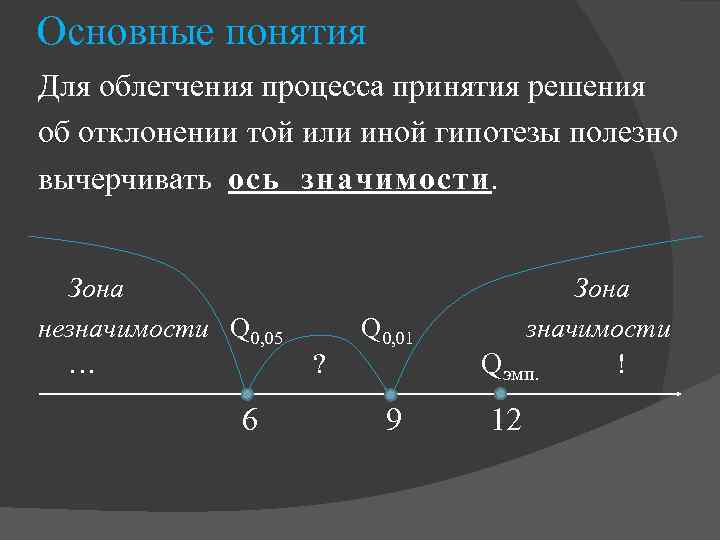
Основные понятия Для облегчения процесса принятия решения об отклонении той или иной гипотезы полезно вычерчивать ось значимости. Зона незначимости Q 0, 05 Q 0, 01 значимости … ? Qэмп. ! 6 9 12

ПРАВИЛА РАНЖИРОВАНИЯ Меньшему значению начисляется меньший ранг. Наименьшему значению начисляется ранг 1. Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений. 2. В случае, если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны. 3. Общая сумма рангов должна совпадать с расчетной, которая вычисляется по формуле: Ri = ½ N (N + 1), где N – общее количество ранжируемых наблюдений. Если суммы не совпадают, необходимо найти ошибку в подсчетах. 1.

ПРАВИЛА РАНЖИРОВАНИЯ Пример. Даны результаты теста 15 учащихся: 8, 3, 8, 5, 5, 3, 6, 7, 2, 10, 9, 6, 9, 10. Упорядочим эти данные в порядке возрастания (строка 1 в таблице). Пронумеруем их по порядку от 1 до 15 (строка 2). Присвоим каждому значению ранг (строка 3) в соответствии с правилами ранжирования и найдем сумму полученных рангов. х 2 3 3 5 5 6 6 7 8 8 9 9 10 10 10 № 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Ri 1 14 14 14 120 2, 5 4, 5 6, 5 8 9, 5 11, 5 Расчетная сумма рангов: Ri = ½ 15 (15 + 1) = ½ 15 16 = 120. (Верно!)

КРИТЕРИИ РАЗЛИЧИЙ Используются для оценки различий между двумя выборками по уровню какого-либо количественно измеренного признака

Q – критерий Розенбаума В каждой выборке должно быть не менее 11 испытуемых. Критерий очень прост в применении. Если Q-критерий выявляет достоверные различия с уровнем значимости p ≤ 0, 01, то это позволяет избежать трудностей применения других критериев. Если же Q-критерий не выявляет достоверные различия, то это еще не означает, что их действительно нет. В этом случае необходимо применить более мощный критерий (например, критерий * – угловое преобразование Фишера).
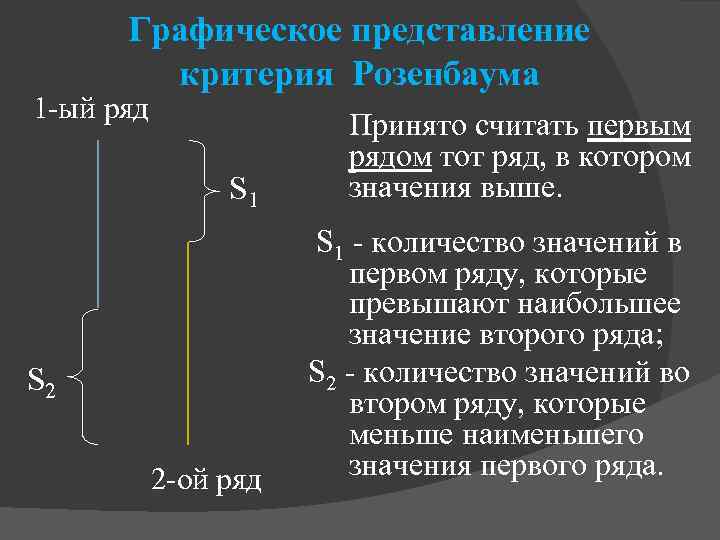
Графическое представление критерия Розенбаума 1 -ый ряд S 1 Принято считать первым рядом тот ряд, в котором значения выше. 2 -ой ряд S 1 - количество значений в первом ряду, которые превышают наибольшее значение второго ряда; S 2 - количество значений во втором ряду, которые меньше наименьшего значения первого ряда. S 2
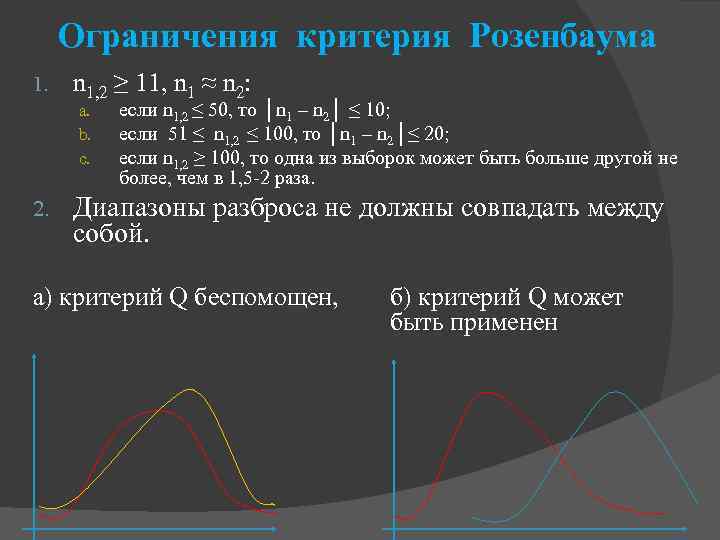
Ограничения критерия Розенбаума 1. n 1, 2 ≥ 11, n 1 ≈ n 2: a. b. c. 2. если n 1, 2 ≤ 50, то │n 1 – n 2│ ≤ 10; если 51 ≤ n 1, 2 ≤ 100, то │n 1 – n 2│≤ 20; если n 1, 2 ≥ 100, то одна из выборок может быть больше другой не более, чем в 1, 5 -2 раза. Диапазоны разброса не должны совпадать между собой. а) критерий Q беспомощен, б) критерий Q может быть применен

Подсчет критерия Q Розенбаума. Алгоритм. Проверить выполнимость ограничений. Упорядочить значения отдельно для каждой выборки по степени возрастания признака. Считать выборкой 1 ту, в которой значения предположительно выше. 3. Сформулировать гипотезы. 4. Определить максимальное значение в выборке 2. 5. Подсчитать количество значений в выборке 1, которые выше максимального значения в выборке 2. Обозначить полученную величину s 1. 6. Определить самое низкое значение в выборке 1. 7. Подсчитать количество значений в выборке 2, которые ниже минимального значения в выборке 1. Обозначить полученную величину s 2. 8. Подсчитать эмпирическое значение Q по формуле Qэмп. = s 1 + s 2. 9. По таблице определить критическое значение Q для данных n 1 и n 2. 10. Вычертить ось значимости и принять решение. 1. 2.
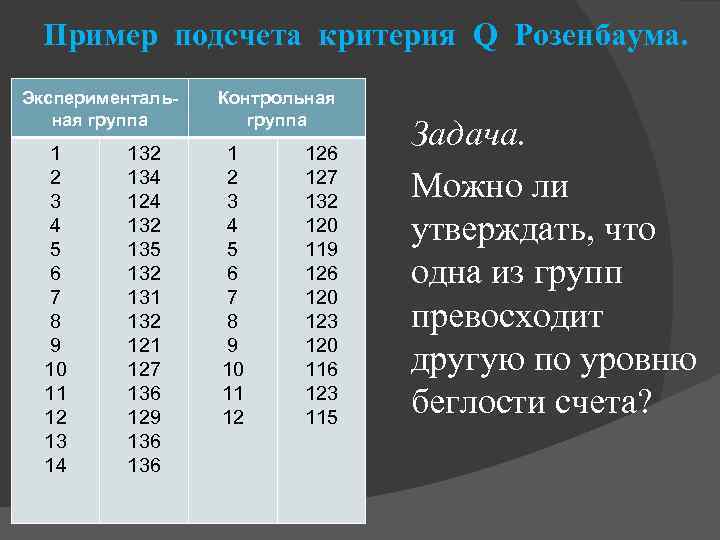
Пример подсчета критерия Q Розенбаума. Экспериментальная группа 1 2 3 4 5 6 7 8 9 10 11 12 13 14 132 134 124 132 135 132 131 132 121 127 136 129 136 Контрольная группа 1 2 3 4 5 6 7 8 9 10 11 12 126 127 132 120 119 126 120 123 120 116 123 115 Задача. Можно ли утверждать, что одна из групп превосходит другую по уровню беглости счета?

Пример подсчета критерия Q Розенбаума. Проверим выполнимость ограничений: n 1, 2 ≥ 11 и n 1 ≈ n 2. 2. Будем считать выборкой 1 экспериментальную группу, так как в ней значения выше. 3. Сформулируем гипотезы. H 0: уровень беглости счета в экспериментальной группе не превосходит уровень беглости счета в контрольной группе. H 1: уровень беглости счета в экспериментальной группе превосходит уровень беглости счета в контрольной группе. 1.

Пример подсчета критерия Q Розенбаума 4. 5. 6. 7. 8. 9. Определим максимальное значение в выборке 2 – 132. Подсчитаем количество значений в выборке 1, которые выше 132: s 1 = 5. Определим самое низкое значение в выборке 1 – 121. Подсчитаем количество значений в выборке 2, которые ниже 121: s 2 = 6. Подсчитать эмпирическое значение Qэмп. = 5 + 6 = 11. По таблице определим критические значения Q: 7 (p ≤ 0, 05) Qкр. = 9 (p ≤ 0, 01)
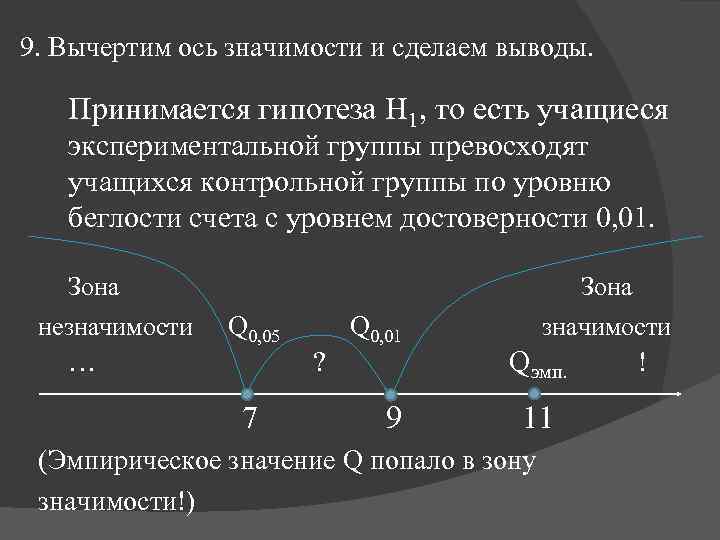
9. Вычертим ось значимости и сделаем выводы. Принимается гипотеза H 1, то есть учащиеся экспериментальной группы превосходят учащихся контрольной группы по уровню беглости счета с уровнем достоверности 0, 01. Зона незначимости Q 0, 05 Q 0, 01 значимости … ? Qэмп. ! Зона 7 9 11 (Эмпирическое значение Q попало в зону значимости!)

U – критерий Манна-Уитни позволяет выявлять различия между малыми выборками (когда n 1, n 2 ≥ 3 или n 1 = 2, n 2 ≥ 5), является более мощным, чем критерий Розенбаума, определяет, достаточно ли мала зона перекрещивающихся значений между двумя рядами (чем меньше эта зона, тем более вероятно, что различия достоверны).

Графическое представление U-критерия Манна-Уитни 1 ряд 2 ряд а) Область наложения значений слишком мала. Различия, возможно, достоверны. Определить это точно можно с помощью Uкритерия 2 ряд в) Область наложения значений достаточно обширна. Различия, возможно, несущественны. Определить это можно с помощью точного подсчета U-критерия с) Область наложения значений настолько обширна, что различия скрадываются.

1. 2. 3. 4. Алгоритм подсчета критерия U – Манна-Уитни Расположить все значения в единый ряд по степени нарастания признака, не зависимо от того, к какой выборке они относятся. Проранжировать значения (всего рангов получится n 1 + n 2). Подсчитать сумму рангов отдельно для каждой выборки. Проверить, совпадает ли общая сумма рангов с расчетной. Определить большую из двух ранговых сумм.

Алгоритм подсчета критерия U – Манна-Уитни 5. Определить эмпирическое значение U: n 1, 2 – количество испытуемых в выборках 1 и 2, Tх – большая из двух ранговых сумм, nх – количество испытуемых в выборке с большей суммой рангов. Определить критические значения U по таблицам. 7. Вычертить ось значимости и принять решение. 6.

КРИТЕРИИ ИЗМЕНЕНИЙ Для сопоставления замеров «до» и «после» экспериментального воздействия отдельно по экспериментальной и контрольной группам

Оценка достоверности сдвига в значениях исследуемого признака Временной сдвиг – сопоставление показателей у одних и тех же испытуемых по одним и тем же методикам, но в разное время. Ситуационный сдвиг – сопоставление показателей, полученных в разных условиях измерения (например, в условиях «покоя» и «стресса» ). Сдвиг под влиянием – сопоставление показателей, полученных до и после экспериментального воздействия (если сдвиги окажутся статистически достоверными, то это позволит утверждать, что воздействия были эффективными).

Оценка достоверности сдвига в значениях исследуемого признака Сдвиги, которые кажутся преобладающими, называют типичными. Сдвиги более редкого направления называют нетипичными. Если показатели не изменяются, то сдвиги считают нулевыми (нулевые сдвиги исключают из рассмотрения, число наблюдений уменьшается на число нулевых сдвигов).

G – критерий знаков применяется для установления общего направления сдвига исследуемого признака (изменяются в сторону улучшения, повышения или, наоборот, в сторону ухудшения, понижения), применяется к тем сдвигам, которые определены качественно или измерены количественно, определяет, не слишком ли много наблюдается «нетипичных сдвигов» , чтобы сдвиг в типичном направлении считать статистически значимым. Количество наблюдений в группе: от 5 до 300. Gэмп. – это количество нетипичных сдвигов (чем меньше Gэмп. , тем более вероятно, что сдвиг в типичном направлении статистически достоверен).

Алгоритм подсчета критерия знаков G 1. 2. 3. 4. 5. 6. Подсчитать количество нулевых реакций и исключить их из рассмотрения. Определить преобладающее (типичное) направление изменений. Сформулировать гипотезы. Определить число нетипичных сдвигов. Считать это число эмпирическим значением G. Определить по таблицам критические значения G для данного n. Вычертить ось значимости и принять решение.

Пример подсчета критерия знаков G Задача. На одной и той же группе учащихся произведены два замера некоторого признака «до обучения» и «после обучения» . Можно ли считать обучение эффективным, если результаты таковы: Испытуемые 1 2 Значения 8 6 «до обучения» Значения «после 12 8 обучения» 3 4 5 6 7 8 9 10 3 2 5 5 7 8 10 12 3 5 10 4 9 8 9 15
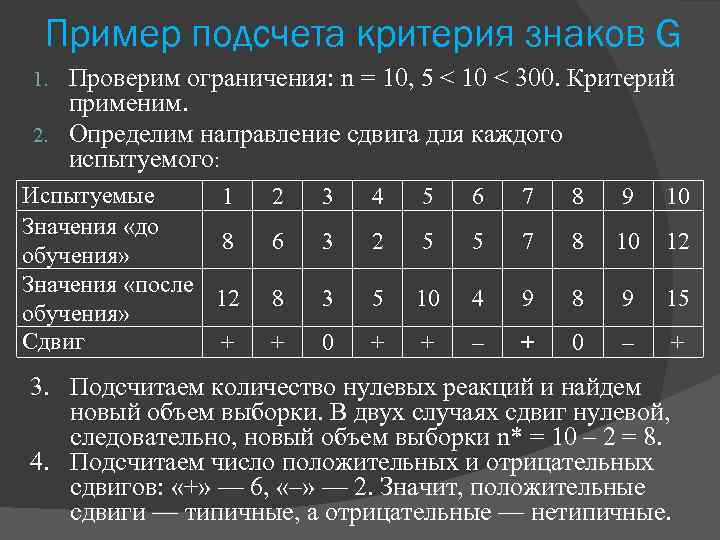
Пример подсчета критерия знаков G Проверим ограничения: n = 10, 5 < 10 < 300. Критерий применим. 2. Определим направление сдвига для каждого испытуемого: 1. Испытуемые Значения «до обучения» Значения «после обучения» Сдвиг 1 2 3 4 5 6 7 8 9 10 8 6 3 2 5 5 7 8 10 12 12 8 3 5 10 4 9 8 9 15 + + 0 + + – + 0 – + 3. Подсчитаем количество нулевых реакций и найдем новый объем выборки. В двух случаях сдвиг нулевой, следовательно, новый объем выборки n* = 10 – 2 = 8. 4. Подсчитаем число положительных и отрицательных сдвигов: «+» — 6, «–» — 2. Значит, положительные сдвиги — типичные, а отрицательные — нетипичные.

Пример подсчета критерия знаков G Сформулируем гипотезы: H 0: Улучшение показателей (сдвиг показателей в типичную сторону) является случайным. H 1: Улучшение показателей (сдвиг показателей в типичную сторону) является неслучайным. 6. Найдем Gэмп. , оно равно числу нетипичных сдвигов. Gэмп. = 2. 7. Найдем критические значения G для n* = 8. Gкр. (р ≤ 0, 05) = 1 и Gкр. (р ≤ 0, 01) = 0. 8. Изобразим ось значимости: 5. ! ? … Зона значимости Зона незначимости 0 1 Gэмп 9. Так как Gэмп. > Gкр. (р ≤ 0, 05), то H 0 принимается, то есть различия случайны.

Т – критерий Вилкоксона применяется для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых; позволяет установить не только направленность изменений, но и их выраженность (является ли сдвиг показателей в каком-то одном направлении более интенсивным, чем в другом); эффективен в том случае, если сдвиги между вторым и первым замерами варьируют в достаточно большом диапазоне (если сдвиги изменяются, например, от -35 до +45, то имеет смысл их ранжировать и потом суммировать ранги); количество испытуемых, прошедших измерения в двух условиях, – от 5 до 50 человек.
Графическое представление критерия Т а) б) в)

Алгоритм подсчета критерия Т 1. 2. 3. 4. 5. Вычислить разность между индивидуальными значениями испытуемых во втором и первом замерах ( «после» – «до» ). Определить типичный сдвиг и сформулировать гипотезы. Найти абсолютные значения разности (модуль) и проранжировать их. Проверить совпадение полученной суммы рангов с расчетной. Отметить сдвиги в «нетипичном» направлении и подсчитать сумму соответствующих им рангов. Присвоить это значение Тэмп. . Определить критические значения Т по таблицам. Начертить ось значимости и сделать выводы.

Пример подсчета критерия Т У 11 испытуемых в двух разных условиях были измерены показатели чтения (число слов в минуту): а) в спокойном состоянии, б) при контрольной проверке с внешним проверяющим. Подтвердилась ли гипотеза проверяющего о том, что контрольная ситуация способствует более успешному выполнению задания? 1 2 3 4 5 6 7 8 10 11 а 64 77 74 95 105 83 73 75 101 97 78 б 64 60 78 96 78 76 91 76 9 99 121 84
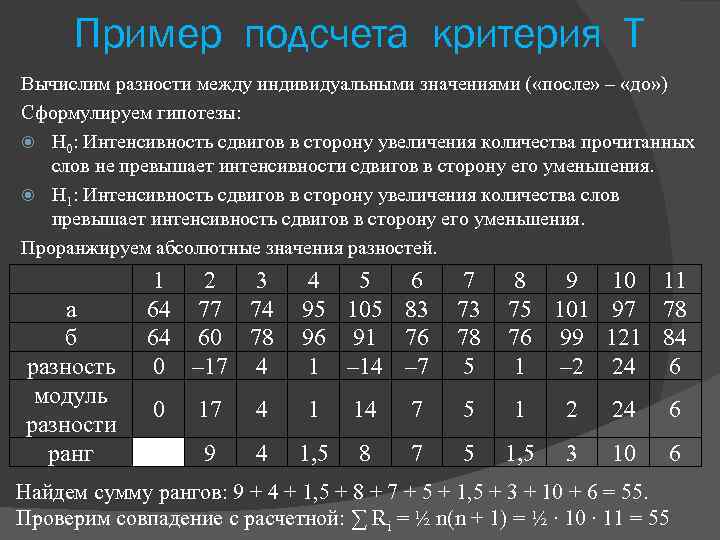
Пример подсчета критерия Т Вычислим разности между индивидуальными значениями ( «после» – «до» ) Сформулируем гипотезы: H 0: Интенсивность сдвигов в сторону увеличения количества прочитанных слов не превышает интенсивности сдвигов в сторону его уменьшения. H 1: Интенсивность сдвигов в сторону увеличения количества слов превышает интенсивность сдвигов в сторону его уменьшения. Проранжируем абсолютные значения разностей. а б разность модуль разности ранг 1 2 3 64 77 74 64 60 78 0 – 17 4 4 5 6 95 105 83 96 91 76 1 – 14 – 7 7 73 78 5 8 9 10 11 75 101 97 78 76 99 121 84 1 – 2 24 6 0 17 4 1 14 7 5 1 2 24 6 9 4 1, 5 8 7 5 1, 5 3 10 6 Найдем сумму рангов: 9 + 4 + 1, 5 + 8 + 7 + 5 + 1, 5 + 3 + 10 + 6 = 55. Проверим совпадение с расчетной: ∑ Ri = ½ n(n + 1) = ½ ∙ 10 ∙ 11 = 55

Пример подсчета критерия Т Отметим ранги, соответствующие сдвигам в нетипичном (отрицательном) направлении. Найдем их сумму: Тэмп. = 9 + 8 + 7 + 3 = 27. а б разность модуль разности ранг 1 2 3 64 77 74 64 60 78 0 – 17 4 4 5 6 95 105 83 96 91 76 1 – 14 – 7 7 73 78 5 8 9 10 11 75 101 97 78 76 99 121 84 1 – 2 24 6 0 1 5 1 17 4 9 √ 4 14 7 1, 5 8 √ 7 √ 5 2 1, 5 3 √ Для n = 10 найдем критические значения по таблицам: 24 6 10 6
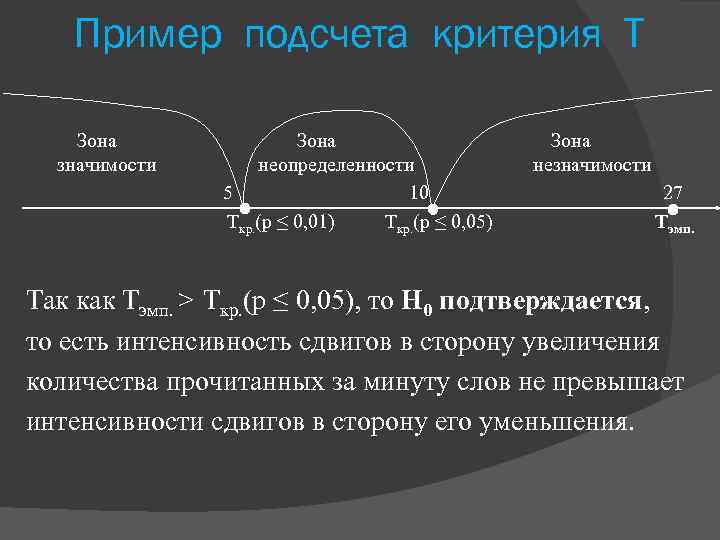
Пример подсчета критерия Т Зона Зона значимости неопределенности незначимости 5 10 27 Ткр. (р ≤ 0, 01) Ткр. (р ≤ 0, 05) Тэмп. Так как Тэмп. > Ткр. (р ≤ 0, 05), то H 0 подтверждается, то есть интенсивность сдвигов в сторону увеличения количества прочитанных за минуту слов не превышает интенсивности сдвигов в сторону его уменьшения.

Критерий χr 2 Фридмана применяется для сопоставления показателей, измеренных в трех и более условиях на одной и той же выборке испытуемых; эмпирическое значение критерия указывает на то, насколько различаются суммы рангов по разным условиям; ограничения: не менее двух испытуемых, каждый из которых прошел не менее трех замеров. При с = 3 число испытуемых n ≤ 9.

Алгоритм подсчета критерия χr 2 Фридмана Проранжировать индивидуальные значения первого испытуемого, полученные им в первом, втором и т. д. замерах. 2. Проделать тоже самое относительно других испытуемых. 3. Просуммировать ранги по условиям, в которых осуществлялись замеры. Проверить совпадение общей суммы рангов с расчетной по формуле: 1.

Алгоритм подсчета критерия χr 2 Фридмана 4. Определить эмпирическое значение по формуле: где с – количество условий, n – количество испытуемых, Тj – суммы рангов по каждому из условий. 5. Определить уровни статистической значимости для χr 2 эмп. 6. При большем количестве условий или испытуемых определить количество степеней свободы и определить критические значения при данном числе степеней свободы.

Многофункциональные критерии Позволяют определить, какая доля испытуемых характеризуется желаемым эффектом, а какая доля этим эффектом не характеризуется

Критерий φ* Фишера Позволяет определить, какая доля испытуемых характеризуется желаемым эффектом, а какая этим эффектом не характеризуется. 2. Используется для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта 3. Число испытуемых может быть небольшим. 4. Признак может быть измерен качественно или количественно. 1.

Алгоритм подсчета критерия φ* Фишера Проверить выполнимость ограничений. 2. Сформулировать гипотезы H 0 и H 1. 3. Разделить испытуемых на тех, у кого «есть эффект» и тех, у кого «нет эффекта» . 4. Начертить четырехклеточную таблицу из двух столбцов и двух строк. Первый столбец – «есть эффект» ; второй столбец – «нет эффекта» , первая строка сверху – первая группа (выборка); вторая строка – вторая группа. Заполнить таблицу. 1.

Алгоритм подсчета критерия φ* Фишера 5. Подсчитать сумму по двум верхним ячейкам. Она должна совпадать с количеством испытуемых в первой группе. 6. Подсчитать сумму по двум нижним ячейкам. Она должна совпадать с количеством испытуемых во второй группе. 7. Определить процентные доли испытуемых, у которых «есть эффект» , путем отнесения их количества к общему количеству испытуемых в данной группе (выборке). Записать полученные процентные доли соответственно в левой верхней и левой нижней ячейках таблицы в скобках, чтобы не перепутать их с абсолютными значениями.

Алгоритм подсчета критерия φ* Фишера 8. Проверить, не равняется ли одна из сопоставляемых процентных долей нулю. Если это так, попробовать изменить это, сдвинув точку разделения групп в ту или иную сторону. Если это невозможно, отказаться от критерия φ* и использовать критерий χ2. 9. Определить по таблицам величины углов φ* для каждой из сопоставляемых процентных долей.

Алгоритм подсчета критерия φ* Фишера 10. Подсчитать φ*эмп. по формуле: * = ( 1 - 2) n 1 n 2 / (n 1 + n 2), где 1 – угол, соответствующий большей процентной доле, 2 – угол, соответствующий меньшей процентной доле 11. Сопоставить полученное значение φ* с критическими значениями. 12. Если φ*эмп. ≥ φ*кр. , то Н 0 отвергается. 13. При необходимости определить точный уровень значимости полученного φ*эмп. по таблицам.

Пример подсчета критерия φ* Сравниваются две группы студентов по успешности решения новой задачи. В первой группе из 20 человек справились с решением задачи 12 человек. Во второй выборке из 25 человек справились с решением задачи 10 человек. Достоверны ли различия по указанному признаку? Будем считать эффектом успех в решении задачи, а отсутствием эффекта — неудачу в ее решении. Сформулируем гипотезы: Н 0: Доля студентов, справившихся с задачей, в первой группе не больше, чем во второй. Н 1: Доля студентов, справившихся с задачей, в первой группе больше, чем во второй.
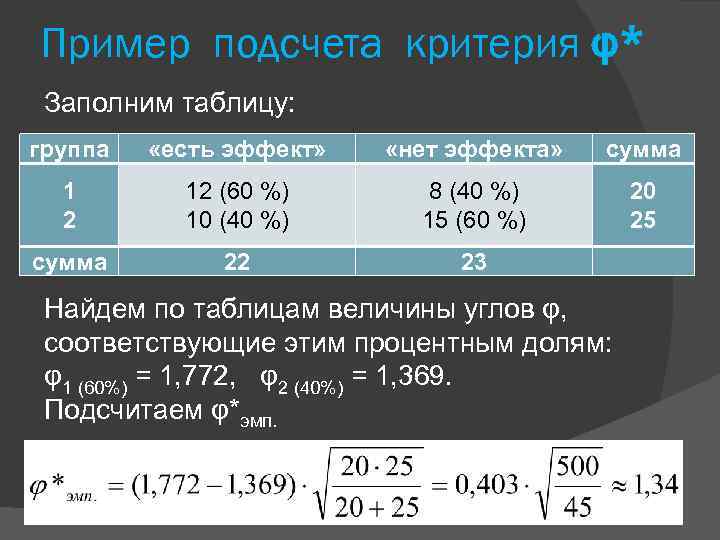
Пример подсчета критерия φ* Заполним таблицу: группа «есть эффект» «нет эффекта» сумма 1 2 12 (60 %) 10 (40 %) 8 (40 %) 15 (60 %) 20 25 сумма 22 23 Найдем по таблицам величины углов φ, соответствующие этим процентным долям: φ1 (60%) = 1, 772, φ2 (40%) = 1, 369. Подсчитаем φ*эмп.

Пример подсчета критерия φ* Начертим ось значимости: φ *0, 05 φ*0, 01 . . . φ*эмп. ? ! 1, 34 1, 64 2, 31 φ*эмп. < φ*кр. , т. е. φ*эмп. находится в зоне незначимости. Следовательно, принимается нулевая гипотеза. Ответ: различия по успешности решения новой задачи в данных группах студентов недостоверны.

Задача Пять испытуемых решали анаграммы (КРУА; АЛСТЬ; ИНААМШ). Достоверны ли различия во времени решения испытуемыми анаграмм? 1 2 3 4 5 Анаграмма 1 t (сек. ) 5 7 2 2 35 Анаграмма 2 t (сек. ) 235 604 93 171 141 Анаграмма 3 t (сек. ) 7 20 5 8 7

Пример решения задачи В группе испытуемых численностью 5 человек проведены 3 замера. Требуется установить наличие изменений от одного замера к другому. Признак измерен количественно. Для решения такой задачи можно воспользоваться критерием изменений χr 2 Фридмана

Пример решения задачи Сформулируем гипотезы: H 0: Между временем решения испытуемыми данных диаграмм существуют лишь случайные различия. H 1: Между временем решения испытуемыми данных диаграмм существуют неслучайные различия.
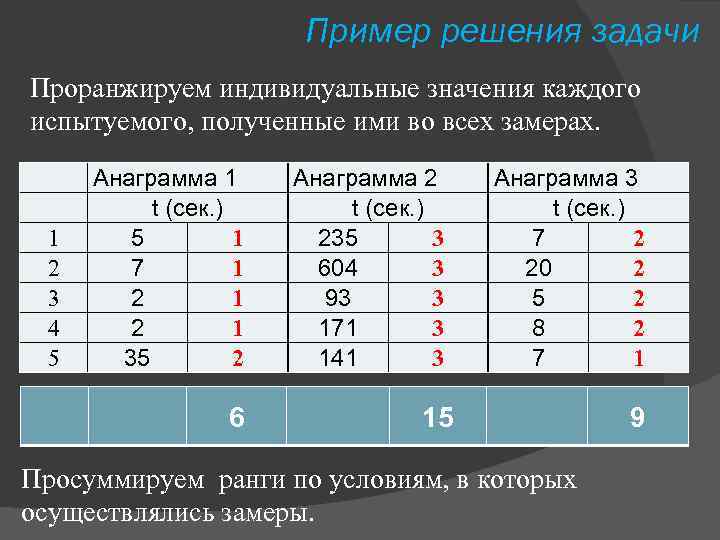
Пример решения задачи Проранжируем индивидуальные значения каждого испытуемого, полученные ими во всех замерах. 1 2 3 4 5 Анаграмма 1 t (сек. ) 1 5 1 7 1 2 2 35 6 Анаграмма 2 t (сек. ) 3 235 3 604 3 93 3 171 3 141 Анаграмма 3 t (сек. ) 2 7 2 20 2 5 2 8 1 7 15 Просуммируем ранги по условиям, в которых осуществлялись замеры. 9

Пример решения задачи Проверим совпадение полученной суммы рангов ∑ Ri = 6 + 15 + 9 = 30 с расчетной:

Пример решения задачи Определим эмпирическое значение по формуле: χr 2 эмп = [12 / (5 ∙ 3 ∙ 4)] ∙ [36 + 225 + 81] – 3 ∙ 5 ∙ 4 = 0, 2 ∙ 342 – 60 = 68, 4 – 60 = 8, 4 Определим уровень статистической значимости для χr 2 эмп. = 8, 4. p = 0, 0085. Уровень значимости достаточный, значит, различия неслучайные.
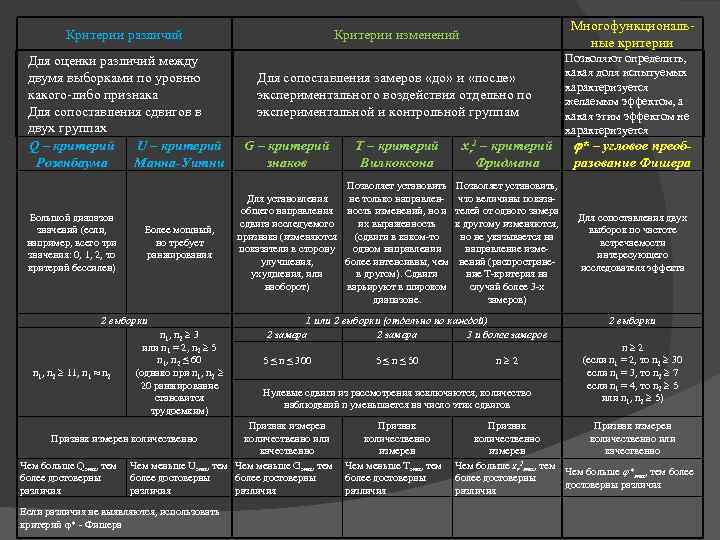
Критерии различий Для оценки различий между двумя выборками по уровню какого-либо признака Для сопоставления сдвигов в двух группах Q – критерий U – критерий Розенбаума Манна-Уитни Большой диапазон значений (если, например, всего три значения: 0, 1, 2, то критерий бессилен) Более мощный, но требует ранжирования 2 выборки n 1, n 2 11, n 1 n 2 n 1, n 2 3 или n 1 = 2, n 2 5 n 1, n 2 ≤ 60 (однако при n 1, n 2 20 ранжирование становится трудоемким) Чем больше Qэмп, тем более достоверны различия Для сопоставления замеров «до» и «после» экспериментального воздействия отдельно по экспериментальной и контрольной группам G – критерий знаков Т – критерий Вилкоксона xr 2 – критерий Фридмана Для установления общего направления сдвига исследуемого признака (изменяются показатели в сторону улучшения, ухудшения, или наоборот) Позволяет установить не только направленность изменений, но и их выраженность (сдвиги в каком-то одном направлении более интенсивны, чем в другом). Сдвиги варьируют в широком диапазоне. Позволяет установить, что величины показателей от одного замера к другому изменяются, но не указывается на направление изменений (распространение Т-критерия на случай более 3 -х замеров) 1 или 2 выборки (отдельно по каждой) 2 замера 3 и более замеров 5 ≤ n ≤ 300 5 ≤ n ≤ 50 Если различия не выявляются, использовать критерий * - Фишера n 2 Нулевые сдвиги из рассмотрения исключаются, количество наблюдений n уменьшается на число этих сдвигов Признак измерен Признак количественно или количественно качественно измерен Чем меньше Uэмп, тем Чем меньше Gэмп, тем Чем меньше Тэмп, тем более достоверны различия Признак измерен количественно Многофункциональные критерии Критерии изменений Позволяют определить, какая доля испытуемых характеризуется желаемым эффектом, а какая этим эффектом не характеризуется * – угловое преобразование Фишера Для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта 2 выборки n 2 (если n 1 = 2, то n 2 30 если n 1 = 3, то n 2 7 если n 1 = 4, то n 2 5 или n 1, n 2 5) Признак измерен количественно или измерен качественно 2 Чем больше xr эмп, тем Чем больше *эмп, тем более достоверны различия

ГИПОТЕЗЫ И ОСНОВНЫЕ ФОРМУЛЫ, ИСПОЛЬЗУЕМЫЕ ПРИ ПОДСЧЕТЕ КРИТЕРИЕВ Критерий Розенбаума Q Р Р Критерий Вилкоксона Т Критерий Фридмана x r 2 Угловое преобразование Фишера * Альтернативная гипотеза Формула Уровень признака в выборке 1 не Уровень признака в выборке Qэмп. = S 1 + S 2 S 1 превышает уровень признака в 1 превышает уровень S 2 выборке 2. признака в выборке 2. Манна-Уитни Уровень признака в группе 2 не U ниже уровня признака в группе 1. Критерий знаков G Р Нулевая гипотеза Преобладание типичного направления сдвига является случайным Интенсивность сдвигов в типичном направлении не превосходит интенсивности сдвигов в нетипичном направлении Между показателями, полученными в разных условиях, существуют лишь случайные различия Uэмп. = n 1 n 2 + ½ nх (nх + 1) – Tх Уровень признака в группе 2 Tх – большая из двух ранговых сумм ниже уровня признака в nх – кол-во испытуемых в группе с группе 1. большей суммой рангов Gэмп. – количество нетипичных Преобладание типичного сдвигов направления сдвига не является случайным Интенсивность сдвигов в типичном направлении превышает интенсивность сдвигов в нетипичном направлении Между показателями, полученными в разных условиях, существуют неслучайные различия Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 больше, 1 не больше, чем в выборке 2. Тэмп. = Rr Rr – ранговые значения сдвигов с более редким знаком xr 2 эмп = [12/n c (c+1)] (Tj 2) – 3 n(c+1) c – количество условий n – количество испытуемых Тj – суммы рангов по каждому из условий * = ( 1 - 2) n 1 n 2(n 1 + n 2) 1 –угол, соответствующий большей процентной доле 2–угол, соответствующий меньшей процентной доле

Спасибо за внимание!
статистика тема 2.pptx