Искусственные нейронные сети История Биологический нейрон

Искусственные нейронные сети

История

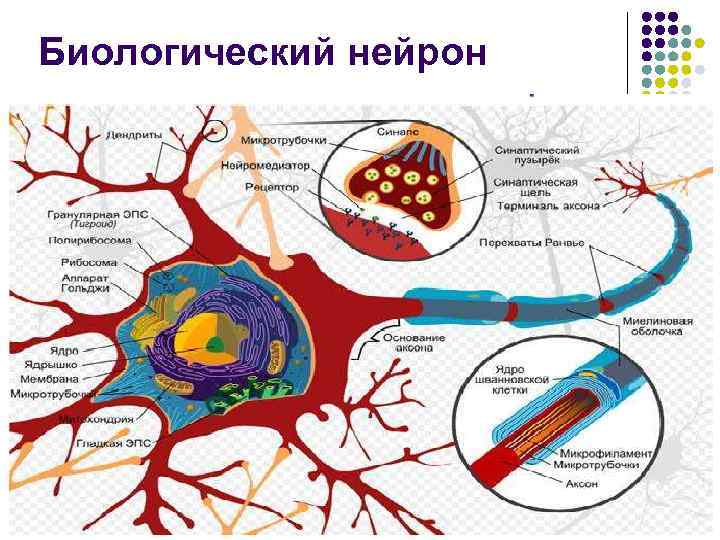
Биологический нейрон

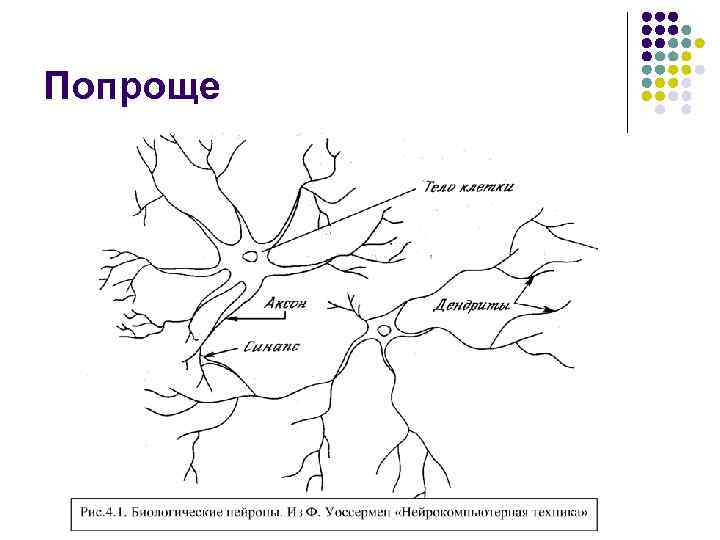
Попроще

Нейрофизиология

Формальная модель нейрона (Мак. Каллок, Питс)

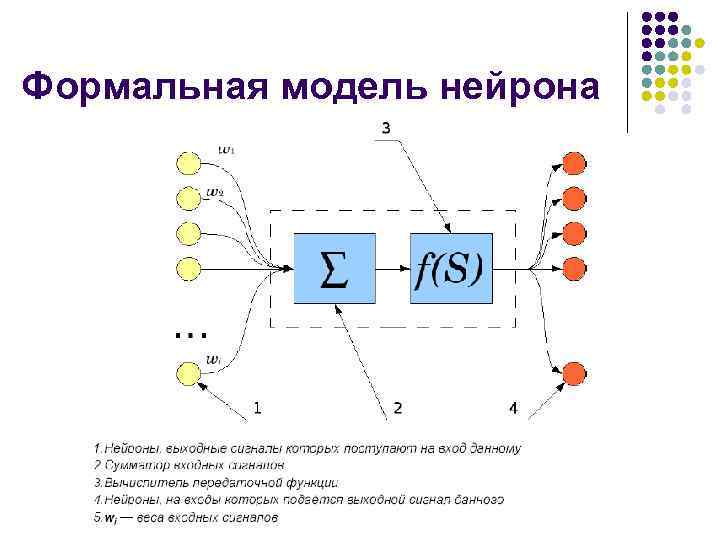
Формальная модель нейрона

Передаточная (активационная) функция

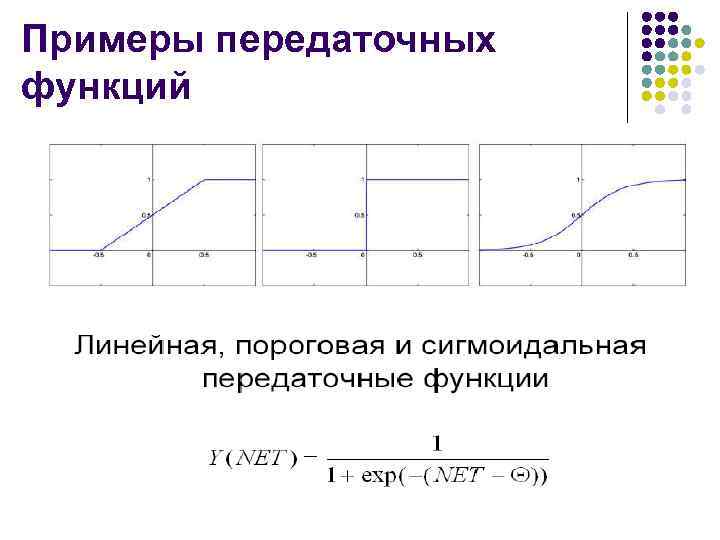
Примеры передаточных функций

Принцип работы искусственного нейрона

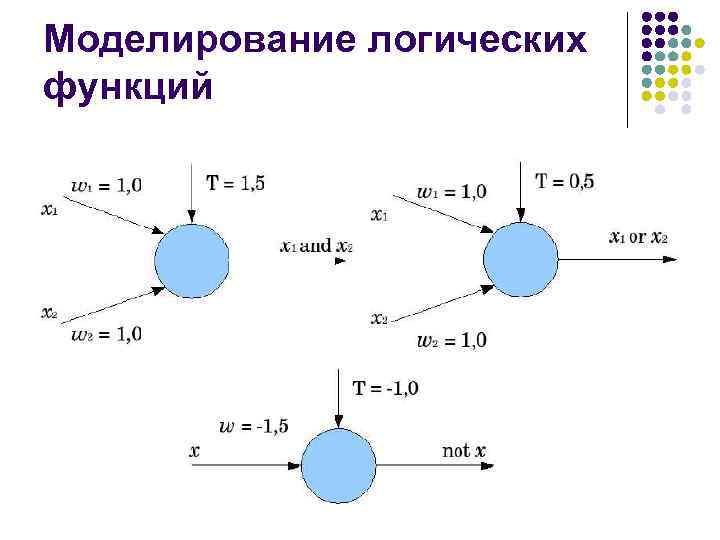
Моделирование логических функций

Применение

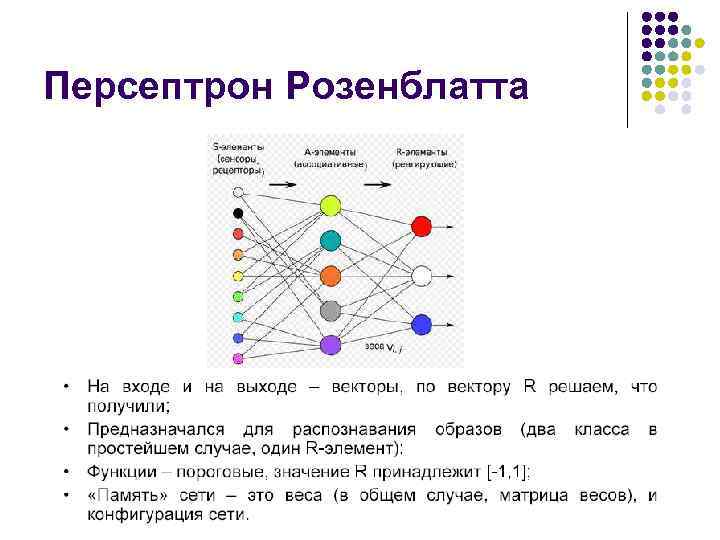
Персептрон Розенблатта

Классификация нейронов

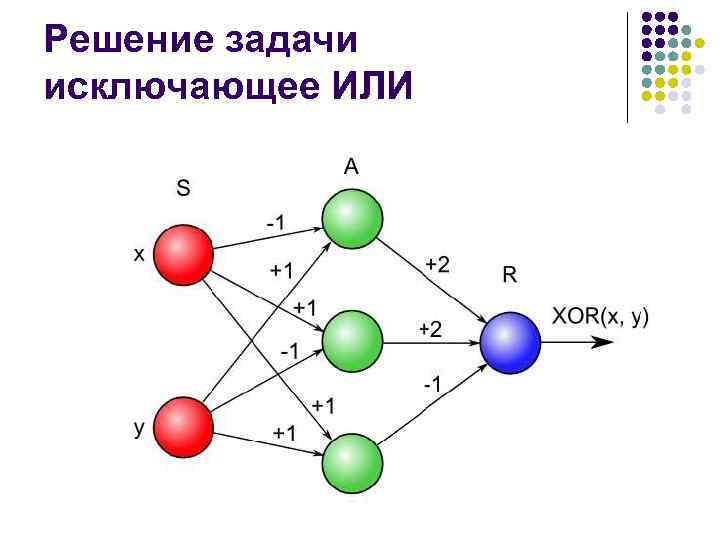
Решение задачи исключающее ИЛИ

Алгоритмы обучения

Дельта-правило

Алгоритм обратного распространения ошибки

Схема метода

Алгоритмы синтеза сетей

Правило обучения Хэбба Если два нейрона одновременно возбуждены, то сила связи между ними возрастает

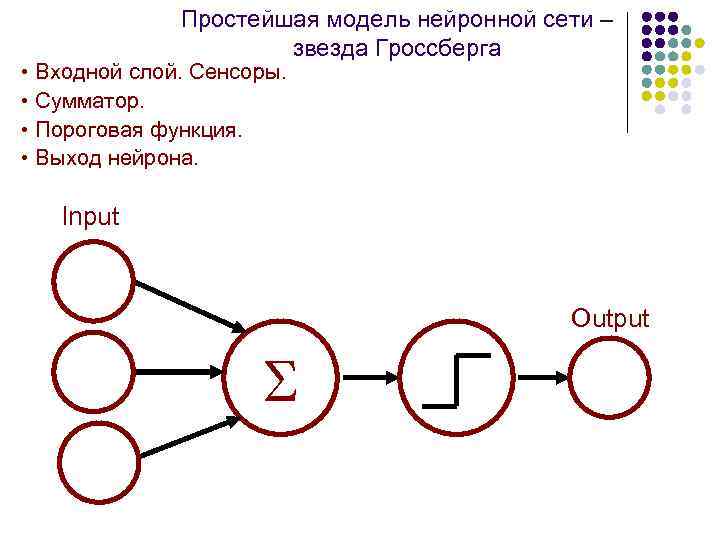
Простейшая модель нейронной сети – звезда Гроссберга • Входной слой. Сенсоры. • Сумматор. • Пороговая функция. • Выход нейрона. Input Output S

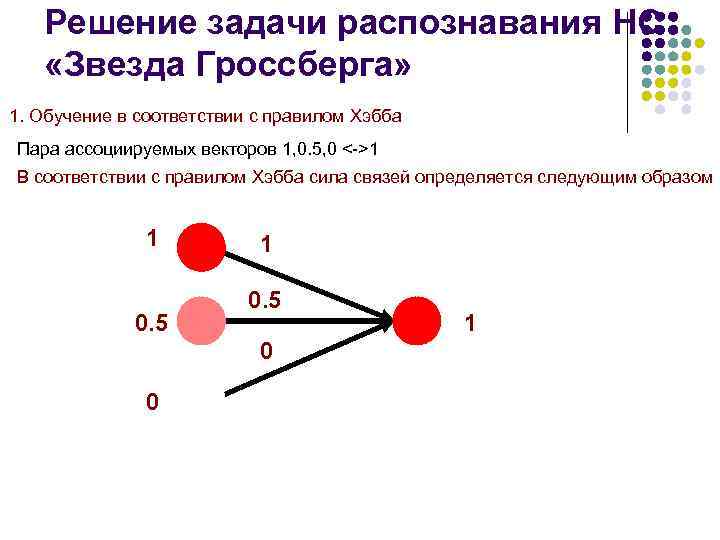
Решение задачи распознавания НС «Звезда Гроссберга» 1. Обучение в соответствии с правилом Хэбба Пара ассоциируемых векторов 1, 0. 5, 0 <->1 В соответствии с правилом Хэбба сила связей определяется следующим образом 1 0. 5 0 0 1

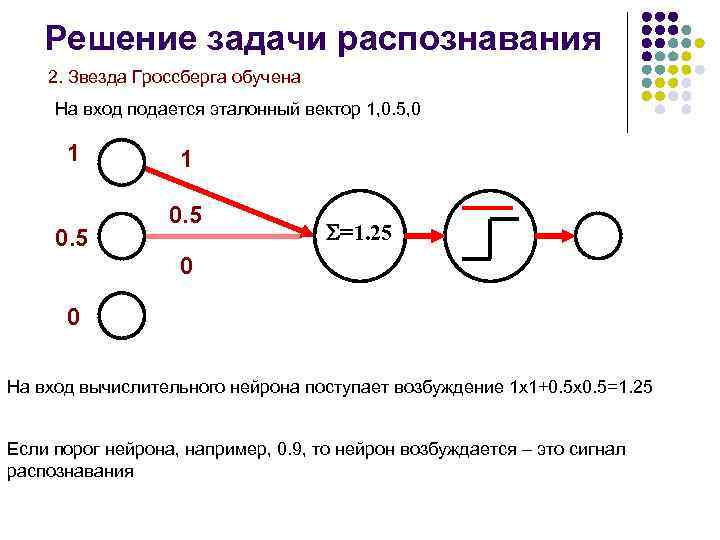
Решение задачи распознавания 2. Звезда Гроссберга обучена На вход подается эталонный вектор 1, 0. 5, 0 1 0. 5 =1. 25 0 0 На вход вычислительного нейрона поступает возбуждение 1 х1+0. 5 х0. 5=1. 25 Если порог нейрона, например, 0. 9, то нейрон возбуждается – это сигнал распознавания

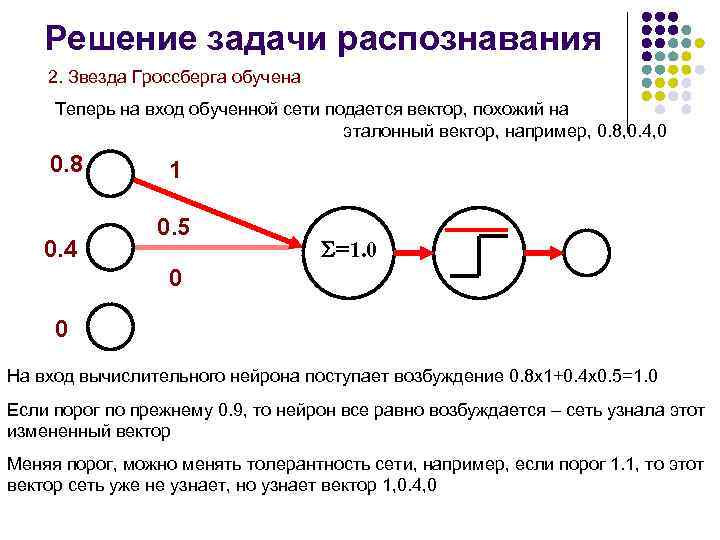
Решение задачи распознавания 2. Звезда Гроссберга обучена Теперь на вход обученной сети подается вектор, похожий на эталонный вектор, например, 0. 8, 0. 4, 0 0. 8 0. 4 1 0. 5 =1. 0 0 0 На вход вычислительного нейрона поступает возбуждение 0. 8 х1+0. 4 х0. 5=1. 0 Если порог по прежнему 0. 9, то нейрон все равно возбуждается – сеть узнала этот измененный вектор Меняя порог, можно менять толерантность сети, например, если порог 1. 1, то этот вектор сеть уже не узнает, но узнает вектор 1, 0. 4, 0

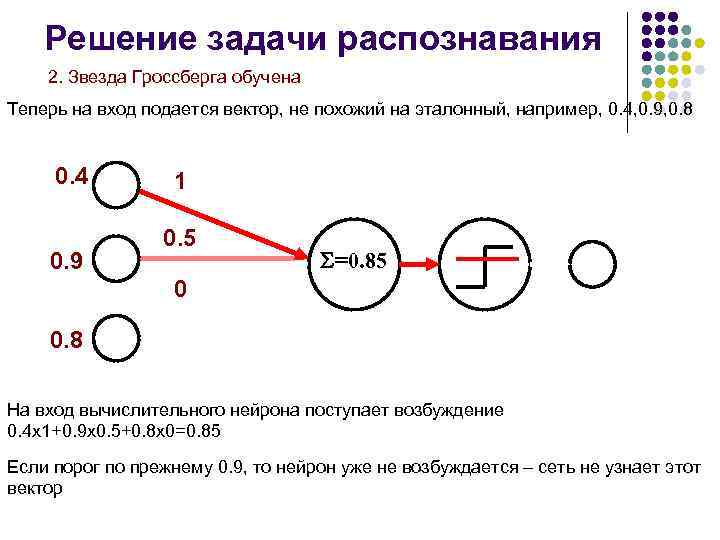
Решение задачи распознавания 2. Звезда Гроссберга обучена Теперь на вход подается вектор, не похожий на эталонный, например, 0. 4, 0. 9, 0. 8 0. 4 0. 9 1 0. 5 =0. 85 0 0. 8 На вход вычислительного нейрона поступает возбуждение 0. 4 х1+0. 9 х0. 5+0. 8 х0=0. 85 Если порог по прежнему 0. 9, то нейрон уже не возбуждается – сеть не узнает этот вектор

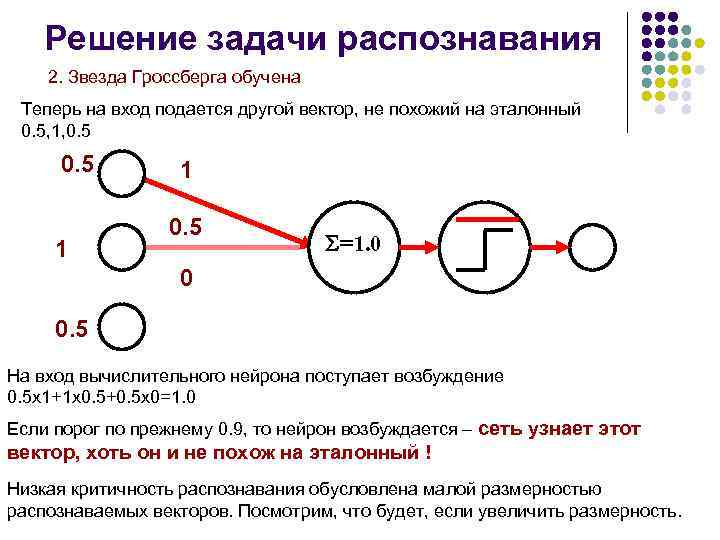
Решение задачи распознавания 2. Звезда Гроссберга обучена Теперь на вход подается другой вектор, не похожий на эталонный 0. 5, 1, 0. 5 1 1 0. 5 =1. 0 0 0. 5 На вход вычислительного нейрона поступает возбуждение 0. 5 х1+1 х0. 5+0. 5 х0=1. 0 Если порог по прежнему 0. 9, то нейрон возбуждается – сеть узнает этот вектор, хоть он и не похож на эталонный ! Низкая критичность распознавания обусловлена малой размерностью распознаваемых векторов. Посмотрим, что будет, если увеличить размерность.

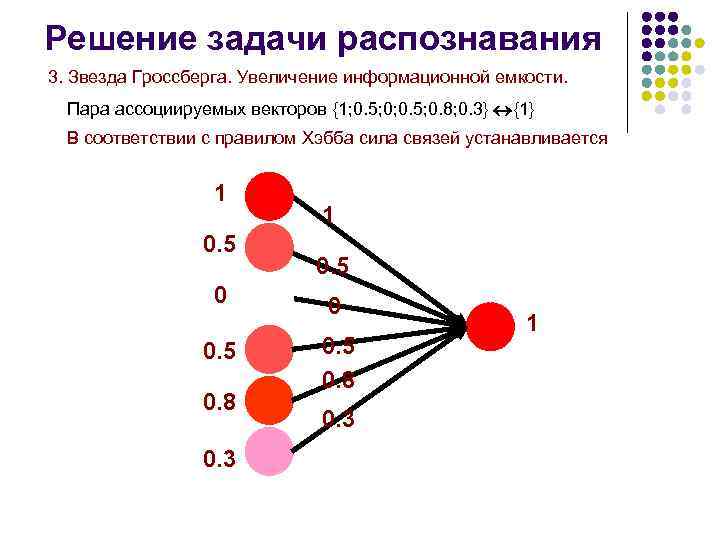
Решение задачи распознавания 3. Звезда Гроссберга. Увеличение информационной емкости. Пара ассоциируемых векторов {1; 0. 5; 0. 8; 0. 3} {1} В соответствии с правилом Хэбба сила связей устанавливается 1 0. 5 0. 8 0. 3 1

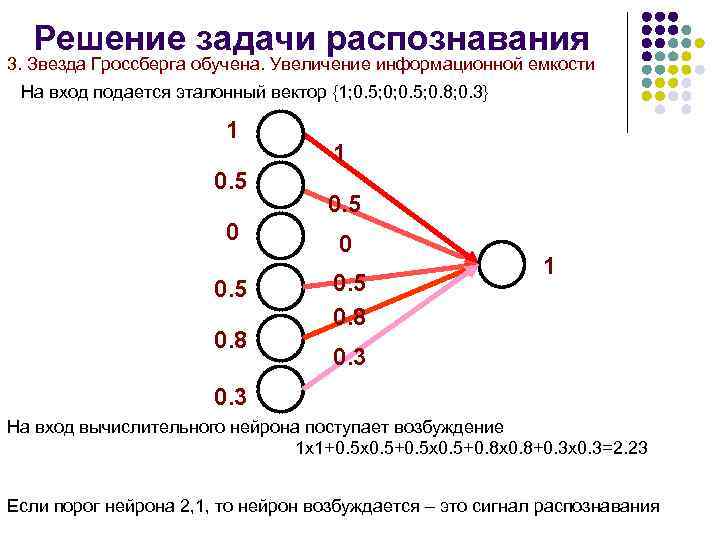
Решение задачи распознавания 3. Звезда Гроссберга обучена. Увеличение информационной емкости На вход подается эталонный вектор {1; 0. 5; 0. 8; 0. 3} 1 0. 5 0. 8 1 0. 3 На вход вычислительного нейрона поступает возбуждение 1 х1+0. 5 х0. 5+0. 8 х0. 8+0. 3 х0. 3=2. 23 Если порог нейрона 2, 1, то нейрон возбуждается – это сигнал распознавания

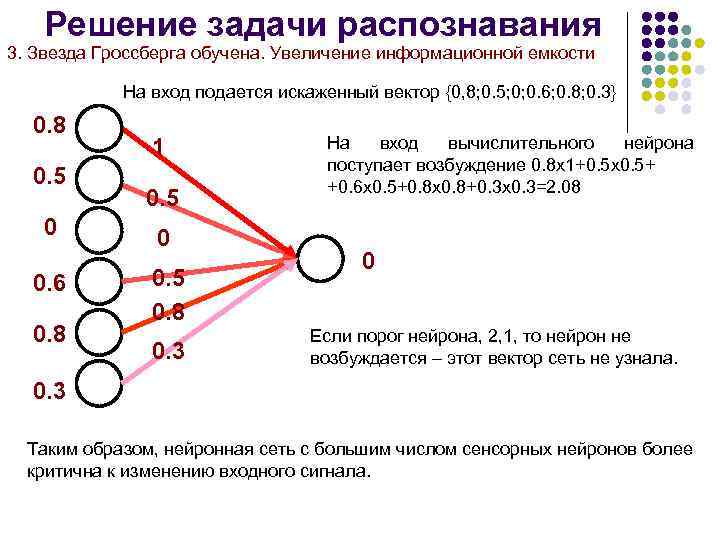
Решение задачи распознавания 3. Звезда Гроссберга обучена. Увеличение информационной емкости На вход подается искаженный вектор {0, 8; 0. 5; 0; 0. 6; 0. 8; 0. 3} 0. 8 0. 5 0 0. 6 0. 8 1 0. 5 0. 8 0. 3 На вход вычислительного нейрона поступает возбуждение 0. 8 х1+0. 5 х0. 5+ +0. 6 х0. 5+0. 8 х0. 8+0. 3 х0. 3=2. 08 0 Если порог нейрона, 2, 1, то нейрон не возбуждается – этот вектор сеть не узнала. 0. 3 Таким образом, нейронная сеть с большим числом сенсорных нейронов более критична к изменению входного сигнала.

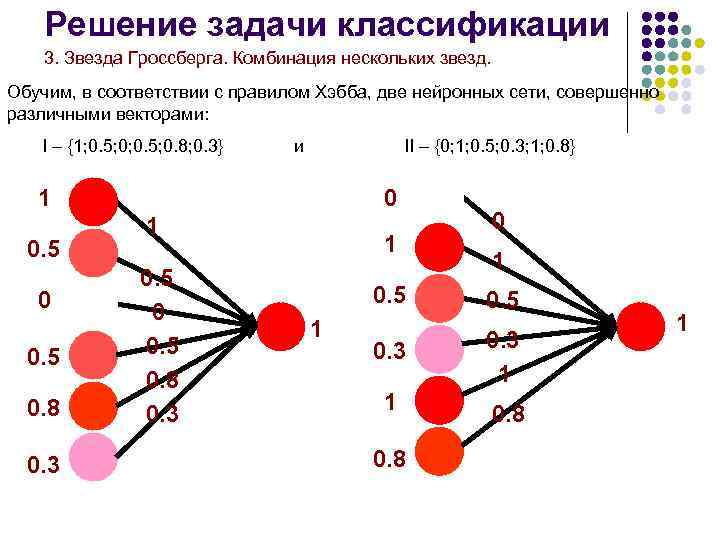
Решение задачи классификации 3. Звезда Гроссберга. Комбинация нескольких звезд. Обучим, в соответствии с правилом Хэбба, две нейронных сети, совершенно различными векторами: I – {1; 0. 5; 0. 8; 0. 3} и II – {0; 1; 0. 5; 0. 3; 1; 0. 8} 1 0. 5 0. 8 0. 3 0 1 0. 5 0. 8 0. 3 1 0. 5 0. 3 1 1 0. 8 1

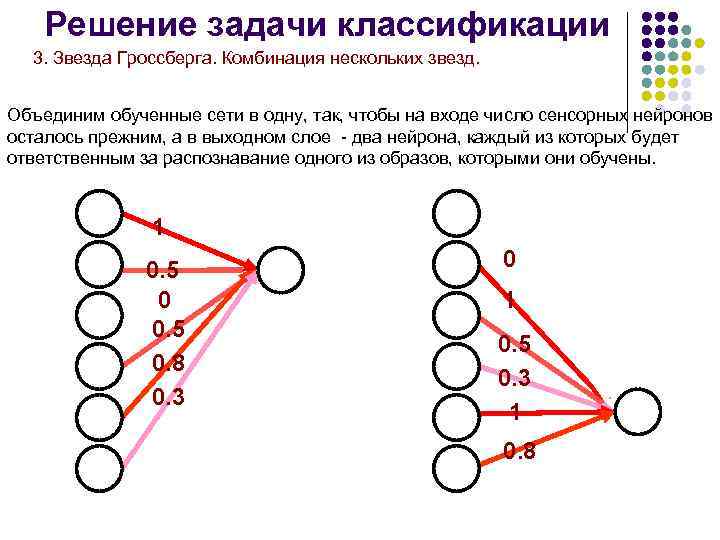
Решение задачи классификации 3. Звезда Гроссберга. Комбинация нескольких звезд. Объединим обученные сети в одну, так, чтобы на входе число сенсорных нейронов осталось прежним, а в выходном слое - два нейрона, каждый из которых будет ответственным за распознавание одного из образов, которыми они обучены. 1 0. 5 0. 8 0. 3 0 1 0. 5 0. 3 1 0. 8

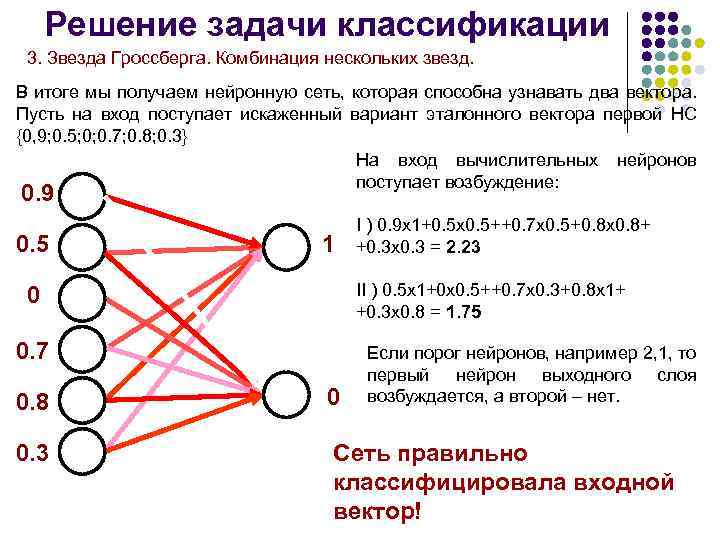
Решение задачи классификации 3. Звезда Гроссберга. Комбинация нескольких звезд. В итоге мы получаем нейронную сеть, которая способна узнавать два вектора. Пусть на вход поступает искаженный вариант эталонного вектора первой НС {0, 9; 0. 5; 0; 0. 7; 0. 8; 0. 3} На вход вычислительных нейронов поступает возбуждение: 0. 9 0. 5 1 I ) 0. 9 х1+0. 5 х0. 5++0. 7 х0. 5+0. 8 х0. 8+ +0. 3 х0. 3 = 2. 23 II ) 0. 5 х1+0 х0. 5++0. 7 х0. 3+0. 8 х1+ +0. 3 х0. 8 = 1. 75 0 0. 7 Если порог нейронов, например 2, 1, то первый нейрон выходного слоя возбуждается, а второй – нет. 0. 8 0 0. 3 Сеть правильно классифицировала входной вектор!

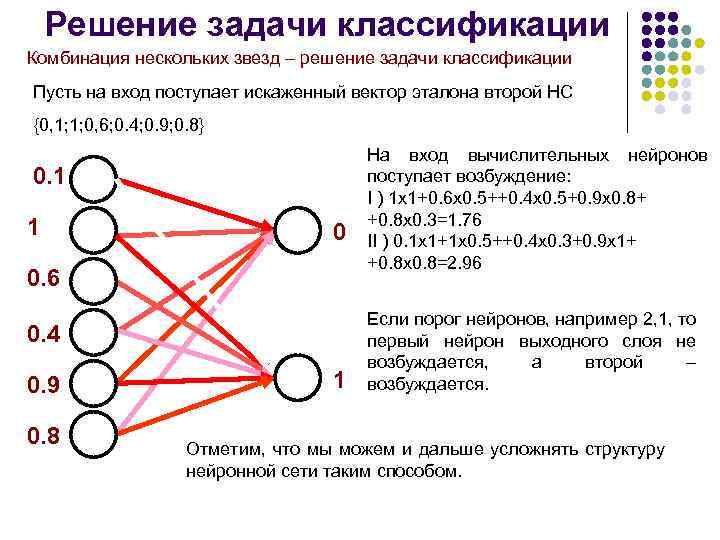
Решение задачи классификации Комбинация нескольких звезд – решение задачи классификации Пусть на вход поступает искаженный вектор эталона второй НС {0, 1; 1; 0, 6; 0. 4; 0. 9; 0. 8} 0. 1 1 0 0. 6 0. 4 0. 9 0. 8 1 На вход вычислительных нейронов поступает возбуждение: I ) 1 х1+0. 6 х0. 5++0. 4 х0. 5+0. 9 х0. 8+ +0. 8 х0. 3=1. 76 II ) 0. 1 х1+1 х0. 5++0. 4 х0. 3+0. 9 х1+ +0. 8 х0. 8=2. 96 Если порог нейронов, например 2, 1, то первый нейрон выходного слоя не возбуждается, а второй – возбуждается. Отметим, что мы можем и дальше усложнять структуру нейронной сети таким способом.