ISAMA 2004 Chicago K 12 and the Genus-6

ISAMA 2004, Chicago K 12 and the Genus-6 Tiffany Lamp Carlo H. Séquin and Ling Xiao EECS Computer Science Division University of California, Berkeley

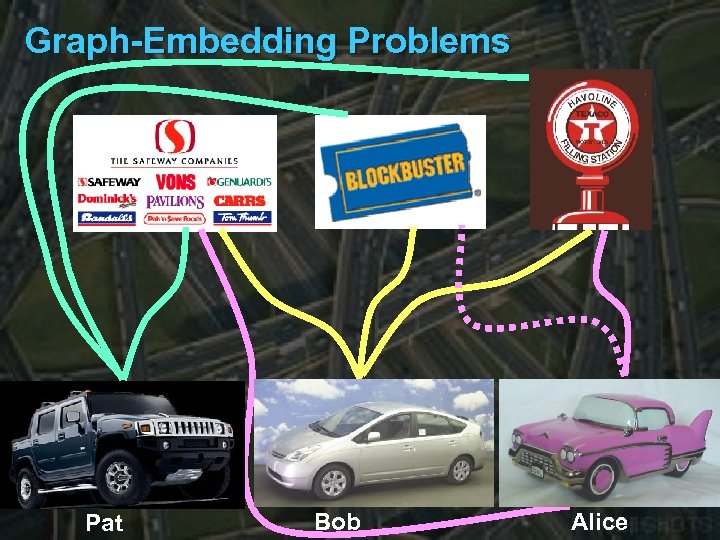Graph-Embedding Problems Pat Bob Alice

On a Ringworld (Torus) this is No Problem ! Alice Bob Pat Harry

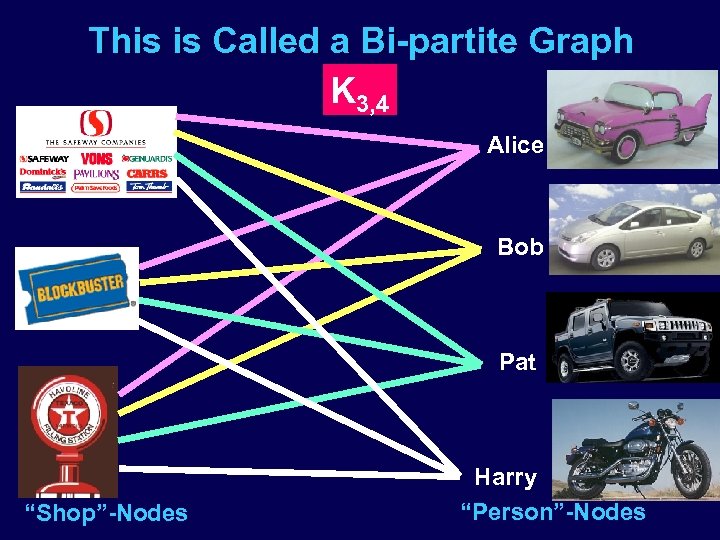This is Called a Bi-partite Graph K 3, 4 Alice Bob Pat “Shop”-Nodes Harry “Person”-Nodes

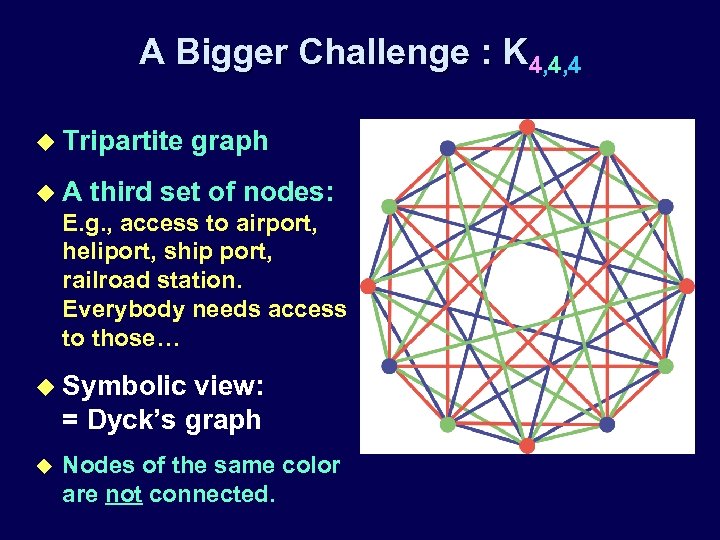A Bigger Challenge : K 4, 4, 4 u Tripartite u. A graph third set of nodes: E. g. , access to airport, heliport, ship port, railroad station. Everybody needs access to those… u Symbolic view: = Dyck’s graph u Nodes of the same color are not connected.

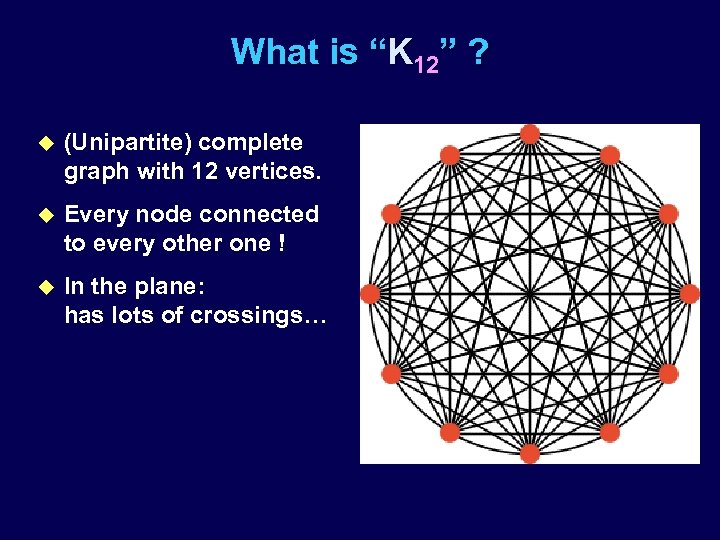What is “K 12” ? u (Unipartite) complete graph with 12 vertices. u Every node connected to every other one ! u In the plane: has lots of crossings…

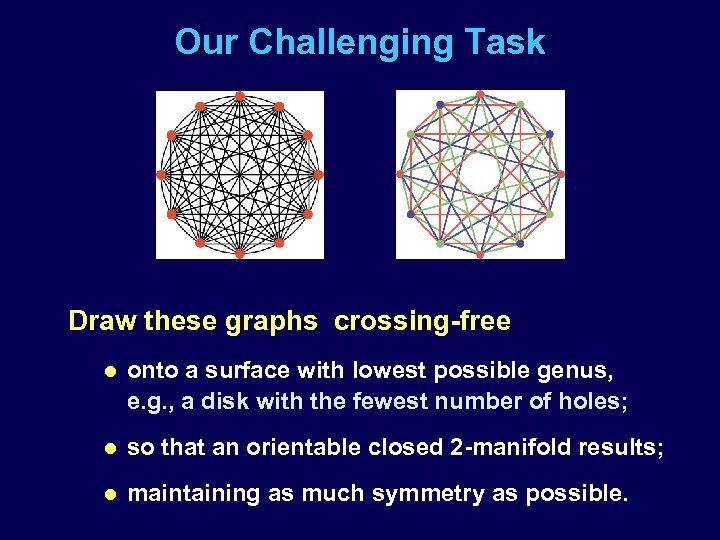Our Challenging Task Draw these graphs crossing-free l onto a surface with lowest possible genus, e. g. , a disk with the fewest number of holes; l so that an orientable closed 2 -manifold results; l maintaining as much symmetry as possible.

Not Just Stringing Wires in 3 D … u Icosahedron has 12 vertices in a nice symmetrical arrangement; -- let’s just connect those … u But we want graph embedded in a (orientable) surface !

Mapping Graph K 12 onto a Surface (i. e. , an orientable 2 -manifold) u Draw complete graph with 12 nodes (vertices) u Graph has 66 edges u Orientable 2 -manifold has 44 triangular facets u # Edges – # Vertices – # Faces + 2 = 2*Genus u 66 – 12 – 44 + 2 = 12 (=border between 2 facets) Genus = 6 Now make a (nice) model of that ! There are 59 topologically different ways in which this can be done ! [Altshuler et al. 96]

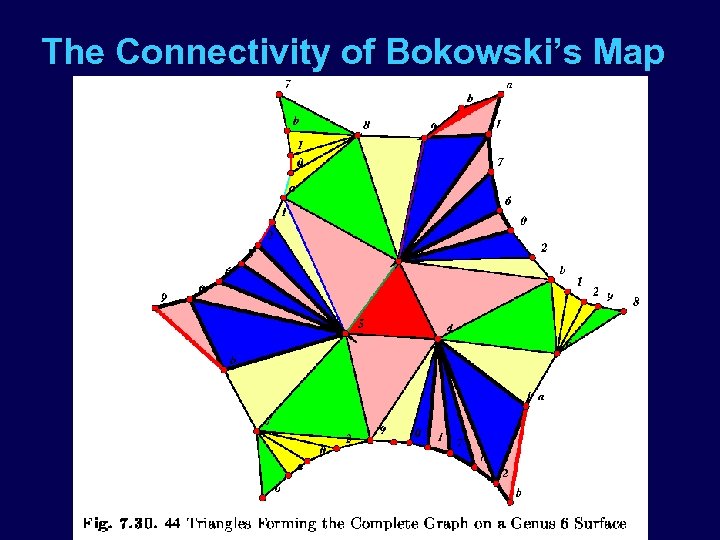The Connectivity of Bokowski’s Map

Prof. Bokowski’s Goose-Neck Model

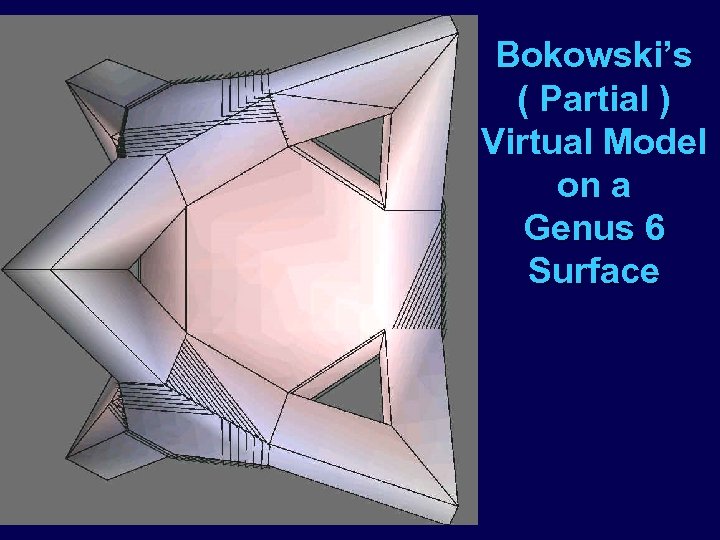Bokowski’s ( Partial ) Virtual Model on a Genus 6 Surface

My First Model u Find highest-symmetry genus-6 surface, u with “convenient” handles to route edges.

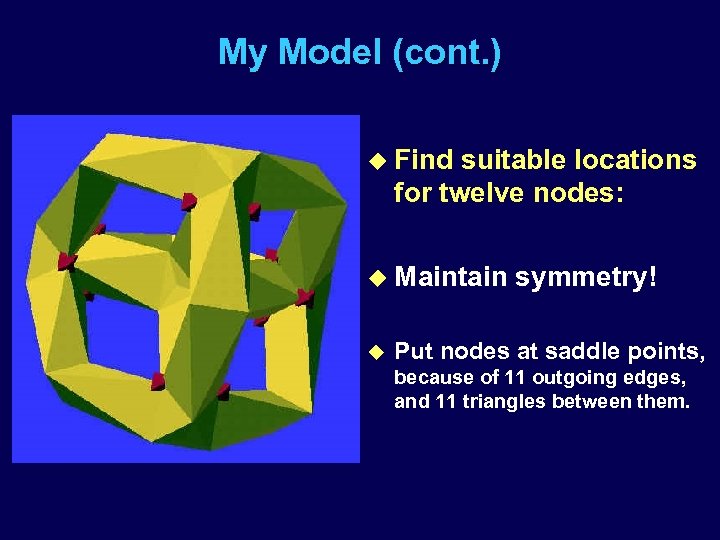My Model (cont. ) u Find suitable locations for twelve nodes: u Maintain u symmetry! Put nodes at saddle points, because of 11 outgoing edges, and 11 triangles between them.

My Model (3) u Now need to place 66 edges: u Use trial and error. u Need u CAD a 3 D model ! model much later. . .

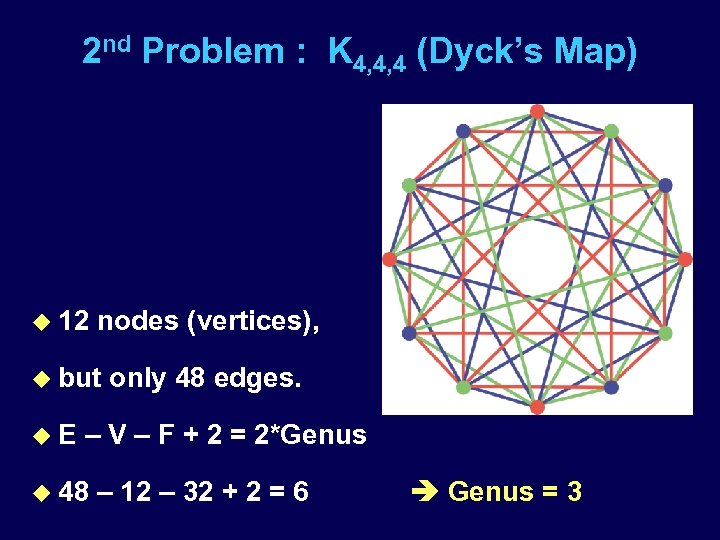2 nd Problem : K 4, 4, 4 (Dyck’s Map) u 12 nodes (vertices), u but u. E only 48 edges. – V – F + 2 = 2*Genus u 48 – 12 – 32 + 2 = 6 Genus = 3

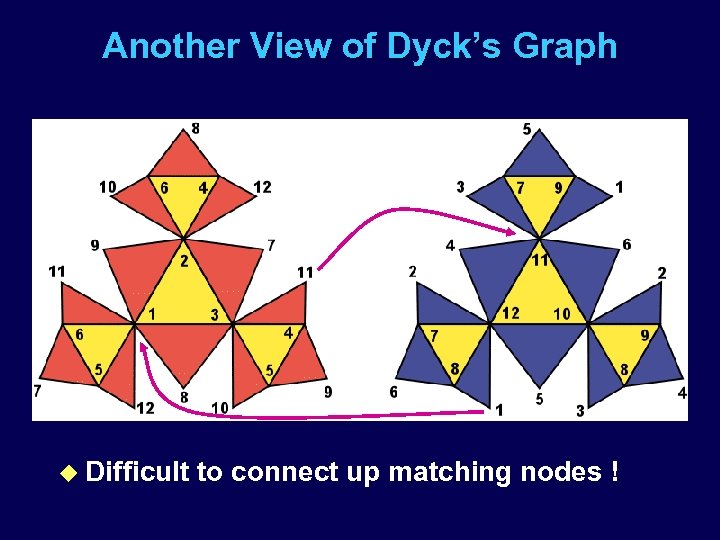Another View of Dyck’s Graph u Difficult to connect up matching nodes !

Folding It into a Self-intersecting Polyhedron

Towards a 3 D Model u Find highest-symmetry genus-3 surface: Klein Surface (tetrahedral frame).

Find Locations for Nodes u Actually harder than in previous example, not all nodes connected to one another. (Every node has 3 that it is not connected to. ) u Place them so that the missing edges do not break the symmetry: u Inside and outside on each tetra-arm. u Do not connect the nodes that lie on the same symmetry axis (same color) (or this one).

A First Physical Model u Edges of graph should be nice, smooth curves. Quickest way to get a model: Painting a physical object.

Geodesic Line Between 2 Points T S u Connecting two given points with the shortest geodesic line on a high-genus surface is an NP-hard problem.

“Pseudo Geodesics” u Need more control than geodesics can offer. u Want to space the departing curves from a vertex more evenly, avoid very acute angles. u Need control over starting and ending tangent directions (like Hermite spline).

LVC Curves (instead of MVC) u Curves with linearly varying curvature have two degrees of freedom: k. A k. B, u Allows to set two additional parameters, i. e. , the start / ending tangent directions. CURVATURE k. B ARC-LENGTH k. A B A

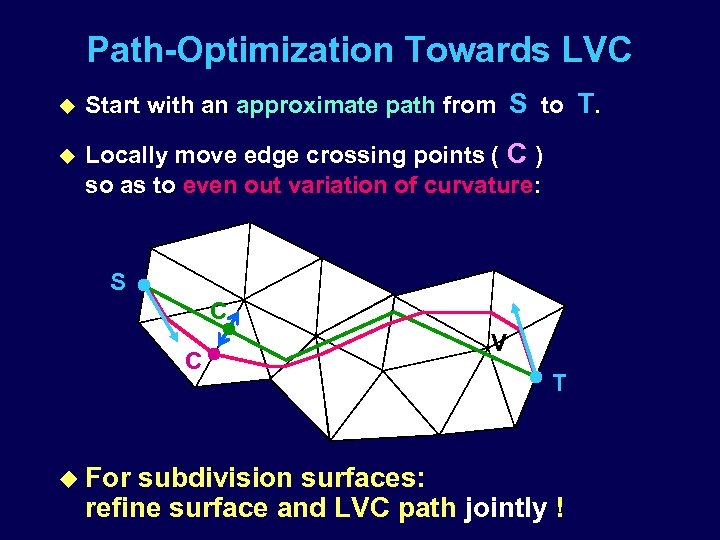Path-Optimization Towards LVC u Start with an approximate path from S to T. u Locally move edge crossing points ( C ) so as to even out variation of curvature: S C C u For V T subdivision surfaces: refine surface and LVC path jointly !

K 4, 4, 4 on a Genus-3 Surface LVC on subdivision surface – Graph edges enhanced

K 12 on a Genus-6 Surface

3 D Color Printer (Z Corporation)

Cleaning up a 3 D Color Part

Finishing of 3 D Color Parts Infiltrate Alkyl Cyanoacrylane Ester = “super-glue” to harden parts and to intensify colors.

Genus-6 Regular Map

Genus-6 Regular Map

“Genus-6 Kandinsky”

Manually Over-painted Genus-6 Model

Bokowski’s Genus-6 Surface

Tiffany Lamps (L. C. Tiffany 1848 – 1933)

Tiffany Lamps with Other Shapes ? Globe ? -- or Torus ? Certainly nothing of higher genus !

Back to the Virtual Genus-3 Map Define color panels to be transparent !

A Virtual Genus-3 Tiffany Lamp

Light Cast by Genus-3 “Tiffany Lamp” Rendered with “Radiance” Ray-Tracer (12 hours)

Virtual Genus-6 Map

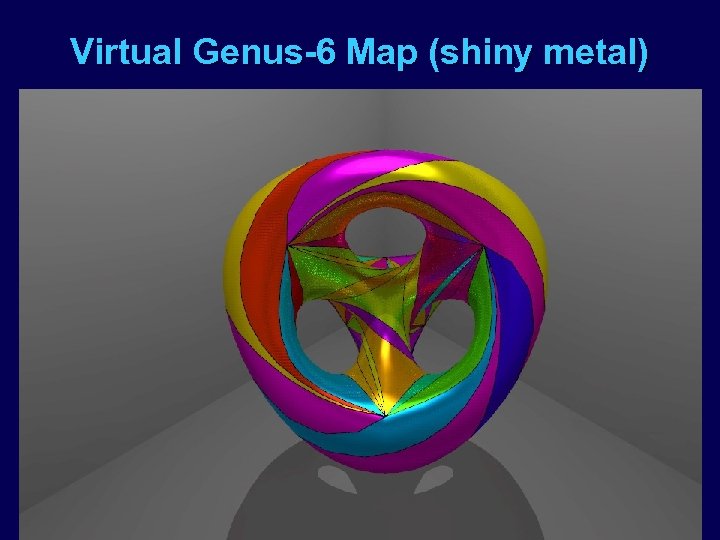Virtual Genus-6 Map (shiny metal)

Light Field of Genus-6 Tiffany Lamp