Is solving harder than checking Oded Goldreich Weizmann

Is solving harder than checking? Oded Goldreich Weizmann institute of science

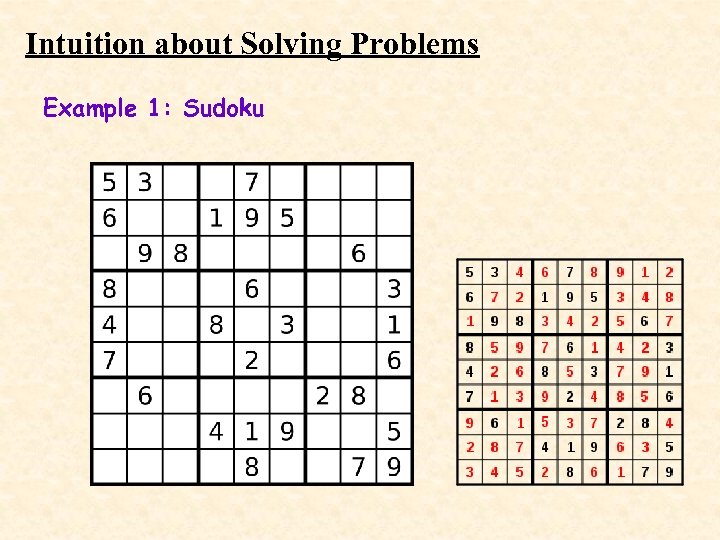Intuition about Solving Problems Example 1: Sudoku

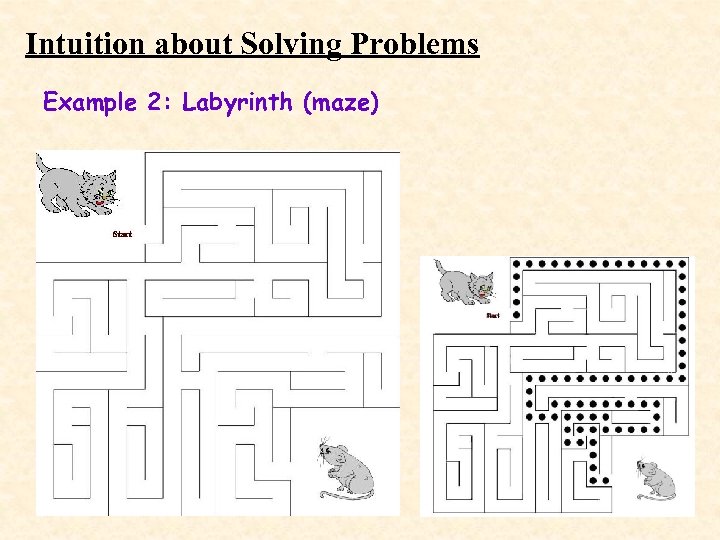Intuition about Solving Problems Example 2: Labyrinth (maze)

Intuition about Solving Problems Example 3: Jigsaw puzzle

Math Problems Example 1: Factoring integers 5561 = 67 83 638257 = 787 811 61512881 = 6917 8893

Math Problems Example 2: Solving a system of linear (or quadratic) equations 2 x + 3 y z x y + 3 z 3 x + 2 y + z = 9 = 4 x = 1 = y = 2 0 z = 1 2 x 2 + 3 xy z x y 2 = 0 + 3 yz = 5 3 x + 2 xy +2 xz = 3 x = 1 y = 1 z = 1

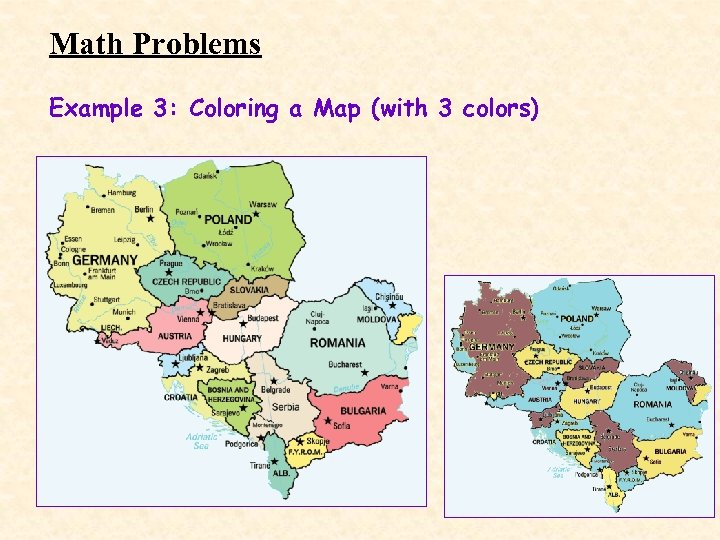Math Problems Example 3: Coloring a Map (with 3 colors)

Math Problems Example 4: Traveling Salesperson Problem (TSP) Given the pair-wise distances between 12 cities and a total distance bound, find a tour that visits all 12 cities and covers a total distance that does not exceed the bound. Location Jerus alem Tel. Haifa Aviv Tiberi as Beer Sheba Eilat Jerusalem -- 58 151 152 81 309 Tel-Aviv 58 -- 95 134 105 346 Haifa 151 95 -- 69 197 438 Tiberias 152 134 69 -- 233 405 Beer Sheba 81 105 197 233 -- 241 Eilat 309 346 438 405 241 -- Example 5: Knapsack Given a sequence of 20 integers and a target T, find a subset of the integers that sums-up to T.

A common feature: Easy to check correctness The fact that it is easy to check correctness of candidate solutions yields an obvious (but slow) way of finding solutions to all problems, called exhaustive search: Just try all potential solutions and check the correctness of each of them, halting with a correct solution once it is found.

Exhaustive search: an obvious (but slow) way of finding solutions to all problems Trying all potential solutions, we find a correct one once it is tried. Example 1: Sudoku (with 50/81 entries missing). 950 possibilities. Example 2: Labyrinth (with 20 junction/choices). 220 possibilities. Example 3: 3 -coloring a map (with 20 countries). 320 possibilities. Example 4: Factoring 8 -digit integers. 10000 possibilities. (When factoring 200 -digit integers, there are 10100 possibilities!) Example 5: TSP (with 12 cities). 11! = 39, 916, 800 possibilities.

Are there better ways to find solutions? (That is, faster than by exhaustive search) Example 1: Solving systems of linear equations. YES! Example 2: Solving systems of quadratic equations. (prob. ) NO! Example 3: 3 -coloring a (3 -colorable) map. (prob. ) NO! Example 4: 2 -coloring a (2 -colorable) map. YES! Example 5: TSP (traveling salesperson). Example 6: Factoring integers. (prob. ) NO! (prob. ) NO.

Formulation: what do we mean by a search problem? A problem is not a specific instance (e. g. , a specific Sudoko puzzle), but rather the general form/class/type (e. g. , Sudoku). A search problem consists of an infinite (or huge) set of instances and a concise/simple specification of valid solutions. Example 1 (Sudoku): An instance is any 9 -by-9 rectangle partially filled with single digits, and a valid solution is an assignment of digits to the empty cells such that … Example 2 (coloring maps): An instance is a 3 -colorable map, and a valid solution is a 3 -coloring of the areas such that no two adjacent areas are assigned the same color. Example 3 (solving systems of equations): An instance is any system of (linear or quadratic) equations, and a solution is an assignment of numbers to the variables such that …

Formulation: search problems (more examples) A search problem consists of an infinite (or huge) set of instances and a concise/simple specification of valid solutions. Example 4 (TSP): An instance is any n-by-n matrix of distances among n cities and a bound L, and a valid solution is a tour that passes all n cities and has total length at most L. Example 5 (Factoring): An instance is a composite number N, and a valid solution is a pair of numbers (P, Q) such that N=P Q. Example 6 (Knapsack): An instance is any sequence of numbers N 1, N 2, …, Nn, T, and a solution is a subset of the n first numbers that sums-up to T (i. e. , a set I such that ∑i INi = T).

The P-vs-NP Question (version 1: search problems) “P” = All search problems that can be solved efficiently; that is, there exists an efficient procedure that, when given an instance of the problem, finds a valid solution to that instance (or indicates that none exists). “NP” = All search problems for which valid solutions can be efficiently recognized; that is, there exists an efficient procedure that, when given an instance-solution pair, determines whether or not the solution is valid. It is widely believed that there are problems in NP P. For example: 3 -Coloring, TSP, Knapsack, Solve-Quad-Equations, and also Factoring.

Decision problems (a formulation) Again, a problem is not a specific instance (e. g. , a specific Sudoko puzzle), but rather the general form/class/type (e. g. , Sudoku). A decision problem consists of an infinite (or huge) set of instances and a concise/simple specification of YES-instnaces (a set of instances having a “desired” property). A generic example (having solutions w. r. t a search problem): An instance is an instance of a search problem, and the question is whether this instance has a solution. Example 1 (Sudoku): An instance is any 9 -by-9 rectangle partially filled with single digits, and the question is whether it can be augmented such that … Example 2 (coloring maps): An instance is a map, and the question is whether it is 3 -colrable (i. e. , whethere exists a 3 -coloring of the areas such that no two adjacent areas are assigned the same color).

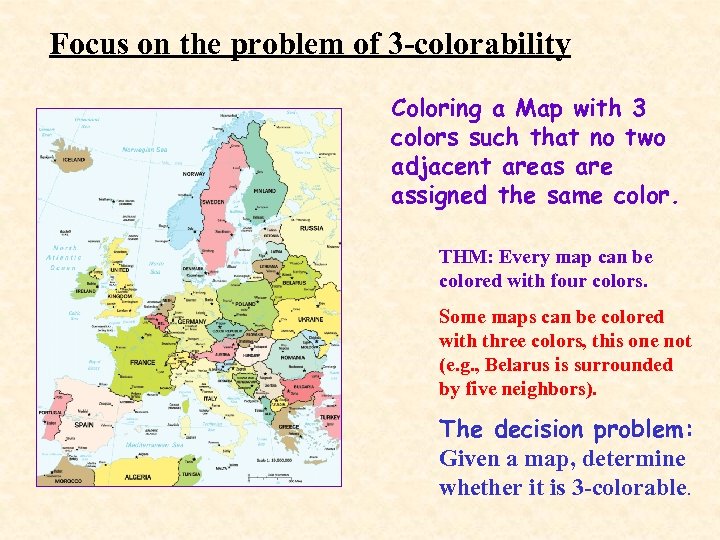Focus on the problem of 3 -colorability Coloring a Map with 3 colors such that no two adjacent areas are assigned the same color. THM: Every map can be colored with four colors. Some maps can be colored with three colors, this one not (e. g. , Belarus is surrounded by five neighbors). The decision problem: Given a map, determine whether it is 3 -colorable.

The P-vs-NP Question (version 2: decision problems) P = All decision problems that can be solved efficiently; that is, there exists an efficient procedure that, when given an instance of the problem, determines whether it is a YES-instance. NP = All decision problems for which each YES-instance has an efficiently verifiable certificate; that is, there exists an efficient procedure that, when given an instancecertificate pair, determines whether or not the certificate is valid. It is widely believed that there are problems in NP P. For example: 3 -Coloring, TSP, Knapsack, Solve-Quad-Equations.

Showing that an NP-problem is not in P P = All decision problems that can be solved efficiently; that is, there exists an efficient procedure that, when given an instance of the problem, determines whether it is a YES-instance. NP = All decision problems for which each YES-instance has an efficiently verifiable certificate; that is, there exists an efficient procedure that, when given an instance-certificate pair, determines whether or not the certificate is valid. Assuming that P NP (but not knowing it for a fact), can we tell whether a specific problem is in NP-P? We can only hope for a conditional result (i. e. , cond’ed on P NP). We say that an NP-problem is NP-complete if the ability to efficiently solve it implies the ability to efficiently solve any problem in NP. P NP NP-complete problems are hard to solve. Thus, showing that a problem is NP-complete will do. (For example: 3 -Coloring, TSP, Knapsack, Solve-Quad-Equations. )

Universal problems (NP-completeness) A problem in NP is called NP-complete if the ability to efficiently solve it implies the ability to efficiently solve any problem in NP. Recall: P NP NP-complete problems are hard to solve. How can NP-complete problems possibly exist? (Let alone how can we prove that they exist? ) Indeed, a good question to be answered next. Still, let us state (as a fact/theorem) that 3 -Coloring, TSP, Knapsack, Solve-Quad-Equations are all NP-complete. P = All decision problems that can be solved efficiently; that is, there exists an efficient procedure that, when given an instance of the problem, determines whether it is a YES-instance. NP = All decision problems for which each YES-instance has an efficiently verifiable certificate; that is, there exists an efficient procedure that, when given an instance-certificate pair, determines whether or not the certificate is valid.

Universal problems (NP-completeness) [continued] A (decision) problem C in NP is called NP-complete if the ability to efficiently solve it implies the ability to efficiently solve any (decision) problem D in NP. How can NP-complete problems possibly exist? (Let alone how can we prove that they exist? ) Idea: An efficient transformation of instances of (any NP) problem D into instances of problem C such that YES-instances are mapped to YES-instances (and NO-instances are mapped to NO-instances). For example: 3 -Coloring, TSP, Knapsack, Solve-Quad-Equations are all NP-complete. Instances, say, of FACTORING (in NP) can be mapped to any of them.

Universal problems (NP-completeness) [2 nd cont. ] A (decision) problem C in NP is called NP-complete if the ability to efficiently solve it implies the ability to efficiently solve any (decision) problem D in NP. Shown via an efficient transformation of instances of (any NP) problem D into instances of problem C such that YES-instances are mapped to YES-instances (and NO-instances are mapped to NO-instances). D YES NO (e. g. , Factor) YES NO C (e. g. , 3 Color)

the end The slides of this talk are available at http: //www. wisdom. weizmann. ac. il/~oded/T/p-vs-np. ppt A related textbook is available at http: //www. wisdom. weizmann. ac. il/~oded/bc-book. html