IS 2150 TEL 2810 Introduction to Security

IS 2150 / TEL 2810 Introduction to Security Key Management October 26, 2006 Lecture 7 1

Issues n Authentication and distribution of keys n n n Session key Key exchange protocols Kerberos Mechanisms to bind an identity to a key Generation, maintenance and revoking of keys 2

Notation n X Y : { Z || W } k. X, Y n n A T : { Z } k. A || { W } k. A, T n n X sends Y the message produced by concatenating Z and W enciphered by key k. X, Y, which is shared by users X and Y A sends T a message consisting of the concatenation of Z enciphered using k. A, A’s key, and W enciphered using k. A, T, the key shared by A and T r 1, r 2 nonces (nonrepeating random numbers) 3

Session, Interchange Keys n Alice wants to send a message m to Bob n n Assume public key encryption Alice generates a random cryptographic key ks and uses it to encipher m n n n She enciphers ks with Bob’s public key k. B n n n To be used for this message only Called a session key k. B enciphers all session keys Alice uses to communicate with Bob Called an interchange key Alice sends { m } ks { ks } k. B 4

Benefits n Limits amount of traffic enciphered with single key n n n Standard practice, to decrease the amount of traffic an attacker can obtain Makes replay attack less effective Prevents some attacks n n n Example: Alice will send Bob message that is either “BUY” or “SELL”. Eve computes possible ciphertexts {“BUY”} k. B and {“SELL”} k. B. Eve intercepts enciphered message, compares, and gets plaintext at once 5

Key Exchange Algorithms n n Goal: Alice, Bob use a shared key to communicate secretly Criteria n Key cannot be sent in clear n n Attacker can listen in Key can be sent enciphered, or derived from exchanged data plus data not known to an eavesdropper Alice, Bob may trust third party All cryptosystems, protocols publicly known n n Only secret data is the keys, ancillary information known only to Alice and Bob needed to derive keys Anything transmitted is assumed known to attacker 6

Classical Key Exchange n How do Alice, Bob begin? n n Assume trusted third party, Cathy n n n Alice can’t send it to Bob in the clear! Alice and Cathy share secret key k. A Bob and Cathy share secret key k. B Use this to exchange shared key ks 7

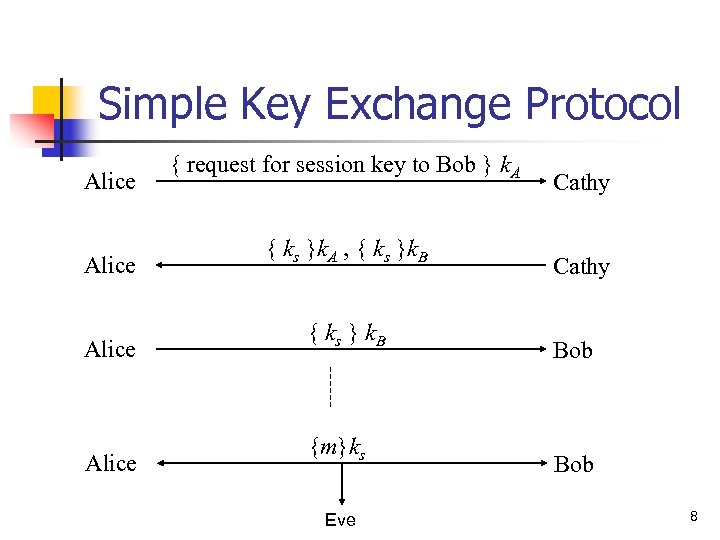Simple Key Exchange Protocol Alice { request for session key to Bob } k. A { ks }k. A , { ks }k. B { ks } k. B {m}ks Eve Cathy Bob 8

Problems n How does Bob know he is talking to Alice? n n n Replay attack: Eve records message from Alice to Bob, later replays it; Bob may think he’s talking to Alice, but he isn’t Session key reuse: Eve replays message from Alice to Bob, so Bob re-uses session key Protocols must provide authentication and defense against replay 9

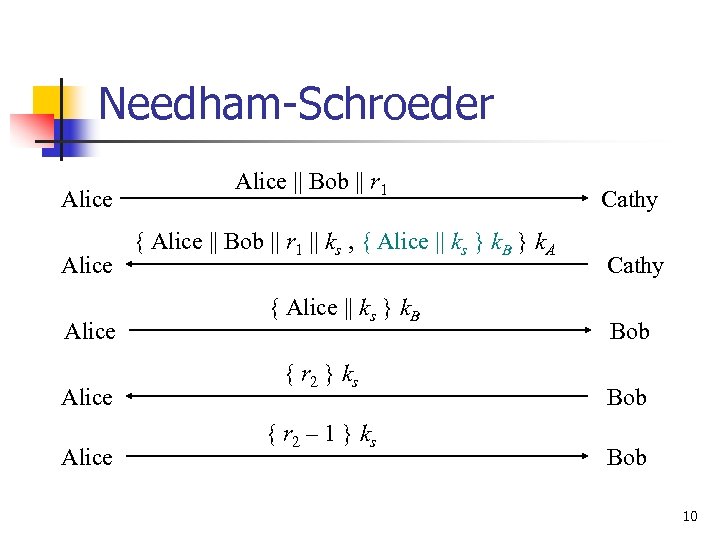Needham-Schroeder Alice Alice || Bob || r 1 { Alice || Bob || r 1 || ks , { Alice || ks } k. B } k. A { Alice || ks } k. B { r 2 } k s { r 2 – 1 } k s Cathy Bob Bob 10

Argument: Alice talking to Bob n Second message n Enciphered using key only she, Cathy know n n Response to first message n n So Cathy enciphered it As r 1 in it matches r 1 in first message Third message n Alice knows only Bob can read it n n As only Bob can derive session key from message Any messages enciphered with that key are from Bob 11

Argument: Bob talking to Alice n Third message n Enciphered using key only he, Cathy know n n Names Alice, session key n n So Cathy enciphered it Cathy provided session key, says Alice is other party Fourth message n Uses session key to determine if it is replay from Eve n n If not, Alice will respond correctly in fifth message If so, Eve can’t decipher r 2 and so can’t respond, or responds incorrectly 12

Problem with Needham-Schroeder n n Assumption: all keys are secret Question: suppose Eve can obtain session key. How does that affect protocol? n Eve Eve In what follows, Eve knows ks { Alice || ks } k. B { r 3 } k s { r 3 – 1 } k s [Replay] [Eve intercepts] Bob Bob 13

Solution: Denning-Sacco Modification n n In protocol above, Eve impersonates Alice Problem: replay in third step n n Solution: use time stamp T to detect replay n n First in previous slide Needs synchronized clocks Weakness: if clocks not synchronized, may either reject valid messages or accept replays n n Parties with either slow or fast clocks vulnerable to replay Resetting clock does not eliminate vulnerability 14

Needham-Schroeder with Denning-Sacco Modification Alice Alice || Bob || r 1 { Alice || Bob || r 1 || ks || { Alice || T || ks } k. B } k. A { Alice || T || ks } k. B { r 2 } k s { r 2 – 1 } k s Cathy Bob Bob 15

Otway-Rees Protocol n Corrects problem n n Does not use timestamps n n That is, Eve replaying the third message in the protocol Not vulnerable to the problems that Denning-Sacco modification has Uses integer n to associate all messages with a particular exchange 16

The Protocol Alice n || Alice || Bob || { r 1 || n || Alice || Bob } k. A || Cathy { r 2 || n || Alice || Bob } k. B Cathy Alice n || { r 1 || ks } k. A || { r 2 || ks } k. B n || { r 1 || ks } k. A Bob Bob 17

Argument: Alice talking to Bob n Fourth message n n n If n matches first message, Alice knows it is part of this protocol exchange Cathy generated ks because only she, Alice know k. A Enciphered part belongs to exchange as r 1 matches r 1 in encrypted part of first message 18

Argument: Bob talking to Alice n Third message n n n If n matches second message, Bob knows it is part of this protocol exchange Cathy generated ks because only she, Bob know k. B Enciphered part belongs to exchange as r 2 matches r 2 in encrypted part of second message 19

Replay Attack n Eve acquires old ks, message in third step n n n || { r 1 || ks } k. A || { r 2 || ks } k. B Eve forwards appropriate part to Alice n n Alice has no ongoing key exchange with Bob: n matches nothing, so is rejected Alice has ongoing key exchange with Bob: n does not match, so is again rejected n If replay is for the current key exchange, and Eve sent the relevant part before Bob did, Eve could simply listen to traffic; no replay involved 20

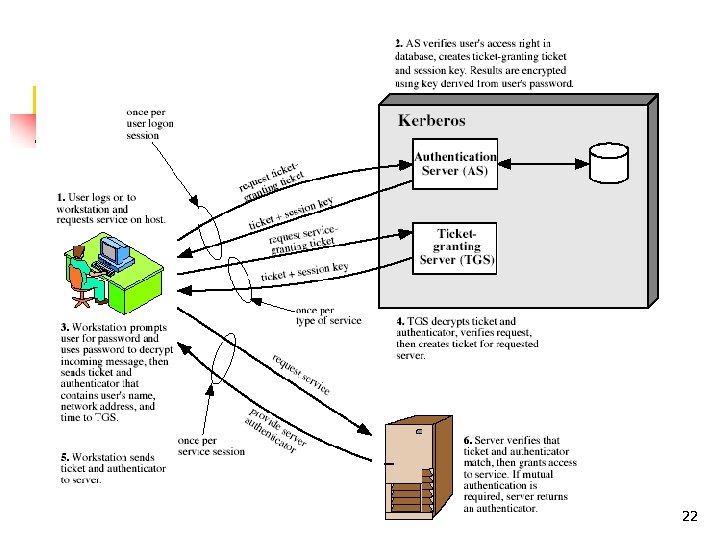
Kerberos n Authentication system n n n Ticket (credential) n n Issuer vouches for identity of requester of service Authenticator n n Based on Needham-Schroeder with Denning-Sacco modification Central server plays role of trusted third party (“Cathy”) Identifies sender Alice must 1. 2. Authenticate herself to the system Obtain ticket to use server S 21

22

Overview n User u authenticates to Kerberos server n n User u wants to use service s: n n Obtains ticket Tu, TGS for ticket granting service (TGS) User sends authenticator Au, ticket Tu, TGS to TGS asking for ticket for service TGS sends ticket Tu, s to user User sends Au, Tu, s to server as request to use s Details follow 23

Ticket n n Credential saying issuer has identified ticket requester Example ticket issued to user u for service s Tu, s = s || { u || u’s address || valid time || ku, s } ks where: n ku, s is session key for user and service n Valid time is interval for which the ticket is valid n u’s address may be IP address or something else n Note: more fields, but not relevant here 24

Authenticator n Credential containing identity of sender of ticket n n Used to confirm sender is entity to which ticket was issued Example: authenticator user u generates for service s Au, s = { u || generation time || kt } ku, s where: n kt is alternate session key n Generation time is when authenticator generated n Note: more fields, not relevant here 25

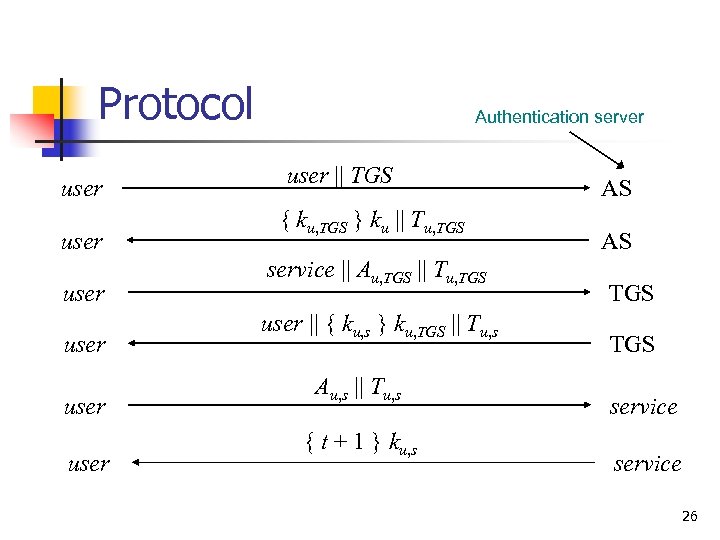Protocol user user Authentication server user || TGS { ku, TGS } ku || Tu, TGS service || Au, TGS || Tu, TGS user || { ku, s } ku, TGS || Tu, s Au, s || Tu, s { t + 1 } ku, s AS AS TGS service 26

Analysis n First two steps get user ticket to use TGS n n User u can obtain session key only if u knows key shared with Cathy Next four steps show u gets and uses ticket for service s n n Service s validates request by checking sender (using Au, s) is same as entity ticket issued to Step 6 optional; used when u requests confirmation 27

Problems n Relies on synchronized clocks n n If not synchronized and old tickets, authenticators not cached, replay is possible Tickets have some fixed fields n n Dictionary attacks possible Kerberos 4 session keys weak (had much less than 56 bits of randomness); researchers at Purdue found them from tickets in minutes 28

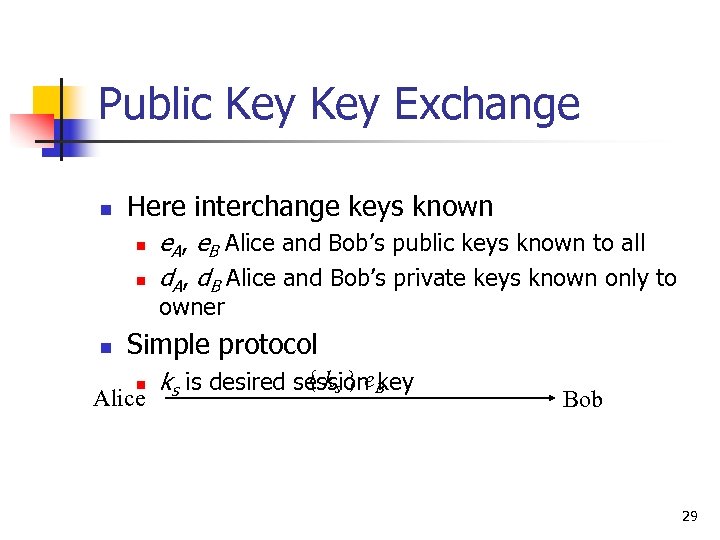Public Key Exchange n Here interchange keys known n n e. A, e. B Alice and Bob’s public keys known to all d. A, d. B Alice and Bob’s private keys known only to owner n Simple protocol n Alice { ks } e key ks is desired session B Bob 29

Problem and Solution n Vulnerable to forgery or replay n n Because e. B known to anyone, Bob has no assurance that Alice sent message Simple fix uses Alice’s private key { { ks } d. A } ks is desired session key e. B Alice n Bob 30

Notes n n Can include message enciphered with ks Assumes Bob has Alice’s public key, and vice versa n n If not, each must get it from public server If keys not bound to identity of owner, attacker Eve can launch a man-in-the-middle attack (next slide; Peter is public server providing public keys) 31

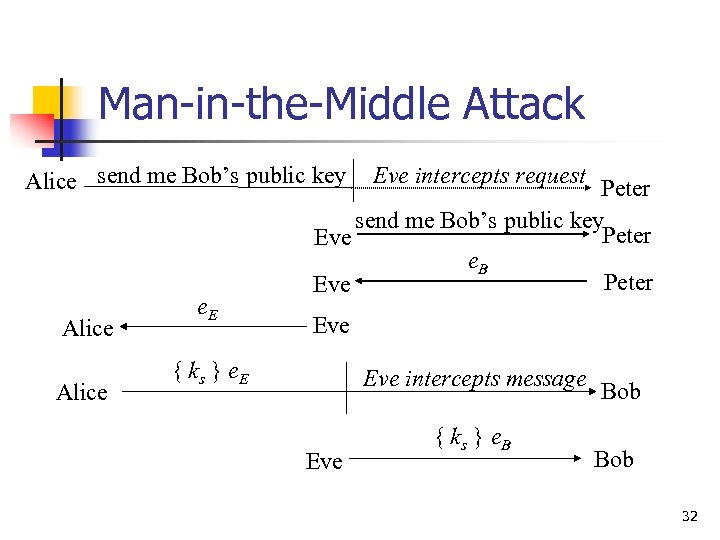Man-in-the-Middle Attack Alice send me Bob’s public key Alice e. E Eve intercepts request Peter send me Bob’s public key Peter Eve e. B Peter Eve { ks } e. E Eve intercepts message Eve { ks } e. B Bob 32

Key Generation n n Goal: generate difficult to guess keys Problem statement: given a set of K potential keys, choose one randomly n n Equivalent to selecting a random number between 0 and K– 1 inclusive Why is this hard: generating random numbers n Actually, numbers are usually pseudo-random, that is, generated by an algorithm 33

What is “Random”? n Sequence of cryptographically random numbers: a sequence of numbers n 1, n 2, … such that for any integer k > 0, an observer cannot predict nk even if all of n 1, …, nk– 1 are known n Best: physical source of randomness n n n Electromagnetic phenomena Characteristics of computing environment such as disk latency Ambient background noise 34

What is “Pseudorandom”? n Sequence of cryptographically pseudorandom numbers: sequence of numbers intended to simulate a sequence of cryptographically random numbers but generated by an algorithm n Very difficult to do this well n n n Linear congruential generators [nk = (ank– 1 + b) mod n] broken (a, b and n are relatively prime) Polynomial congruential generators [nk = (ajnk– 1 j + … + a 1 nk– 1 a 0) mod n] broken too Here, “broken” means next number in sequence can be determined 35

Best Pseudorandom Numbers n Strong mixing function: function of 2 or more inputs with each bit of output depending on some nonlinear function of all input bits n n Examples: DES, MD 5, SHA-1 Use on UNIX-based systems: (date; ps gaux) | md 5 where “ps gaux” lists all information about all processes on system 36

Cryptographic Key Infrastructure n n Goal: bind identity to key Classical Crypto: n n Not possible as all keys are shared Public key Crypto: n n Bind identity to public key Crucial as people will use key to communicate with principal whose identity is bound to key Erroneous binding means no secrecy between principals Assume principal identified by an acceptable name 37

Certificates n Create token (message) containing n n Identity of principal (here, Alice) Corresponding public key Timestamp (when issued) Other information (perhaps identity of signer) signed by trusted authority (here, Cathy) CA = { e. A || Alice || T } d. C CA is A’s certificate 38

Use n Bob gets Alice’s certificate n If he knows Cathy’s public key, he can decipher the certificate n n When was certificate issued? Is the principal Alice? Now Bob has Alice’s public key Problem: Bob needs Cathy’s public key to validate certificate n n Problem pushed “up” a level Two approaches: Merkle’s tree, signature chains 39

Merkle’s Tree Scheme n Keep certificates in a file n n n Changing any certificate changes the file Use crypto hash functions to detect this (data integrity) Define hashes recursively n h is hash function n Yi is certificate I (identity, Public key) n h(1, 4) h(1, 2) h(3, 4) h(1, 1) h(2, 2) h(3, 3) h(4, 4) Y 1 Y 2 Y 3 Y 4 Hash of file (h(1, 4) in example) known to all 40

Details n n f: D D D maps bit strings to bit strings h: N N D maps integers to bit strings n n if i ≥ j, h(i, j) = f(Yi, Yj) if i < j, h(i, j) = f(h(i, (i+j)/2 ), h( (i+j)/2 +1, j)) 41

Validation n h(1, 4) h(1, 2) h(3, 4) h(1, 1) h(2, 2) h(3, 3) h(4, 4) To validate Y 1: n Compute h(1, 1) n Obtain h(2, 2) n Compute h(1, 2) n Obtain h(3, 4) n Compute h(1, 4) n Y 1 Y 2 Y 3 Y 4 n Compare to known h(1, 4) Need to know hashes of children of nodes on path that are not computed 42

Problem n File must be available for validation n Otherwise, can’t recompute hash at root of tree Intermediate hashes would do Not practical in most circumstances n n Too many certificates and users Users and certificates distributed over widely separated systems 43

Certificate Signature Chains n Create certificate n n n Validate n n Generate hash of certificate Encipher hash with issuer’s private key Obtain issuer’s public key Decipher enciphered hash Recompute hash from certificate and compare Problem: n Validating the certificate of the issuer and getting issuer’s public key 44

X. 509 Chains n Key certificate fields in X. 509 v 3: n n n n Version Serial number (unique) Signature algorithm identifier Issuer’s name; uniquely identifies issuer Interval of validity Subject’s name; uniquely identifies subject Subject’s public key Signature: n Identifies algorithm used to sign the certificate n Signature (enciphered hash) 45

X. 509 Certificate Validation n Obtain issuer’s public key n n Decipher signature n n Gives hash of certificate Recompute hash from certificate and compare n n The one for the particular signature algorithm If they differ, there’s a problem Check interval of validity n This confirms that certificate is current 46

Issuers n Certification Authority (CA): entity that issues certificates n n n Multiple issuers pose validation problem Alice’s CA is Cathy; Bob’s CA is Dan; how can Alice validate Bob’s certificate? Have Cathy and Don cross-certify n Each issues certificate for the other 47

Validation and Cross-Certifying n Certificates: n Cathy<> n n n represents the certificate that C has generated for A Dan< Cathy<> Dan<> Alice validates Bob’s certificate n n n Alice obtains Cathy<> Alice uses (known) public key of Cathy to validate Cathy<> Alice uses Cathy<> to validate Dan<> n n Cathy<> Dan<> is a signature chain How about Bob validating Alice? 48

PGP Chains n Pretty Good Privacy: n n n Open. PGP certificates structured into packets n n n Widely used to provide privacy for electronic mail Sign files digitally One public key packet Zero or more signature packets Public key packet: n n n Version (3 or 4; 3 compatible with all versions of PGP, 4 not compatible with older versions of PGP) Creation time Validity period (not present in version 3) Public key algorithm, associated parameters Public key 49

Open. PGP Signature Packet n Version 3 signature packet n n n n n Version (3) Signature type (level of trust) Creation time (when next fields hashed) Signer’s key identifier (identifies key to encipher hash) Public key algorithm (used to encipher hash) Hash algorithm Part of signed hash (used for quick check) Signature (enciphered hash using signer’s private key) Version 4 packet more complex 50

Signing n n Single certificate may have multiple signatures Notion of “trust” embedded in each signature n n n Range from “untrusted” to “ultimate trust” Signer defines meaning of trust level (no standards!) All version 4 keys signed by subject n Called “self-signing” 51

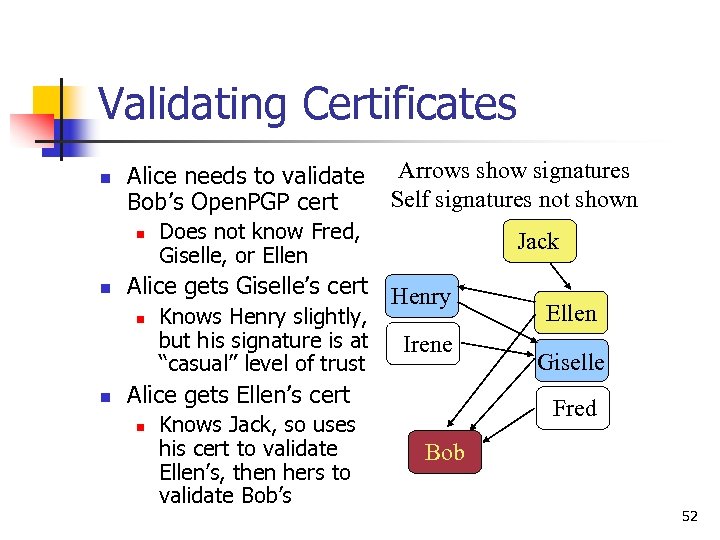Validating Certificates n Alice needs to validate Bob’s Open. PGP cert n n Does not know Fred, Giselle, or Ellen Jack Alice gets Giselle’s cert Henry n n Arrows show signatures Self signatures not shown Knows Henry slightly, but his signature is at “casual” level of trust Irene Alice gets Ellen’s cert n Knows Jack, so uses his cert to validate Ellen’s, then hers to validate Bob’s Ellen Giselle Fred Bob 52

Stream and Block Cipher n Block cipher (Ek is encryption) n n m = b 1 b 2…. , where bi is of a fixed length Ek(m) = Ek(b 1)Ek(b 2)… DES is a block cipher (64 bit blocks) Stream cipher (Ek is encryption) n n m = b 1 b 2…. , where bi is of a fixed length k = k 1 k 2…. Ek(m) = Ek 1(b 1)Ek 2(b 2)… Vinegere cipher, one-time pad 53

Digital Signature n n Construct that authenticates origin, contents of message in a manner provable to a disinterested third party (“judge”) Sender cannot deny having sent message (service is “nonrepudiation”) n Limited to technical proofs n n Inability to deny one’s cryptographic key was used to sign One could claim the cryptographic key was stolen or compromised n Legal proofs, etc. , probably required; 54

Common Error n Classical: Alice, Bob share key k n n Alice sends m || { m }k to Bob Does this satisfy the requirement for message authentication? How? Does this satisfy the requirement for a digital signature? This is not a digital signature n Why? Third party cannot determine whether Alice or Bob generated message 55

n Require trusted third party n n Alice, Bob each share keys with trusted party Cathy The judge must trust the trusted party Cathy Classical Digital Signatures To resolve dispute, judge gets { m }k. Alice, { m }k. Bob, { m }k. Alice and has Cathy decipher them; if messages matched, Alice contract was signed, else one is a forgery Bob { m }k. Alice Bob Cathy { m }k. Bob Cathy Bob n 56

Public Key Digital Signatures (RSA) n n Alice’s keys are d. Alice, e. Alice sends Bob m || { m }d. Alice n In case of dispute, judge computes { { m }d. Alice }e. Alice n and if it is m, Alice signed message n She’s the only one who knows d. Alice! 57

RSA Digital Signatures n Use private key to encipher message n n Protocol for use is critical Key points: n Never sign random documents, and when signing, always sign hash and never document n n Mathematical properties can be turned against signer Sign message first, then encipher n Changing public keys causes forgery 58

Attack #1 n n Example: Alice, Bob communicating n n. A = 95, e. A = 59, d. A = 11 n n. B = 77, e. B = 53, d. B = 17 26 contracts, numbered 00 to 25 n Alice has Bob sign 05 and 17: n n n c = md. B mod n. B = 0517 mod 77 = 3 c = md. B mod n. B = 1717 mod 77 = 19 Alice computes 05 17 mod 77 = 08; corresponding signature is 03 19 mod 77 = 57; claims Bob signed 08 Note: [(a mod n) × (b mod n)] mod n = (a × b) mod n Judge computes ce. B mod n. B = 5753 mod 77 = 08 n Signature validated; Bob is toast! 59

Attack #2: Bob’s Revenge n n n Bob, Alice agree to sign contract 06 Alice enciphers, then signs: e 53 mod 77)11 n Enciper: c = m B mod n. B = (06 d 53 mod 77)11 mod 95 = 63 n Sign: c A mod n. A = (06 Bob now changes his public key n Bob wants to claim that Alice singed N (13) Computes r such that 13 r mod 77 = 6; say, r = 59 n Computes r. e. B mod (n. B) = 59 53 mod 60 = 7 n Replace public key e. B with 7, private key d. B = 43 Bob claims contract was 13. Judge computes: 59 mod 95)43 mod 77 = 13 n (63 n Verified; now Alice is toast n n n Solution: sign first and then enciher!! 60

El Gamal Digital Signature n n n Relies on discrete log problem Choose p prime, g, d < p; Compute y = gd mod p Public key: (y, g, p); private key: d To sign contract m: n n n Choose k relatively prime to p– 1, and not yet used Compute a = gk mod p Find b such that m = (da + kb) mod p– 1 Signature is (a, b) To validate, check that n yaab mod p = gm mod p 61

Example n Alice chooses p = 29, g = 3, d = 6 y = 36 mod 29 = 4 n Alice wants to send Bob signed contract 23 n n n Chooses k = 5 (relatively prime to 28) This gives a = gk mod p = 35 mod 29 = 11 Then solving 23 = (6 11 + 5 b) mod 28 gives b = 25 Alice sends message 23 and signature (11, 25) Bob verifies signature: gm mod p = 323 mod 29 = 8 and yaab mod p = 4111125 mod 29 = 8 n They match, so Alice signed 62

Attack n Eve learns k, corresponding message m, and signature (a, b) n n Extended Euclidean Algorithm gives d, the private key Example from above: Eve learned Alice signed last message with k = 5 m = (da + kb) mod p– 1 = 23 =(11 d + 5 25) mod 28 So Alice’s private key is d = 6 63