IS 2150 TEL 2810 Introduction to Security

IS 2150 / TEL 2810 Introduction to Security September 14, 2006 Lecture 3 1

What is a secure system? n A simple definition n n A secure system doesn’t allow violations of a security policy Alternative view: based on distribution of rights to the subjects n Leakage of rights: (unsafe with respect to right r) n n Assume that A representing a secure state does not contain a right r in any element of A. A right r is said to be leaked, if a sequence of operations/commands adds r to an element of A, which did not contain r 2

What is a secure system? n Safety of a system with initial protection state Xo n Safe with respect to r: System is safe with respect to r if r can never be leaked n Else it is called unsafe with respect to right r. 3

Safety Problem: formally n Given n n initial state X 0 = (S 0, O 0, A 0) Set of primitive commands c r is not in A 0[s, o] Can we reach a state Xn where n s, o such that An[s, o] includes a right r not in A 0[s, o]? - If so, the system is not safe But is “safe” secure? 4

Decidability Results (Harrison, Ruzzo, Ullman) n Theorem: n Given a system where each command consists of a single primitive command (mono-operational), there exists an algorithm that will determine if a protection system with initial state X 0 is safe with respect to right r. 5

Decidability Results (Harrison, Ruzzo, Ullman) n Proof: determine minimum commands k to leak n n Delete/destroy: Can’t leak (or be detected) Create/enter: new subjects/objects “equal”, so treat all new subjects as one n n No test for absence Tests on A[s 1, o 1] and A[s 2, o 2] have same result as the same tests on A[s 1, o 1] and A[s 1, o 2] = A[s 1, o 2] A[s 2, o 2] If n rights leak possible, must be able to leak k= n(|S 0|+1)(|O 0|+1)+1 commands Enumerate all possible states to decide 6

Decidability Results (Harrison, Ruzzo, Ullman) n n It is undecidable if a given state of a given protection system is safe for a given generic right For proof – need to know Turing machines and halting problem 7

What is the implication? n Safety decidable for some models n n Are they practical? Safety only works if maximum rights known in advance n n Policy must specify all rights someone could get, not just what they have Where might this make sense? 8

Back to HRU: Fundamental questions n How can we determine that a system is secure? n n Need to define what we mean by a system being “secure” Is there a generic algorithm that allows us to determine whether a computer system is secure? 9

Turing Machine & halting problem n The halting problem: n Given a description of an algorithm and a description of its initial arguments, determine whether the algorithm, when executed with these arguments, ever halts (the alternative is that it runs forever without halting). 10

Turing Machine & halting problem n Reduce TM to Safety problem n If Safety problem is decidable then it implies that TM halts (for all inputs) – showing that the halting problem is decidable (contradiction) 11

Turing Machine n TM is an abstract model of computer n n Alan Turing in 1936 TM consists of n n A tape divided into cells; infinite in one direction A set of tape symbols M n n M contains a special blank symbol b A set of states K A head that can read and write symbols An action table that tells the machine n n n What symbol to write How to move the head (‘L’ for left and ‘R’ for right) What is the next state 12

Turing Machine n n The action table describes the transition function Transition function d(k, m) = (k , m , L): n n n in state k, symbol m on tape location is replaced by symbol m , head moves to left one square, and TM enters state k Halting state is qf n TM halts when it enters this state 13

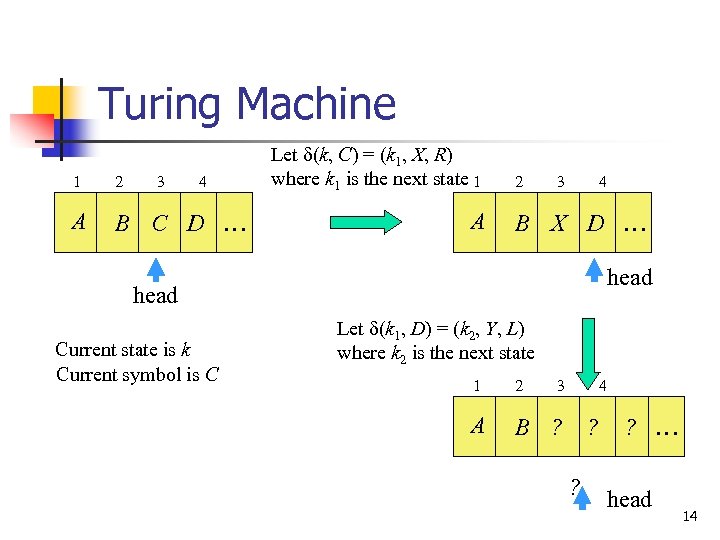Turing Machine 1 2 3 4 A B C D … Let d(k, C) = (k 1, X, R) where k 1 is the next state 1 A 2 3 4 B X D … head Current state is k Current symbol is C Let d(k 1, D) = (k 2, Y, L) where k 2 is the next state 1 2 3 A 4 B ? ? … head 14

General Safety Problem n n Theorem: It is undecidable if a given state of a given protection system is safe for a given generic right Proof: Reduce TM to safety problem n n n Symbols, States rights Tape cell subject Cell si has A rights on itself Cell sk has end rights on itself State p, head at si has p rights on itself Distinguished Right own: n si owns si+1 for 1 ≤ i < k 15

Command Mapping (Left move) d(k, C) = (k 1, X, L) If head is not in leftmost command ck, C(si, si-1) if own in a[si-1, si] and k in a[si, si] and C in a[si, si] then delete k from A[si, si]; delete C from A[si, si]; enter X into A[si, si]; enter k 1 into A[si-1, si-1]; End 16

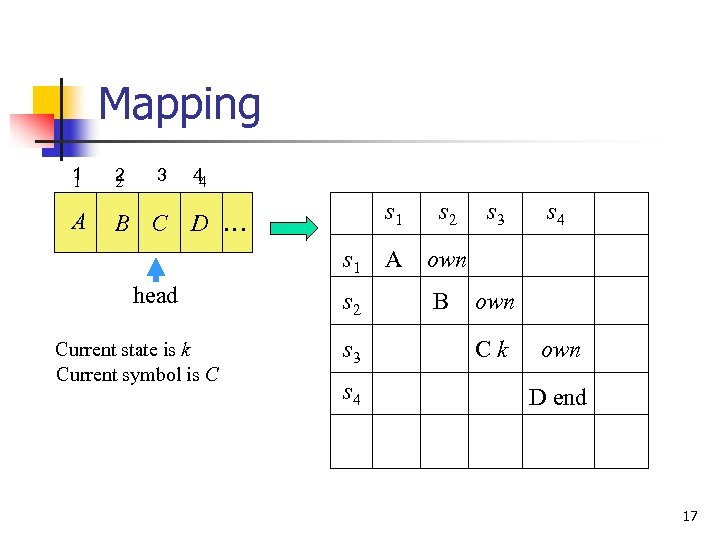Mapping 1 1 2 2 A B C 3 44 s 1 D … s 1 head Current state is k Current symbol is C s 2 s 3 s 4 s 2 A own B s 3 s 4 own Ck own D end 17

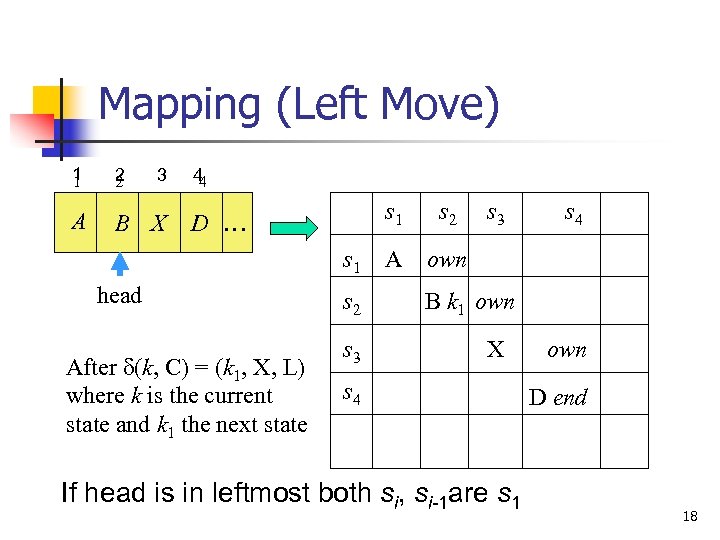Mapping (Left Move) 1 1 2 2 A B X 3 44 s 1 D … s 1 head After d(k, C) = (k 1, X, L) where k is the current state and k 1 the next state s 2 s 3 s 2 A s 3 s 4 own B k 1 own X s 4 If head is in leftmost both si, si-1 are s 1 own D end 18

Command Mapping (Right move) d(k, C) = (k 1, X, R) command ck, C(si, si+1) if own in a[si, si+1] and k in a[si, si] and C in a[si, si] then delete k from A[si, si]; delete C from A[si, si]; enter X into A[si, si]; enter k 1 into A[si+1, si+1]; end 19

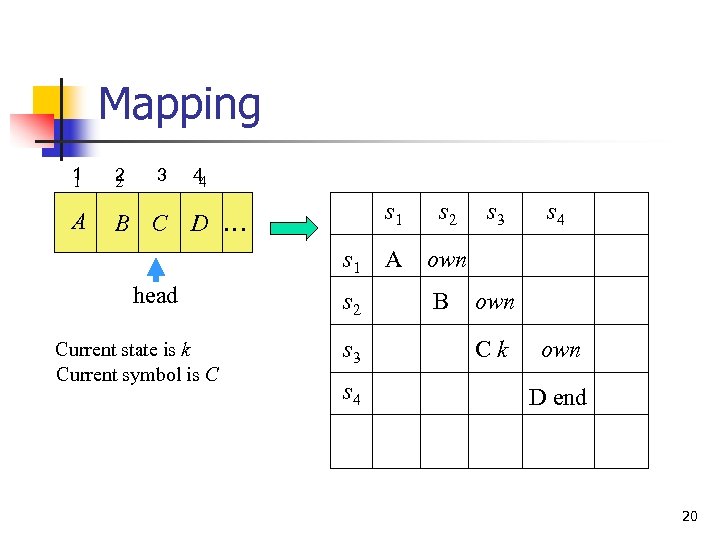Mapping 1 1 2 2 A B C 3 44 s 1 D … s 1 head Current state is k Current symbol is C s 2 s 3 s 4 s 2 A own B s 3 s 4 own Ck own D end 20

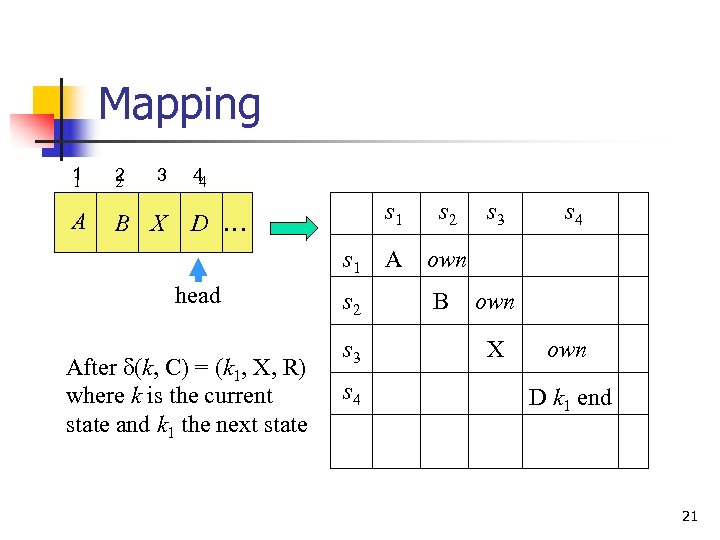Mapping 1 1 2 2 A B X 3 44 s 1 D … s 1 head After d(k, C) = (k 1, X, R) where k is the current state and k 1 the next state s 2 s 3 s 4 s 2 A own B s 3 s 4 own X own D k 1 end 21

Command Mapping (Rightmost move) d(k 1, D) = (k 2, Y, R) at end becomes command crightmostk, C(si, si+1) if end in a[si, si] and k 1 in a[si, si] and D in a[si, si] then delete end from a[si, si]; create subject si+1; enter own into a[si, si+1]; enter end into a[si+1, si+1]; delete k 1 from a[si, si]; delete D from a[si, si]; enter Y into a[si, si]; enter k 2 into A[si, si]; end 22

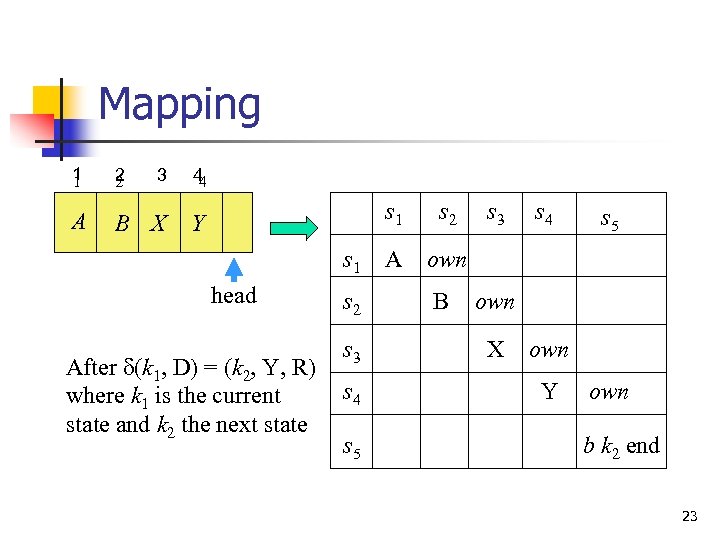Mapping 1 1 2 2 3 44 A B X Y s 1 head After d(k 1, D) = (k 2, Y, R) where k 1 is the current state and k 2 the next state s 2 s 3 s 4 s 5 s 2 A own B s 3 s 4 s 5 own X own Y own b k 2 end 23

Rest of Proof n n n Protection system exactly simulates a TM n Exactly 1 end right in ACM n Only 1 right corresponds to a state n Thus, at most 1 applicable command in each configuration of the TM If TM enters state qf, then right has leaked If safety question decidable, then represent TM as above and determine if qf leaks n n Leaks halting state in the matrix Halting state reached Conclusion: safety question undecidable 24

Security Policy n n Defines what it means for a system to be secure Formally: Partitions a system into n n n Set of secure (authorized) states Set of non-secure (unauthorized) states Secure system is one that n n Starts in authorized state Cannot enter unauthorized state 25

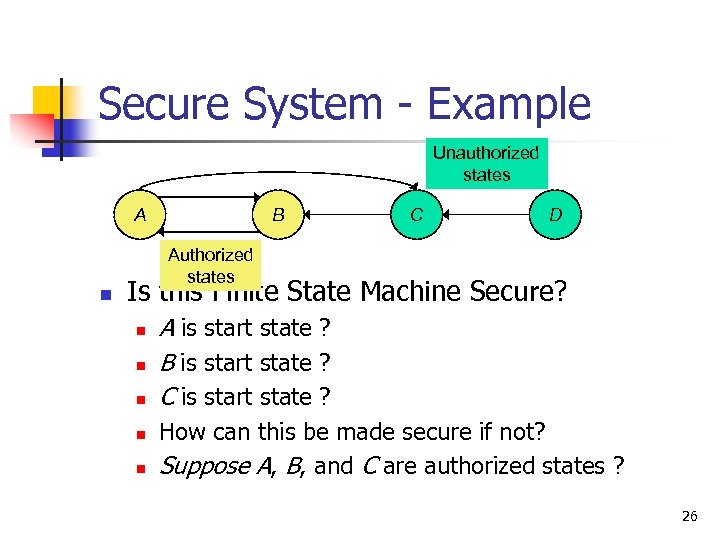Secure System - Example Unauthorized states A n B C D Authorized states Is this Finite State Machine Secure? n n n A is start state ? B is start state ? C is start state ? How can this be made secure if not? Suppose A, B, and C are authorized states ? 26

Additional Definitions: n n Security breach: system enters an unauthorized state Let X be a set of entities, I be information. n n I has confidentiality with respect to X if no member of X can obtain information on I I has integrity with respect to X if all members of X trust I n n Trust I, its conveyance and protection (data integrity) I maybe origin information or an identity (authentication) I is a resource – its integrity implies it functions as it should (assurance) I has availability with respect to X if all members of X can access I n Time limits (quality of service 27

Confidentiality Policy n Also known as information flow n n Model often depends on trust n n n Transfer of rights Transfer of information without transfer of rights Temporal context Parts of system where information could flow Trusted entity must participate to enable flow Highly developed in Military/Government 28

Integrity Policy n Defines how information can be altered n n Examples: n n n Entities allowed to alter data Conditions under which data can be altered Limits to change of data Purchase over $1000 requires signature Check over $10, 000 must be approved by one person and cashed by another n Separation of duties : for preventing fraud Highly developed in commercial world 29

Transaction-oriented Integrity n Begin in consistent state n n “Consistent” defined by specification Perform series of actions (transaction) n n n Actions cannot be interrupted If actions complete, system in consistent state If actions do not complete, system reverts to beginning (consistent) state 30

Trust n n Theories and mechanisms rest on some trust assumptions Administrator installs patch 1. 2. 3. 4. Trusts patch came from vendor, not tampered with in transit Trusts vendor tested patch thoroughly Trusts vendor’s test environment corresponds to local environment Trusts patch is installed correctly 31

Trust in Formal Verification n Formal verification provides a formal mathematical proof that given input i, program P produces output o as specified Suppose a security-related program S formally verified to work with operating system O What are the assumptions? 32

Trust in Formal Methods Proof has no errors 1. n Bugs in automated theorem provers Preconditions hold in environment in which S is to be used S transformed into executable S’ whose actions follow source code 2. 3. n Compiler bugs, linker/loader/library problems Hardware executes S’ as intended 4. n Hardware bugs 33

Security Mechanism n n Policy describes what is allowed Mechanism n n Example Policy: Students should not copy homework n n Is an entity/procedure that enforces (part of) policy Mechanism: Disallow access to files owned by other users Does mechanism enforce policy? 34

Common Mechanisms: Access Control n Discretionary Access Control (DAC) n n n Mandatory Access Control (MAC) n n n Owner determines access rights Typically identity-based access control: Owner specifies other users who have access Rules specify granting of access Also called rule-based access control Originator Controlled Access Control (ORCON) n n n Originator controls access Originator need not be owner! Role Based Access Control (RBAC) n Identity governed by role user assumes 35