Ions in an electrostatic ion beam trap 4

Ions in an electrostatic ion beam trap 4 th LEIF meeting Belfast 2003 Oded Heber Weizmann Institute of Science Israel Chemistry: • Yinon Rudich • Irit Sagi Physics: • Daniel Zajfman • Henrik Pedersen (now at MPI) • Michael Rappaport • Sarah Goldberg • Adi Naaman • Daniel Strasser • Peter Witte (also MPI) • Nissan Altstein • Daniel Savin

TALK SUBJECTS • INTRODUCTION: ELETROSTATIC LINEAR TRAP AND LAB • DYNAMICS OF ION BUNCHES IN THE TRAP • LONG TIME SYNCRONIZATION MODE • DIFFUSION MODE

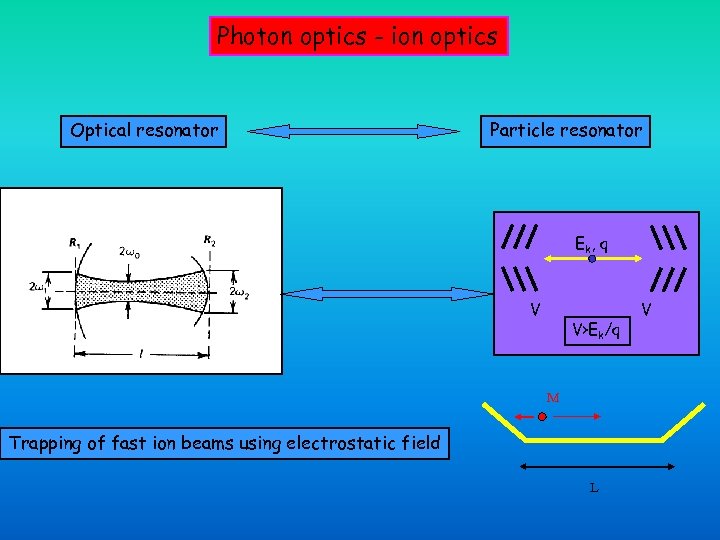
Photon optics - ion optics Optical resonator Particle resonator Ek , q V V>Ek/q M Trapping of fast ion beams using electrostatic field L V

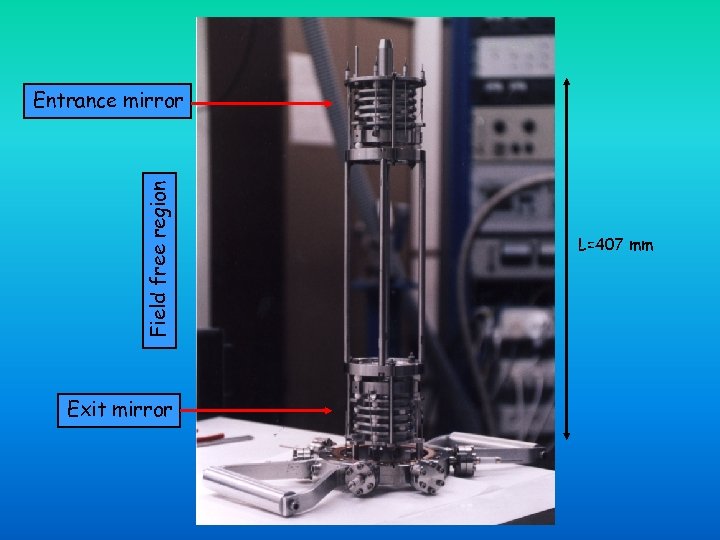
Field free region Entrance mirror Exit mirror L=407 mm

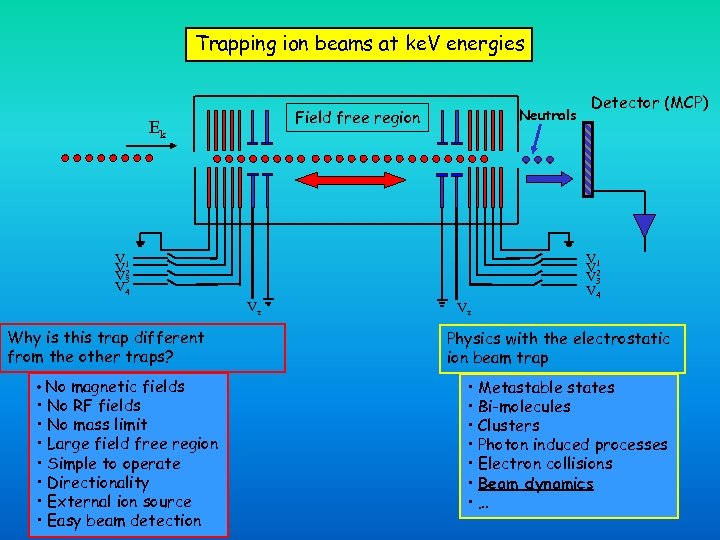
Trapping ion beams at ke. V energies Neutrals Field free region Ek V 1 V 2 V 3 V 4 Vz Why is this trap different from the other traps? • No magnetic fields • No RF fields • No mass limit • Large field free region • Simple to operate • Directionality • External ion source • Easy beam detection Vz Detector (MCP) V 1 V 2 V 3 V 4 Physics with the electrostatic ion beam trap • Metastable states • Bi-molecules • Clusters • Photon induced processes • Electron collisions • Beam dynamics • …

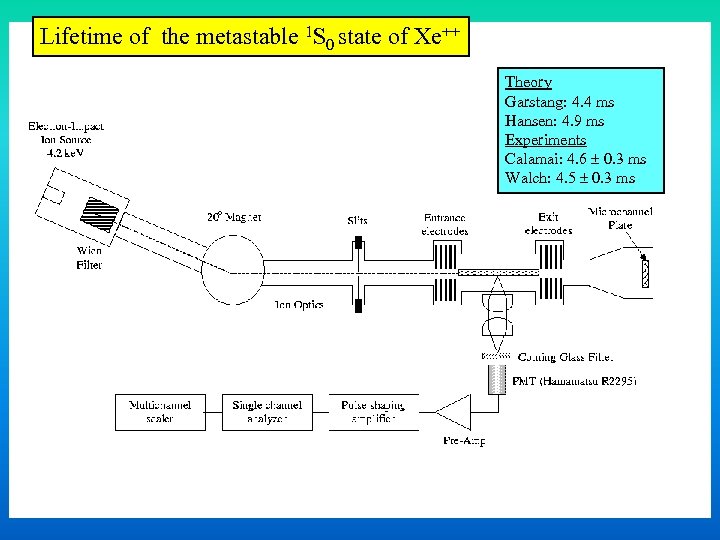
Lifetime of the metastable 1 S 0 state of Xe++ Theory Garstang: 4. 4 ms Hansen: 4. 9 ms Experiments Calamai: 4. 6 0. 3 ms Walch: 4. 5 0. 3 ms

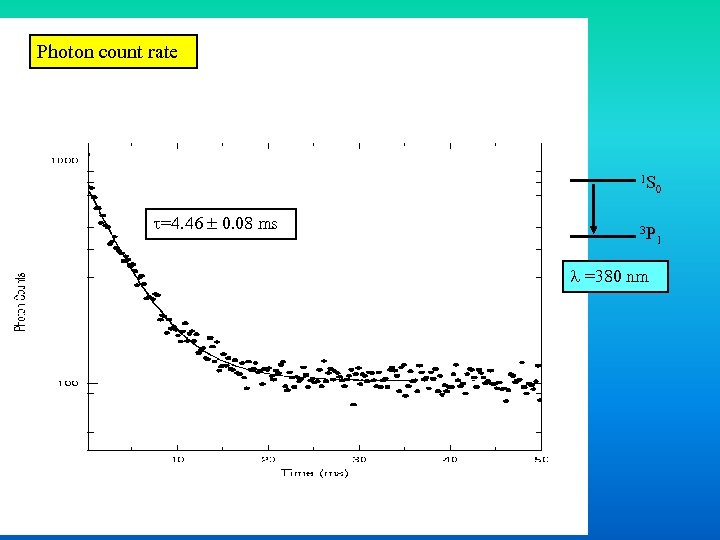
Photon count rate 1 S =4. 46 0. 08 ms 0 3 P =380 nm 1

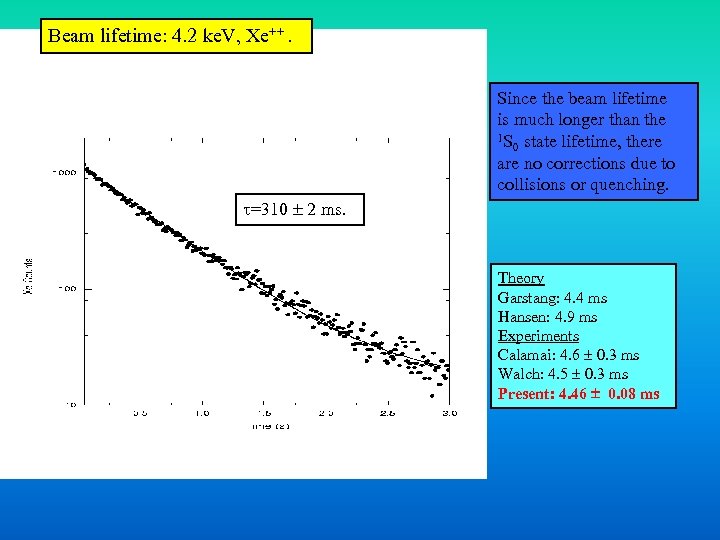
Beam lifetime: 4. 2 ke. V, Xe++. Since the beam lifetime is much longer than the 1 S state lifetime, there 0 are no corrections due to collisions or quenching. =310 2 ms. Theory Garstang: 4. 4 ms Hansen: 4. 9 ms Experiments Calamai: 4. 6 0. 3 ms Walch: 4. 5 0. 3 ms Present: 4. 46 0. 08 ms

Linear trap control room Laser room Bent trap Ion sources Source control

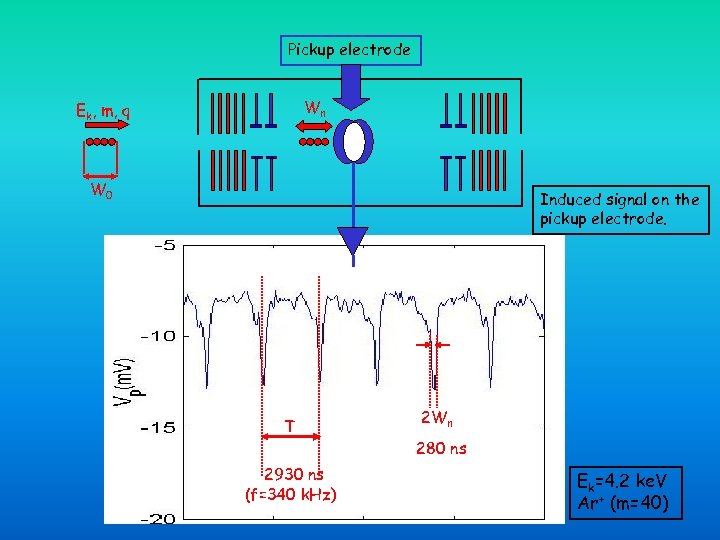
Pickup electrode Wn Ek, m, q W 0 Induced signal on the pickup electrode. T 2930 ns (f=340 k. Hz) 2 Wn 280 ns Ek=4. 2 ke. V Ar+ (m=40)

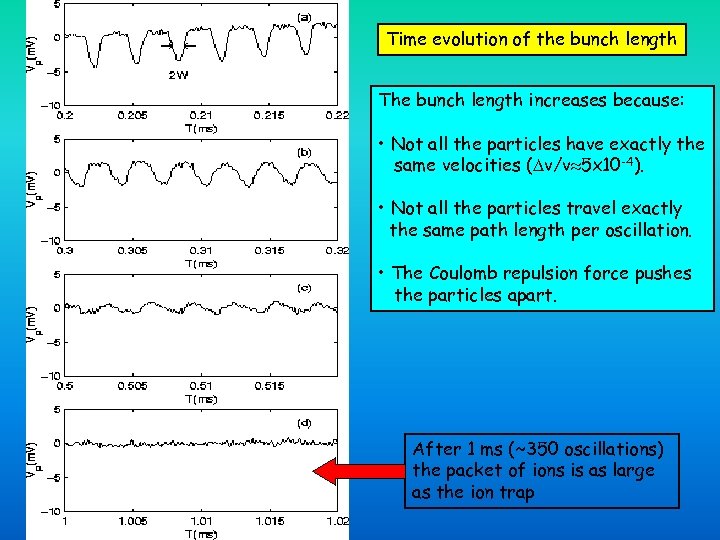
Time evolution of the bunch length The bunch length increases because: • Not all the particles have exactly the same velocities ( v/v 5 x 10 -4). • Not all the particles travel exactly the same path length per oscillation. • The Coulomb repulsion force pushes the particles apart. After 1 ms (~350 oscillations) the packet of ions is as large as the ion trap

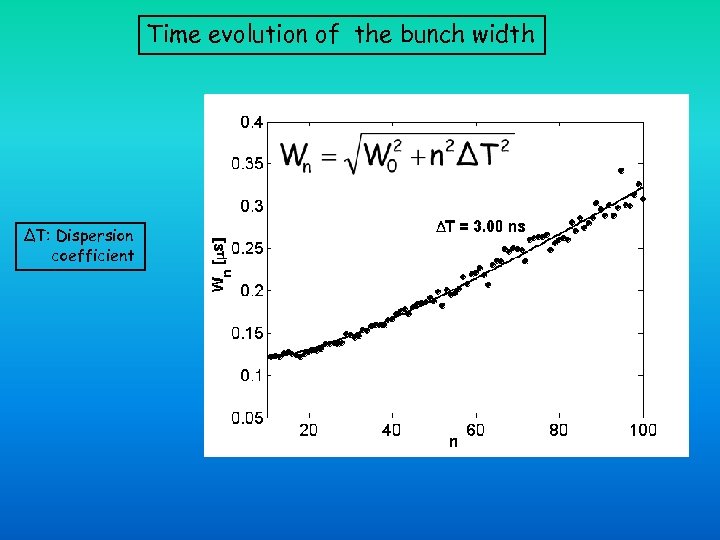
Time evolution of the bunch width ΔT: Dispersion coefficient

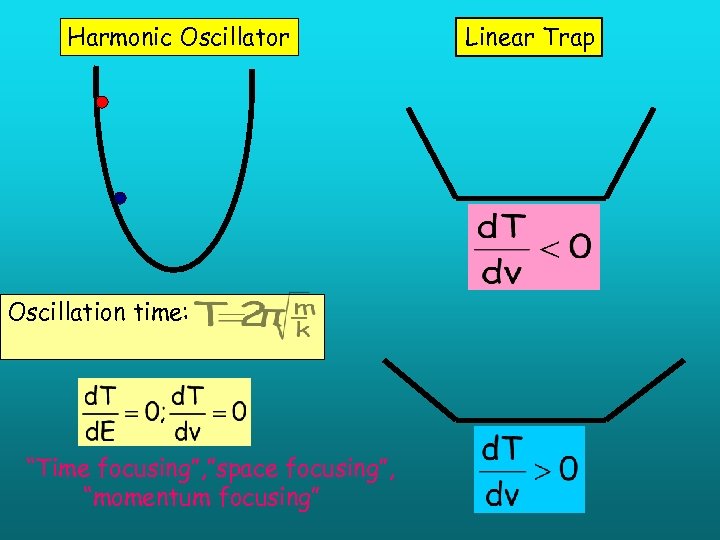
Harmonic Oscillator Oscillation time: “Time focusing”, ”space focusing”, “momentum focusing” Linear Trap

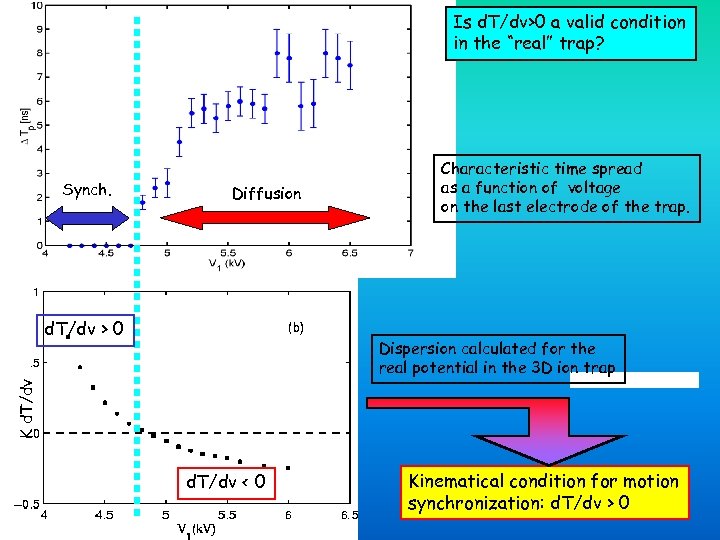
Is d. T/dv>0 a valid condition in the “real” trap? Synch. Diffusion d. T/dv > 0 Characteristic time spread as a function of voltage on the last electrode of the trap. K d. T/dv Dispersion calculated for the real potential in the 3 D ion trap d. T/dv < 0 Kinematical condition for motion synchronization: d. T/dv > 0

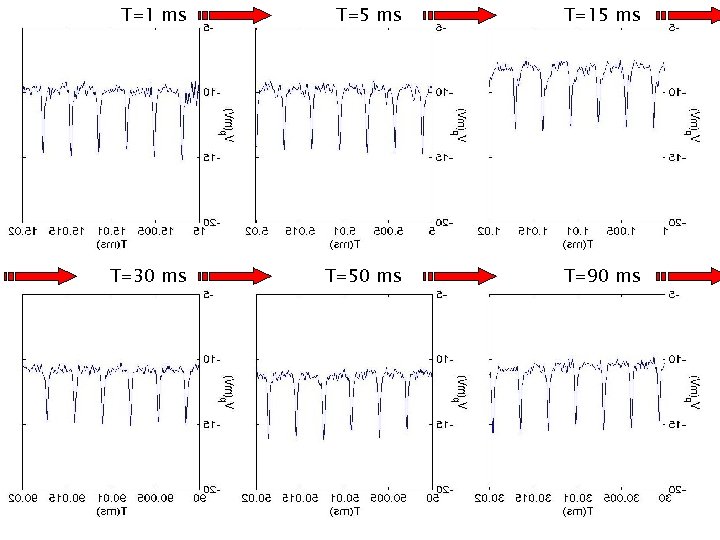
T=1 ms T=5 ms T=15 ms T=30 ms T=50 ms T=90 ms

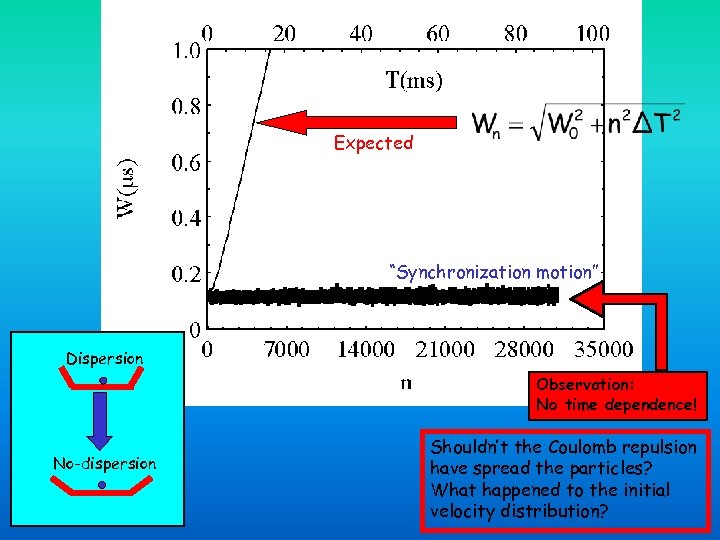
Expected “Synchronization motion” Dispersion Observation: No time dependence! No-dispersion Shouldn’t the Coulomb repulsion have spread the particles? What happened to the initial velocity distribution?

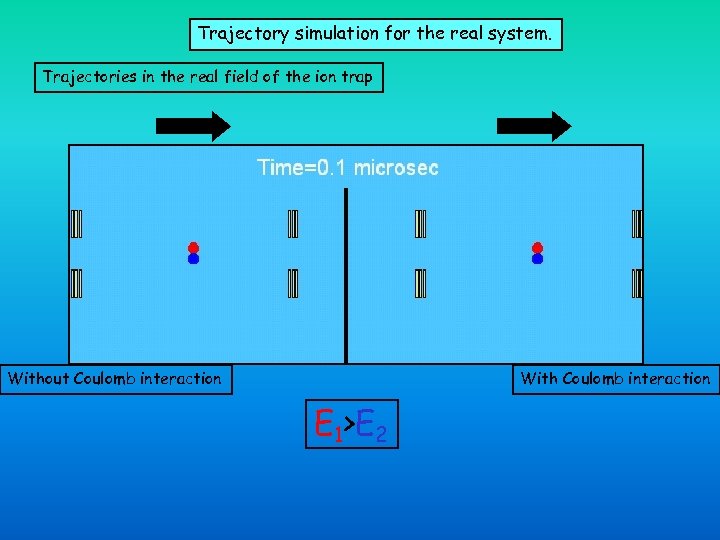
Trajectory simulation for the real system. Trajectories in the real field of the ion trap Without Coulomb interaction With Coulomb interaction E 1>E 2

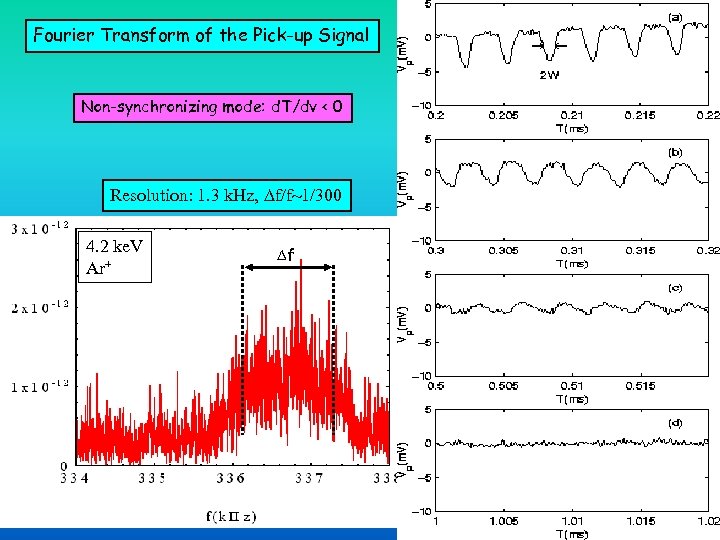
Fourier Transform of the Pick-up Signal Non-synchronizing mode: d. T/dv < 0 Resolution: 1. 3 k. Hz, f/f 1/300 4. 2 ke. V Ar+ f .

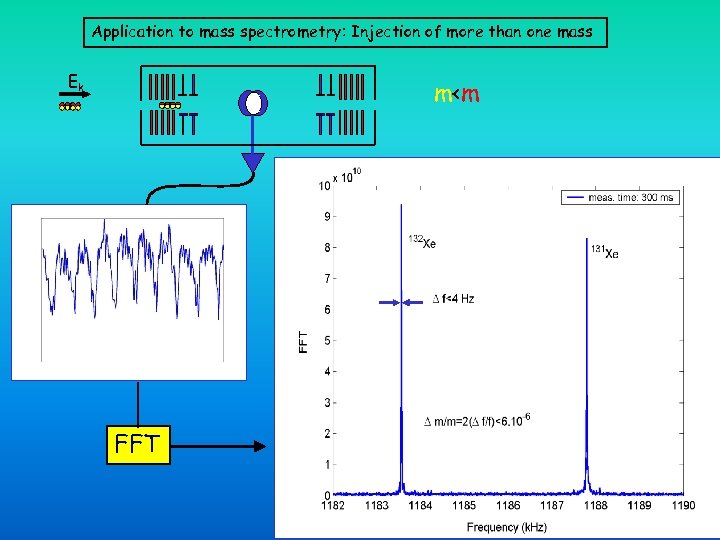
Application to mass spectrometry: Injection of more than one mass Ek m<m FFT

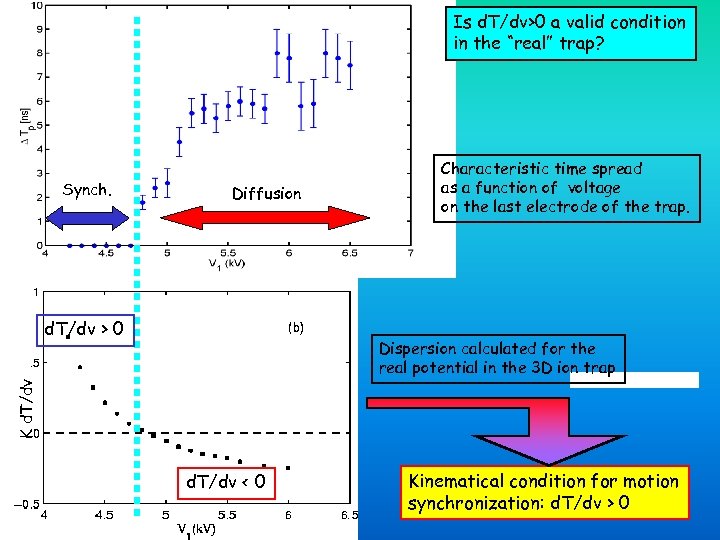
Is d. T/dv>0 a valid condition in the “real” trap? Synch. Diffusion d. T/dv > 0 Characteristic time spread as a function of voltage on the last electrode of the trap. K d. T/dv Dispersion calculated for the real potential in the 3 D ion trap d. T/dv < 0 Kinematical condition for motion synchronization: d. T/dv > 0

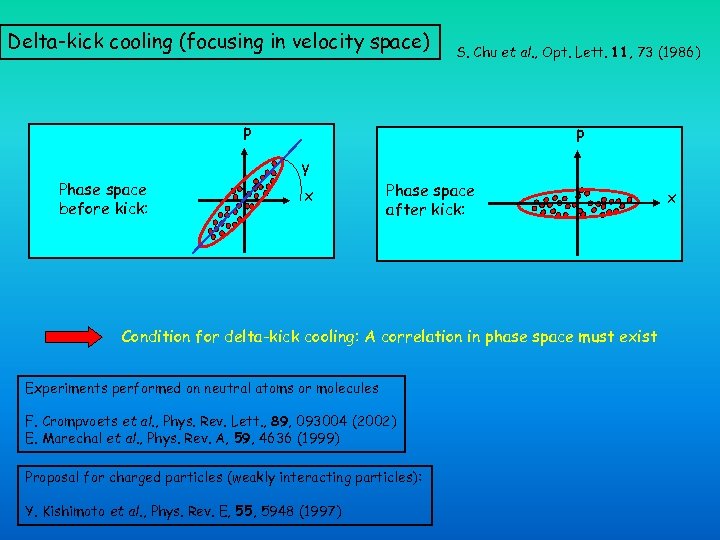
Delta-kick cooling (focusing in velocity space) S. Chu et al. , Opt. Lett. 11, 73 (1986) p Phase space before kick: p γ x Phase space after kick: Condition for delta-kick cooling: A correlation in phase space must exist Experiments performed on neutral atoms or molecules F. Crompvoets et al. , Phys. Rev. Lett. , 89, 093004 (2002) E. Marechal et al. , Phys. Rev. A, 59, 4636 (1999) Proposal for charged particles (weakly interacting particles): Y. Kishimoto et al. , Phys. Rev. E, 55, 5948 (1997) x

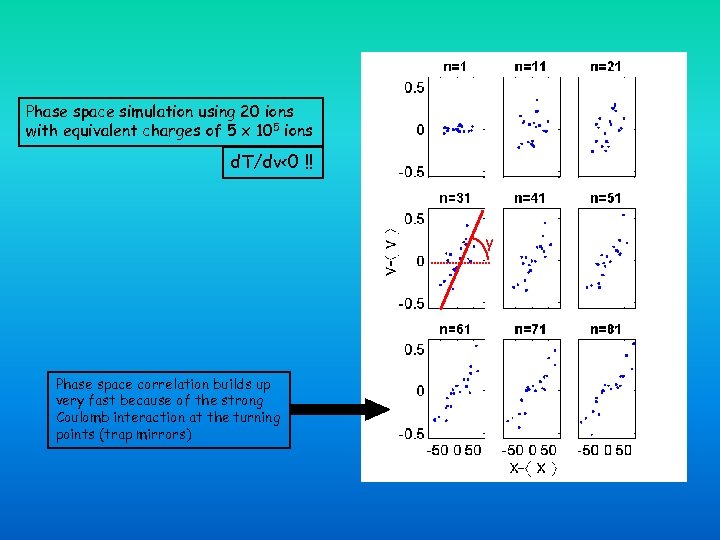
Phase space simulation using 20 ions with equivalent charges of 5 x 105 ions d. T/dv<0 !! γ Phase space correlation builds up very fast because of the strong Coulomb interaction at the turning points (trap mirrors)

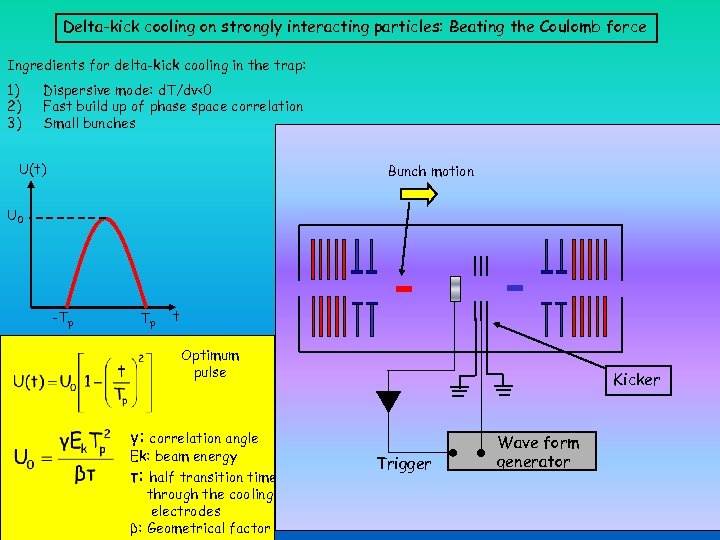
Delta-kick cooling on strongly interacting particles: Beating the Coulomb force Ingredients for delta-kick cooling in the trap: 1) 2) 3) Dispersive mode: d. T/dv<0 Fast build up of phase space correlation Small bunches U(t) Bunch motion U 0 -Tp Tp t Optimum pulse Kicker γ: correlation angle Ek: beam energy τ: half transition time through the cooling electrodes β: Geometrical factor Trigger Wave form generator

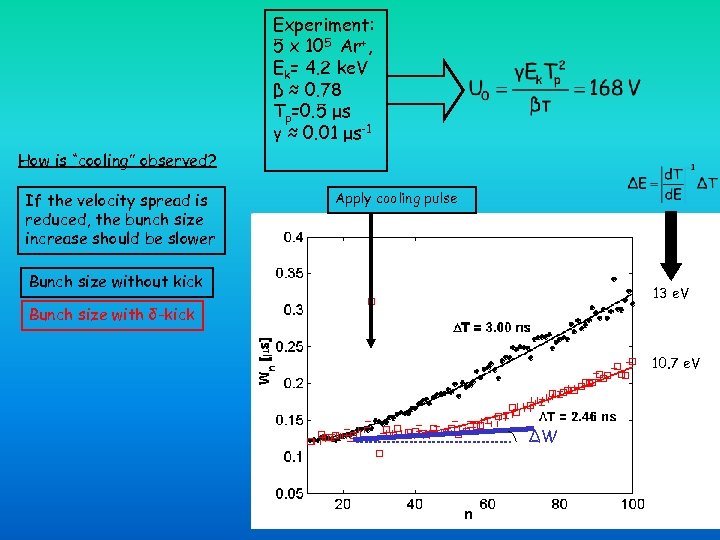
Experiment: 5 x 105 Ar+, Ek= 4. 2 ke. V β ≈ 0. 78 Tp=0. 5 μs γ ≈ 0. 01 μs-1 How is “cooling” observed? If the velocity spread is reduced, the bunch size increase should be slower Apply cooling pulse Bunch size without kick 13 e. V Bunch size with δ-kick 10. 7 e. V ΔW

Summery: Ion bunch motion in the electrostatic trap can be in a synchronization mode when d. T/dv>0 Application: high resolution mass spectrometry When d. T/dv<0 the bunch is in an enhanced diffusion mode Application: delta kick cooling Ion Motion Synchronization in an Ion-Trap Resonator, • Phys. Rev. Lett. , pp. 55001, 87 (2001). • Phys. Rev. A. , pp. 42703, 65 (2002). • Phys. Rev. A, pp. 42704, 65 (2002). • Phys. Rev. Lett. , pp. 283204, 89 (2002) Delta Kick Cooling • Submitted to Phys. Rev. A