Ionic Bonding Whereas the term covalent implies sharing

Ionic Bonding Whereas the term covalent implies sharing of electrons between atoms, the term ionic indicates that electrons are taken from one atom by another. The nature of ionic bonding is very different than that of covalent bonding and must be considered using different approaches. Some aspects to remember: 1. Electronegative atoms will generally gain enough electrons to fill their valence shell and more electropositive atoms will lose enough electrons to empty their valence shell. e. g. Na: [Ne]3 s 1 Na+: [Ne] Cl: [Ne]3 s 2 3 p 5 Cl-: [Ar] Ca: [Ar]4 s 2 Ca+2: [Ar] O: [He]2 s 2 2 p 4 O-2: [Ne] 2. Ions are considered to be spherical and their size is given by the ionic radii that have been defined for most elements (there is a table in the notes on Atomic Structure). The structures of the salts formed from ions is based on the close packing of spheres. 3. The cations and anions are held together by electrostatic attraction. mutuslab. cs. uwindsor. ca/. . . /Bonding-Notes 9. ppt

Ionic Bonding Because electrostatic attraction is not directional in the same way as is covalent bonding, there are many more possible structural types. However, in the solid state, all ionic structures are based on infinite lattices of cations and anions. There are some important classes that are common and that you should be able to identify, including: Na. Cl Cs. Cl Fluorite Zinc Blende Wurtzite And others…Fortunately, we can use the size of the ions to find out what kind of structure an ionic solid should adopt and we will use the structural arrangement to determine the energy that holds the solid together - the crystal lattice energy, U 0.

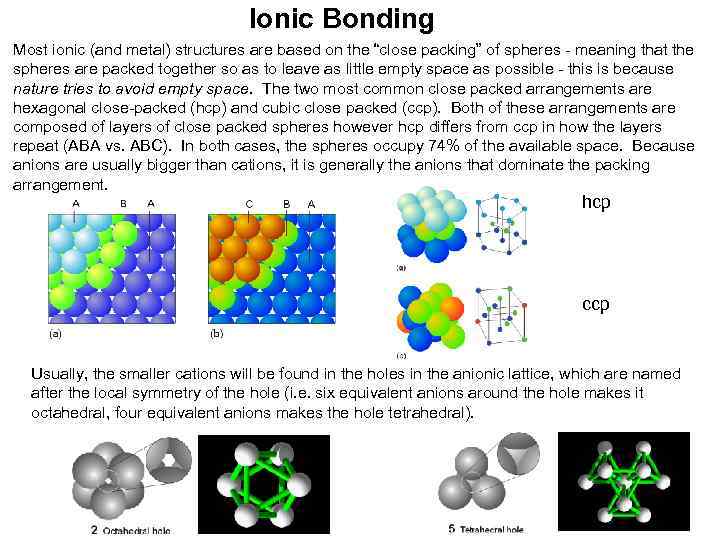
Ionic Bonding Most ionic (and metal) structures are based on the “close packing” of spheres - meaning that the spheres are packed together so as to leave as little empty space as possible - this is because nature tries to avoid empty space. The two most common close packed arrangements are hexagonal close-packed (hcp) and cubic close packed (ccp). Both of these arrangements are composed of layers of close packed spheres however hcp differs from ccp in how the layers repeat (ABA vs. ABC). In both cases, the spheres occupy 74% of the available space. Because anions are usually bigger than cations, it is generally the anions that dominate the packing arrangement. hcp ccp Usually, the smaller cations will be found in the holes in the anionic lattice, which are named after the local symmetry of the hole (i. e. six equivalent anions around the hole makes it octahedral, four equivalent anions makes the hole tetrahedral).

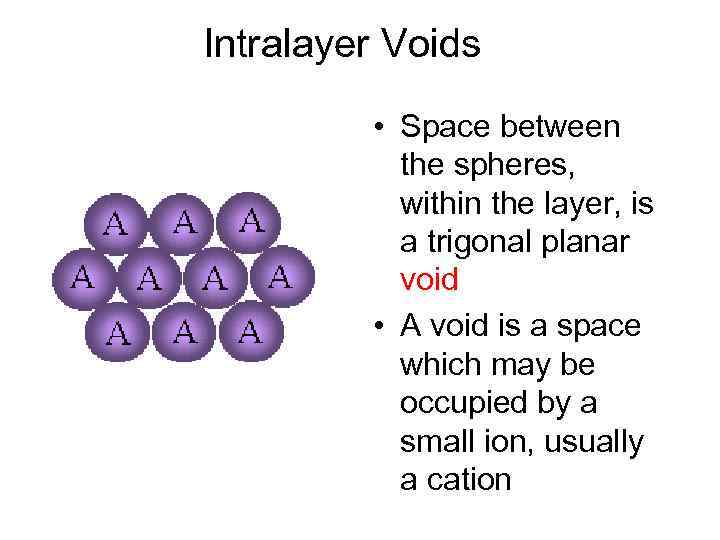
Intralayer Voids • Space between the spheres, within the layer, is a trigonal planar void • A void is a space which may be occupied by a small ion, usually a cation

Void: Sphere Ratio • Ratio of voids/spheres • Around each sphere there are six voids • Around each void there are three spheres • The ratio of voids/spheres is therefore 2: 1

Interlayer Voids • Both types of packing have empty places (voids) between layers • There are two types of voids • Each has a different CN

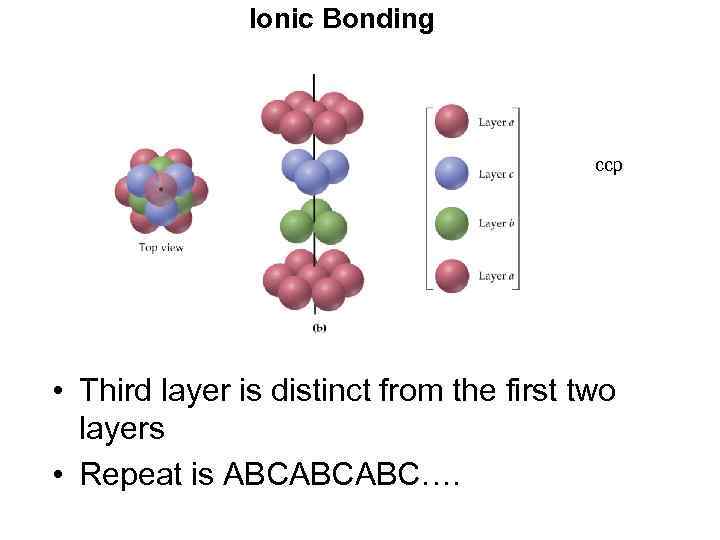
Ionic Bonding ccp • Third layer is distinct from the first two layers • Repeat is ABCABCABC….

Single Element Packing Square Lattice first layer Simple Cubic Lattice Packing used by e. g. Po. second layer (directly above first)

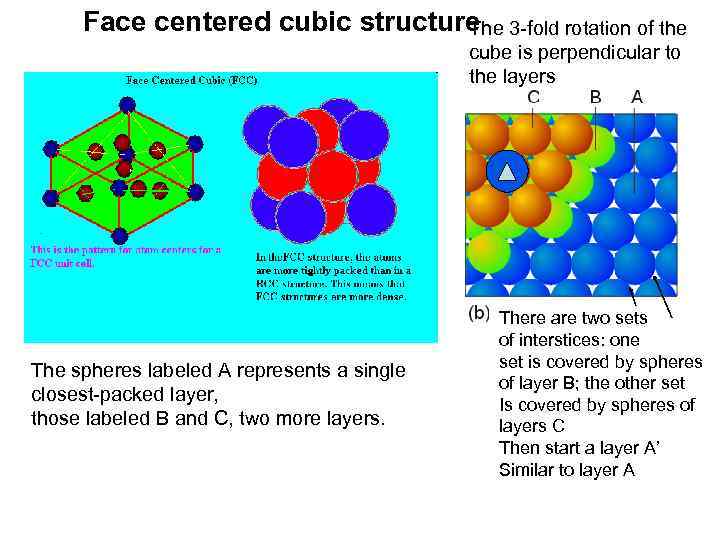
Face centered cubic structure The 3 -fold rotation of the cube is perpendicular to the layers The spheres labeled A represents a single closest-packed layer, those labeled B and C, two more layers. There are two sets of interstices: one set is covered by spheres of layer B; the other set Is covered by spheres of layers C Then start a layer A’ Similar to layer A

Face centered cubic structure Closest Packed Lattice Two types of indentations A. Directly over first layer. B. Over first layer indentation. first layer second layer (over any indentation) So, two different places to start third layer! A A B B

Face centered cubic structure Closest Packed Lattice Two types of indentations A. Directly over first layer. B. Over first layer indentation. first layer second layer (over any indentation) A A B B So, two different places to start third layer! IF directly over A, get ABAB packing, also known as hexagonal closest packed (hcp). Used by Mg, Ca, Co, Zn, etc.

Face centered cubic structure Closest Packed Lattice Two types of indentations A. Directly over first layer. B. Over first layer indentation. first layer second layer (over any indentation) So, two different places to start third layer! IF third layer directly over B, get ABCABC packing, also known as face centered cubic (fcc). Used by Al, Cu, Ni, Ag, Au etc.

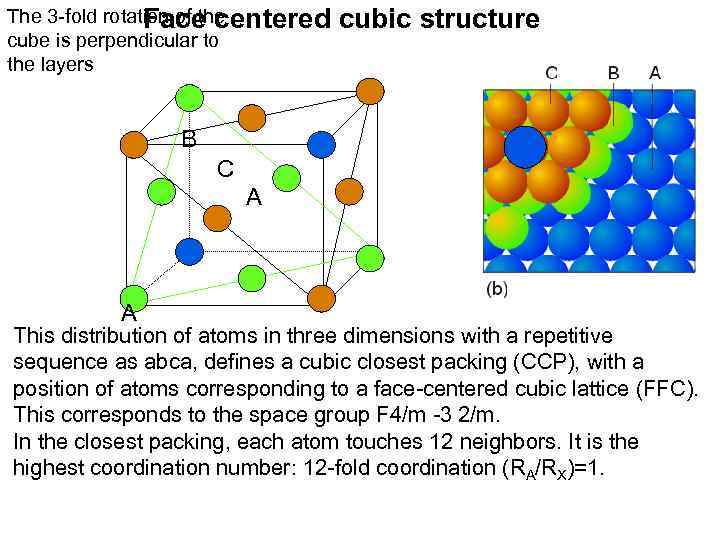
The 3 -fold rotation of the Face centered cube is perpendicular to the layers cubic structure B C A A This distribution of atoms in three dimensions with a repetitive sequence as abca, defines a cubic closest packing (CCP), with a position of atoms corresponding to a face-centered cubic lattice (FFC). This corresponds to the space group F 4/m -3 2/m. In the closest packing, each atom touches 12 neighbors. It is the highest coordination number: 12 -fold coordination (RA/RX)=1.

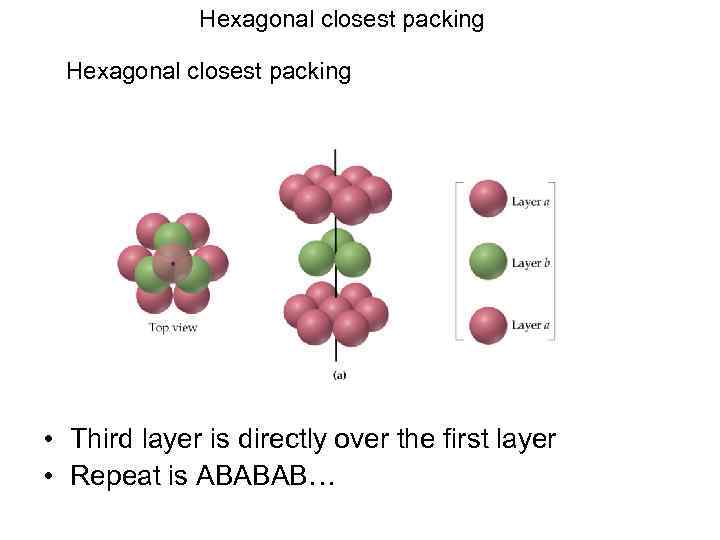
Hexagonal closest packing • Third layer is directly over the first layer • Repeat is ABABAB…

Hexagonal closest packing Similarly, it may be defined a Hexagonal Closest Packing (HCP), when layers show the following succession ABA. Identipoints define the hexagonal lattice underlying HCP. The resultant space group is P 63/m 2/c. The is also a high coordination number: 12 -fold coordination (RA/RX)=1.

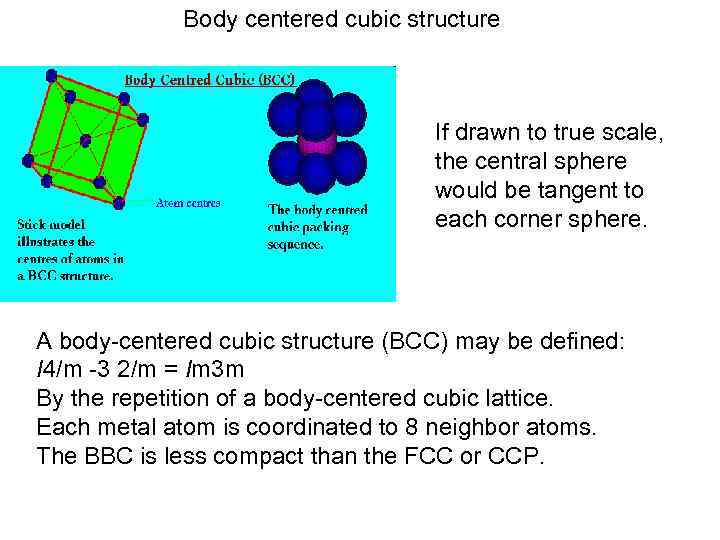
Body centered cubic structure If drawn to true scale, the central sphere would be tangent to each corner sphere. A body-centered cubic structure (BCC) may be defined: I 4/m -3 2/m = Im 3 m By the repetition of a body-centered cubic lattice. Each metal atom is coordinated to 8 neighbor atoms. The BBC is less compact than the FCC or CCP.

Body-centered cubic lattice Square Lattice BCC Lattice Packing used by e. g. Li, K, V, Fe, W, etc. first layer second layer (sitting in indentations) third layer (directly above first)

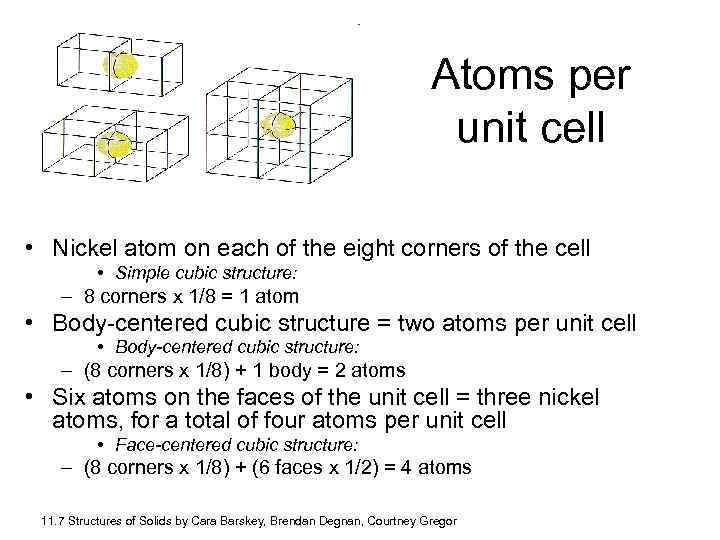
Atoms per unit cell • Nickel atom on each of the eight corners of the cell • Simple cubic structure: – 8 corners x 1/8 = 1 atom • Body-centered cubic structure = two atoms per unit cell • Body-centered cubic structure: – (8 corners x 1/8) + 1 body = 2 atoms • Six atoms on the faces of the unit cell = three nickel atoms, for a total of four atoms per unit cell • Face-centered cubic structure: – (8 corners x 1/8) + (6 faces x 1/2) = 4 atoms 11. 7 Structures of Solids by Cara Barskey, Brendan Degnan, Courtney Gregor

Fraction of an atom that occupies a unit cell Position in Unit Cell Center Fraction in Unit Cell 1 Face 1/2 Edge 1/4 Corner 1/8 11. 7 Structures of Solids by Cara Barskey, Brendan Degnan, Courtney Gregor

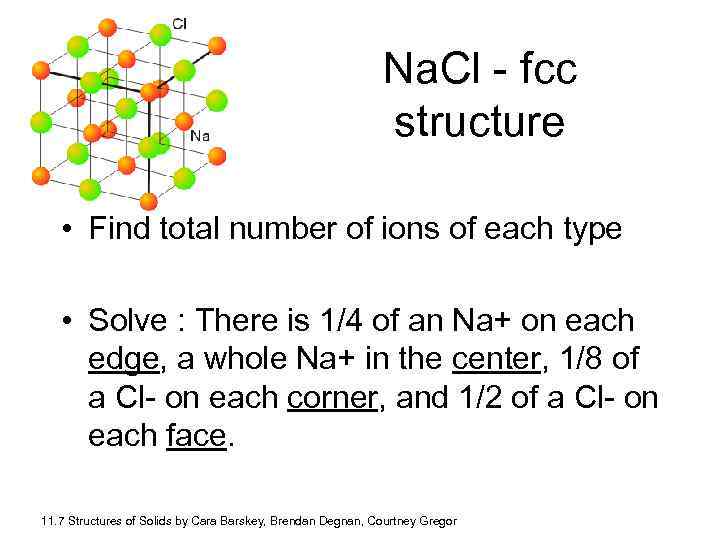
Na. Cl - fcc structure • Find total number of ions of each type • Solve : There is 1/4 of an Na+ on each edge, a whole Na+ in the center, 1/8 of a Cl- on each corner, and 1/2 of a Cl- on each face. 11. 7 Structures of Solids by Cara Barskey, Brendan Degnan, Courtney Gregor

Ionic Bonding Fluorite structure 8: 4 coordination fcc e. g. Ca. F 2, Ba. Cl 2, UO 2, Sr. F 2 Rutile structure 6: 3 coordination Body-centered cubic (bcc) (68% filled) e. g. Ti. O 2, Ge. O 2, Sn. O 2, Ni. F 2 Nickel arsenide structure 6: 6 coordination hcp e. g. Ni. As, Ni. S, Fe. S, Pt. Sn Anti-fluorite structure 4: 8 coordination e. g. Li 2 O, Na 2 Se, K 2 S, Na 2 S You can determine empirical formula for a structure by counting the atoms and partial atoms within the boundary of the unit cell (the box). E. g. in the rutile structure, two of the O ions (green) are fully within the box and there are four half atoms on the faces for a total of 4 O ions. Ti (orange) one ion is completely in the box and there are 8 eighth ions at the corners; this gives a total of 2 Ti ions in the cell. This means the empirical formula is Ti. O 2; the 6: 3 ratio is determined by looking at the number of closest neighbours around each cation and anion. There are many other common forms of ionic structures but it is more important to be able to understand the reason that a salt adopts the particular structure that it does and to be able to predict the type structure a salt might have.

Ionic Bonding The ratio of the radii of the ions in a salt can allow us to predict the type of arrangement that will be adopted. The underlying theory can be attributed to the problem of trying to pack spheres of different sizes together while leaving the least amount of empty space and minimizing the contact between the negatively charged anions. The size of a cation (the smaller sphere) that can fill the hole between close packed anions (the larger spheres) can be calculated using simple geometry. The ratio of the radii can give a rough estimate of the coordination number of the ions which can then be used to predict the structural arrangement of the salt. E. g. for a 3 -coordinate arrangement where A is at the center of the hole (of radius r+) and B is at the center of the large sphere (of radius r-), one can define the right triangle ABC where the angle CAB must be 60°. Sin(60°) = 0. 866 = BC/AB = r-/(r++r-) 0. 866 (r++r-) = r- A C B 0. 866 r+ + 0. 866 r- = r- 0. 866 r+ = r- - 0. 866 r- 0. 866 r+ = (1 - 0. 866) r- = (0. 134) r- So: r+/r- = 0. 134/0. 866 = 0. 155 This means that the smallest cation that will fill in the hole must have a radius that is at least 15. 5% of the radii of the anions. Coordination number 2 3 4 6 8 r+/r- < 0. 155 0. 225 0. 414 0. 732 > 0. 732 structure “covalent” Zn. S Na. Cl Cs. Cl

Coordination number • Each sphere 12 equidistant neighbors • Coordination number = 12 – Number of particles immediately surrounding a particle in the crystal structure • Body-centered has coordination number of 8 • Simple cubic-centered has coordination number of 6 • Unequal-sized spheres: large particles take closepacked arrangements, small particles occupy cavities between larger spheres 11. 7 Structures of Solids by Cara Barskey, Brendan Degnan, Courtney Gregor

Elements and packing • Elemental Cu and Ni each uses fcc packing and both have very similar lattice parameters (e. g. internuclear distances). • If we heat the two elements to melting and then mix together and cool slowly, the fcc packing is retained, but with a random placement of the two elements. • Known as a solid solution ≈ alloy.

Elements and packing • Elemental Cu and Au each uses fcc packing but have very different lattice parameters (Au >> Cu). • Upon reaction (melt and cool) yields a specifically ordered arrangement = an intermetallic compound, which may not conform to oxidation state rules.

Ionic Bonding lattice A CN stoich A/n Cs. Cl 1. 763 (8, 8) AB 0. 882 Na. Cl 1. 748 (6, 6) AB 0. 874 Zinc blende 1. 638 (4, 4) AB 0. 819 wurtzite 1. 641 (4, 4) AB 0. 821 fluorite 2. 519 (8, 4) AB 2 0. 840 rutile 2. 408 (6, 3) AB 2 0. 803 Cd. I 2 2. 355 (6, 3) AB 2 0. 785 Al 2 O 3 4. 172 (6, 4) A 2 B 3 0. 834

Binary Compounds (MX) Which elements do we need to be concerned about? ignore noble gases; no known extended structures. ignore radioactive elements. this leaves about 80 elements of possible interest. mathematically, this results in ~3, 160 possible binary elemental combinations (not taking into account various stoichiometries, AB 2, A 2. 3 B 3, etcetera). 90% of known binary compounds have simple stoichiometries: MX, MX 2, MX 3, M 3 X 5, etcetera. For MX there are 20 common structure types (we’ll look at 3). For MX 2 there are 26 common structure types (we’ll look at 2). Each of these structural types can be thought of as starting from single element packing lattices.

Most Common MX Structures Na. Cl structure Na+ in fcc lattice Cl- in Oh “holes” Cs. Cl structure Cl- in simple cubic lattice Cs+ in cubic “hole” Zinc blende (Zn. S) structure S-2 in fcc lattice Zn+2 in alternating Td “holes”

Most Common MX 2 Structures Fluorite (Ca. F 2) structure Ca+2 in fcc lattice F- in all Td “holes” Rutile (Ti. O 2) structure Ti+2 in body centered cubic lattice Oxygens in lower symmetry array.