Инженерная и компьютерная графика Курс лекций Лекция

Инженерная и компьютерная графика Курс лекций Лекция № 2.

Содержание лекции № 2. 1. 1. Прямая линия. Способы задания прямой линии. 1. 2. Взаимное расположение точки и прямой. 1. 3. Взаимное расположение прямых.

1. 1. Прямая линия Способы задания прямой линии Прямая линия - одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, вдоль которой расстояние между двумя точками является кратчайшим. Прямая линия - алгебраическая линия первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением 1 - ой степени (линейное уравнение). Общее уравнение прямой (полное): Ах+Ву+С=0, где А, В и С - любые постоянные, причем А и В одновременно не равны нулю. Если один из коэффициентов равен нулю, уравнение называется неполным. Для определения положения прямой в пространстве существуют следующие методы: 1. Двумя точками (А и В). 2. Двумя плоскостями ( . 3. Двумя проекциями. 4. Точкой и углами наклона к плоскостям

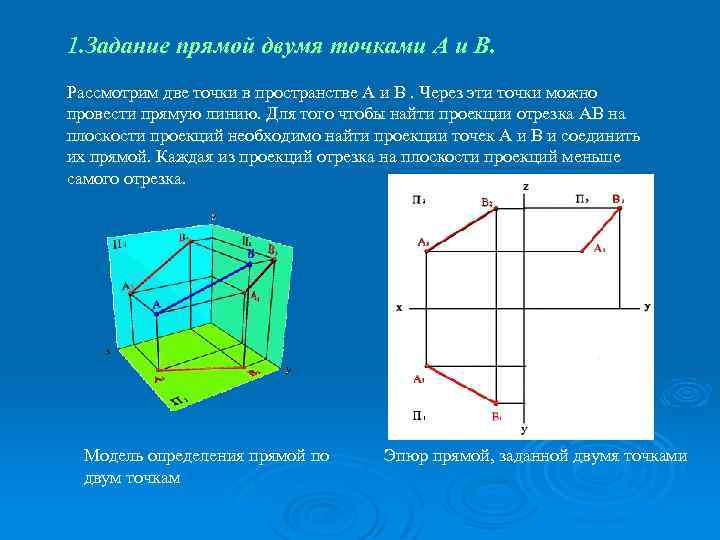1. Задание прямой двумя точками А и В. Рассмотрим две точки в пространстве А и В. Через эти точки можно провести прямую линию. Для того чтобы найти проекции отрезка АВ на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка. Модель определения прямой по двум точкам Эпюр прямой, заданной двумя точками

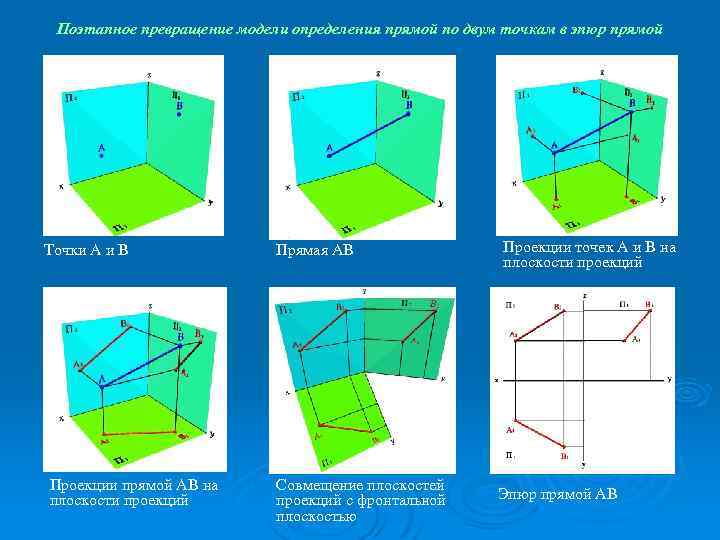Поэтапное превращение модели определения прямой по двум точкам в эпюр прямой Точки А и В Проекции прямой АВ на плоскости проекций Прямая АВ Совмещение плоскостей проекций с фронтальной плоскостью Проекции точек А и В на плоскости проекций Эпюр прямой АВ

2. Задание прямой двумя плоскостями ( . Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии (этот способ подробно рассматривается в курсе элементарной геометрии). 3. Задание прямой двумя проекциями. Пусть в плоскостях П 1 и П 2 даны проекции прямых заданных отрезками А 1 В 1 и 2 2. Проведем через эти прямые плоскости и перпендикулярные плоскостям проекций. В том случае если эти плоскости непараллельные, линией их пересечения будет прямая заданная отрезком АВ , проекциями которой являются отрезки А 1 В 1 и А 2 В 2. Плоскости и могут слиться в одну плоскость , если, например, проекции А 1 В 1 и А 2 В 2 перпендикулярны оси x и пересекают ее в одной точке. Прямая линия в этом случае будет однозначно определена своими проекциями, если на каждой из них обозначить две какие-либо точки. Если же обозначений не делать, то за искомую прямую можно принять любую прямую, лежащую в этой плоскости при условии, что она непараллельная ни одной из плоскостей проекций. Точка К, в данном случае - точка пересечения прямой с плоскостью П 2.

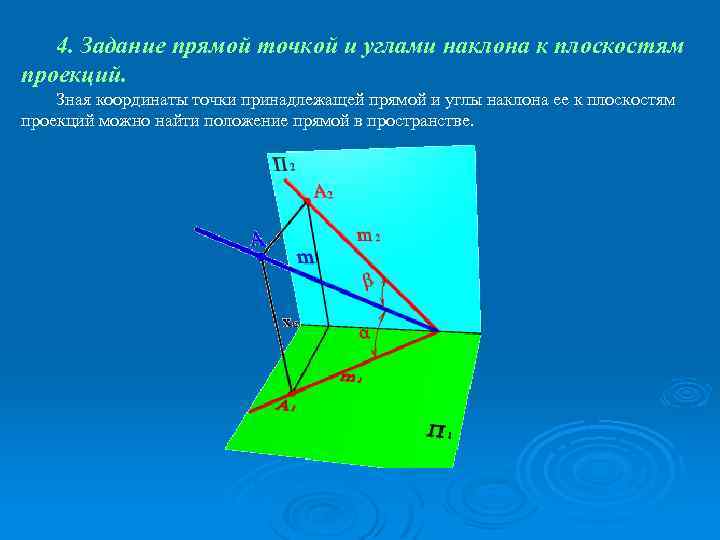4. Задание прямой точкой и углами наклона к плоскостям проекций. Зная координаты точки принадлежащей прямой и углы наклона ее к плоскостям проекций можно найти положение прямой в пространстве.

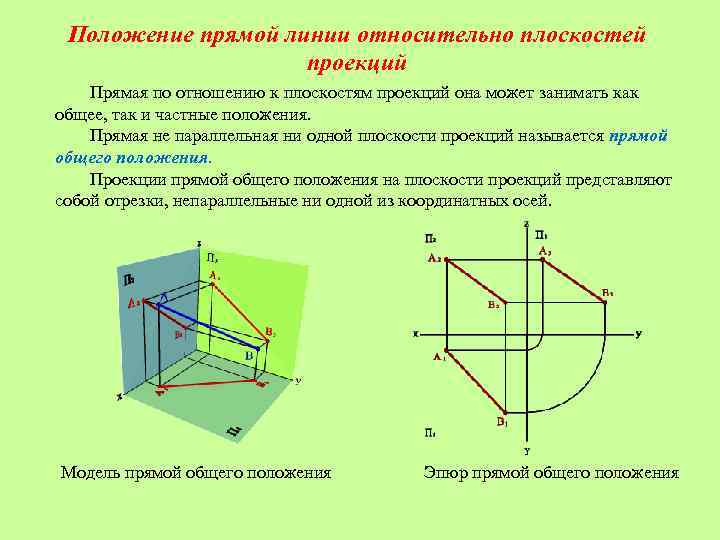Положение прямой линии относительно плоскостей проекций Прямая по отношению к плоскостям проекций она может занимать как общее, так и частные положения. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения. Проекции прямой общего положения на плоскости проекций представляют собой отрезки, непараллельные ни одной из координатных осей. Модель прямой общего положения Эпюр прямой общего положения

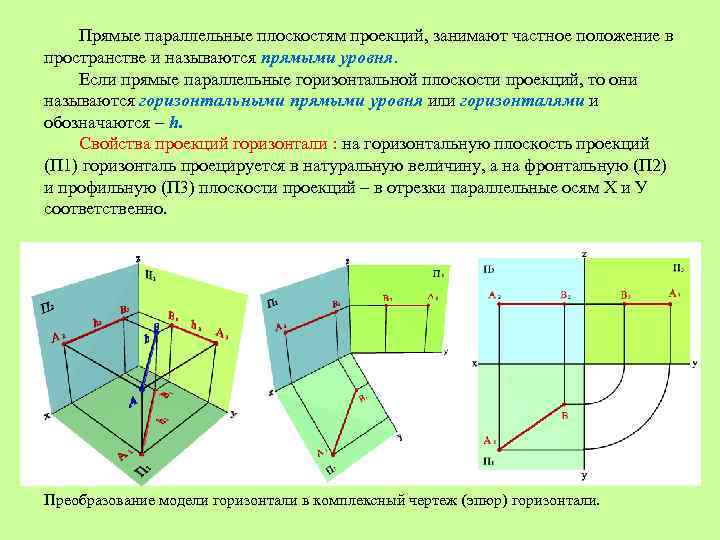Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. Если прямые параллельные горизонтальной плоскости проекций, то они называются горизонтальными прямыми уровня или горизонталями и обозначаются – h. Свойства проекций горизонтали : на горизонтальную плоскость проекций (П 1) горизонталь проецируется в натуральную величину, а на фронтальную (П 2) и профильную (П 3) плоскости проекций – в отрезки параллельные осям Х и У соответственно. Преобразование модели горизонтали в комплексный чертеж (эпюр) горизонтали.

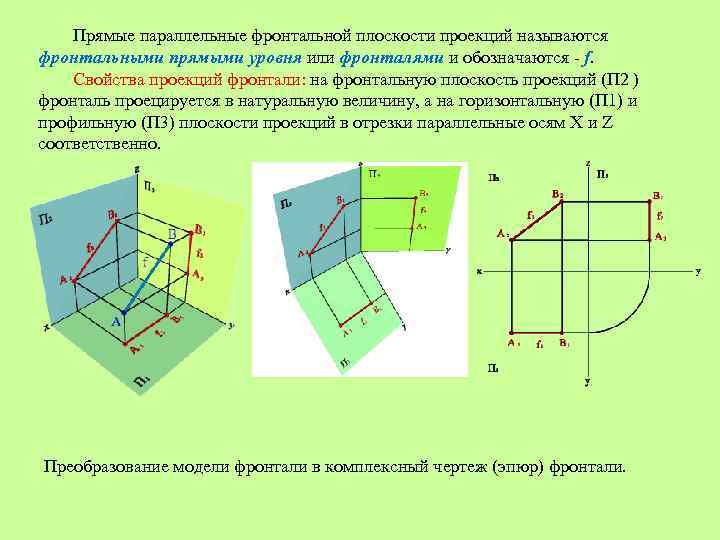Прямые параллельные фронтальной плоскости проекций называются фронтальными прямыми уровня или фронталями и обозначаются - f. Свойства проекций фронтали: на фронтальную плоскость проекций (П 2 ) фронталь проецируется в натуральную величину, а на горизонтальную (П 1) и профильную (П 3) плоскости проекций в отрезки параллельные осям Х и Z соответственно. Преобразование модели фронтали в комплексный чертеж (эпюр) фронтали.

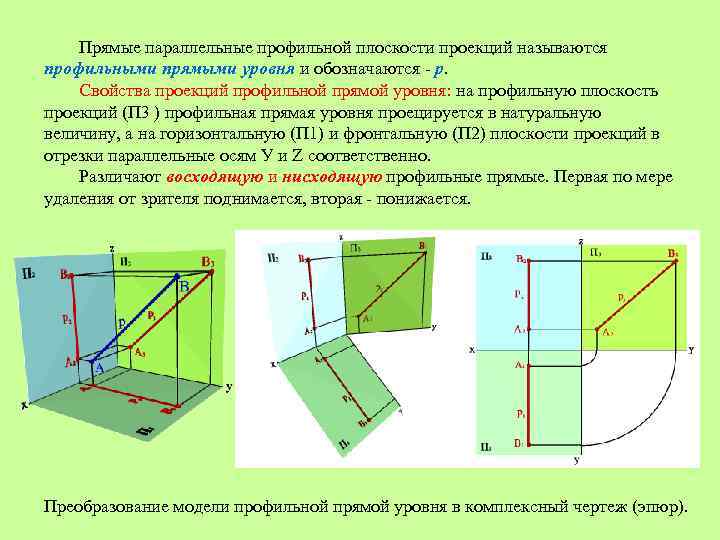Прямые параллельные профильной плоскости проекций называются профильными прямыми уровня и обозначаются - р. Свойства проекций профильной прямой уровня: на профильную плоскость проекций (П 3 ) профильная прямая уровня проецируется в натуральную величину, а на горизонтальную (П 1) и фронтальную (П 2) плоскости проекций в отрезки параллельные осям У и Z соответственно. Различают восходящую и нисходящую профильные прямые. Первая по мере удаления от зрителя поднимается, вторая - понижается. Преобразование модели профильной прямой уровня в комплексный чертеж (эпюр).

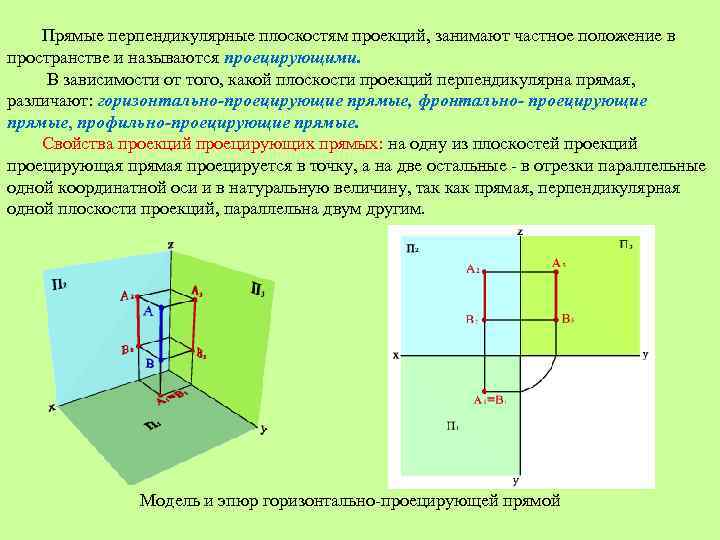Прямые перпендикулярные плоскостям проекций, занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна прямая, различают: горизонтально-проецирующие прямые, фронтально- проецирующие прямые, профильно-проецирующие прямые. Свойства проекций проецирующих прямых: на одну из плоскостей проекций проецирующая прямая проецируется в точку, а на две остальные - в отрезки параллельные одной координатной оси и в натуральную величину, так как прямая, перпендикулярная одной плоскости проекций, параллельна двум другим. Модель и эпюр горизонтально-проецирующей прямой

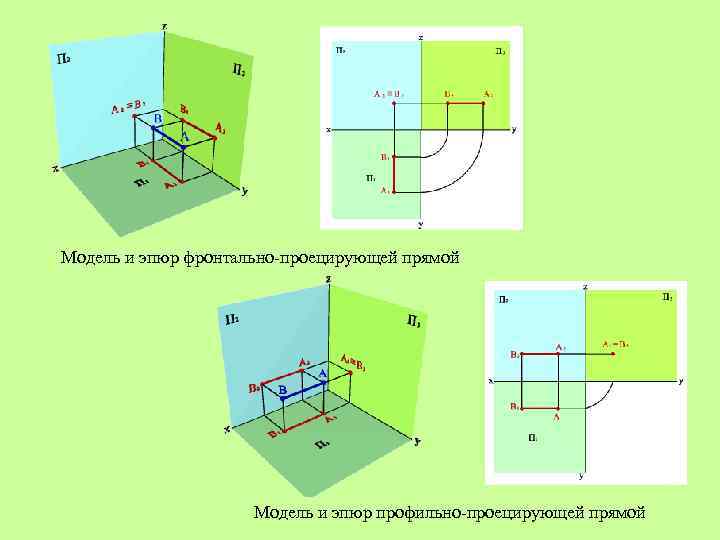Модель и эпюр фронтально-проецирующей прямой Модель и эпюр профильно-проецирующей прямой

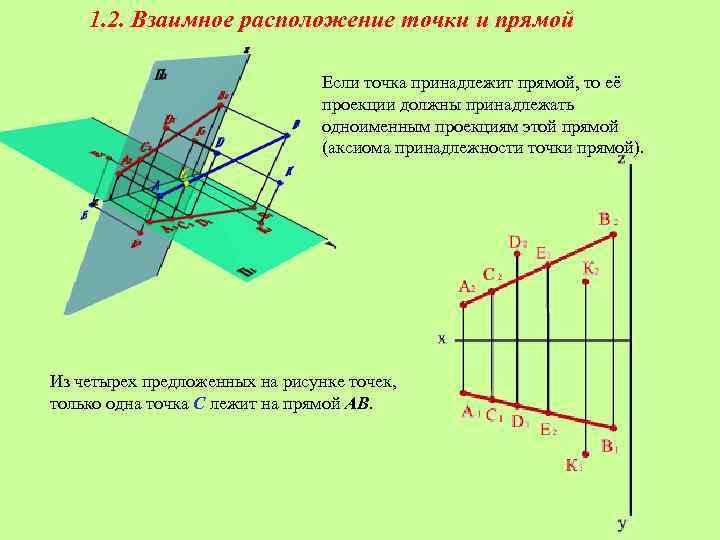1. 2. Взаимное расположение точки и прямой Если точка принадлежит прямой, то её проекции должны принадлежать одноименным проекциям этой прямой (аксиома принадлежности точки прямой). Из четырех предложенных на рисунке точек, только одна точка С лежит на прямой АВ.

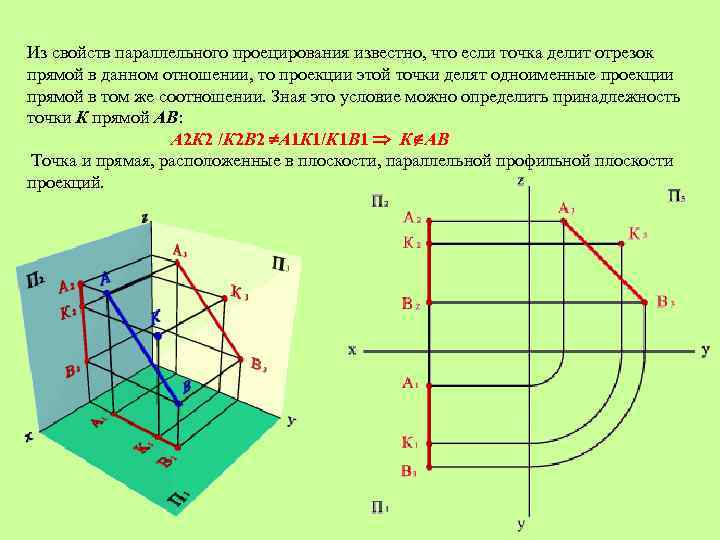Из свойств параллельного проецирования известно, что если точка делит отрезок прямой в данном отношении, то проекции этой точки делят одноименные проекции прямой в том же соотношении. Зная это условие можно определить принадлежность точки К прямой АВ: А 2 К 2 /К 2 В 2 А 1 К 1/К 1 В 1 К АВ Точка и прямая, расположенные в плоскости, параллельной профильной плоскости проекций.

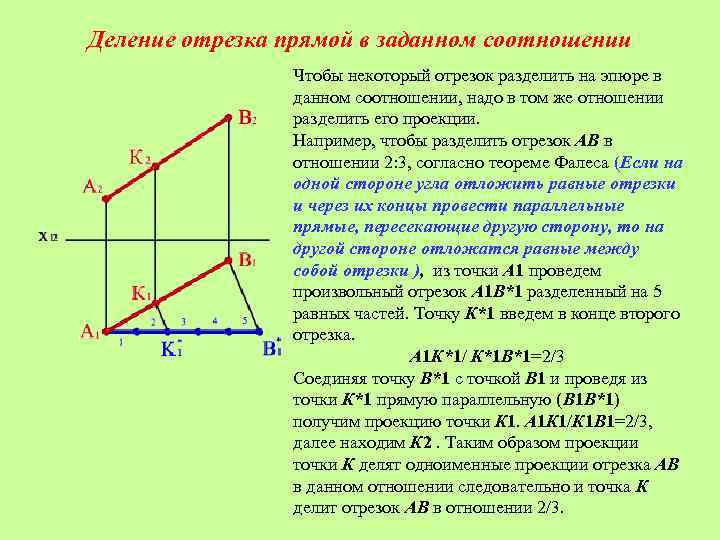Деление отрезка прямой в заданном соотношении Чтобы некоторый отрезок разделить на эпюре в данном соотношении, надо в том же отношении разделить его проекции. Например, чтобы разделить отрезок АВ в отношении 2: 3, согласно теореме Фалеса (Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие другую сторону, то на другой стороне отложатся равные между собой отрезки ), из точки А 1 проведем произвольный отрезок А 1 В*1 разделенный на 5 равных частей. Точку К*1 введем в конце второго отрезка. А 1 К*1/ К*1 В*1=2/3 Соединяя точку В*1 с точкой В 1 и проведя из точки К*1 прямую параллельную (В 1 В*1) получим проекцию точки К 1. А 1 К 1/К 1 В 1=2/3, далее находим К 2. Таким образом проекции точки К делят одноименные проекции отрезка АВ в данном отношении следовательно и точка К делит отрезок АВ в отношении 2/3.

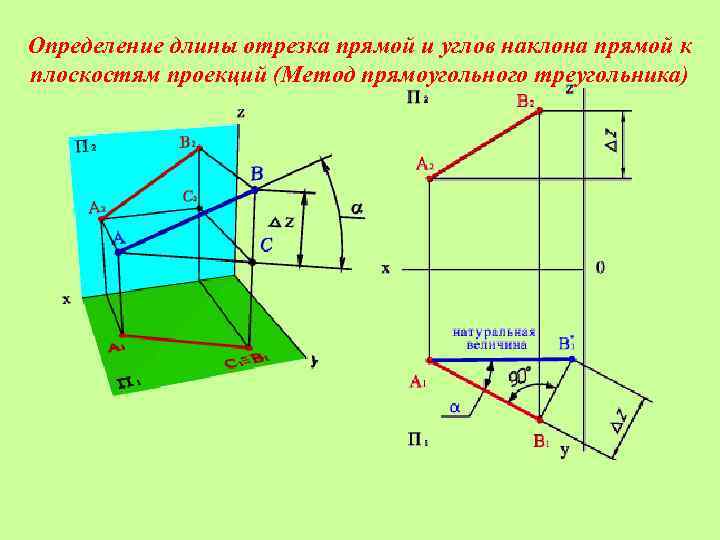Определение длины отрезка прямой и углов наклона прямой к плоскостям проекций (Метод прямоугольного треугольника)

1. 3 Взаимное расположение прямых Прямые линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися. 1. Параллельные прямые линии. Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек. Проекции параллельных прямых на любую плоскость (не перпендикулярную данным прямым) - параллельны. Если AB CD то A 1 B 1 C 1 D 1; A 2 B 2 C 2 D 2; A 3 B 3 C 3 D 3. В общем случае справедливо и обратное утверждение.

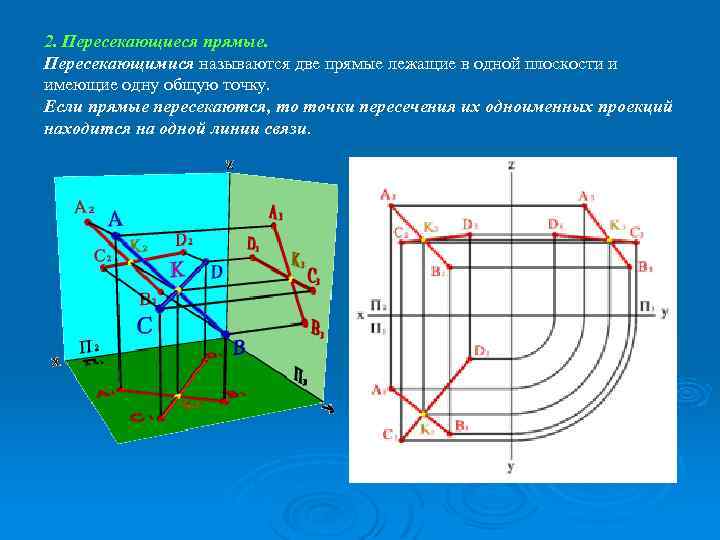2. Пересекающиеся прямые. Пересекающимися называются две прямые лежащие в одной плоскости и имеющие одну общую точку. Если прямые пересекаются, то точки пересечения их одноименных проекций находится на одной линии связи.

3. Скрещивающиеся прямые Скрещивающимися называются две прямые не лежащие в одной плоскости. Если прямые не пересекаются и не параллельны между собой, то точка пересечения их одноименных проекций не лежит на одной линии связи. Точке пересечения фронтальных проекций прямых соответствуют две точки А и В, из которых одна принадлежит прямой а, другая в. Их фронтальные проекции совпадают лишь потому, что в пространстве обе точки А и В находятся на общем перпендикуляре к фронтальной плоскости проекций. Горизонтальная проекция этого перпендикуляра, обозначенная стрелкой, позволяет установить, какая из двух точек ближе к наблюдателю. На предложенном примере ближе точка В, лежащая на прямой а, следовательно, прямая а проходит в этом месте ближе прямой в и фронтальная проекция точки В закрывает проекцию точки А. (Для точек С и D решение аналогично). Этот способ определения видимости по конкурирующим точкам. В данном случае точки А и В- фронтально конкурирующие, а С и D -горизонтально конкурирующие.

Спасибо за внимание! Следующая лекция будет еще интересней!